基于灰色模型的关键链缓冲监控优化研究

何雨行

(上海交通大学电子信息与电气工程学院，上海 200030)

0 引言

敏捷开发(Agile Development)以其需求动态响应、持续集成、增量交付、快速迭代等特点，逐渐成为软件项目主流开发模式。然而，对于一些技术复杂度高、不确定性风险大的活动，敏捷开发经常会出现进度约束困难、进度偏差发现较迟的问题，从而导致项目进度延期。在敏捷开发中引入关键链法(Critical Chain Method，CCM)，可以对活动形成有效的约束，提高活动的按时完工概率。然而，敏捷开发迭代周期短，可设置的缓冲大小受限，因此，通过对关键链缓冲设置优化难以取得良好效果。此外，敏捷开发对进度风险更为敏感，传统关键链监控方法大多是通过调节缓冲区触发点位置来被动监控预警，预警时间较为滞后，难以有充足的反应时间采取行动，仍会导致项目进度延期。

基于此，本文结合敏捷开发的特点，提出主动利用活动状态预测活动完工时间，而非被动地通过缓冲区触发点阈值的设置来调整缓冲监控告警频率，提升了感知进度风险的效率，为采取行动提供了充足的反应时间。根据当前的活动进度状态及变化趋势两个维度的变量，通过卡尔曼滤波消除观测波动带来的噪声，结合灰色模型准确地对活动完工时间与缓冲消耗情况进行评估，并采取相应的管理措施，以保证活动按期完工。

1 文献综述

关键链缓冲监控是关键链研究的核心问题之一，国内外众多专家学者都对其进行了广泛而深入的研究。Goldratt[1]提出将缓冲区等分为红色、黄色、绿色三部分进行管理，即静态三分法。Leach[2]提出缓冲监控的触发点位置可以随着项目进度变化而变化的相对监控法，防止缓冲监控点较低而发出错误的预警。别黎等[3]在静态三分法的基础上，提出在项目执行过程中动态改变两个触发点的缓冲监控策略。在此基础上，别黎等[4]提出基于活动敏感性的动态缓冲监控方法，设置监控活动敏感性的监控阈值。张俊光等[5]在缓冲监控中引入活动缓冲消耗位置和速率信息，并在此基础上对活动缓冲消耗进行预测，实时调整两个触发点的位置。张俊光等[6]提出基于项目资源细分的关键链进度监控方法，该方法根据不同的资源特性确定缓冲预警状态值。另外，张俊光等[7]基于马尔科夫链提出一种周期性项目缓冲监控模型，该模型计算活动状态转移的可能性，以便于采取应急处理措施。马萍等[8]考虑活动的不确定性影响，采用层次分析法和熵权法的主客观组合赋权法，结合灰色关联分析对缓冲大小设置进行改进。胡雪君等[9]提出采用统计过程控制进行两阶段缓冲消耗监控，建立活动层面工期波动的缓冲控制图，当活动缓冲消耗超出监控阈值时触发预警，并采取相应的应对措施。王乾坤等[10]提出采用BIM系统的关键链项目管理，利用自动化软件技术实现对项目的统筹管理。

综上所述，当前缓冲监控研究主要在静态三分法的基础上，结合项目特性，对缓冲监控阈值进行调节，减少活动进度风险。然而，现有方法仍停留在利用缓冲区预警阈值的设置被动消除活动进度风险的层面，并且尽量少地触发缓冲预警以避免管理成本的增加。但是，这样的结果会导致发现活动进度风险的时间点较晚，往往留给采取行动的时间不多，从而未能对活动风险实现良好的控制效果。本文利用活动执行时期的进度状态来预测活动完成时的缓冲消耗，可以在早期发现潜在的活动进度延期风险，并及时采取纠正措施。

2 基于灰色模型的关键链缓冲监控

2.1 活动进度状态及变化率

在关键链进度管理中，活动进度可以定义为已完成工作量与工作总量的比值，而进度变化率可以由相邻两次监控点的平均进度变化率近似代替。公式如下

(1)

式中，δi(t)与νi(t)分别为活动i在t时刻完工进度和进度变化率；ni(t)为完成的工作包数量；N为工作包总数；Δt为活动的监控周期。

2.2 卡尔曼滤波活动最优状态估计

定义活动i在t时刻状态空间向量

(2)

式中，xi(t)为活动i在t时刻状态空间向量；δi(t)为活动进度；νi(t)为进度变化率。

利用卡尔曼滤波算法对活动i在t+1时刻状态空间向量进行最优状态预测，公式如下

(3)

(4)

(5)

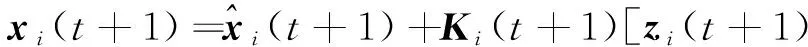
(6)

(7)

2.3 灰色模型缓冲消耗预测

(8)

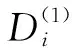
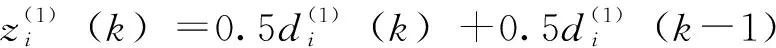
(9)

建立模型灰微分方程，公式如下

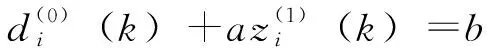
(10)

式中，参数a为灰色发展系数；参数b是灰色作用量。

相应的白化微分方程如下

(11)

(12)

(13)

求解白化微分方程得到预测方程如下

(14)

差分计算还原原始序列预测值，公式如下

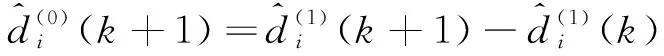
(15)

定义活动i在t时刻进度风险系数ηi(t)

(16)

定义活动i的临界系数θi

(17)

式中，Bi为分散式缓冲大小；Ti为计划工期。

将ηi(t)与θi进行比较，可以得到如下结论：

(1)当ηi(t)≤1时，反映当前活动进展顺利，将在计划的活动工期内完成。这种情况下，不仅活动i全部的缓冲区可以累积并作为额外缓冲分配给其余的活动，而且还有部分的计划活动工期可以被释放出来。因此，不需要花费过多精力进行干预，只需要保持定期活动状态监控即可。

(2)当1<ηi(t)≤θi时，反映当前活动相比计划出现延迟，但是还可以在缓冲时间内完成。此时需要分析可能造成活动进度迟缓的原因，并加强对于活动状态的监控，观察后续的状态是否有改善的趋势。

(3)当ηi(t)>θi时，反映当前活动最终将会耗尽缓冲区，造成进度延期，并且可能对同一链路上其他活动造成影响，降低其他活动的安全时间裕量。此时应该及时采取措施干预，找出导致活动进展缓慢的根本原因，分析和评估可能带来的影响，利用赶工或增加资源等方式弥补进度滞后，降低进度延期风险。

3 案例验证

3.1 案例分析

某通信软件产品采用敏捷方法进行开发迭代。在一次迭代中主要增加三个功能模块，项目周期为60d，包括16项活动。项目采用关键链法进行进度管理，项目缓冲15d，采用根方差法计算活动缓冲大小并采用分散式缓冲管理方式。活动基本信息见表1。

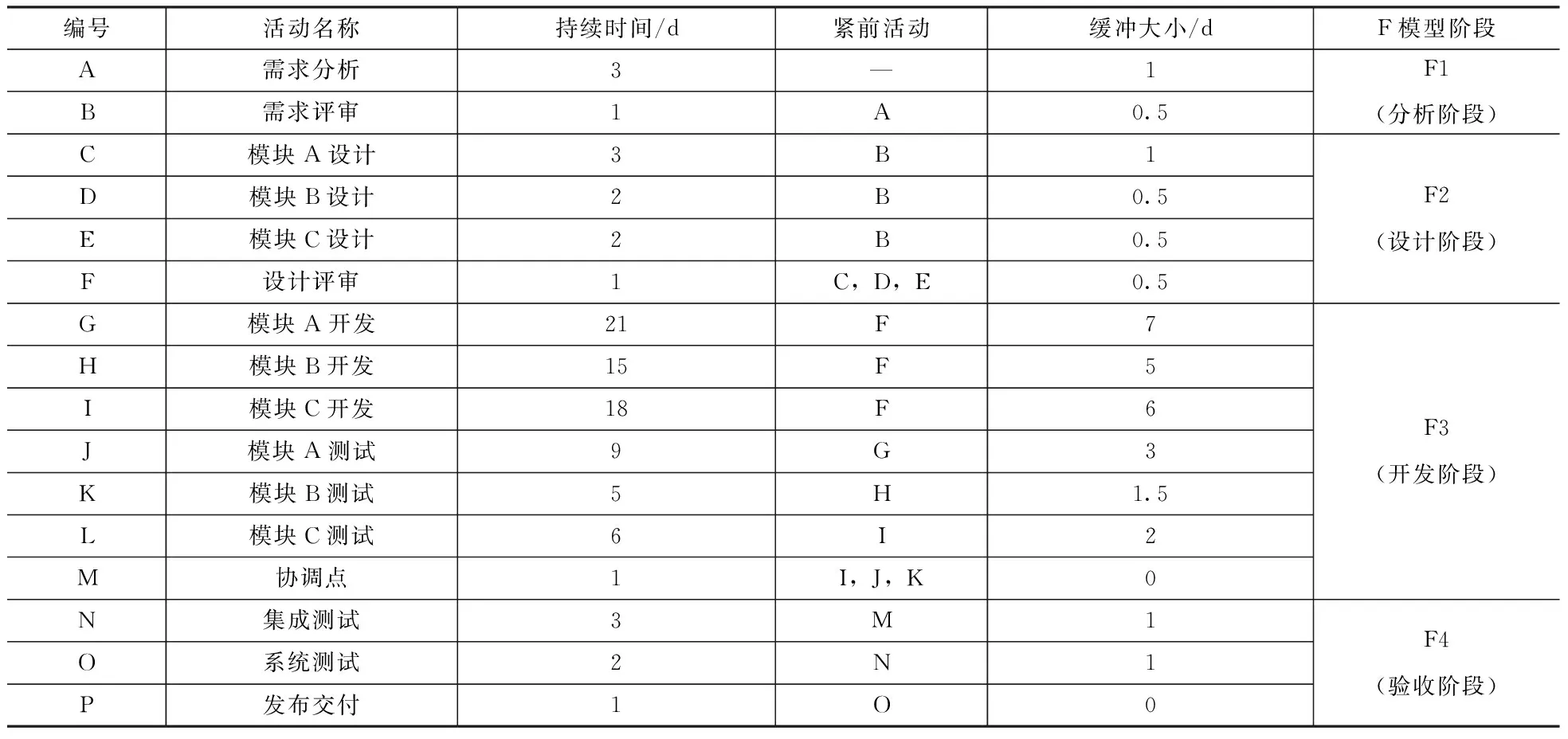
表1 活动基本信息

根据活动基本信息可以绘制出关键链网络图，如图1所示。其中，空心方块代表具体的每项活动，实心方块代表项目缓冲或接驳缓冲，虚线方块代表将缓冲分散到每项活动上，使每项活动都有各自的缓冲控制基准，以便后续的缓冲控制管理。

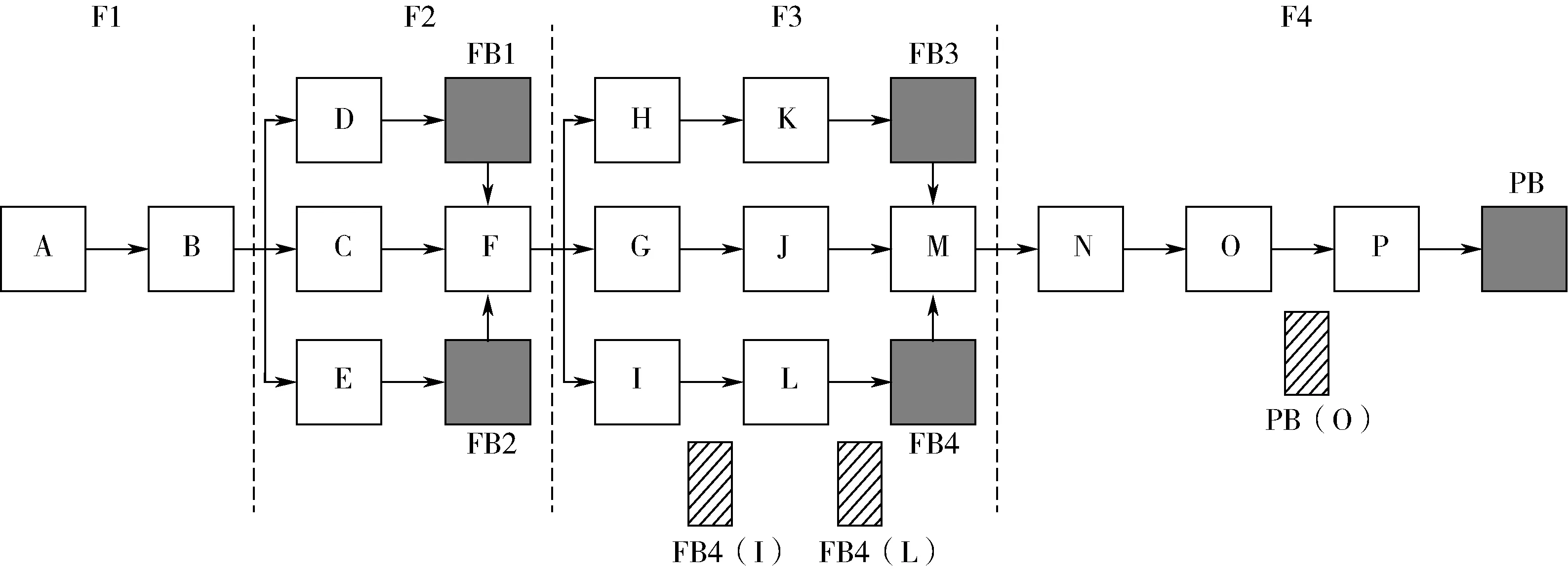
图1 关键链网络图注：FB为接驳缓冲，PB为项目缓冲。

对不同风险水平的各个活动进度状态及变化趋势进行模拟，可以得到活动预期完工进度曲线。通过调节卡尔曼滤波状态方程的参数，可以对完工进度滤波的效果进行调节，以得到真实的活动进度状态估计。活动H进度卡尔曼滤波效果对比如图2所示。

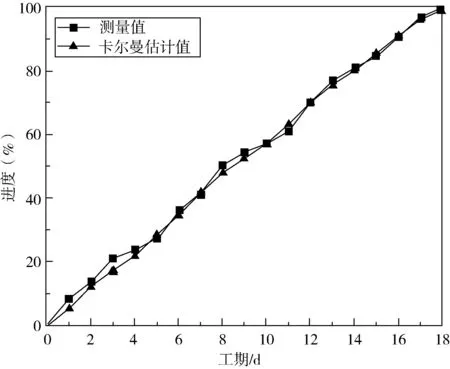
图2 活动H进度卡尔曼滤波效果对比

基于灰色模型的关键链缓冲监控方法流程图如图3所示。具体执行步骤如下：

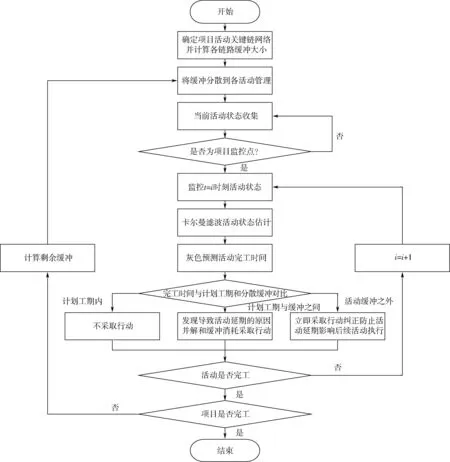
图3 基于灰色模型关键链缓冲监控步骤流程图

(1)确定项目活动关键链网络。

(2)确定各个链路上的缓冲区大小并分散到各个活动中。

(3)利用卡尔曼滤波对当前活动状态进行最优状态估计，消除观测产生的活动进度状态误差，得到真实的活动状态。

(4)根据当前活动的执行状态，采用灰色模型对活动完工工期进行预测。

(5)将预测的完工工期与计划工期和活动分散缓冲进行对比。如果预测的完工工期小于或等于计划工期，说明当前的活动进度状态良好，不需要采取行动纠正；如果预测的完工工期大于计划工期，但是未超出活动最大分散缓冲范围，说明当前的活动进度状态出现一定程度滞后，但是仍然在预先分配的缓冲范围内，此时需要及时查明导致活动进度迟缓的原因；如果预测的完工工期超出活动最大分散缓冲范围，说明当前的活动进度产生了严重的滞后，可能会对后续活动产生影响，需要尽快采取行动纠正，必要时可以采取增加资源、赶工等措施，防止项目进一步延期。

(6)对下一时刻的活动状态进行观测，重复步骤(3)～步骤(5)，直到活动完工。

(7)计算活动的剩余缓冲并调整后续活动的分散缓冲。如果活动完工之后缓冲仍有剩余，则可以将剩余缓冲累积到总缓冲中，增加后续活动的缓冲裕量；如果活动完工之后缓冲超量消耗，则应该将超量消耗从总缓冲中减去，加强对于后续各活动的缓冲监控预警。

(8)对后续紧邻活动进行执行，重复步骤(2)～步骤(7)，直到项目完成。

3.2 仿真验证

利用MATLAB对本文方法进行仿真，采用蒙特卡洛模拟，重复进行10 000次实验，对案例中关键链上的各项活动完工时间单独进行统计分析。对比本文方法与静态三分法、相对监控法、动态监控法对于缓冲监控的效果，项目活动完工时间落在各区域的频数统计分布见表2。

表2 项目活动完工时间落在各区域的频数统计分布

从表2中数据可以得出，本文方法相对于其他三种缓冲监控方法而言对于风险较大、不确定程度较高的活动有着显著的效果。例如，活动G、J大部分落在计划工期内，小部分会消耗缓冲区，只有极少的会落在缓冲区外。对于风险较小、不确定程度较低的活动，其持续时间与缓冲区都较小，缓冲监控效果一般。例如，活动A、B、C落在缓冲区内的次数明显增多，并且对于落在缓冲区外的活动，缺少采取纠正措施的时间，此时缓冲监控效果一般。

利用MATLAB对案例中项目整体进行仿真，采用蒙特卡洛模拟，重复进行10 000次实验，对比在不同的缓冲监控方法下项目完工情况。不同缓冲监控方法项目完工时间分布如图4所示。

图4 不同缓冲监控方法项目完工时间分布

从图4可以看出，各种缓冲监控方法完工时间分布大致服从正态分布。将本文方法与静态三分法、相对监控法、动态监控法进行对比，结合实验结果可以得到如下结论：

(1)采用本文方法的项目活动完工模拟中，完工工期均值为44d，最大完工时间为52d，最小完工时间为35d，其中大部分落在计划工期之内，小部分落在项目缓冲之内，均没有超出项目缓冲。表明本文方法的缓冲监控效果较好，完工时间消耗更短，落在计划工期内的完工可能性也较大。本文方法会在项目执行过程中不断地监控活动当前的进度状态及变化趋势，对完工时间及缓冲消耗进行动态预测，因此可以在活动进度产生偏离的早期就及时发现，并采取及时的纠正措施。

(2)采用静态三分法的项目活动完工模拟中，完工工期均值为58d，最大完工时间为63d，最小完工时间为53d，其中均没有落在计划工期内，大部分落在项目缓冲之内，小部分落在项目缓冲之外。由此可以看出静态三分法在应对缓冲设置受限、活动不确定性和风险较大的情况时的缓冲监控效果欠佳。

(3)采用相对监控法的项目活动完工模拟中，完工工期的均值为58d，最大完工时间为68d，最小完工时间为54d，其中均没有落在计划工期内，大部分落在项目缓冲之内，小部分落在项目缓冲之外。相对监控法为了减少缓冲告警次数，在活动执行过程中根据活动进度相对地调整缓冲区的大小，但与此同时也导致对于活动的进度偏离缺乏敏感性，极大地提升了项目延期概率。

(4)采用动态监控法的项目活动完工模拟中，完工工期的均值为58d，最大完工时间65d，最小完工时间51d，其中均没有落在计划工期内，大部分落在项目缓冲之内，小部分落在项目缓冲之外。动态监控法在活动执行过程中根据活动进度动态地调整缓冲监控预警阈值，使得缓冲预警产生的误告警频次下降，但与此同时也导致对于活动的进度偏离感知能力下降，增大了项目延期概率。

4 结语

本文提出了一种基于灰色模型的关键链缓冲监控优化方法。该方法考虑了活动进度状态及变化趋势对于项目工期的影响，采用卡尔曼滤波计算出当前活动状态的最优估计，消除了观测值波动对于预测结果的影响，并利用灰色模型对活动完工时间进行预测，可以尽早发现活动中潜在的进度风险，及时采取行动控制活动进度。相对于传统静态三分法、相对监控法和动态监控法，本文方法对于技术复杂度大、不确定性风险高的活动有着更好的控制效果，避免在活动进行后期发现进度迟缓后再花费更多的管理成本弥补进度延期。因此，本方法适用于多种类型的项目进度管理，尤其对于敏捷开发项目进度管理有着不错的效果。