借助生活素材生成数学概念

李焕

在初中数学的学习中，学生在认识上有两次质的飞跃。第一次飞跃是代数式的学习，由具体的数到具有普遍意义的式；第二次飞跃是函数的学习，由静止不变的数到运动变化的数。函数这节课的教学就是要带领学生感受生活中的变化，体会变量与变量间对应的关系，经历由生活情境归纳函数概念的过程，体会由特殊到一般、由具体到抽象的思维过程。

对于函数概念，笔者认为可以从以下5个方面进行教学。

一、背景意义高位引领

很多教师在展示了常量与变量后就开始引入具体例子，让学生感受变量间的关系，这种做法显得操之过急。从学生的角度来看，他们一定会产生一个疑问：“为什么要学习函数？”如果不给学生解释清楚这个问题，那么本节课不可避免地会成为灌输式教学。数学是一门讲道理的学科，凡事要问个为什么。教师如果只交代“数学来源于生活，生活中有变量，所以我们要学习函数，研究变量间的关系”，这便属于无效教学，没有交代清楚学习函数的背景和意义。

对此，笔者从以下几个角度来引导学生。例如，“我们生活在一个变化的世界，潮起潮落、云卷云舒、沧海桑田，变化在我们身边无处不在，这个世界中唯一不变的就是变化。我学习数学，我想要从数学的角度去研究身边的这些变化。”“如果我能了解变化背后的规律，那么我就能预测未来发展的趋势，也就是说我具有了未卜先知的能力。古人用二十四节气来预测一年中气候的变化；现在天气预报可以预测未来几天天气的情况；导航利用大数据建模预测城市交通的拥堵情况……这些未卜先知是多么神奇而又美妙。”“一个变化过程中往往有多个变量，而这些变量之间又有着错综复杂的关系。我们刚开始学习，可以从简单的入手，先研究两个变量之间的关系。”这些角度分别说明了学习函数的背景、意义以及学习策略，在交代了以上内容以后，再进入函数概念的生成过程，学生便会带着强烈的好奇心主动投入学习。

二、三个素材全面覆盖

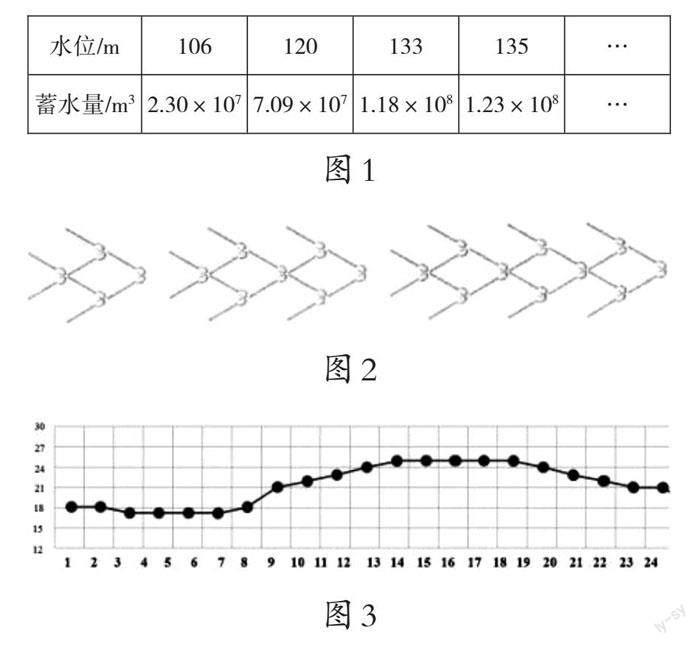
为了能自然地生成函数的概念，教师可以给学生展示3个比较特别的生活中的素材，如下页图1—图3。

图1为某水库水位的高低与相应蓄水量关系的表格。由表格可以看出，随着水位的升高，蓄水量增大；随着水位的降低，蓄水量减少；当水位确定时，蓄水量也随之确定。图2中，用火柴棒搭建小鱼，小鱼的条数n与火柴棒的根数S之间的关系可以很清楚地表示出来，隨着n的增大，可以得到表达式S=6n+2。图3为常州市某天24小时内气温变化的图像。这3个素材分别对应函数的三种表示方式：表格、表达式、图像。虽然这不是本节课的教学内容，但是教师在选择教学素材时要考虑全面，让学生首次接触函数时就能对函数的表示方式有全面的印象，也为下节课学习函数的表示方法做好知识铺垫。

三、三个层次深度理解

对于以上3个素材，每一个教师都要带领学生从3个层次进行深度理解。以图1为例，第一个层次，“变化”。随着水位升高，蓄水量增大；随着水位降低，蓄水量减少。第二个层次，“确定”。当水位确定时，蓄水量也随着确定。第三个层次，“对应”。当水位取定一个值时，蓄水量也有一个值和它对应。以上3个层次，由具体到抽象，对函数概念的阐释不断加深。要理解函数概念，就要理解对应关系，但是学生如果不能理解变量之间变化与确定的关系，也很难理解对应关系。如图1，教材中，其实编写者早已将变化与确定写在了表格下方，这就需要教师认真研读教材，理解编写者的真实意图。

四、生成概念，再识素材

经历了3个素材、3个层次的深入理解，学生对变量间的关系已经有了一定认识。函数概念在学生头脑中生长，此时，教师要做的就是引导学生用数学语言将自己的认识表述出来。从表面上来看，这3个素材没什么联系，但是如果我们从变化、确定、对应的角度来看，这3个素材竟然是如此惊人的相似。教师可以请学生从变化、确定、对应的角度归纳这3个素材的共同属性。由于函数概念对学生来说是非常抽象的，所以，学生归纳概念时，如果语言表述不到位，教师可以进行适当引导，学生只需要讲出变量间存在对应关系即可。

在得出函数概念后，教师再带领学生从函数的角度认识以上3个素材：对于水位高度的每一个值，蓄水量都有唯一的值与它对应；对于小鱼的每一个值，火柴棒的数量都有唯一的值与它对应；对于时间的每一个值，温度都有唯一的值与它对应。至此，学生对于两个变量之间关系的认识经历了4个层次，分别是变化、确定、对应、函数。相信经历以上学习过程，学生对函数概念能有一个较为深入的理解。

五、渗透历史文化熏陶

恩格斯说：“有了变数，运动进入了数学；有了变数，辩证法进入了数学；有了变数，微分和积分也就立刻成为必要的了。”托马斯称函数概念为近代数学思想之花，可见函数对近代数学发展的影响之大。那么，在函数概念的教学中，如果不给学生讲讲函数的发展历史，对学生来说也是一种遗憾。对于函数的发展史，教师可以从两条线来讲，其一是欧洲的多位知名数学家对函数发展做出的贡献。如莱布尼兹首次使用“function”，伯努利、欧拉、柯西等都给函数下过定义，奥斯瓦尔德维布伦用“集合”和“对应”的概念给出了近代函数的定义等。其二是中国的数学家李善兰和英国人伟烈亚力一起翻译了《代数学》，将函数引入了中国，推动了中国乃至整个东亚近代数学，尤其是微积分的发展。

总而言之，一堂好的概念课教学，一定要解决好怎样逐步生成概念这个问题。教师要选择好的生活素材，调动和引导学生经历独立思考、归纳总结的过程，从而自然地生成概念。

（作者单位：江苏省常州市武进区淹城初级中学）