考试命题中模型简化的科学性研究

李睿 李越 陈志华

摘   要： 真实问题情境在命制物理试题中是考查或培养学生模型建构、科学推理等科学思维能力的良好素材。为了适配相应的学业水平，部分试题会理想化真实情境，简化从中构建的物理模型。文章分析2022年福建省中考物理试卷的压轴计算题，讨论物理简化模型的科学性和命题的严谨性，提出真实问题情境中物理模型科学简化的条件，为情境化试题的命制提供参考，并引发了对教学中重力加速度变化的思考。

关键词：中考物理题；模型简化；真实问题情境；科学思维

义务教育物理课程标准倡导“强调真实问题情境，引导学生不断探索，提高分析问题、解决问题的实践本领和科学思维能力，发展核心素养”的课程理念[ 1 ]。从真实情境问题中构建物理模型，可以引导学生在科学探究过程中学习科学研究方法、养成科学思维习惯[ 2 ]。在实际进行情境设计时，需要抓住主要因素，忽略次要因素，降低模型复杂程度，才能与当前学业水平相符，因此，中考物理试题的题干中，“忽略”“不考虑”“不计”等字眼的出现屡见不鲜。笔者以2022年福建省中考物理试卷的压轴计算题（第31题）为例，分析与讨论在真实情境问题中如何对物理模型进行科学合理的简化，为“双减”背景下真实情境试题的设计提供参考。

1 真题解析与思考

1.1真题再现

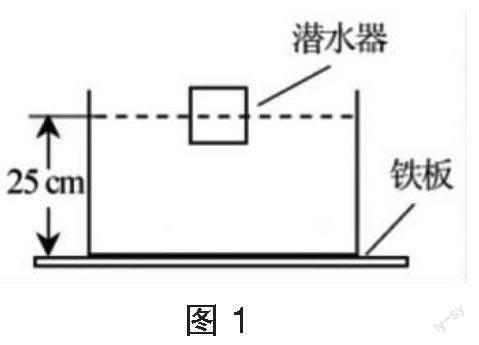
如图1是一款能自动浮沉的潜水玩具，正方体潜水器内装有智能电磁铁，将它放入装有水的圆柱形薄壁容器中，容器放置在水平铁板上，不计容器的重力。潜水器启动后通过传感器测出其底部与铁板间的距离l，自动调节电磁铁电流大小，改变潜水器与铁板间的吸力F的大小。闭合开关前，潜水器处于漂浮状态。闭合开关，潜水器启动后先匀速下沉，完全浸入水中后，变为加速下沉直至容器底部，下沉全过程F随l变化的关系保持不变，水深变化的影响忽略不计。已知潜水器的边长为10 cm，重为5 N，容器的底面积为1000 cm2，水深为25 cm。求：

（1）潜水器漂浮时受到的浮力。

（2）下沉全过程潜水器重力所做的功。

（3）潜水器沉底静止后容器对铁板的压强。

1.2真题解析

该试题在潜水玩具的自动沉浮过程中考查浮力、重力、压强、功等物理概念，以及模型建构和科学推理等科学思维水平。案例鲜活，贴近学生生活。题目的设问逐步递进，梯度合理，有利于学生发挥正常水平，契合中考评价体系“一核、三层、三翼”的要求。

第（1）问主要考查漂浮状态下物体的受力分析和二力平衡条件，难度小。学生通过分析潜水器在漂浮时受到竖直向下的重力和竖直向上的浮力作用，根据平衡条件，即可得到正确答案：漂浮时受到的浮力为F浮=G潜=5 N。

第（2）问主要考查阿基米德原理和重力做功，难度一般。根据阿基米德原理可求得漂浮时潜水器的浸水深度：

其中S1是潜水器的底面积，即S1=100 cm2。下沉全过程中，潜水器下沉距离？驻l等于漂浮时其底面与容器底部的间距，因此，该过程中重力所做的总功为：

WG=G潜Δl=G潜（H0-x0）=1 J②

其中H0是初始水深，即H0=25 cm。

第（3）问有一定的难度，区分度较高，要求学生具备较好的科学推理能力。学生仅知道压强的计算公式是不够的，还要能够分析作用于铁板的压力情况，具体推理过程如下：

首先，压力的来源分析。由于“容器重量不计”，潜水器沉底静止后，作用于铁板上的压力包含水的重力G水、潜水器的重力G潜以及潜水器与铁板之间的吸力F。

其次，重力的计算。根据阿基米德原理分析得到水与潜水器的总重力就等于25 cm深的水的重力，即

G水+G潜=ρ水gS2H0=250 N③

其中S2是容器的底面积，即S2=1000 cm2。

再次，潜水器沉底静止时与铁板间的吸力F0的计算。匀速下沉过程中，潜水器在自身重力G潜、浮力F浮和吸力F的共同作用下处于平衡状态。任意时刻潜水器底部与铁板距离为l，考虑到“水深变化的影响忽略不计”，则根据平衡条件可以求得吸力为

F=F浮-G潜=ρ水gS1（H0-l）-G潜 ④

之后以此规律加速下沉。因此，沉底（l=0）静止时，潜水器与铁板间的吸力为

F0=ρ水gS1H0-G潜=20 N⑤

最后，代入公式求得压强：

1.3  模型简化讨论

题目中通过忽略水深变化来简化模型的做法是否科学？下面分别分析考虑水深变化与忽略水深变化的模型，通过对比两种模型中相关物理量的变化情况来讨论模型简化的严谨性，从中得到真实问题情境下物理模型科学简化的条件。

1.3.1  考虑水深变化的实际模型

由生活中的真实情境可知，潜水器完全浸入水之前，水面会随着潜水器的下沉而上升，使得水深发生变化；完全浸入水之后，水深才保持不变。由式{1}可知漂浮时潜水器的下半部分恰好浸在水中。设匀速下沉阶段潜水器浸水深度为x，如图2所示，排开的水使得水面上升，则

H'=H0+S1（x-x0）/S2⑦

图 2  潜水器下沉过程水面变化示意图

由匀速下沉过程分析得到的式{4}改写为

F=ρ水gS1（H'-l）-G潜⑧

当潜水器完全浸入水中时，x=2x0，代入式{7}可知，潛水器下沉后水深共变化了

则水的实际深度为

H'=H0+ΔH=25.5 cm⑩

将其代入式{8}，并令l=0，可求得潜水器沉底静止后的吸力为

F'0=ρ水gS1H'-G潜=20.5 N{11}

结合已计及水深变化得到的式{3}，这种情况下，铁板上的压强为

1.3.2 忽略水深变化的简化模型

式{3}所得的潜水器沉底时水和潜水器的总重力等于初始状态下的重力，即水的重力保持不变，说明此处已经是考虑水深变化的。如果忽略水深变化，即水深保持为常量H0=25 cm，那么潜水器下沉全过程中，容器内水的体积均为

V0=S2H0-S1d0=2.4×104 cm3{13}

其中d0为潜水器边长，即d0=10 cm。因此，水的重力为

G'水=ρ水V0g=240 N{14}

那么，第（3）问所求的压强应为

1.3.3 模型简化的科学性分析

由以上分析可见，如果考虑水深变化，吸力的分析和计算比较困难。真题中指出“水深变化的影响忽略不计”，将水深视为常量，简化了模型，一定程度上降低了科学推理的难度，符合“双减”背景下的中考命题要求。但这简化了的模型是否合理呢？从真实情境问题构建简化的物理模型时，需要兼顾模型的科学性、严谨性。某个微小量忽略不计，不代表与该物理量相关的其他物理量也一定能够忽略不计，因为当微小量A乘以一个较大的值，或除以较小的值后所得到的新物理量B，在所研究的问题中可能已不可视为微小量。

对于建模过程中，某物理量是否可以作为微小量的判定，可以借鉴于中学物理实验中对于实验误差允许范围的界定。一般情况下，当测量值相较于真实值的变化在5%的范围内，则认定该测量值是较为准确[ 3 ]。由此可知，在研究的问题中，若某物理量相对于真值的偏差小于5%，则认定该物理量对问题的影响足够小，可视其为微小量，其影响作为次要因素忽略不计，进而简化模型。

下面研究真题中几个与水深变化相关的物理量，即潜水器完全浸入后的水深H、容器内水的总重力G、潜水器沉底后的吸力F以及潜水器沉底后铁板上的压强p，通过对比它们在水深变化忽略前后的值来讨论模型简化是否合理。

由式{9}和式{10}可知，潜水器完全入水后导致的水深变化量？驻H远小于实际水深，因此真题将？驻H视为微小量，忽略不计。以计及水深变化的实际模型中的值为标准值，简化模型的水深的误差仅为1.96%，如表1所示。由表1第4列可以发现，忽略与计及水深变化的两种情况下，重力、吸力和压强的差值均正比于水深变化？驻H，相较于各自的标准值，简化值对应的百分误差分别为2.04%、2.44%、2.03%，均小于5%，说明？驻G、？驻F和？驻p也都可以视为微小量。由此可知，在研究第（3）问所提及的问题中，水深变化的影响确实可以忽略不计。另外，题干还指出容器是“薄壁”的，即壁厚度d→0，则与其成正比的容器质量也可以是微小量，“不计容器的质量”也是成立的。因此，本试题简化了的物理模型是科学的，命题是严谨的。

官方宣布的参考答案中，第（3）问所求的压强等于式{4}所示的2700 Pa，那么，相应的百分误差仅0.18%，更接近于真实问题情境。但“水深变化的影响忽略不计”这一条件，是仅适用于吸力F的计算？还是也适用其他物理量的计算？题干中的表述，可能让审题人产生误会，命制题目时应严谨，以防出现理解上的分歧，比如可以直接指明“计算吸力时不计水深变化的影响”。

2 引发类似问题的思考

中考试题对初中教学具有较强的导向作用。以上关于真题的讨论与分析引发了教学中物理模型的建构及简化处理的思考，比如初中物理中重力与质量的比值g。

初中物理教学中，一般习以为常地将g认定为恒定值9.8 m/s2，更多时候粗略取值为10 m/s2。实际上，g认定为常数的过程包含模型简化的思路，教师可以适当地拓展，将万有引力定律超前给出，然后取一些特殊位置上的g值加以对比，突出微小量的判断依据，初步培养学生建构物理模型的意识和能力，同时认识到“适用条件或范围”的重要性。

若在地球之外，比如中国空间站，相对于地球海平面处的？驻g还是可忽略的微小量吗？有关研究表明空间站是一个微重力环境[ 4 ]，空间站内的重力加速度g3=9.8×10-10 m/s2，约为g1的百亿分之一，趋近于零，相对于海平面重力加速度的变化？驻g≈g1，变化非常显著，相对误差远远大于5%，说明？驻g不再是微小量。课堂上，以天宫课堂第一课中分别出现在北京和空间站的乒乓球的重力差值为例（如图3所示），让学生认识到同一个物理量在不同问题中的影响程度的变化，深刻理解微小量的意义。

3 总结

本文以2022年福建中考物理的压轴计算题为研究对象，定量分析水深变化及相关物理量对所研究问题的影响。因简化值相对于真值的偏差均小于5%，认定水深变化对所研究问题的影响足够小，可视为微小量，在从真实情境构建物理模型的过程中，属于次要因素，可忽略不计，从而肯定了该模型简化的科学性和命题的严谨性。在此基础上，探讨了如何通过重力与质量的比值的教学过程，引导学生深刻认识“适用条件或范围”，学会具体问题具体分析，训练学生的模型建构和科学推理等科学思维能力。同时，试题模型的科学简化研究，有利于提高课后作业设计的质量，有效避免题海战术，符合“双减”背景下“减负提效”的要求。

参考文献：

［1］ 中华人民共和国教育部. 义务教育物理课程标准（2022年版）[S]. 北京： 人民教育出版社， 2022.

［2］ 李忠相.例談日常生活情境类试题的命制要领[J].物理教学，2023，45（2）： 61-63，48.

［3］ 蔡钳. 由“铁球下落”引发的思考[J]. 物理教师， 2022， 43（7）： 61-63.

［4］ 黄玉梅. 谈太空授课中的几个问题[J]. 物理教学， 2019， 41（4）： 78-80.