连续刚构桥合龙顶推力计算方法研究
2023-09-27余钱华唐兵高齐松
余钱华,唐兵,高齐松
(长沙理工大学 土木与建筑学院,湖南 长沙 410004)
近年来,随着交通运输产业的飞速发展,桥梁发挥着越来越重要的作用。预应力连续刚构桥以其伸缩缝少、行车舒适、施工技术成熟、对复杂山区条件适应性良好等优势,得到了快速发展和广泛应用[1]。大跨径连续刚构桥在收缩徐变、温度和荷载的影响下,会在跨中下挠、墩顶处沿纵桥向发生水平位移,导致桥梁结构内部产生较大的次内力,这对桥梁的安全运营是颇为不利的。在施工中,常采用设置预拱度的方式抵消主梁在恒载作用下的挠度,并在中跨合龙口两端施加一对大小适中的顶推力来减少主梁下挠引起的墩顶纵桥向水平位移。许多学者对此进行了大量研究。邹毅松等[2]通过力法方程推导了顶推力与墩顶相对水平位移的关系。仇明等[3]通过力学基本原理,推导了变截面箱梁墩顶相对水平位移的解析式。任翔等[4]以非对称连续刚构桥为依托,分析了非对称顶推力与对称顶推力对主梁挠度及桥墩受力的影响。颜东煌等[5]基于影响矩阵,分析了大跨PC连续刚构桥在合龙段施工的预顶力优化计算方法。宋健[6]计算了多跨连续刚构桥在不同合龙顺序下对应的顶推力,得出合理的顶推力对成桥后期主梁线形平顺及桥墩稳定性有利的结论。吴锋等[7]提出了连续刚构桥基于多目标线性规划方法的合龙顶推力的计算方法。陈金盛[8]以结构受力和变形为基础,计算了桥梁合龙顶推力。本研究拟基于有约束的墩顶水平位移平方和最小化来计算顶推力,以期为类似工程提供参考。
1 优化方法介绍
1.1 约束最优化问题
约束最优化问题[9]是指具有约束条件的非线性规划问题。其最小化问题的一般形式为:
可采用拉格朗日乘子法或罚函数法来求解。
1.2 合龙顶推力优化
在桥梁后期运营阶段,若桥梁墩顶无水平位移,桥墩底部所受弯矩相对较小,不会产生过大的拉应力,则墩底不存在开裂的风险,这种状态被称为理想状态。基于该理想状态,取桥梁双肢薄壁墩每肢墩顶处的主梁截面为控制截面,在中跨合龙前施加一对顶推力,采用在后期运营阶段中控制截面墩顶水平位移平方和最小的方法来求解最优顶推力的大小。控制截面墩顶的水平位移的方程组为:
式中:di是优化目标阶段第i个墩顶控制截面位移;xi是第i个合龙口处顶推力;aim是当在第m个合龙口处施加单位力引起第i个墩顶控制截面位移;dig是无顶推时第i个墩顶控制截面位移。
1) 目标函数。
如果每个控制截面的水平位移的平方能同时达到最小,这将是最理想的状态,但在实际中这很难做到。因此,将每个控制截面水平位移的平方和作为最小化的目标函数,其表达式为:
2) 约束方程。
在确定最优顶推力时,需要确保桥墩底部不开裂,即墩底截面拉应力、压应力均满足《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)的要求。因此,将墩底应力作为约束条件,则该优化问题就变成了有约束优化问题。墩底应力约束方程为:
式中:xi是第i个合龙口处顶推力;bim是当在第m个合龙口处施加单位力引起第i个墩底控制截面应力;σig是无顶推时第i个墩底控制截面应力;σt、σc分别是施工阶段允许拉应力和允许压应力。
2 实例分析
2.1 工程概况
列夕特大桥是湖南省湘西州一座大跨径连续刚构桥,其孔跨布置为110+235+110 m。其连续箱梁预应力采用纵向和竖向双向预应力体系,高度按1.8次抛物线变化,0号梁段高为14.59 m,中跨合龙梁段高为5.59 m。桥墩为双肢空心矩形墩,1#墩高为53.00 m,2#墩高为64.00 m。桥梁立面和主梁横断面分别如图1~2所示。主梁单个T构共28个节段,箱梁0#、1#块各有长为0.50 m的部分在托架上进行施工,其总长为16.00 m,其余梁段采用挂篮悬臂进行浇筑。边跨长为3.50 m的现浇段采用搭设支架进行浇筑。全桥按先边跨,再中跨的顺序合龙。
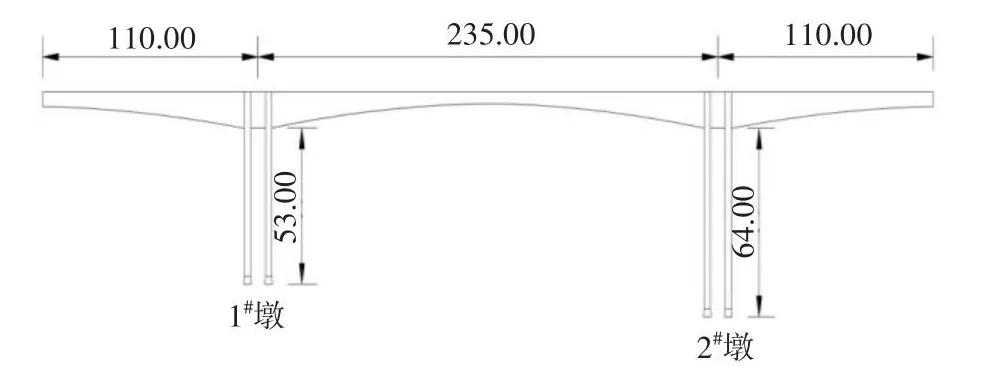
图1 列夕特大桥立面布置图(单位:m)Fig.1 Elevation layout of Lixi Bridge (unit: m)
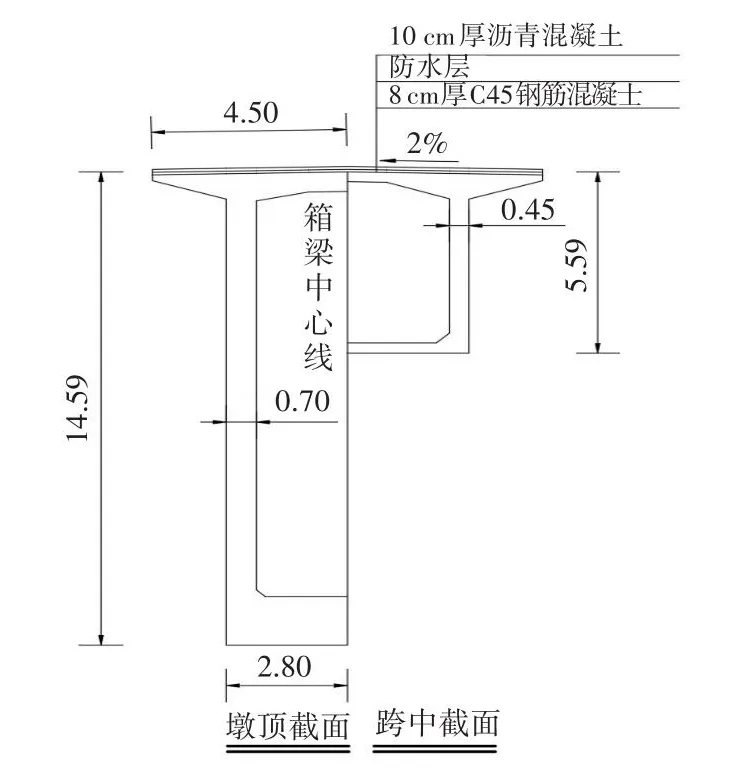
图2 列夕特大桥主梁横断面图(单位:m)Fig.2 Cross section of main girder of Liexi Bridge (unit: m)
2.2 有限元模型建立
采用Midas Civil有限元软件模拟列夕特大桥在施工阶段及成桥10 a后的应力与位移情况,桥梁结构有限元模型如图3所示。主梁和桥墩均采用梁单元模拟,主梁单元的划分以该桥结构施工工序为依据,在桥墩过人孔处进行单元细化。墩底采用固定约束,墩与梁连接采用弹性连接中的刚性连接。在搭设满堂支架施工边跨现浇段,选择其中1个节点约束其竖向与纵向位移,其余节点仅约束其竖向位移,体系转换后在边跨支座处仅约束其竖向位移。

图3 桥梁结构有限元Midas Civil计算模型Fig.3 Finite element Midas Civil calculation model of bridge structure
2.3 合龙顶推力优化计算
为分析单位顶推力对该桥成桥10 a后的墩顶水平位移和墩底应力的影响,采用Midas Civil有限元软件模拟整个桥梁的施工过程,计算和分析在跨中顶推阶段分别施加1 000、2 000、3 000、4 000 kN的顶推力对成桥10 a后墩顶水平位移和墩底左、右缘应力的影响,计算结果分别如图4~6所示。在图4~6中,规定位移右向为正方向,左向为负方向;规定应力受拉为正,受压为负。
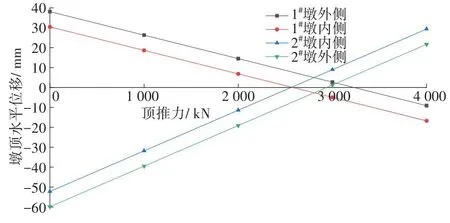
图4 成桥10 a后顶推力与墩顶水平位移关系Fig.4 Relationship between jacking thrust and horizontal displacement of pier top 10 years after completion of bridge
从图4可以看出,当只考虑顶推力变化,且桥梁整体结构处于线弹性时,在一定范围内,墩顶水平位移与顶推力之间呈线性关系,即每增加1 000 kN的顶推力,在各侧墩顶产生的水平位移增量的绝对值大致相同。这表明主梁的收缩徐变基本不受顶推力影响。1#墩每增加1 000 kN的顶推力,其墩顶水平位移减小11.8 mm;2#墩每增加1 000 kN的顶推力,其墩顶水平位移增加20.4 mm。
从图5~6可以看出,当只考虑顶推力变化,且桥梁整体结构处于线弹性时,在一定范围内,墩底应力与顶推力之间呈线性关系,即每施加1 000 kN顶推力,在1#、2#墩底左、右缘产生的应力增量的绝对值基本不变。其中,1#墩外侧左、右缘应力增量的绝对值分别0.5、0.7 MPa;1#墩内侧左、右缘应力增量的绝对值分别为0.7、0.5 MPa;2#墩内侧左、右缘应力增量的绝对值分别为0.6、0.8 MPa;2#墩外侧左、右缘应力增量的绝对值分别为0.8、0.6 MPa。
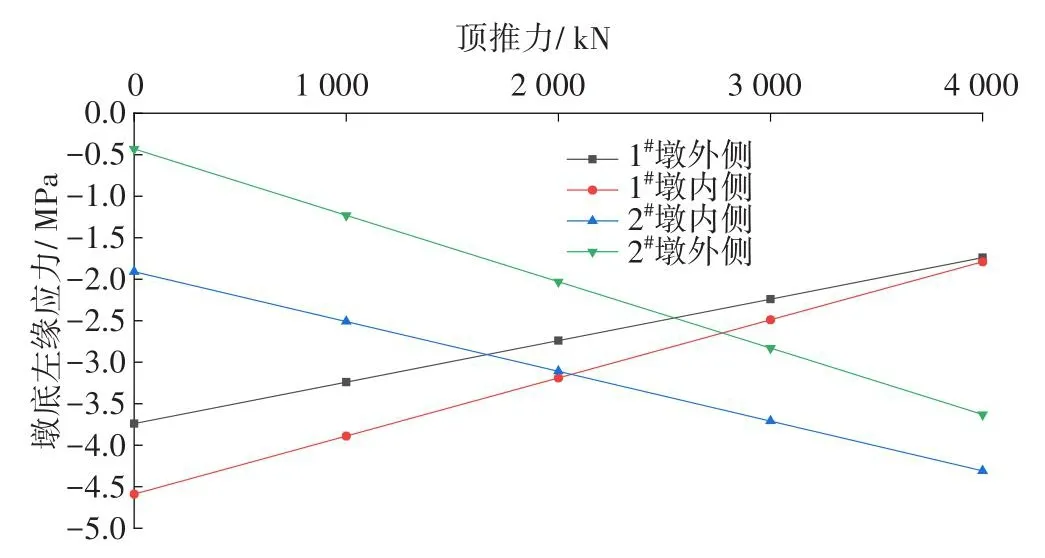
图5 成桥10 a后顶推力与墩底左缘应力关系Fig.5 Relationship between thrust force and stress at left edge of pier bottom 10 years after completion of bridge
由于列夕特大桥只有一个中跨顶推合龙口,所以可将式(2)的墩顶截面位移表达式改写为:
式中:d4×1是墩顶水平位移矩阵;A4×1是合龙顶推力位移影响系数矩阵;dg,4×1是无顶推初始位移矩阵。
d4×1与dg,4×1中每个元素的单位为mm,位移影响系数矩阵中每个元素的单位为mm/kN,合龙顶推力的单位为kN,其大小为合龙顶推力系数x的值乘1 000。同理,墩底应力也可改写为:
式中:σ4×1是墩底应力矩阵;B4×1是合龙顶推力应力影响系数矩阵;σg,4×1是无顶推初始应力矩阵。
分析图4,可得到墩顶水平位移矩阵:
分析图5,可得墩底左缘应力矩:
分析图6,可得墩底右缘应力矩阵:
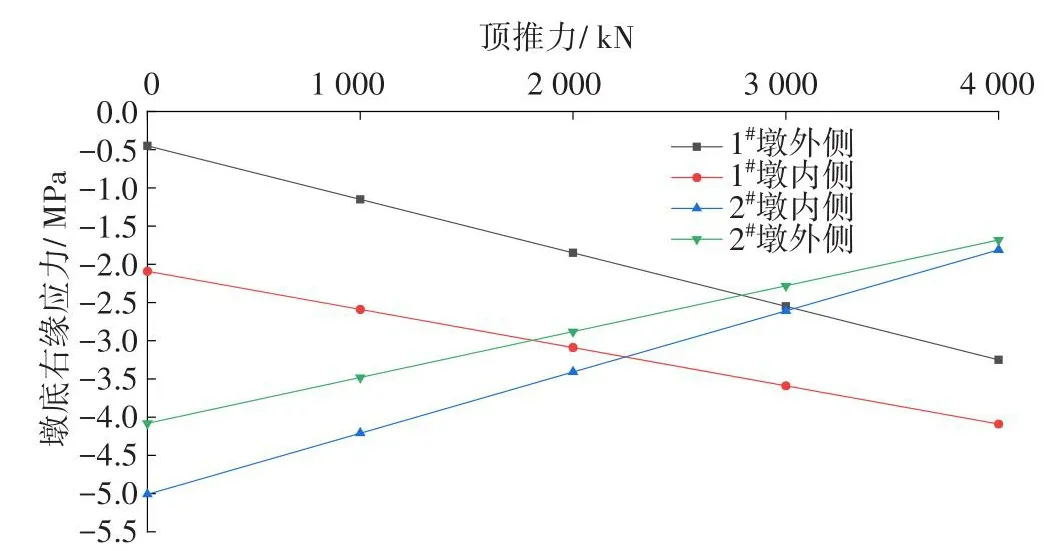
图6 成桥10 a后顶推力与墩底右缘应力关系Fig.6 Relationship between thrust force and stress at the right edge of pier bottom 10 years after completion of bridge
取成桥10 a后为优化目标阶段,则有:
其中,
墩底左缘应力约束条件为:
墩底右缘应力约束条件为:
利用MATLAB数值计算软件,对式(7)~(10)的约束规划问题进行求解,得到顶推力系数x为2.788,由于这些位移影响系数矩阵、应力影响系数矩阵是按合龙顶推力每增加1 000 kN计算得到的,考虑该桥具体情况,其顶推力应为2 788 kN,再考虑施工中千斤顶施加力的方便性,最终,将施工顶推力取整为2 800 kN。
2.4 顶推合龙阶段桥墩应力验算
在按顶推合龙方案的施工阶段,分别计算墩顶、墩底截面的应力,结果见表1。
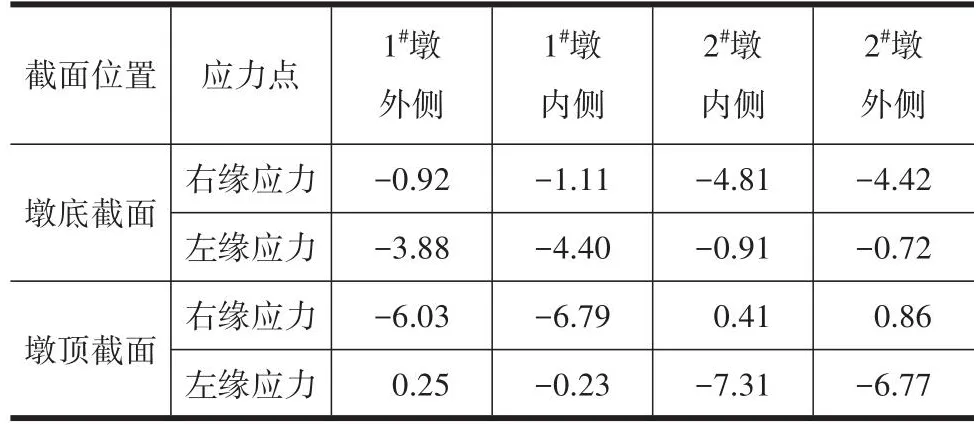
表1 顶推阶段桥墩截面应力Table 1 Pier section stress in the pushing stage MPa
由表1可知,在施加2 800 kN顶推力的合龙阶段,在1#墩墩顶外侧左缘、2#墩墩顶右缘位置均出现了拉应力,其中,最大拉应力为0.86 MPa,出现在2#墩外侧右缘,最大压应力为7.31 MPa,出现在2#墩内侧左缘。在该合龙过程中出现的最大拉应力与最大压应力均符合《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)中的要求。据此可判断:在顶推过程中,桥墩强度满足规范要求,可确保顶推过程中的桥梁安全。
3 顶推合龙对桥梁应力及变形分析
文献[10]~[12]分析了按顶推合龙方案施工对桥梁线形及应力等方面的影响。本文以成桥10 a后为分析阶段,分别比较了在恒载作用下,无顶推合龙与顶推合龙两种方案对主梁应力、主梁竖向位移、墩顶水平位移、墩底应力的影响。
3.1 主梁应力对比分析
在对主梁应力进行对比和分析时,考虑在恒载作用下,成桥10 a后,无顶推合龙与顶推合龙两种方案对主梁上缘应力、下缘应力的影响,两种方案的计算结果分别如图7~8所示。
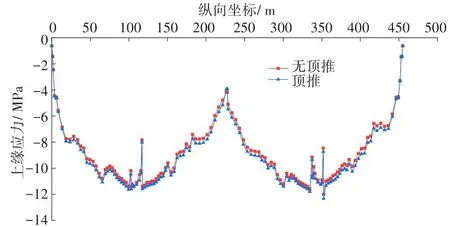
图7 恒载作用下10 a后主梁上缘应力Fig.7 tress on upper edge of main beam after 10 years under dead load
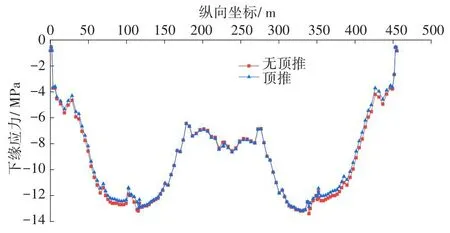
图8 恒载作用下10 a后主梁下缘应力Fig.8 Stress at lower edge of main beam after 10 years under dead load
从图7~8可看出,两种合龙方案对主梁应力变化均不明显。在桥梁跨中区域,顶推合龙与无顶推合龙两种方案的主梁上缘最大压应力分别为12.31和12.00 MPa,两者几乎相等;顶推合龙与无顶推合龙两种方案的主梁下缘最大压应力分别为12.99和13.20 MPa,两者的差值为0.21 MPa。这主要由于顶推反力主要由桥墩变形承担,在桥梁运营10 a后,该变形会被混凝土收缩徐变抵消一部分,其顶推反力也将减少。
3.2 主梁竖向位移对比分析
在对主梁的竖向位移进行对比和分析时,考虑在恒载作用下,成桥10 a后,无顶推合龙与顶推合龙两种方案对主梁竖向位移的影响,两种方案的计算结果如图9所示。
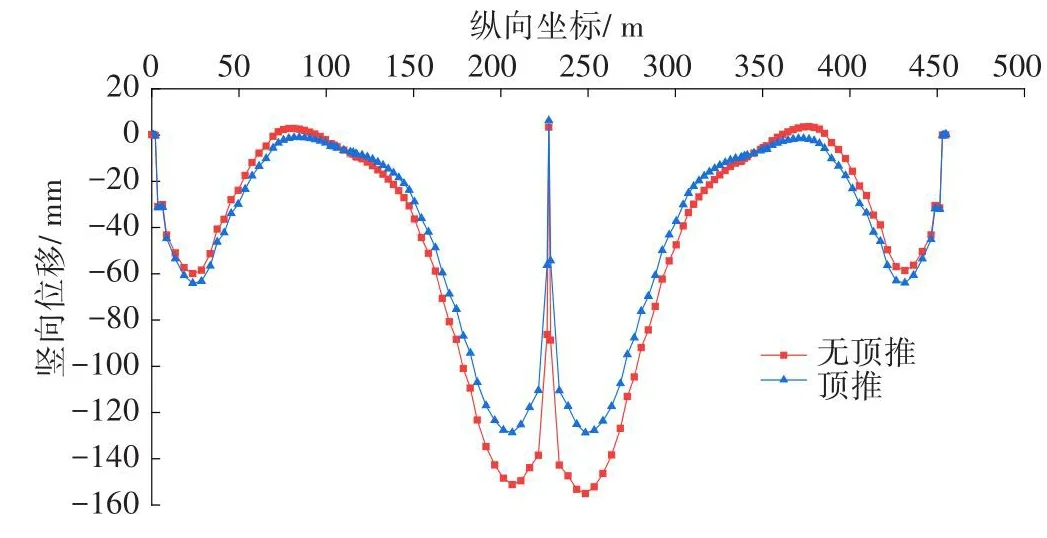
图9 恒载作用下10 a后主梁竖向位移Fig.9 Vertical displacement of main beam under dead load after 10 years
从图9可以看出,顶推合龙方案的边跨竖向位移略大于无顶推合龙方案的。在靠近2#墩边跨跨中截面,两种方案的竖向位移相差最大,顶推合龙的竖向位移为-29.15 mm,而无顶推合龙的竖向位移为-22.07 mm,其差值为7.08 mm。无顶推合龙引起的中跨竖向位移明显大于顶推合龙的,在靠近跨中截面,两种方案的竖向位移相差最大,无顶推合龙的竖向位移为-88.74 mm,而顶推合龙的竖向位移为-56.72 mm,其差值为32.02 mm。在顶推作用下,桥墩会往各自边跨支座方向发生变形,根据墩顶处的变形协调条件,主梁跨中会产生向上的位移,边跨会产生向下的位移,这对改善桥梁由于收缩徐变引起跨中下挠问题是有利的。但仅依靠顶推作用,并不能完全解决主梁下挠问题,因此,必须在施工过程中,给桥梁施加合理的预拱度。
3.3 桥墩墩顶水平位移对比分析
在对墩顶水平位移进行对比和分析时,考虑恒载作用下,成桥10 a后,无顶推合龙与顶推合龙两种方案对墩顶水平位移的影响,两种方案的计算结果见表2。
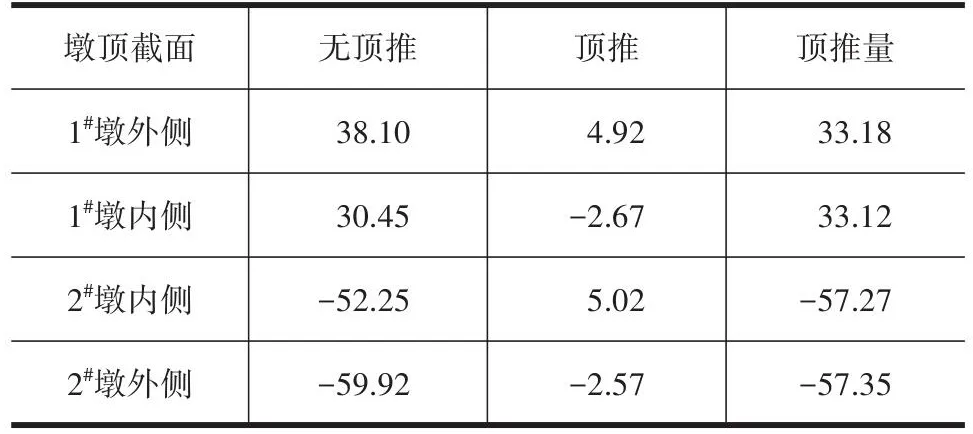
表2 成桥10 a后墩顶水平位移Table 2 Horizontal displacement of pier top 10 years after completion of bridge mm
由表2可知,1#墩内、外侧的顶推量分别为33.18、33.12 mm,分别占其无顶推总水平位移的87%、109%;2#墩内、外侧的顶推量分别为57.27、57.35 mm,分别占无顶推水平位移的110%、96%。2#墩相应位置的顶推量均大于1#墩的,这主要由于2#墩位置较高,其抗推刚度较小。通过对成桥10 a后墩顶水平位移的分析与比较,顶推合龙的墩顶的最大水平位移为5.02 mm。顶推合龙方案能较好地确保桥墩处于垂直状态。
3.4 桥墩墩底应力对比分析
在对墩底应力进行对比和分析时,考虑在恒载作用下,成桥10 a后,无顶推合龙与顶推合龙两种方案对墩底应力的影响,两种方案的计算结果见表3。
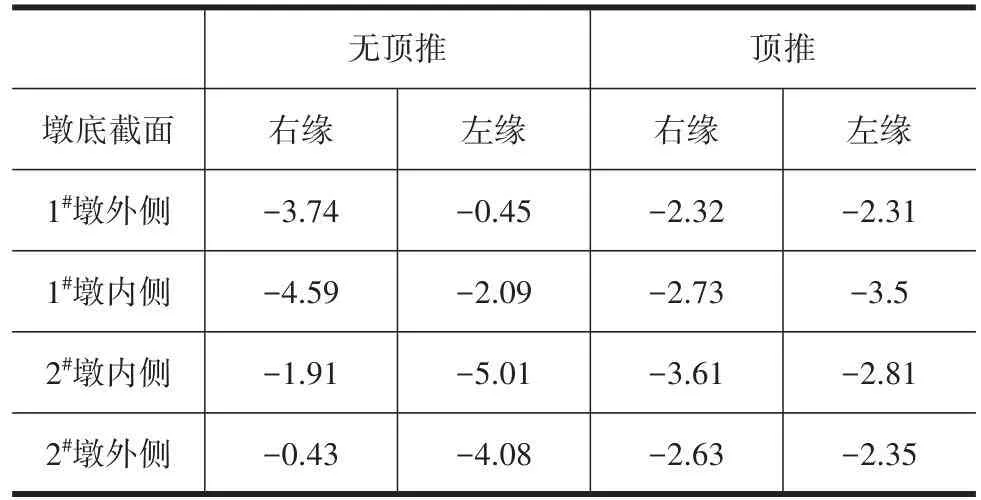
表3 恒载作用下10 a后墩底应力Table 3 Pier bottom stress after 10 years under dead load MPa
由表3可知,顶推合龙墩底压应力分布较均匀,其最小压应力为2.32 MPa,各墩内外侧都有一定的压应力储备。在无顶推合龙方案中,2#墩外侧右缘压应力仅为0.43 MPa。因此,在之后的桥梁运营过程中,荷载及温度变化可能使桥梁产生较大的拉应力,导致混凝土开裂。
4 合龙温差对顶推力的影响
对于连续刚构桥这种超静定结构,温度变化会使结构产生温度次应力。在实际施工过程中,令实际合龙温度与设计合龙温度之间的差为△t,即△t=t1-t0(t1为实际合龙温度,t0为设计合龙温度),则由其导致的主梁伸长或缩短的水平位移必须依靠附加顶推力来补偿。如果t1较高,则应增加顶推力,使顶推的水平位移加大。严宗雪等[13]在研究斜拉桥合龙顶推力时,发现合龙温差对顶推力的影响不可忽略。刘文强等[14]对刚构-连续组合体系梁桥合龙温度进行了分析,得出合龙温度在允许范围内越低越好的结论。徐鹏等[15]研究了温度对墩顶水平位移的影响,提出附加顶推力为主墩水平刚度与主梁墩顶水平位移的乘积的结论。当t1>t0,该合龙方案为高温合龙,结构表现为降温效应,墩顶会向中跨方向产生水平位移,合龙时需要增大顶推力来抵消此位移;当t1 表4 温差荷载作用下各墩顶中心水平位移Table 4 Horizontal displacement of pier tops under temperature difference load mm 由表4可知,在一定范围内,1#、2#墩顶中心水平位移与温差呈线性变化,△t每增加5 ℃,1#墩的墩顶水平位移向右增加4.44 mm,2#墩的墩顶中心水平位移向左增加7.32 mm。即单位温差作用下,1#墩的墩顶中心水平位移会向右增加约0.89 mm, 2#墩的墩顶中心水平位移会向左增加约1.46 mm。 从图4可以看出,在此种位移情况下,换算得到所需顶推力的温差系数分别为75.41、71.57,取两者平均值73.49作为顶推力温差系数。因此,考虑合龙温差的顶推力优化计算公式为: 1) 当只考虑顶推力变化,且桥梁整体结构处于线弹性时,在一定范围内,顶推力与墩顶水平位移、墩底应力之间基本均呈线性关系。 2) 通过对顶推施工阶段的墩底应力进行分析发现,在合龙过程中出现的最大拉应力与最大压应力均符合《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362—2018)中的要求。因此,在桥梁顶推过程中,桥墩强度可满足规范要求,桥梁结构处于安全状态。 3) 无顶推合龙方案和顶推合龙方案的主梁应力变化均不明显,特别在跨中区域,两种施工方案的主梁应力几乎相等,两种方案在边跨处的应力稍有区别,其应力最大差值为0.31 MPa,该应力差值出现在靠近2#墩顶的边跨处。 4) 按顶推合龙方案进行施工,可有效地改善桥梁因混凝土收缩徐变引起的跨中下挠问题,与按无顶推合龙方案进行施工相比,其跨中竖向位移最多减少了32.01 mm,改善效果显著。 5) 无顶推合龙方案与顶推合龙两种方案的桥墩最大水平位移分别为59.92、5.02 mm。这表明顶推合龙方案能更有效地减小墩顶的水平偏位,能更好地确保桥墩处于垂直状态,提高桥梁结构的稳定性和安全性,这对桥墩受力是非常有利的。 6) 若按无顶推合龙方案施工,桥梁最小压应力为0.43 MPa;若按顶推合龙方案进行施工,桥梁最小压应力为2.32 MPa,表明顶推方案合理、可行。 7) 在顶推合龙的过程中,要考虑合龙温度对顶推的影响。墩顶中心水平位移与温差之间呈线性关系,实际合龙温度比设计合龙温度每升高1 ℃,须额外施加73.49 kN的顶推力。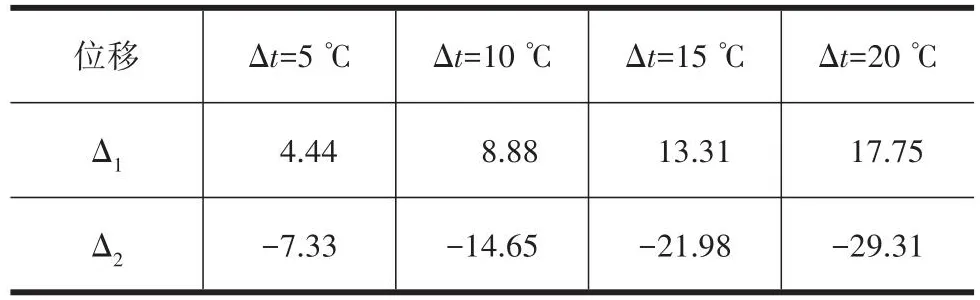
5 结论
