栓钉及荷载对简支组合梁滑移和挠度的影响分析

雷启南，王鹏，南洪良，周东华，高永林

（1.昆明理工大学 建筑工程学院，云南 昆明650500；2.昆明理工大学 建筑与城市规划学院，云南 昆明 650500）

目前，有关组合梁界面滑移的研究有很多［1-8］，组合梁通常为使用栓钉进行连接的梁，其界面在不同荷载作用下属于弹性剪切连接（存在滑移），而无剪切连接（自由滑移）与刚性剪切连接（滑移为0）的桥梁状态属于理想状态，其在实际工程中是不存在的。组合梁产生的界面滑移会影响组合梁的刚度，还会对混凝土及钢梁中的内力产生影响，对挠度产生不可忽视的影响。为了准确、快速地计算出组合梁的滑移和变形，周东华等［9］建立了考虑组合梁滑移的挠度计算方法，该方法简化了计算过程，补充了《钢结构规范》（GB 50017—2003）［10］在无剪切连接至完全剪切连接的计算空白，且各参数物理意义更加明晰。曾兴贵等［11］推导出了单元刚度矩阵并采用自编的小型有限元软件进行编程，将该软件的计算结果与解析解结果进行对比，验证了该方法精度更高。这些研究仅考虑了栓钉均匀布置在组合梁中的情况，对于不同布置形式的栓钉组合梁的研究鲜见。解析解的公式冗长，且在不同荷载形式和不同栓钉布置时，不一样的边界条件得到的解析公式也不相同，使用很不方便。因此，本研究采用ANSYS软件建立组合梁的有限元模型，分析在不同栓钉布置和不同荷载作用下，这两种参数对组合梁的界面滑移和挠度的影响，验证本模型的正确性，并研究不同栓钉布置导致组合梁截面内力的影响，分析栓钉间距影响界面内力与变形的原因，并对栓钉布置进行优化，减小组合梁的滑移和挠度，以期为类似工程设计和计算提供借鉴。

1 组合梁变形计算

1.1 组合梁变形计算解析解

在解析解中，对于不同荷载作用时组合梁的界面滑移均采用式（1）进行计算［11］。

式中：S为组合梁界面滑移；T为剪力流，为均匀分布在梁中的单个剪切连接件的刚度，e为梁单元中均匀分布的剪切连接件间距。

荷载分别为均布荷载和集中荷载时，轴力N及挠度f的计算式分别为：

1） 均布荷载。

式中：N为组合梁轴力；M为弯矩；ω为特征系数；l为梁长；q为均布荷载；SEI为组合梁抗弯强度；γ、β分别为系数和组合系数；d为混凝土板中性轴到钢梁中性轴距离。

2） 集中荷载。

式中：N1为组合梁轴力；M1为弯矩；ω为特征系数；l为梁长；P为集中荷载。

由式（2）～（5）可知，在不同荷载工况下，N取值的不同会导致滑移计算式与挠度计算式的不同，并导致解析解计算式复杂化，不便于实际工程计算。

在式（2）～（5）中，ω为特征系数。

式中：SEI，c为混凝土抗弯强度；SEI，s为钢梁抗弯强度；SEA，c为混凝土抗压强度；SEA，s为钢梁抗压强度。

此解析解仅适用于剪切连接件均匀分布在组合梁中的情况。对于非均匀的剪切连接件布置，其解则更为复杂，因此，本研究采用ANSYS软件建立组合梁的有限元模型，进行计算。

1.2 ANSYS模型的建立与计算

1.2.1 组合梁截面参数

混凝土与钢梁截面尺寸如图1所示。

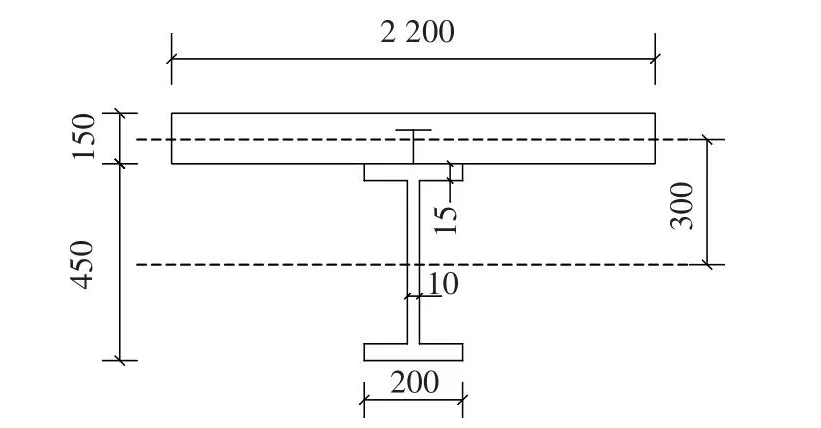
图1 组合梁截面尺寸（单位：mm）Fig.1 Sectional size of composite beam（unit：mm）

假设钢梁与混凝土材料均为线弹性，混凝土的弹性模量Ec为3.0×104MPa，泊松比µc为0.2，钢梁的弹性模量Es为2.10×105MPa，泊松比µs为0.3，单个栓钉连接件刚度k为5.024×104N/mm，均匀分布在组合梁中栓钉的间距e为200 mm；

1.2.2 有限元网格划分

图2为有限元模型网格的划分示意图。

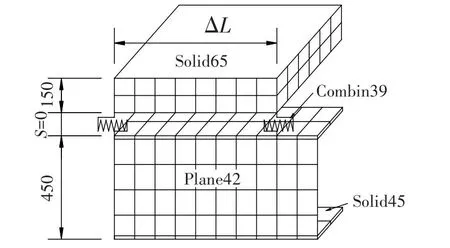
图2 有限元模型网格划分示意Fig.2 Schematic diagram of finite element model

在该有限元模型中，组合梁界面间的栓钉用Combin39弹簧单元模拟，混凝土板及钢梁翼缘分别用实体单元Solid65和Solid45模拟，钢梁腹板则用板单元Plane42模拟。

1.2.3 荷载形式

图3为简支组合梁4种不同荷载形式及其对应的剪力图。

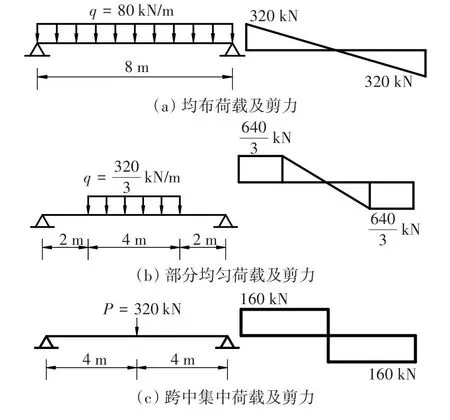
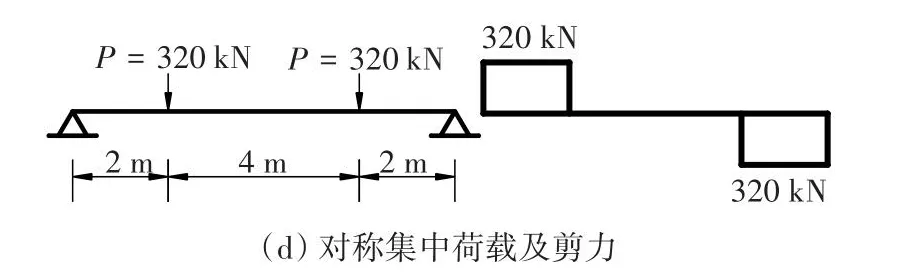
图3 组合梁不同荷载工况和剪力Fig.3 Different load conditions and shear forces of composite beams

荷载大小的选择是由每种荷载形式下组合梁的总剪图面积大小来决定的。

1.3 模型计算结果与分析

荷载均匀布置与部分均匀布时组合梁的滑移的解析解与数值解，见表1，因荷载与支座均对称分布，所以表1仅列出半跨组合梁的滑移值。

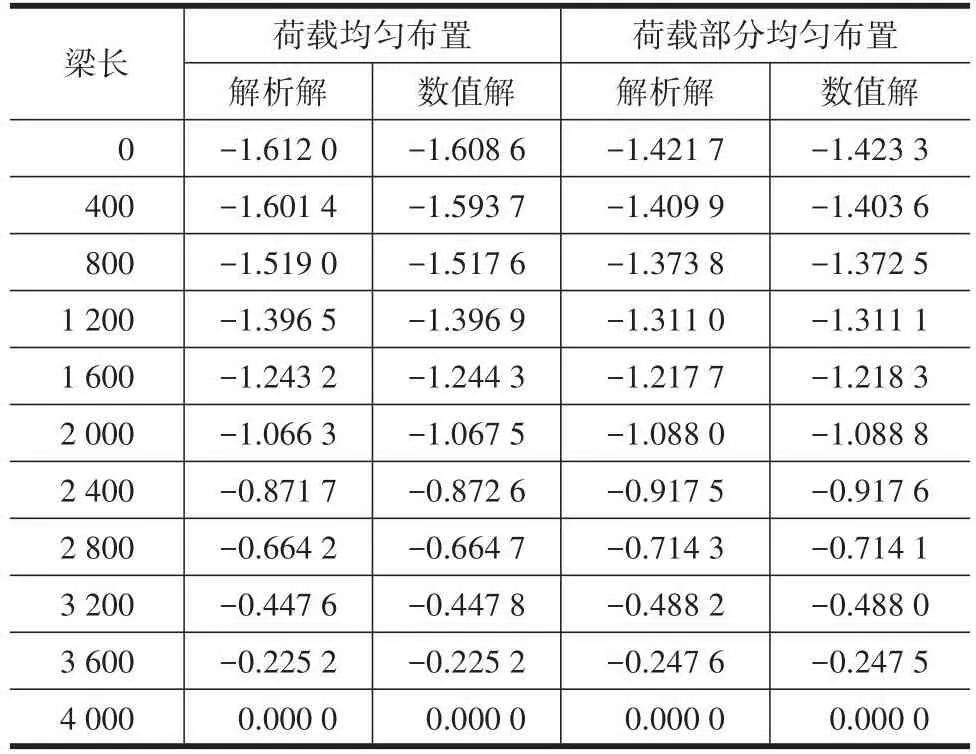
表1 均布与部分均布荷载时的滑移值Table 1 Slide values under uniform and partially uniform loads mm

跨中为集中与对称集中荷载时组合梁的滑移的解析解与数值解，见表2。

猪伪狂犬病毒，除感染猪外，还可以感染多种家畜和野生动物，是一种急性传染性疾病。猪伪狂犬病发病没有季节性限制，春夏秋冬四季均可发生，但以冬春季节气温寒冷、外界应激因素多变造成的发病率和死亡率最高。患病猪和带毒猪可以通过体内分泌物、流产物、尿液、乳汁排毒，健康猪接触这些污染物质后，感染该种病毒的几率极大增加。近年，随着猪养殖产业不断向集约化和规模化方向发展，猪伪狂犬病已经成为严重损害猪养殖产业健康发展的主要病毒性疾病。因此，做好该种疾病的防控，具有重大现实意义。

表2 跨中集中与对称集中荷载时的滑移值Table 2 Slip value of mid-span concentrated and symmetrical concentrated loadmm

由表1～2可知，在4种不同荷载工况下，组合梁滑移的解析解与ANSYS模拟解基本吻合，最大相对误差不超过1%，表明：本研究建立的有限元模型是正确的。

挠度的解析解与数值解不具体展示，经对比两者的挠度计算结果最大相对误差也不超过1%。

2 组合梁的变形分析

2.1 不同荷载形式

图4为4种不同荷载的滑移分布图。从图4可以看出，在4种不同荷载工况下，组合梁的滑移分布呈梁端最大，跨中为0，且随梁长增加呈逐渐减小的趋势。

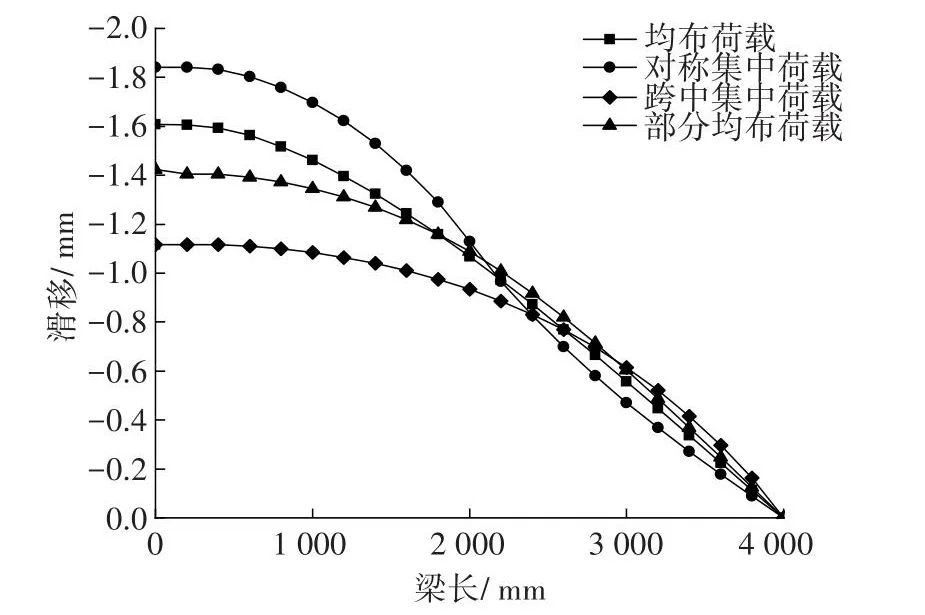
图4 不同荷载工况的滑移（半跨）Fig.4 Slide under different load forms（half span）

在4种不同荷载中，对称集中荷载工况时组合梁梁端滑移最大，在跨中为集中荷载工况下，梁端滑移最小。

图5为4种不同荷载工况的挠度分布图。从图5可以看出，组合梁的挠度分布跨中最大，且抗度在支座端为0，随梁长增加呈逐渐增大的趋势。

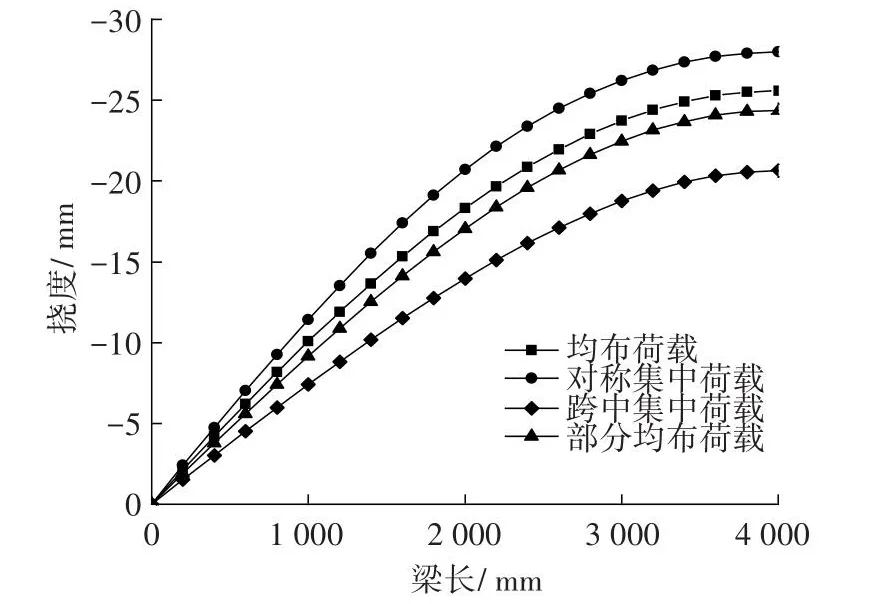
图5 不同荷载工况的挠度（半跨）Fig.5 Deflection distribution under different load forms（half span）

同滑移图类似，对称集中荷载工况的挠度最大，跨中为集中荷载工况的挠度最小。这表明：在剪力图面积大小相同的情况下，对称集中荷载对于简支梁的变形影响最大，而跨中为集中荷载工况的影响最小，其余两种荷载形式的影响介于它们之间。

2.2 栓钉间距不同

图6为对称集中荷载工况时不同栓钉间距挠度分布对比图。

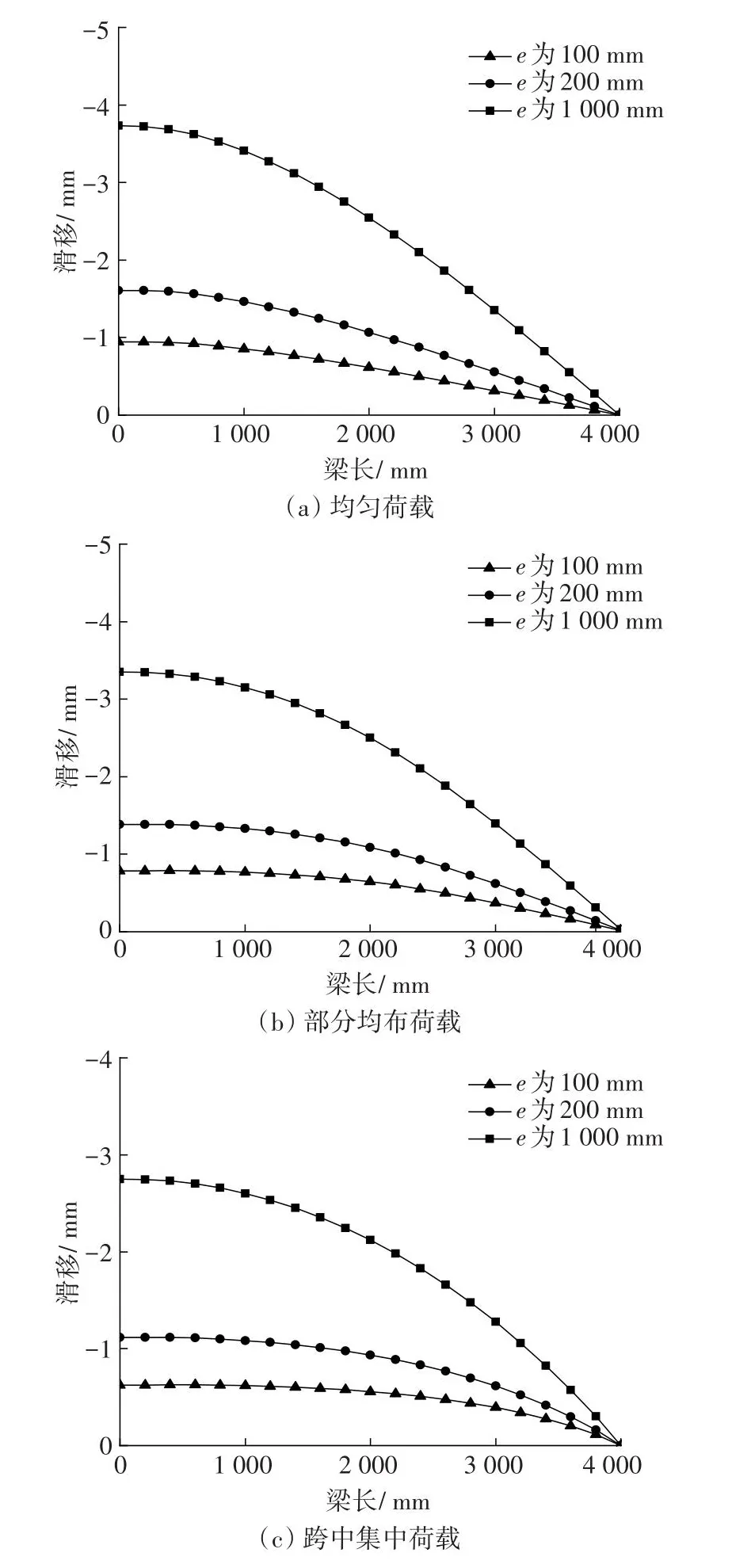
图6 不同栓钉间距时挠度变化对比（半跨）Fig.6 Comparison of deflection distribution at different stud spacing （half-span）

从图6中可以看出，在4种荷载工况下，滑移都随着栓钉间距的增大而增大，并且滑移都是梁端最大，跨中为0，从梁端往跨中逐渐减小。在栓钉间距分别为200、1 000 mm时，滑移增幅明显，表明栓钉间距的不同对简支组合梁滑移的影响很大。

图7为均布荷载的不同栓钉间距挠度变化对比图。

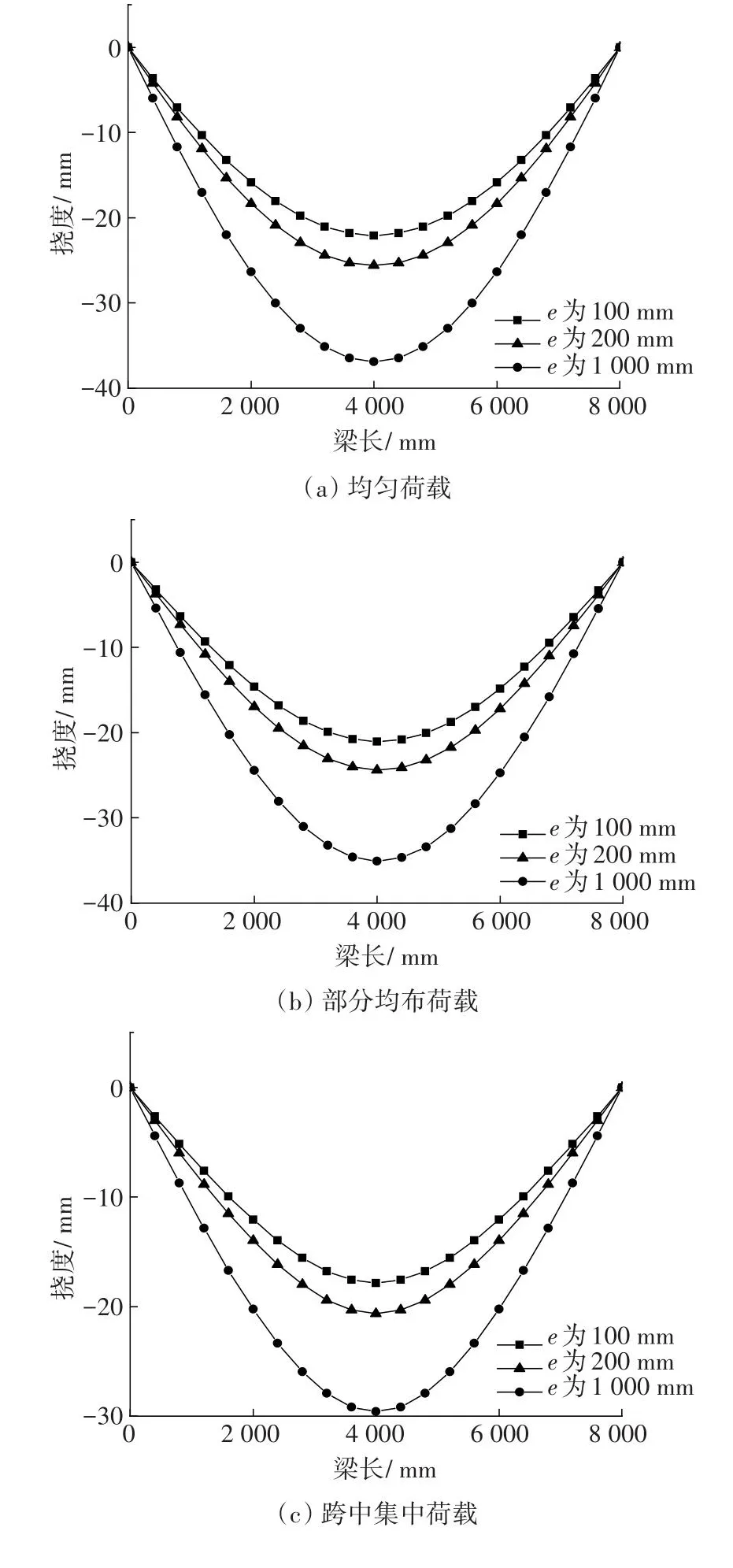
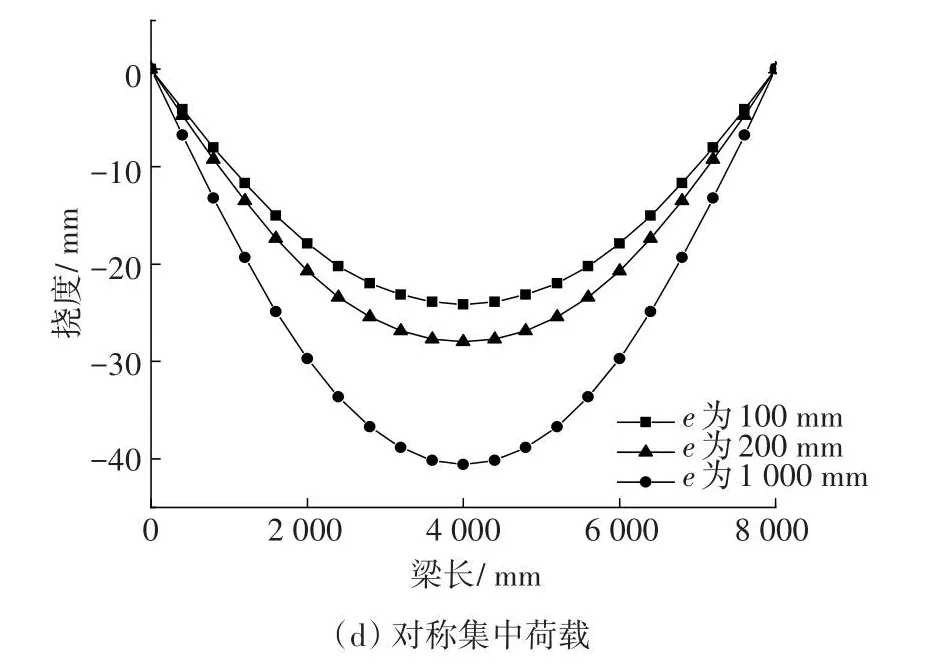
图7 不同栓钉间距的挠度变化对比Fig.7 Comparison of deflection distribution at different stud spacing

从图7可以看出，组合梁的挠度大小也随着栓钉间距的增大而增大，并且挠度分布在跨中最大，梁端为0。这表明栓钉的间距对组合梁的滑移及挠度有不可忽视的影响。

采用ANSYS软件建立的有限元模型，其滑移图与挠度图均符合理论与实际情况，表明：模拟均匀布置栓钉的组合梁变形计算结果是可靠的。

2.3 栓钉分段布置

工程中为方便施工及计算，参考文献［12］，采用如图8所示的均匀布置栓钉方式。但为了降低滑移对组合梁的影响，最为合理的布置栓钉方式显然是图4的布置方式，但在实际工程中，这样的布置方式不便于操作。因此，本研究采用ANSYS有限元软件，模拟栓钉总个数不变，减小梁端处栓钉间距，增大跨中栓钉间距的布置方式。分段均布布置栓钉如图9所示，将栓钉分为两段来布置，分析该工况下组合梁的变形情况。

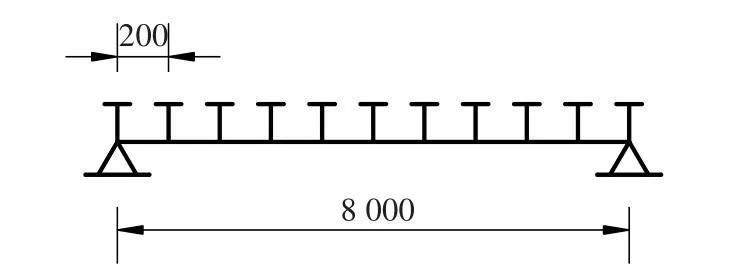
图8 均匀布置栓钉（单位：mm）Fig.8 Evenly spaced studs（unit：mm）

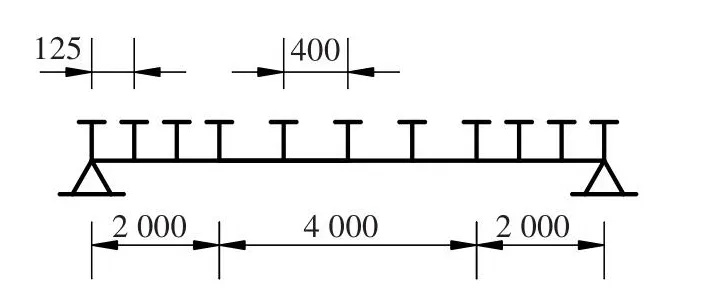
图9 分段均布布置栓钉（单位：mm）Fig.9 Sectional uniform arrangement of studs（unit：mm）

在栓钉刚度k为5.024×104N/mm，均布荷载q为80 N/mm时，若采用图8所示的栓钉布置方式时，梁端的滑移s为1.608 6 mm，跨中挠度w为25.582 3 mm。若采用图9所示的栓钉布置方式时，梁端的滑移s为1.202 4 mm，跨中挠度w为24.089 6 mm。在栓钉刚度k为5.024×104N/mm，跨中集中荷载P为3.2×105N时，若采用图8所示的栓钉布置方式，则梁端的滑移s为1.116 6 mm，跨中挠度w为20.633 2 mm.若采用图9所示的栓钉布置方式，则梁端的滑移s为0.830 5 mm，跨中挠度w为19.705 7 mm。这表明在这两种荷载工况下，均匀布置栓钉分两段组合梁的最大滑移及挠度有明显减小，验证了这样的栓钉布置方式更为合理。

图10为在4种荷载工况下，均匀布置与分段均匀布置栓钉组合梁的滑移大小沿梁长对比。从图10可以看出，采用分段均匀布置栓钉，这4种荷载工况下梁端处的滑移均有显著减少，而跨中的滑移却没有因为跨中栓钉间距的增大而增大，而是基本保持不变。

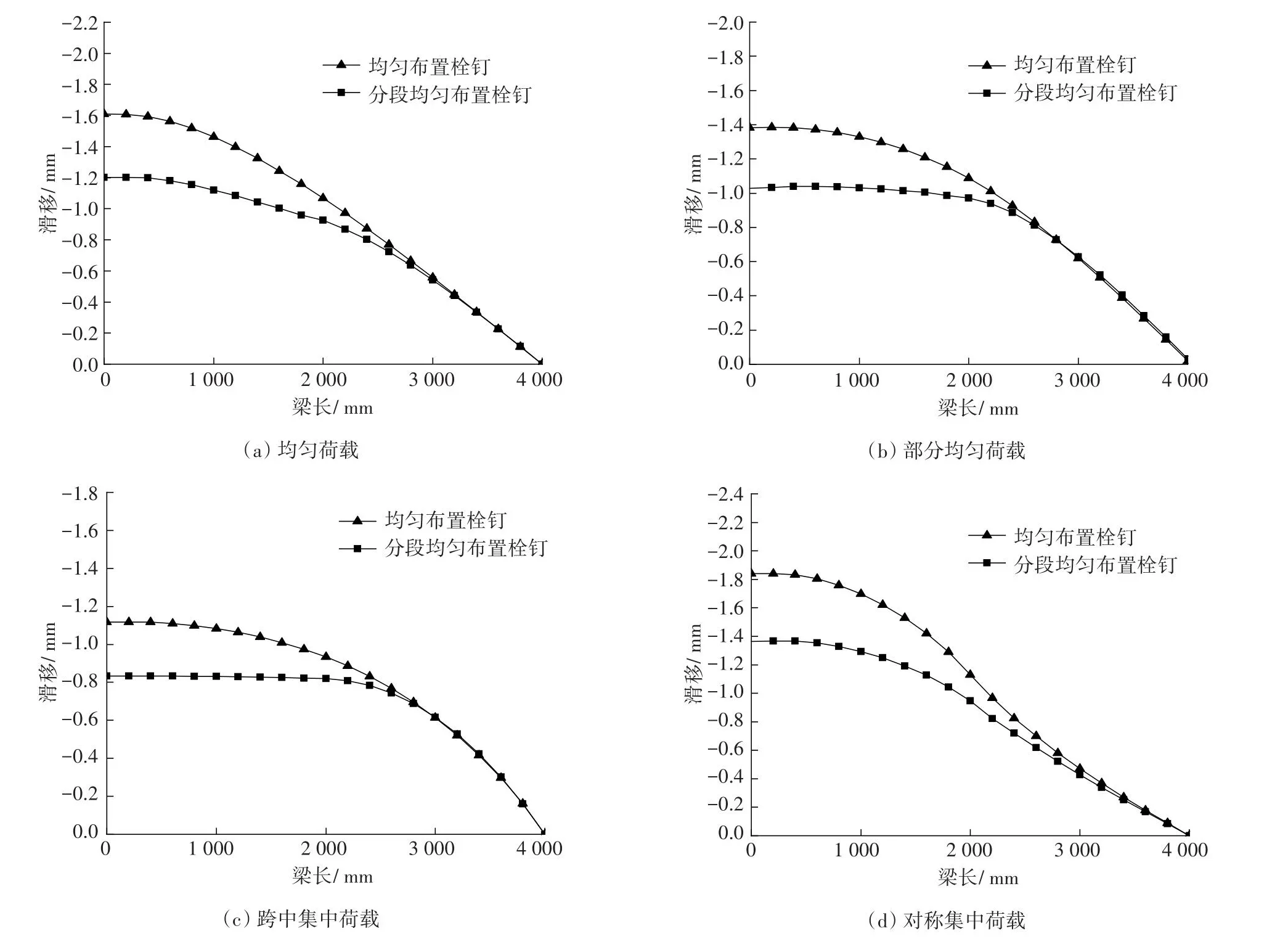
图10 不同荷载、间距时滑移变化对比（半跨）Fig.10 Comparison of slippage distribution at different loads and intervals （half-span）

在4种荷载工况下，均匀布置与分段均匀布置栓钉组合梁的挠度大小沿梁长对比如图11所示。从图11可以看出，在4种荷载下，沿梁长分布的挠度在分两段均匀布置栓钉情况下的长度，全部小于均匀布置栓钉情况下的挠度。

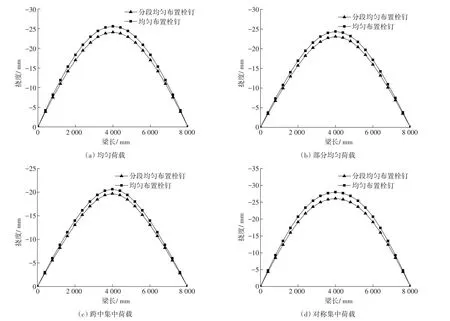
图11 不同荷载、间距时挠度变化对比（半跨）Fig.11 Comparison of deflection changes under different loads and spacing （half-span）

在部分均布荷载工况下，跨中的最大挠度没有因为跨中栓钉间距的增大而增大，其原因是梁端栓钉间距的减小使得最大滑移减小，从而导致跨中的挠度没有因为栓钉间距增大而增大，反而有所减少。

在保持栓钉个数不变的工况中，按本研究的分两段均匀布置栓钉显然更为合理，该布置不仅可以减小梁端最大滑移，也可以相应地减小跨中的最大挠度。工程中如果条件，允许将栓钉按照滑移图的分布来布置是最为合理的。

3 截面内力分析

不同荷载工况时组合梁弯矩的计算式分别为［13］：

式中：M为组合梁承受总弯矩；Mc为混凝土承受弯矩；Ms为钢梁承受弯矩；Ma为组合弯矩；Nc、Ns分别为混凝土及钢梁轴力；d为混凝土板中性轴至钢梁中性轴距离。

3.1 轴力分析

当弹簧刚度k为5.024×104N/mm时，图12为不同荷载工况时组合梁轴力随栓钉间距变化对比。从图12可以看出，栓钉间距e逐渐减小，4种荷载工况下栓钉所承受的轴力N都在增大。

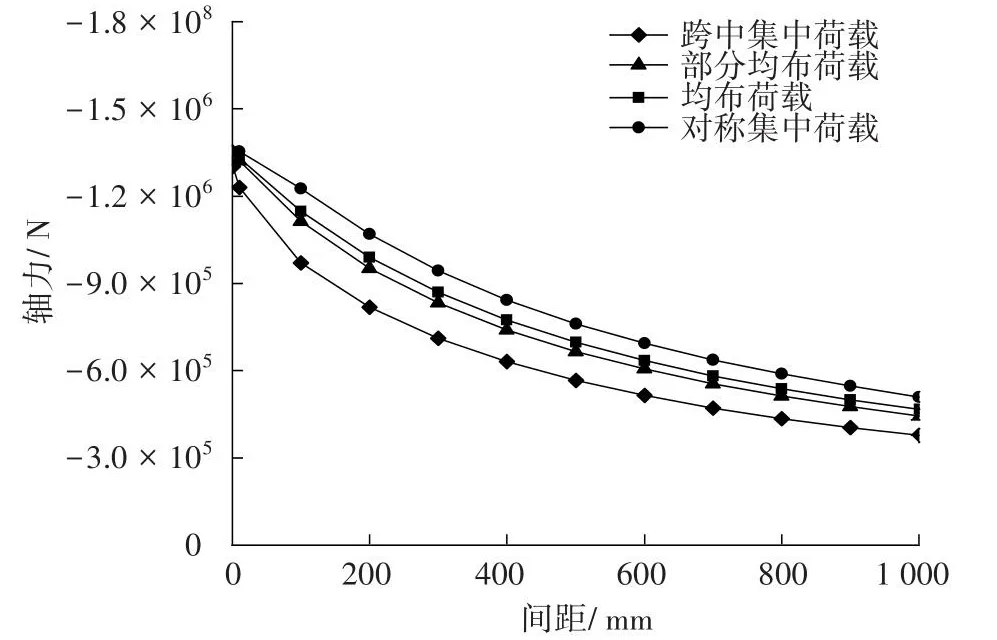
图12 不同荷载、间距时轴力变化对比Fig.12 Comparison of axial force changes under different loads and spacing

从图12还可以看出，当栓钉间距接近0时，其轴力趋近一个固定的数值，意味着随着栓钉间距的减小，栓钉所承担的轴力并不能无限增大。

3.2 弯矩分析

图13为不同荷载工况时组合梁弯矩随栓钉间距的变化规律。从图13可以看出，4种荷载工况下，组合梁弯矩均随着栓钉间距减小。钢梁和混凝土内所承受的弯矩在逐渐减少，而组合弯矩在不断增大，但简支组合梁承受的总弯矩不变，所以由式（7）可知，在组合梁截面参数d不变的情况下，组合弯矩的增大是栓钉数目的增多，导致轴力N增大。栓钉间距的减小，使得组合弯矩增大，而组合梁整体承受的总弯矩大小不变，从而减小了混凝土和钢梁各自承受的弯矩，进而减小了组合梁的滑移及挠度。但栓钉间距的减少对增大组合梁组合弯矩的作用是有限的，当栓钉间距达到一个固定数值后，组合梁组合弯矩便不再增长。所以，另一个增大组合梁组合弯矩的方式就是当N达到最大时，增设托板、增大d来提高组合弯矩，达到减小钢梁及混凝土弯矩的目的。

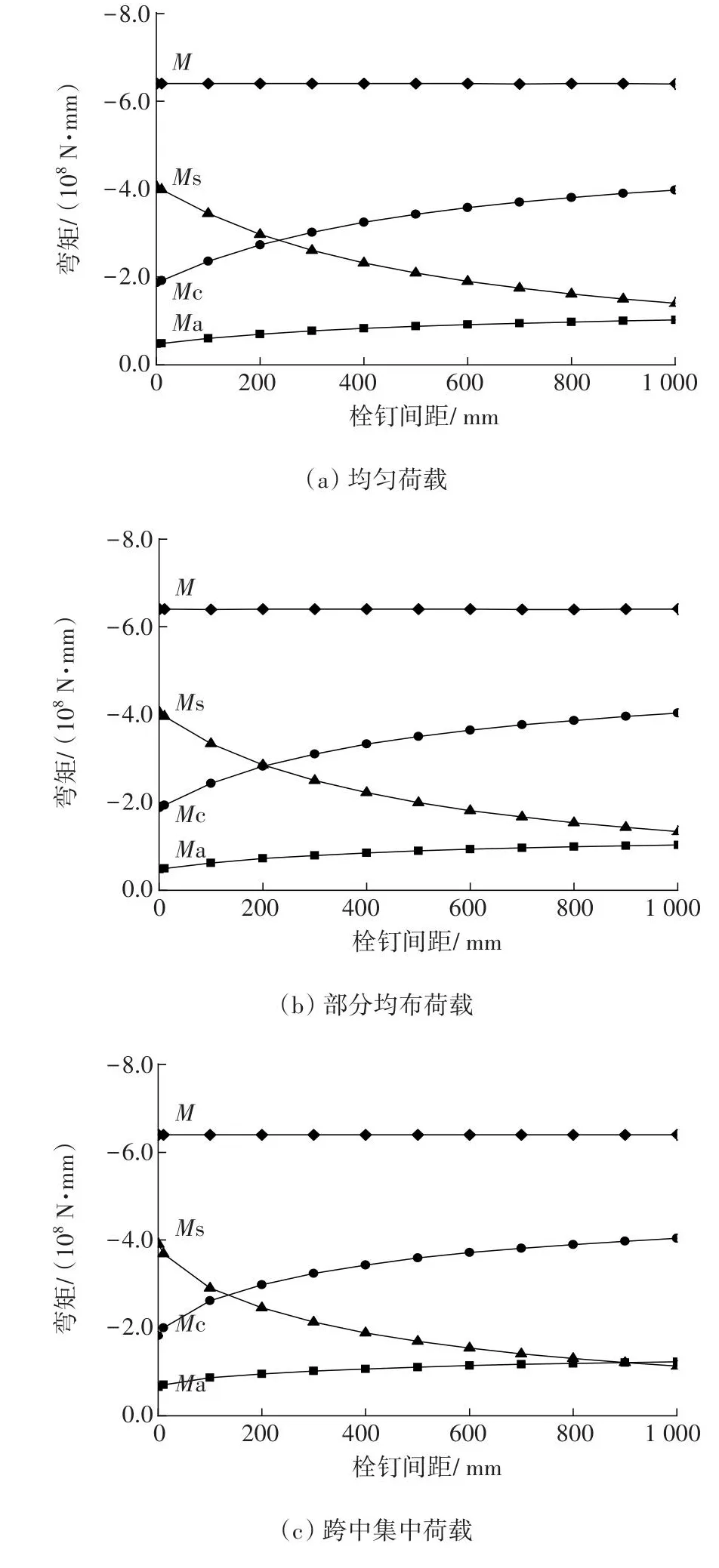
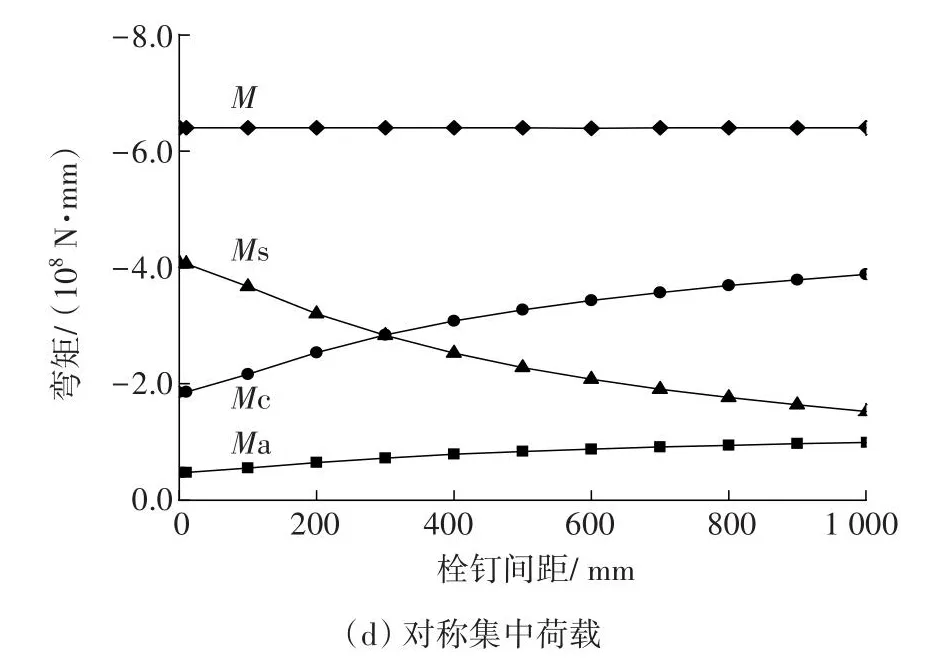
图13 不同荷载、间距下弯矩分布对比Fig.13 Comparison of bending moment changes under different loads and spacing

4 结论

1） 在4种不同荷载工况下，当剪力图面积大小相同时，对称集中荷载所产生的滑移和挠度最大，而跨中集中荷载产生的滑移和挠度最小。

2） 依据滑移图，分段布置栓钉可以有效减小组合梁的滑移及挠度，即便是在跨中部分均匀布置荷载的情况下，跨中挠度也会有所减少。

3） 栓钉间距的减小，意味着同一区段内的栓钉个数的增多，增大了轴力，从而增大组合弯矩，减小了钢梁与混凝土内各自弯矩，从而减小滑移与挠度。

4） 当组合梁栓钉数目足够多时，另一个有效减小组合梁挠度与滑移的方式是通过增设托板、增大d来减小钢梁与混凝土内的弯矩。

5） ANSYS有限元软件在选取正确单元进行组合梁模拟分析时，解与解析解之间非常接近。