突发事件下应急救援物资车辆路径选择方法
2023-09-27陈红文若兰周和平
陈红,文若兰,周和平
(1.长沙理工大学 交通运输工程学院,湖南 长沙 410114;2.衡阳技师学院,湖南 衡阳 421101;3.湖南高速铁路职业技术学院,湖南 衡阳 421002)
近年来,应急救援系统在许多突发事件中发挥了不可替代的作用。在突发事件中,面对紧迫的受灾点物资需求和不确定的路网行程时间,如何科学地调度应急救援物资、选择车辆运输路线是应急救援的关键。许多学者深入研究了应急救援物资车辆调度问题。ALINAGHIAN等[1]考虑动态变化的受灾点需求、位置等要素,构建了应急救援物资车辆的路径选择模型。MARINAKIS等[2]结合了3种自适应策略改进粒子群优化算法,得到优选的配送路径。盛虎宜等[3]综合考虑灾后路网的损毁程度、随机行驶时间等因素,设计了两阶段启发式算法来求解以物资需求点损失最大化和配送时间最小化为目标的应急物资分配-路径选择问题。赵星等[4]考虑受灾点紧急级别、受灾后行程时间变化等因素,以交通量可靠性和路阻函数的行程时间为目标函数来建模,并采用禁忌搜索和非支配排序算法对模型进行了求解。宋英华等[5]结合受灾点人群的年龄分布、伤情严重状况等信息来划分受灾点的受灾严重级别,考虑同一级别的受灾点物资满意度,建立了物资调度模型,并采用经典遗传算法对其进行求解。韩孟宜等[6]设计了结合节约算法、大规模邻域搜索的遗传算法,该算法的速度和结果均优于传统遗传算法的。卢建锋等[7]以运输时间与总环境风险、缺货损失费用最小化为目标函数,构建了多目标的多种类物资调度模型,并设计了NSGAⅡ算法对其进行求解。在求解过程中,先采用锦标赛法进行个体选择,再结合多点交叉算子,加快算法搜索速度,最后采用逼近理想解排序法得到最优解。张文晖[8]考虑多种类应急物资需求,采用拉格朗日松弛算法分解问题,提高了解的收敛速度。石崇玉[9]考虑了不确定的受灾点物资需求,构建多目标车辆调度鲁棒优化模型,确保车辆及时地将应急食品物资配送到各受灾点。许德刚等[10]以行驶时间最小化、需求点的满意度最大化为目标,建立应急调度模型,并提出优化烟花算法对其进行求解,通过改变变异策略、引入禁忌表,提升了算法寻找局部最优解的能力。
这些研究主要集中在应急救援车辆路径问题的模型构建以及求解算法优化两方面。对于应急救援车辆的路径问题,很多学者考虑了受灾点物资需求的不确定性或优先级,对其进行研究[11],还有部分学者考虑到了路段行程时间的不确定性,对其进行研究[12-13]。目前,同时考虑以上两个条件的研究鲜见。因此,本研究基于交通路网区间阻抗,在受灾点需求优先级约束、车辆行驶时间约束等约束条件下,以鲁棒成本最小化为目标,构建应急救援车辆物资配送路径优化模型,并设计Benders分解算法来求解该模型,以便快速、合理地进行多应急物资集散中心的救援与协同调度,以期为应急管理部门的决策制定提供借鉴。
1 问题描述与符号说明
车辆在行驶中会受到交通拥堵、恶劣天气、交通管制等不确定性因素的影响,车辆的行程时间也不会是一个固定值。因此,本研究采用区间来度量交通路网行程时间,该区间内最短与最长行程时间分别对应在道路交通的最好与最差状态下,车辆在该路段上所花费的时间。车辆在该路段上的行程时间可以是处于最长、最短行程时间之间的任意值。本研究以这种方式来表征在实际交通场景中车辆行驶时间的不确定性。
假设在突发事件发生时,交通网络图为G=(N,D),其中,D为路段集,(i,j)∈D,路段(i,j)的行驶时间处于区间阻抗分别是车辆在路段(i,j)最好情况与最差情况下的行程时间,且为节点集,任意节点i∈N;S为应急物资集散中心点集,∀s∈S;M为受灾点集,∀m∈M;K为应急救援车辆集,∀k∈K;E为配送路径方案集,∀e∈E;pi为受灾点i的物资需求量;Tmax为车辆的最长行驶时间。
本研究讨论多个应急物资集散中心车辆的协同调度优化问题,依据灾区实际情境,科学地评估各受灾点的物资需求量,并优先考虑配送需求量大的受灾点。应急救援车辆k从应急物资集散中心s出发,依次给受灾点配送物资,车辆的配送路径为e。在突发事件发生时,需要快速地制定可靠的应急资源调度方案来满足所有受灾点i的物资需求。
2 模型建立
考虑交通路网行程时间的不确定性,建立区间阻抗下应急物资配送路径优化模型,以辅助应急管理部门进行决策,得到最优车辆调度方案。求解此模型的思路为:先寻找出所有符合约束条件的车辆调度方案;再基于该调度方案的情景找到最优调度方案;最后,获得最优调度方案的最大后悔值(鲁棒成本)。该模型旨在找到所有车辆调度方案的最小最大后悔值(最小鲁棒成本),从而最小化决策者的后悔值。
2.1 目标函数与决策变量
以车辆调度方案鲁棒成本最小为目标函数:
式中:为最差情况下车辆在路段的行程时间,即车辆k在路段(i,j)的行程时间取路段(i,j)区间阻抗上界值表示特定情景下路段(i,j)的阻抗,当xkij=1时,式(2)将取到路段(i,j)阻抗的区间上界值tuij;当xkij=0时,式(2)将取到路段(i,j)阻抗的区间下界值tlij。wkij为特定情景下的车辆路径方案。
该模型决策变量为:
其中,wkij为变量xkij基于特定情景下的最佳车辆调度方案;连续变量yikj为路段(i,j)上车辆k的物资载重量;Tik为车辆k行驶到节点i的时刻。
2.2 约束条件
2.2.1 站点约束
每个应急物资集散中心i都能发出与接收多辆车,式(5)表示每个集散中心i最少发出一辆车到受灾点;式(6)表示每个集散中心i最少有一辆车从受灾点返回来;式(7)表示任意受灾点j只由一辆车从一个集散中心出发,为其配送物资;式(8)表示任意车辆k在任意节点j进出流量守恒。
2.2.2 车辆约束
式(9)表示车辆k的行程只能以同一个应急物资集散中心i作为起终点;式(10)表示任意车辆k在任意受灾点j至多服务一次。
2.2.3 边约束
式(11)表示从受灾点i驶向受灾点j的车辆最多有一辆,保证所有受灾点只被一辆车服务。
2.2.4 车辆容量限制约束
式(12)表示从受灾点i驶向受灾点j的车辆k上的物资量ykij要小于车辆额定载量Q;式(13)表示应急救援车辆k在受灾点j卸下了其物资需求量pj,即车辆k在受灾点j前的车内物资量与经过受灾点j后的车内物资量的差值。
2.2.5 时间约束与优先级约束
式(14)表示车辆行驶时间顺序,即若车辆k从受灾点i驶向受灾点j,则该车到达j点的时刻与其到达i点的时刻的差值要小于等于路段(i,j)最大行程时间;式(15)表示受灾点的优先配送权与车辆到达受灾点时刻的关系,即若某受灾点需求越急迫,则其优先配送权就越高,车辆会越早配送物资到该受灾点;式(16)表示车辆k的总行驶时间不能超过最长行驶时间Tmax。
2.2.6 特定情景Xr中的车辆路径wkij方案约束
在特点情景中,路网时间阻抗是确定的,在此确定的阻抗下求解的车辆路径wkij方案,同样要满足车辆路径变量xkij的站点、车辆、优先级等方面的约束。
3 算法设计
应急救援车辆物资配送路径优化模型是容量限制的车辆路径问题。Benders分解算法常用来求解同时包含了0-1整数变量和连续变量的极值问题。其将问题分解为许多小问题来做。其具体思想是采用割平面法,固定复杂变量(0-1整数变量),得到子问题,不断迭代,产生Benders割约束,并将其加入主问题,直至得到最优解。该算法不断迭代,生成新约束条件,故又被称为行生成算法。
在基于阻抗区间的应急救援车辆调度模型中,第一步是确定一个车辆调度方案,第二步是得到基于该方案的特定路网阻抗情景下的最佳车辆调度方案,第三步是通过计算两个方案的总行程时间差值,得到最小鲁棒成本。
3.1 应急救援车辆路径优化模型分解
3.1.1 子模型
随着迭代次数增加,应急车辆调度方案的鲁棒成本逐渐向下界靠拢。
3.1.2 主模型
主模型每被迭代一次, Benders可行性分割约束将被添加一次,使鲁棒成本逐渐向其上界靠拢。当上界值等于下界值时,迭代停止。
3.2 计算步骤
1) 设置模型初始上界值bl为-∞, 初始下界值bu为+∞,路网行程时间取区间阻抗下界值,求解松弛主问题,即得可行方案
3)把wkij代进主模型,新加约束(31),对其进行求解,得到新调度方案xkij、yikj,若Z>bl,则更新bl;
4) 若bl=bu,则输出最优解,停止计算,否则进入5);
5) 令xkij=,返回2),进行迭代,直至bl=bu。
4 算例分析
本研究采用仿真交通路网来测试模型与算法。在该仿真交通路网中,共存在53个节点、125条路段,区间阻抗为图中路段上括号内的数据。其中,设节点1~3为应急物资集散中心,容量限制为3 500 kg; 设节点17~46为受灾点;受灾点物资需求数据见表1,该数据由数值软件MATLAB随机生成,也可根据受灾点特性对受灾点进行需求评估,并且以此为物资配送需求量,配送时将优先配送物资需求量大的受灾点。假定应急物资配送中心有6辆车,每辆车出发时刻均为9∶00,车辆额定载重均为1 500 kg,每辆车的最大行驶时间均限制为45 min,既每辆车总救援时间不超过45 min。
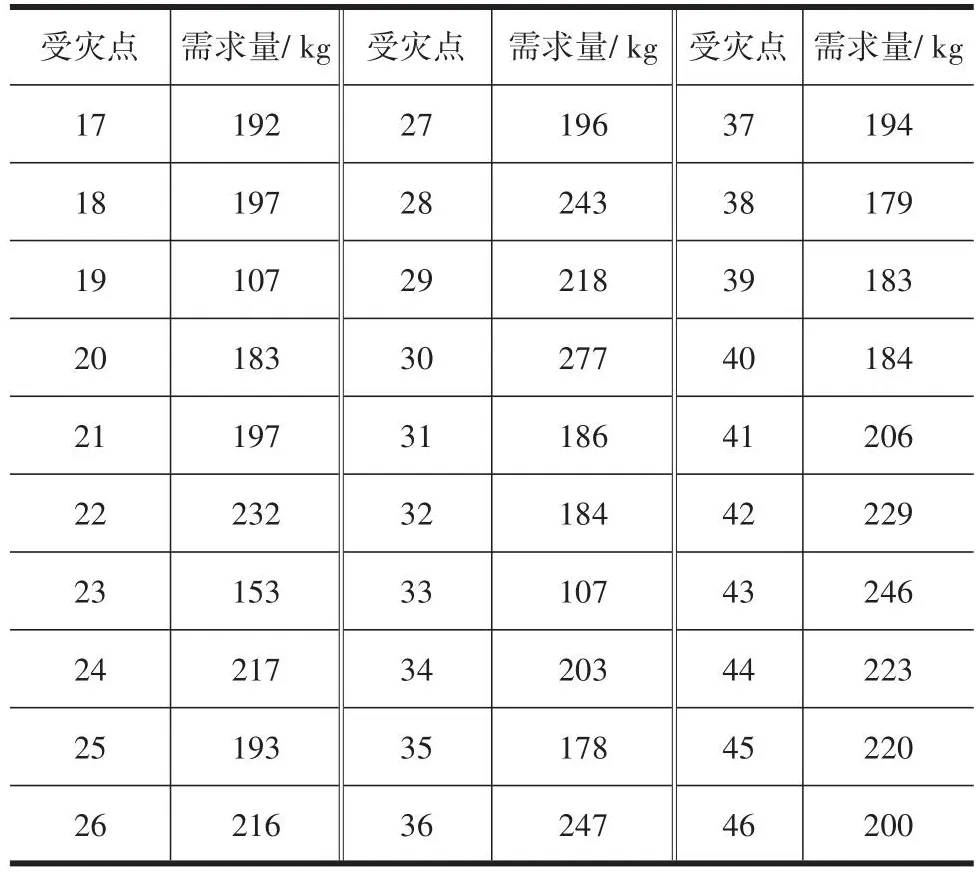
表1 受灾点物资需求数据Table 1 Material demand data
采用AMPL软件,编写应急救援车辆路径优化模型的Benders算法,调用CPLEX对算例进行求解。应急救援车辆路径优化模型迭代了5次,求解时间为0.15 s,总鲁棒成本为93.8,鲁棒车辆调度方案见表2,应急救援车辆物资配送路径图如图1所示,表2中最短路径的括号的点表示该点仅经过但不停留。

图1 物资配送路径图Fig.1 Material distribution route
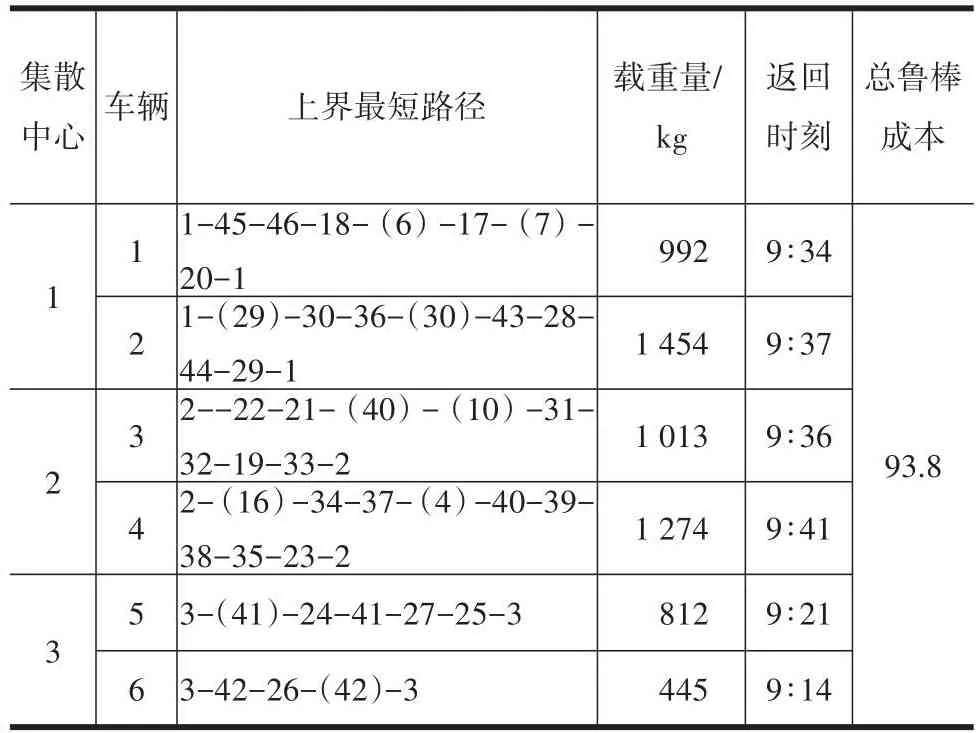
表2 鲁棒车辆调度方案Table 2 Robust vehicle scheduling scheme
从图1可以看出,加粗的车辆路线为车辆调度方案中各应急救援车辆物资配送路径,路段上的区间值表示为车辆在路段上不确定的行程时间。各车辆以应急物资集散中心节点1、2、3为起终点,在不确定的路况下,沿途经过各受灾点进行物资配送,满足每个受灾点的物资需求。
由表2可知,每个应急集散中心均派出了2辆车,所有受灾点物资需求均得到了满足,每辆车的最大行驶时间(总救援时间)均没超过时间限制,如1号集散中心的车辆最大行程时间分别为34、37 min;且满足了受灾点的物资需求量大而优先救援的策略,如45号受灾点的需求量为220 kg,该需求量大于46号的需求量200 kg,故45号受灾点得到了优先配送。本研究得到的配送方案的鲁棒成本更小,行程时间更稳定可靠,可供应急物流决策参考。
5 结论
突发事件发生后的救援具有紧迫性,需要及时地把应急物资从应急物资集散中心配送到受灾点。因此,应急救援车辆调度方案的确定是应急救援的关键。本研究以车辆调度方案最大后悔值最小化为目标,考虑受灾点需求优先级、车辆最大行驶时间、车辆载重量限制等约束条件,基于路段区间阻抗来构建应急救援车辆调度模型,在交通路网阻抗不确定的情况下,保证得到最优的车辆调度方案。通过AMPL软件,采用Benders分解算法对模型进行编程,求解算例。研究结果表明,本模型在满足所有受灾点物资需求的情况下,应急救援车辆路径方案具有较强的稳定性与鲁棒性,可为突发事件下考虑不确定性因素的应急救援调度方案的决策提供借鉴。
