基于极限分析上限法的桩锚支护结构稳定性分析
2023-09-27谭鑫
谭鑫
(株洲市城发集团建设投资有限公司,湖南 株洲 412000)
随着中国经济的高速发展,城市地下空间的利用率越来越高,施工中开挖的基坑变得更深、更大,不得不设立支护结构来保证深基坑的安全。支护结构的设计不仅要保证基坑的稳定性,还需要保证桩自身的稳定性。现有研究[1-2]中对深基坑常见支护结构的设计与施工已有较多讨论,但对于桩锚支护结构的稳定性并没有较深入的研究。故本研究聚焦于桩锚支护结构,拟对其开展自身稳定性的研究。
针对桩锚支护结构稳定性的计算,大多数学者常通过现场工程试验、有限元模拟以及理论分析进行研究。不少学者通过分析工程实际数据,得到相关规律,并展开支护桩的稳定性研究。黄雪峰等[3]结合实际工程,通过现场和试验计算得到悬臂式支护桩的受力特征,并反推出土压力的分布规律。韩健勇等[4]通过分析现场实测数据,计算了支护结构的内力,并验算了基坑的整体稳定性。在有限元模拟方面,刘自由[5]研究了锚杆对基坑变形的影响,利用FLAC3D建立了应变软化模型,发现锚杆长度与支护桩所承受压力之间的关系。赵杰等[6]采用数值模拟分析了预应力锚杆复合土钉支护体系各因素对基坑稳定性的影响。韩建勇等[7]基于杆系有限元法,对桩锚支护结构进行内力计算,得到了基坑支护的变形规律。这些学者通过数值模拟,分析了影响桩锚支护体系稳定性的因素,并对基坑的稳定性进行了相关研究。通过工程试验以及有限元模拟,研究了支护桩的稳定性,为相关理论研究提供了参考。
针对桩锚支护结构桩身受力以及稳定性的理论研究,年廷凯等[8-9]应用极限分析下限法,得到了综合被动土压力和主动土压力的系数,并通过计算得到桩周土体侧向容许承载力和弹性桩锚固深度公式,确定了桩锚支护结构的嵌固段深度。秦会来等[10]基于极限分析上限理论,构建相容速度场,得到了预留土支护基坑被动区极限抗力的上限解。梁冠亭等[11]应用 Morgenstern-Price法,对桩锚结构支护边坡模型进行稳定性分析,并认为桩锚结构设置在边坡的中部时,边坡的整体稳定性最好。刘杰[12]基于极限分析上限法,将桩土视作整体,采用能量估算法,得出桩土的整体稳定性,并应用数值模拟进行验算。这些学者通过不同的理论方法计算桩锚支护结构稳定性,但均只考虑了桩本身与土的作用关系,没有考虑锚索对支护结构稳定性的影响,这显然是不合理的。
因此,本研究基于极限分析上限理论,将桩土视作整体,锚索视作外力,拟考虑土体分层、黏聚力和填土与桩锚支护结构的桩身、桩底的摩擦作用等因素的影响,求出外力做功和内能耗散功率,应用能量估算法推导出桩锚支护结构稳定性系数的计算公式,以期对相关工程提供参考。
1 理论模型
1.1 基本假设
考虑到桩锚支护结构的工程特性,为便于计算,作以下基本假定:
1) 桩土系统无限长,并考虑为密桩情况,不考虑桩的相互作用,近似看成桩锚支护结构;
2) 桩前、后填土面水平,桩后填土与桩顶面同高,均为层状黏土;
3) 桩前填土、桩后填土的破裂面为折线面,并用朗肯破裂角进行近似计算;
4) 填土满足Mohr–Coulomb破坏准则和极限分析上限理论的基本假设,符合相关流动性法则;
5) 假设桩为刚性桩,土体破裂面为通过墙踵的斜直线形破裂面。
桩土系统如图1所示。桩土系统包含:桩后填土破裂区、桩前填土破裂区和支护桩。主、被动区域填土高度H1、H2可分别表示为:
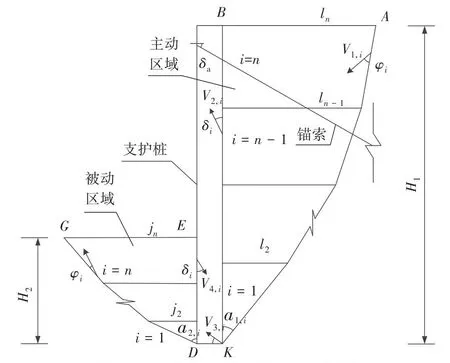
图1 桩锚支护结构稳定性理论模型Fig.1 Stability theory model of pile-anchor retaining structure
式中:H1,i、H2,i分别为主动填土i区域和被动填土i区域的高。
将填土沿深度方向均分成n层,假设填土表面水平,主被动区填土宽度分别为AB、EG。ln为主动区分层土上顶面宽度;jn为被动区分层土上顶面宽度;γi为填土重度;D为桩的直径;V1,i为主动填土区运动速度;与滑裂面的夹角φi为土体内摩擦角;V2,i为主动区的填土与支护桩相对运动速度;δi为支护桩与填土的界面摩擦角;支护桩底面为速度间断面;V3,i为支护桩的运动速度;δb为桩底面摩擦角;V4,i为被动区的填土与支护桩相对运动速度;V5,i为被动填土区运动速度;δa为锚索与水平面夹角;L为锚索水平间距;90°-α1,i为主动区破裂角;90°-α2,i为被动区破裂角。
由图1所示的几何关系,求出其余各边长:
根据极限分析上限法[13],相邻块体之间的速度V1、V2、V3和V3、V4、V5均需满足速度相容关系,其几何关系如图2所示。
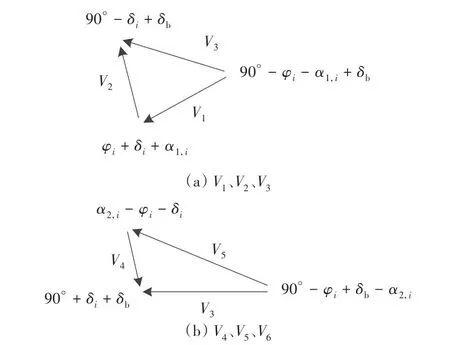
图2 相邻块体速度相容场Fig.2 Speed compatibility field
速度矢量关系:
由图2、式(3)~(4)以及三角形正弦定理可以得到支护桩运动速度V3与V1,i、V2,i、V4,i、V5,i之间的关系:
1.2 桩土系统能耗计算
根据极限分析上限法对桩土系统的外力做功,计算内能耗散。
1) 桩后填土ABK区重力g1做功Wg,1。
桩锚支护结构稳定性理论模型如图1所示,重力g1,i与速度V1,i的夹角为α1,i+φ1,i,则有:
2) 桩前填土GED区重力g2做功Wg,2。
由重力g2,i与速度V5,i的夹角为π-α2,i+φi,可得:
3) 桩锚支护结构重力g2做功Wg,3。
由重力g3与速度V3的夹角为90°+δb,可得:
其中,S为桩截面面积,为面积换算成正方形时的边长长度。
4) 桩土界面BK能量耗散D1。
C1是BK界面总黏聚力,C1与V2,i的夹角为δi,ci为桩土界面的抗剪强度指标,则有:
5) 桩土界面ED能量耗散D2。
C2为ED界面总黏聚力,C2与V4,i的夹角为δi,ci为土的抗剪强度指标,则有:
6) 桩后填土倾斜界面AK的能量耗散D3。
C3为AK界面总黏聚力,C3与V1,i的夹角为ϕi,ci为土的抗剪强度指标,则有:
7) 桩前填土倾斜界面GD能量耗散D4。
C4为GD界面总黏聚力,C4与V5,i的夹角为φi,ci为桩土界面的抗剪强度指标,则有:
8) 桩底界面能量耗散D5。
C5为桩底界面总黏聚力,与V3的夹角为δb,cn为桩土界面的抗剪强度指标,则有:
9) 锚索拉力做功D6。
水平分力与V2的夹角为90° +δ,竖直分力与V3的夹角为90° +δb,L为锚索水平间距,则有:
10) 能量平衡方程。
1.3 支护桩稳定系数
基于能量法得到桩锚支护结构稳定系数Fs,其表达式为:
式中:ΣWn为所有外力做负功的功率;ΣD为总内能耗散率;ΣWP为所有外力做正功的功率。
当Fs=1时,系统处于极限平衡状态。为简化计算,采用郎金土压力理论的破裂角进行计算,即主动土压力破裂角为45° +φi/2,被动土压力破裂角为45° -φi/2。
2 计算方法合理性验证
为评定本研究计算方法的合理性,依托工程实例,计算桩锚支护结构的稳定性系数,并将所得结果与目前较为主流的规范计算结果作对比,验证该方法的合理性。
以株洲火车站东广场综合交通枢纽一期工程为例,其位于株洲城市中心区,据钻孔揭露及工程地质调查成果,结合区域地质资料,得到测区上部为第四系覆盖层,下部为白垩系戴家坪组泥质粉砂岩的结论,各土层物理具体参数见表1。该工程为基坑围护工程,并采用了桩锚支护结构对其进行稳定支护,桩锚支护结构简图如图3所示。

表1 土层物理力学参数Table 1 Physical and mechanical parameters of soils
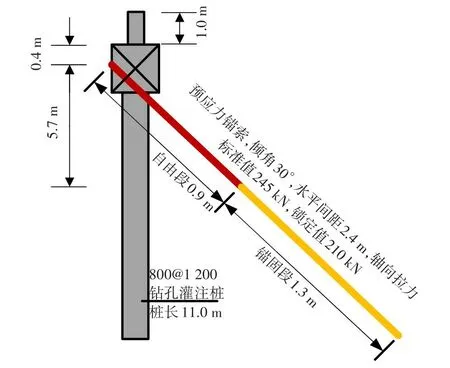
图3 桩锚支护结构支护示意Fig.3 Sketch of anchor pile retaining
应用本文方法,取H1为11.0 m,H2为5.5 m,γq为25 kN/m3,D为1.2 m,L为2.4 m,主动土压力破裂角为45°+φi/2,被动土压力破裂角为45°-φi/2,并充分考虑墙后不同深度土体的物理参数,通过该理论计算得到桩锚支护结构的稳定系数Fs为3.591 1。
依据《建筑基坑支护技术规程》(JGJ 120—2012),可得Fs,1=3.189 6,该值与计算结果较为接近,这二者均认为该桩锚支护结构稳定性满足要求,可见本计算方法的合理性。
3 参数分析
为探讨不同参数对桩锚支护结构稳定性的影响,通过改变锚固力F、桩径D以及嵌固段长度H2的取值,分析各参数与桩锚支护结构稳定性Fs的关系,并分析该工程实例。
3.1 不同水平间距下锚固力F对稳定性系数Fs的影响
取水平间距L分别为1.0、1.5、2.0、2.5 m,同时改变锚固力F的取值,其他条件保持不变,得到水平间距L不同时稳定性系数Fs和锚固力F的关系,如图4所示。
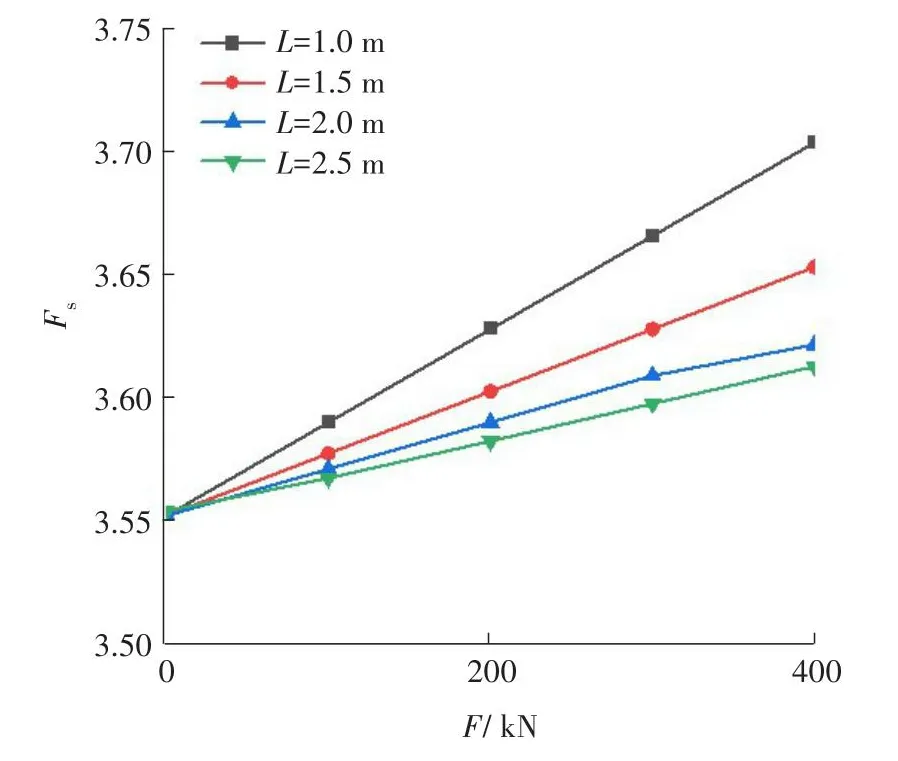
图4 Fs - F关系Fig.4 Relationship between Fs and F
从图4可以看出,当水平间距相同时,二者间近似呈线性关系,稳定性系数Fs随锚固力F增大而增大,且水平间距越小,增长速率越快;在相同锚固力F的作用下,稳定性系数Fs随水平间距的增大而减小,同时减小幅度随着水平间距的增大而减小。
3.2 桩径D对稳定性系数Fs的影响
桩径D分别为0.8、1.0 、1.2 、1.4 、1.6 m,其余条件不变,计算稳定性系数Fs,可得到Fs与D的关系,如图5所示。从图5可以看出,稳定性系数Fs与直径D近似呈线性关系,且Fs随D的增大而增大。每增加0.2 m的直径,稳定性系数大致增长0.03,表明增大直径是提升桩锚支护结构稳定性的方式之一。

图5 Fs-D关系Fig.5 Relationship between Fs and D
3.3 嵌固段长度H2对稳定性系数Fs的影响
桩锚支护结构嵌固段H2的长度分别为10、11、12、13、14 m,其余条件不变,得到Fs与H2的关系,如图6所示。从图6可以看出,当其他参数不变时,随着嵌固段H2增大,稳定性系数Fs随之增大,但增大的速率逐渐减小。每增大1 m的嵌固段长度,稳定性系数约提高0.3。这表明嵌固段长度H2对稳定性系数Fs的影响比较明显。因此,在工程实例中,可适当增大嵌固段的埋深,可保证桩锚支护结构的稳定性。
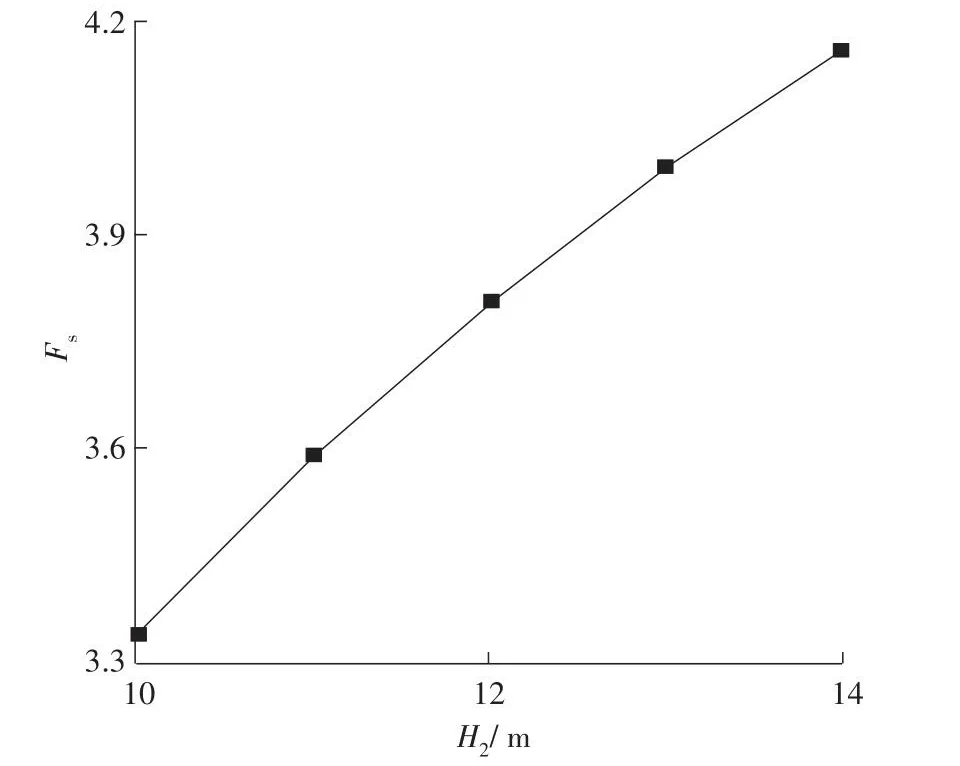
图6 Fs -H2关系Fig.6 Relationship between Fs and H2
4 结论
1) 以株洲火车站东广场综合交通枢纽一期工程为背景,考虑土的分层、土体黏聚力、锚索拉力和简化的土体与桩锚支护结构桩身、桩底的摩擦作用,应用极限分析上限法,得到了桩锚支护结构稳定性计算公式。
2) 将本方法应用于工程实例,得到的稳定性系数与建筑基坑支护技术规程[12]的稳定性计算结果接近,验证了本文方法的合理性。
3) 由参数分析的结果,得出随着直径、嵌固段长度的增大或锚固力的增大,水平间距的减小,桩锚支护结构稳定性系数逐渐增大的结论。
