谈单元整合教学在小学数学中的应用

潘良海

［摘  要］ 传统的逐课教学有时会影响单元教学目标的实现以及学生完整认知体系的建构。研究者以“两位数乘两位数”单元教学为例，通过对教材内容的整合和拓展，形成了完整的整数乘法知识结构，不仅提升了教学效率，还发展了学生学习能力。

［关键词］ 逐课教学；整合；拓展

数学知识的学习遵循由低到高、由易到难的逻辑顺序，前面的知识往往是后面知识的基础和前提。因此，对数学知识的教学不能仅停留于本节内容，教师应该着眼于本单元、本学期甚至整个小学段，用全局的眼光去思考，用整体的思路去建构教学体系，从而培养学生良好的学习习惯和学习品质，提升学生的数学核心素养。笔者在教学“两位数乘两位数”时，从单元整合思路出发，将新知与旧知进行串联，引导学生探究整数运算的秘密。

一、教学分析

1. 内容分析

“两位数乘两位数”是整数乘法的重要组成部分，这部分内容既与前面所学的多位数乘一位数有密切的联系，又为后面学习多位乘法做好了铺垫，还是除数是两位数的除法运算的思维基础。

在本单元教学中，大多数教师习惯按照教材顺序分五步教学：第一步，学习乘数是整十数乘法的口算；第二步，学习两位数乘两位数的口算；第三步，学习两位数乘两位数不进位的笔算；第四步，学习两位数乘两位数的进位笔算；第五步，进行练习巩固。

教学内容由易到难地逐层深入，顺应了学生的思维发展。但是纵观以上内容不难发现，这样的教学安排不利于结构化教学的实施，不利于学生整体认知体系的建构。其实，第一步内容对于学生来讲并不难，学生完全可以将“十位数乘一位数”的方法进行迁移，自主完成该部分内容的学习。无论是从结构化教学的角度来分析，还是从教学重难点来考量，在本单元教学中教师有必要將该部分内容进行整合，将散落于不同年级的知识点进行串联，打通知识方法间的联系，从而有效提升学生的知识迁移能力，提高教学效率。

2. 学情分析

在学习本章内容前，学生已有了多位数乘一位数的运算经验。笔者结合课前导学发现，大部分学生已经能够独立完成整十数乘法以及两位数乘两位数的口算。不过大多数学生在运算时主要依靠模仿，对具体的算理并不明晰，并且学生欠缺笔算的经验。

结合学生反馈不难发现，本单元教学的难点为两位数乘两位数的笔算。教师若想帮助学生突破难点，则应该让学生明晰算理，让学生知晓每次运算后积的表征和明确积的定位；同时，通过对比分析、方法类推等教学，帮助学生形成完善的认知。

二、课时安排

基于以上分析，在单元教学中，笔者将教学内容进行了重组和拓展。

第一课：将教材中的前三课内容进行整合，归结为“两位数乘两位数的笔算（不进位）”；

第二课：在第一课的基础上安排1节拓展课，让学生追随古人的思路去探寻蕴含其中的算理，完成知识的传承和内容的深化；

第三课：完成“两位数乘两位数的笔算（进位）”。有了前面的铺垫，学生在学习进位乘法时能够信手拈来；

第四课：进行综合练习，完成知识的巩固和认知体系的建构。

通过这样的整合和拓展，笔者将原来的5节课缩减成4节课，不仅提高了教学的效率，而且凸显了教学重难点，有助于学生提升学习能力。

三、重点课例设计与实践

1. 整合课

（1）教学目标

掌握笔算方法，明晰算理，能够正确地完成运算；借助具体应用，感悟运算价值，形成愉悦的学习情感。

（2）教学过程

环节1：情境引入，认识算理

师：昨天老师请你们帮的忙，你们还记得吗？

生（齐声答）：记得。

师：很好，我们先回顾一下问题。（教师PPT出示问题）

问题1： 某校队列表演团招募学员，队列比赛要求每行有14人，共12行，你知道需要招募多少学员吗？

师：说一说，你们是如何解决这个问题的？

生1：可以用画图法，简捷、直观。

师：你是如何画的呢？

生1：这个很简单，如图1。（教师展示图1）

师：这是一个办法，不过这样一个一个地画需要很长的时间，还有没有其他的画法呢？

（教师选择了两个有代表性的画法进行展示，如图2和图3）

师：这几幅图你们看懂了吗？

生2：其实这3张图所要表达的意思是相同的，就是把12个14加起来。

师：很好，通过一个一个地相加算出最终的结果为168。虽然我们通过以上过程得到了答案，但是却花费了较多的时间。从时间成本的角度来思考，以上过程如何优化呢？

生3：可以用乘法来运算，算式为14×12，不过这个我们好像还没有学。

师：没有学过是不是就不能算了呢？

生4：我会算。（教师让学生板演运算过程）

14×12=14×2×6=168（人）

在生4的启发下，学生给出了不同的运算过程。比如，14×12=14×3×4=168（人），14×12=14×（2+10）=14×2+14×10=28+140=168等。通过拆分12，学生将问题转化为自身熟悉的“两位数乘一位数”的运算问题。

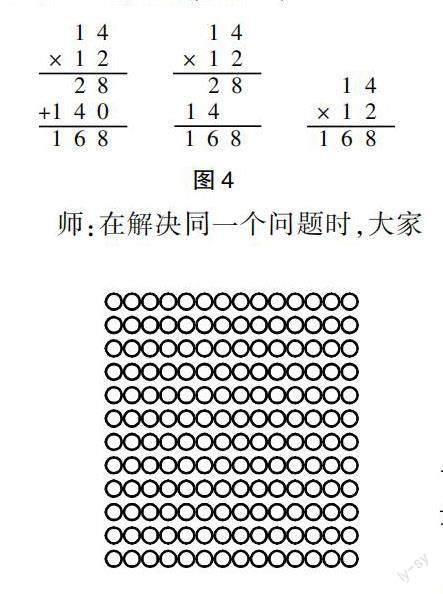
师：刚刚老师巡视发现，还有学生利用竖式法完成了运算。（教师展示学生运算结果，如图4）

师：在解决同一个问题时，大家用了不同的方法，比如画图法、口算法、竖式法等。在同一种方法中大家给出了不同的表现形式，为了便于大家理解，现在我将大家解决问题的方法重新组合（如图5），你有什么发现？

设计意图：环节1的教学充分调动了学生元认知。在探究环节教师预留充足的时间让学生展示，并通过对比分析，沟通了不同方法之间的联系，为学生更好地理解算理做好了铺垫。

环节2：沟通联系，理解算理

师：对比以上三种不同的运算方法，你有什么发现？谁来说一说？（很多学生已经发现了蕴含其中的秘密，都跃跃欲试）

生5：它们的实质是一样的。口算中的14×2，其与竖式中的第一步相对应，就是图1中的前2行；口算中的14×10，其与竖式中的第二步相对应，就是图1中剩下的10行；28＋140＝168，就是竖式的最后一步，代表图1中的12行。

师：你们认可生5的说法吗？（生点头表示赞成）

师：说得很好，竖式中的28是14与12中的个位2相乘得到的，就是口算中的第一步，图1中的前两行。谁来说一说竖式中的140是怎么得到的？168呢？

生6：竖式中的140是14与12中的十位1相乘得到的，就是口算中的14×10，对应图1中的10个14。

生7：168就是12个14。

师：你们太棒了，找到了不同方法间的联系，理解了运算的实质。

设计意图：通过对比分析，不仅让学生看懂了竖式运算，而且明晰了竖式运算的本质，深刻理解了算理。学生经历的上述运算过程为其能够自主完成“三位数与两位数相乘”或“多位数与两位数相乘”的运算奠基。

环节3：对比分析，深化理解

师：在刚刚的竖式运算中，有的学生是这样写的，你们看懂了吗？（教师再次给出刚才的竖式运算过程，如图6）

生8：先算14×2=28，再算14×1=14，最后算28与140的和。

师：140中的0去哪里了呢？

生9：因为8+0=8，所以就省略了。

师：省略后的14，其代表的意义有没有发生变化呢？

生10：没有变，去掉0后，4是与28中的十位2对齐的，而1是写在百位的，所以依然表示14个10。

师：很好！那么这里的“+”是否能省略呢？（生争辩）

师：大家都说得很好，虽然省略了“+”，但是还是运算的两个数的和。为了追求简捷，竖式中的“＋”和“0”可以省略不写。（教师及时点评）

生11：那么是不是这样写也可以呢？（生给出自己的运算过程，如图7）

图7

师：你们怎么看？

生12：这个虽然简单明了，但是缺少运算过程，应该不行。

师：说得很好，在运算时可以追求简捷，不过运算过程要交代清楚。

设计意图：通过对比分析明确竖式运算过程的书写规范，培养学生思维的严谨性。在作业和测试中笔者发现，有些学生因为盲目追求效率而“偷工减料”，常常因运算过程缺失而导致运算错误。小学阶段正是培养学生学习习惯和思维习惯的黄金期，因此在教学中教师应关注细节，培养学生正确的学习观。

环节4：巩固练习，类推笔算方法

师：大家思考一下，以下几个问题你能用竖式运算吗？（教师用PPT给出问题）

①23×13；②32×21；③132×21。

从练习反馈来看，大多数学生顺利完成了前面两个问题的运算，问题③也有很多学生做对了。为了巩固算法，教师对运算过程进行了小结：在竖式运算时，需要注意每次“积”的书写位置。若用个位去乘，则积的末尾写在个位；若与十位相乘，则积的末尾写在十位。

师：这三个问题大家都完成得非常好，前面两个问题已经重点学习了，这里就不再重复。不过问题③为“三位数乘两位数”，这个我们并没有学习过，你们是怎么进行计算的呢？

生13：其实这个与前面的问题差不多，先是132×1=132，然后是132×20=2640，最后是132＋2640=2772。

师：说得很好，其实它的运算与“两位数乘两位数”的本质是相同的。先算出1个132，再算出20个132，然后将两个结果相加就是21个132了。

师：今天所学的竖式运算，大家有没有一种似曾相识的感觉呢？

生（齐声答）：有。

师：与我们以前学习的什么内容类似呢？

生14：与我们前面学习的“乘数是一位数的乘法”类似。

师：很好，大家猜想一下，我们接下来可能会学到什么呢？

设计意图：借助问题既沟通了旧知，又引导学生尝试探究新问题，为探究后面的问题奠定坚实的基础。

在整个教学过程中看似没有提及“乘数是整十数乘法”，其实它已经蕴含于笔算教学中，比如14×10、132×20。将学生触手可及的问题进行整合，不仅可以帮助学生规避机械运算所带来的枯燥感，而且有助于学生建立结构化认知体系。

2. 拓展课

（1）教学目标

进一步了解竖式的不同表示方法，拓展学生的知识面；强化不同方法间的联系，建构认知体系；感悟数学发展史，激发学生的数学学习兴趣，发展学生的数感。

（2）教学过程

环节1：复习引入（略）

该环节教师先给出练习让学生独立完成运算，然后与学生共同回顾了算理。

环节2：对比中沟通，拓宽学生视野

师：其实，古代的豎式运算并不是现在这样的。你们想不想知道古人如何表示竖式运算？竖式又是如何演变的呢？（听说古代的竖式不是现在这个样子，学生都迫不及待地想看一下它的样子，学习积极性被激发出来）

师：很好，我们以14×12为例，看看古人如何运算。

①视窗法

师：思考一下，这个算法你看得懂吗？（教师用PPT给出运算过程，如图8）

生1：4×2=8，10×2=20，4×10=40，10×10=100。

师：很好，与我们所用的竖式法相比，你感觉哪个更方便、更快捷呢？（学生一致认同现在的方法更方便）

②画线法

师：观察图9，你又有什么发现呢？（教师预留时间让学生画一画、圈一圈）

生2：如图10，只要看这些交点就可以了，百位上1个点代表100，十位上6个点代表60，个位上8个点代表8。

师：怎么算出来的呢？

生3：10×10=100，10×4=40，10×2=20，2×4=8。

师：大家真是太厉害了，不仅发现了画线的秘密，而且还知道它所表达的意义。

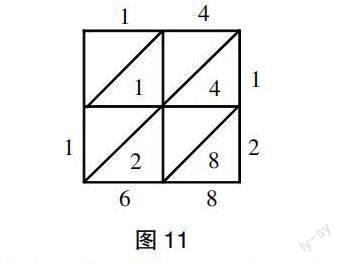
③表格法

师：现在用你们的“火眼金睛”看一看，你知道表格中蕴含了什么秘密吗？（师给出图11）

图11

生4：表格里的数分别为：2×4=8，2×1=2，1×4=4，1×1=1。

生5：与画线法类似，这里面也有个位、十位和百位。

生6：这样斜线上的数加起来，可以得到168。

师：大家真厉害，不仅给出了答案，而且还发现了古人方法里关于数位顺序表的秘密。

师：观察表格容易发现，里面还有一些空格子，你们猜一猜，这个又会蕴含着什么秘密呢？（生沉思）

师：这个问题在下节课的学习中就会揭晓。（为进位乘法做铺垫）

与前面探究过程相似，接下来教师通过对比沟通，引导学生寻找隐藏于不同形式中的联系，最终发现无论哪种运算都有28和140的身影，只是它们的记录方式不同，其蕴含的运算原理是相同的。

教师组织学生尝试用不同的方式运算23×13、32×21、132×21，通过对比让学生体会现代竖式运算的优越性。虽然拓展课中所讲述的古人运用的运算方法现在已经不再使用，但是其在拓展学生知识面、培养学生数感、发展学生思维能力和探究能力等方面的价值不可估量。

总之，用好教材并不是完全按照教材的编排顺序进行知识的讲授，而是应结合单元结构及具体学情对教材进行拆分和重组。