面向异构多背包问题的多级二进制帝国竞争算法

李 斌，唐志斌

（1.福建理工大学 机械与汽车工程学院，福州 350118；2.福建省大数据挖掘与应用技术重点实验室（福建理工大学），福州 350118；3.福建理工大学 交通运输学院，福州 350118）

0 引言

背包问题（Knapsack Problem，KP）［1］是一类经典的组合优化问题，也是典型的NP-hard 问题［2］。该类问题有诸多变种，如0-1 背包问题、完全背包问题、多维背包问题［3-4］、多重背包问题［5］、其他变种背包问题［6-7］等。其中，0-1KP 是最基础的背包问题。现实中很多问题都被拟合成背包问题进行研究，如货物装载问题、资源分配问题、电网维护检修问题、投资决策问题等。

穷举法、动态规划法［8］等传统精确算法能准确得出背包问题的最优解，但是随着物品数量和背包容量的增加，算法的时间复杂度成指数上升，难以得到最优解或需要远超期望的时间才能获取最优解，表现出计算效率低、对硬件设备要求高的特点。因此，传统精确算法大部分情况下只适合求解小规模背包问题。元启发式算法作为近似精确算法，已成为近几年研究背包问题的主流方法。目前，差分进化（Differential Evolution，DE）算法［9］、遗传算法［10］、粒子群优化（Particle Swarm Optimization，PSO）算法［11］、狼群算法［12］、狮群算法［13］、鲸鱼优化算法［14］都已成功应用于优化求解背包问题。帝国竞争算法（Imperialist Competitive Algorithm，ICA）［15］是基于群体智能的元启发式算法，它独特的演化原理使算法在前期具有一定的全局勘探能力，在后期具有较强的局部挖掘能力。背包问题的求解难度主要在于从次理想解到理想解的过程，这个过程需要不断在当前解的周围空间作寻优尝试。因此，相较于遗传算法、DE、PSO 等元启发式算法，后期具有较强局部寻优能力的ICA 存在一定优势；也正因为ICA独特的演化原理，它也容易因过快收敛而陷入局部最优。

本文基于ICA 的不足和KP 的特点，提出求解0-1KP 的二进制帝国竞争算法（Binary Imperialist Competitive Algorithm，BICA）。BICA 基于标准ICA，通过离散化方法成功获得求解KP 的能力，并引入双点自变异算子和跳出局部最优算法（Jump out of Local Optimum Algorithm，JLOA）增强算法性能，算法在寻优过程产生的新解将通过改进后的修复优化机制处理。大量实验表明BICA 在求解0-1KP 时具有较强的性能，表现为寻优精度高、算法稳定性好、求解效率高，能作为有效求解大规模0-1KP 的新方法。此外，本文从典型物流服务场景中共性抽象出一种新KP 变种-异构多背包问题（Heterogeneous Multiple Knapsack Problem，HMKP）。为有效处理HMKP，将BICA 种群结构改进为一种多级算法结构，提出求解HMKP 的多级二进制帝国竞争算法（Multiple Level Binary Imperialist Competitive Algorithm，MLB-ICA），相关算例实验表明，MLB-ICA 能有效求解HMKP。本文的研究不仅为0-1KP 的求解提供有效的新方法，还尝试探索了KP 新变种问题，且提供了一种针对性的群集智能算法解决方案。

1 问题描述

1.1 0-1背包问题描述

0-1KP 可以描述为：有n件物品和一个容量为C的背包，第（ii={1，2，…，n}）件物品的重量属性为wi，价值属性为pi，从n件物品中选择部分物品放入背包，使得在背包容量限制下背包内所有物品总价值V最大化。定义物品装入方案为[x1，x2，…，xi，…，xn](xi={0，1})，xi=1 表示第i件物品放入背包；xi=0 表示第i件物品不放入背包。0-1KP 的数学表达式为：

0-1KP 是典型的基于约束条件的离散最大化问题，对于违反约束条件的物品装入方案，有罚函数法［16］和修复法［17-18］对不可行方案进行可行化处理。罚函数法和修复法都有操作简单的特点，但惩罚函数的设计却没有统一的标准来借鉴，怎样设计一个合理的惩罚函数仍然是一个难题。修复法在现有研究中更常见，分为修复和修正两个操作：修复操作将不可行解处理为可行解；修正操作在约束条件下对当前方案进一步优化。修复法的描述如算法1 所示。

算法1 修复法。

输入X，H1，H2，W；

其中：X是待处理解；H1、H2是分别按照价值密度升序、降序排列的物品索引列表；W是当前背包内物品总重量；X'是经修复法处理后的可行解［19］。

元启发式算法能在可接受时间内求解大规模0-1KP 问题，而这是传统精确算法的不足。处理0-1KP 的元启发式算法可分为两类：第一类是以遗传算法［18］、禁忌搜索算法［20］为代表的可直接通过0-1 编码方式求解问题的算法；第二类是以DE 算法［21］、ICA 为代表的不可直接0-1 编码的连续域群集智能算法。第二类算法提出于连续域相关问题的研究中，可借助编码转换方式将实数编码转换为二进制0-1 编码以求解0-1KP，该过程不可避免地会增加算法计算复杂度，但连续域上的搜索空间相对更精细，基于种群的连续域算法有更多机会直接找到最优理想解。BICA 分别引入两种已被广泛使用和被证明有效的编码转换函数帮助ICA 间接求解0-1KP，并在后续实验中研究了两种编码转换函数对算法性能的影响。

1.2 多背包问题描述

多背包问题（Multiple Knapsack Problem，MKP）［22］可描述为：有n件物品和m个容量属性为Cj(j=1，2，…，m)的背包，第（ii={1，2，…，n}）件物品的重量属性为wi，价值属性为pi，从n件物品中选择部分物品放入m个背包中，在各个背包容量约束下，使所有背包中的所有物品总价值V最大化。定义背包内物品装入方案为[x1，x2，…，xi，…，xn] (xi=[xi1，xi2，…，xij，…，xim]，i=1，2，…，n，j=1，2，…，m)，其 中，xij=1 表示第i件物品放入第j个背包；xij=0 表示第i件物品不放入第j个背包。MKP 的数学表达式为：

MKP 中物品可选择的背包不唯一，利用传统精确算法求解MKP 的计算复杂度将成指数级增长，远高于求解0-1KP 时的计算复杂度，元启发式算法因此成为研究MKP 的首选。元启发式算法求解MKP 需确定个体解的编码方式，现有研究中常用编码方式有整数编码［23］、m×n阶0-1 矩阵编码［24］，前者因编码方式简单且具有更低计算复杂度而更受偏好。

1.3 异构多背包问题描述

异构多背包问题（Heterogeneous Multiple Knapsack Problem，HMKP）是多背包问题的一种特殊形式，不可以简单看作多个0-1KP 的再组合优化问题。HMKP 是从离散组合优化的角度从多个典型的物流服务场景共性抽象而来，是多个复杂物流系统的计划调度问题原型。该问题的提出和建立，能更好地处理物流行业中的控制决策问题［25］。基于复杂物流服务场景，HMKP 的求解架构如图1 所示。

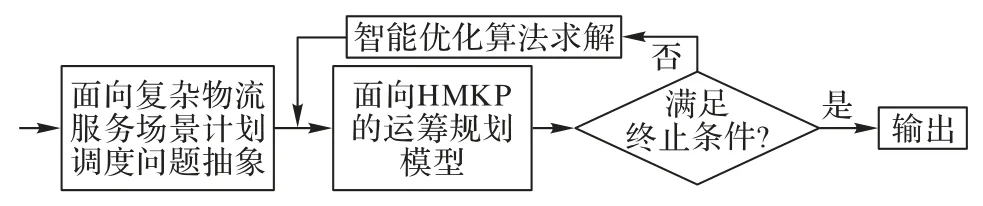
图1 HMKP的求解架构Fig.1 HMKP solution architecture

相较于MKP，HMKP 中部分或全部物品对待放入的背包有指定要求，它的求解因此更复杂。作为MKP 特殊形式的HMKP，它的求解算法的编码方式可选择整数编码或0-1 二进制编码，但是这两种编码方式在算法的演化过程中不可避免地需要限制个体解编码串上部分基位的取值，以满足这部分基位所代表的物品对分配背包的要求。

MLB-ICA 从算法设计上入手，先给所有物品都分配一个满足它的需求的背包，接着利用BICA 并行求解各部分的最优配置方案，后续在物品对背包约束条件下变换各物品被分配的背包，循环演进。

HMKP 可以描述为：有m堆物品，对应每堆物品的数量分别为{n1，n2，…，nm}，有m个背包，背包的容量属性为Cj(j=1，2，…，m)，每堆物品对应一个背包，且只能选择放入或者不放入该背包，不能放入其他背包中，第j堆物品中的第i件物品的重量属性为wji，价值属性为pji，从每堆物品中选择部分物品放入相对应的背包中，使所有背包中的所有物品总价值V最大化。定义背包内物品装入方案为[x1，x2，…，xj，…，xm] (xj=[xj1，xj2，…，xji，…，xjnj]；xji={0，1}，i=1，2，…，nj；j=1，2，…，m)，xji=1 表示第j堆物品中的第i件物品放入第j个背包，xji=0 表示第j堆物品中的第i件物品不放入第j个背包。HMKP 的数学表达式为：

本文描述的HMKP 是一个基础原型问题，当面临具体实际问题时，可以允许部分物品有选择装入背包的权利，本文的研究对于未来HMKP 的扩展有一定的借鉴意义。

2 求解0-1KP的二进制帝国竞争算法

在设计改进算法求解0-1KP 时，本文充分考虑了问题特点和算法的不足，提出了二进制帝国竞争算法（BICA）。在算法的运行过程中，修复优化处理机制将个体解限制在约束范围内，首先通过离散化方法的标准ICA 框架对解空间进行初步搜寻，其次依托两种种群多样性改进机制进一步提高解的质量。本章将分别介绍基本ICA、算法中个体解的编码表示和修复优化处理、双点自变异算子和跳出局部极值机制。

2.1 基本帝国竞争算法

ICA［15］最早于2007 年被提出，是基于帝国发展与竞争的新型进化算法，种群中的个体称为国家，大种群被分成若干个亚种群，这些亚种群称为帝国，帝国中表现最好的国家称为帝国主义国家，其他国家被称为帝国的附庸殖民地国家，简称殖民地。殖民地在帝国主义国家的殖民影响下，在国家特征上表现为趋同，在算法上表现为空间位置的趋近，该操作为殖民地的同化操作；此外，帝国间通过竞争最弱帝国的最弱殖民地实现不同亚种群间的信息交流。ICA 主要通过以下操作实现：初始化帝国种群操作、殖民地同化操作、交换殖民地与帝国主义国家地位操作、帝国间竞争操作、帝国覆灭操作。目前，ICA 已经成功应用于工厂调度、旅行商、供应链优化设计、能源传输等实际问题的优化中。

2.2 算法中个体解的编码表示和修复优化处理

2.2.1 个体解的编码表示

BICA 采用二进制编码方法，个体解由一条n元编码串X表示，n为该背包问题中物品的数量，编码串上的每个基位取值为1 和0 分别表示该基位所指代物品的状态为已放入和未放入背包。

绝大多数元启发式算法的设计只适合求解连续实数域上的数值优化问题，不能直接处理离散域上的组合优化问题，算法从连续实数域过渡到离散组合域的方法称为离散化方法（Discretization Method，DM）。本文引入两种简单可行的DM 将实数映射为它的等效0-1 变量，这两种方法分别是离散演化算法（Discrete Evolutionary Algorithm，DisEA）［26］、最佳匹配值（Best-Matched Value，BMV）法［21］。

1）DisEA 离散化方法。

设ICA 中个体X的编码为D维实数向量X=(x1，x2，…，xD)（xj∈[-1，1]，j=1，2，…，D），对应组合优化问题的解Y=[y1，y2，…，yD（]yj∈{0，1}）。

定义映射φDisEA：[-1，1] →{0，1}，则Y=φDisEA(X)满足：

2）BMV 离散化方法。

设ICA 中个体X的编码为D维实数向量X=[x1，x2，…，xD]（xj∈[0，1]，j=1，2，…，D），对应组合优化问题的 解Y=[y1，y2，…，yD]（yj∈{0，1}），定义映射φBMV：[0，1] →{0，1}。相较于DisEA 以实数值0 作为从实数域映射到离散域的分界线，BMV 选择实数向量X的算术平均值Avg作为映射操作中的分界线。则Y=φBMV(X)满足：

2.2.2 个体解的修复优化处理

在经典修复法的修复操作和修正操作之上，本文经部分改进提出修复机制（Operation Repair Mechanism，O-RM）与修正机制（Operation Correction Mechanism，O-CM）。

O-RM 如算法2 所示，它的输入端和遍历条件与经典修复操作不同：经典修复操作输入的物品索引列表H1为所有物品按价值密度升序排序所得，且在算法1 的步骤2）中不仅需要判断W和C的大小，还需判断当前物品的状态；而O-RM的输入端的物品索引列表H3为已放入背包内的物品按价值密度升序排序所得，且不需要进一步判断当前物品状态。

O-CM 如算法3 所示，它的输入端、遍历条件、机制触发条件与经典修正操作不同，前两项与O-RM 优势分析同理，此外，经典修正操作无触发机制，而O-CM 以C-W>w'作为触发条件，当列表H2被全部遍历完后算法结束。经典修复法中物品索引列表内元素个数远多于改进后的修正优化机制，O-CM 设置的触发条件能避免当前配置方案下不可能得到进一步优化却仍然迫使修正操作无效运行的情况发生。因此，O-RM 和O-CM 能在一定程度上降低算法修复和优化配置方案的计算复杂度。

算法2 修复机制（O-RM）。

输入X，H3，W；

输出X'。

算法2 中，X是待修复解；H3是已放入背包内的按照价值密度升序排序的物品索引列表；W是当前背包内物品总重量；X'是修复后的可行解。

算法3 修正机制（O-CM）。

输入X，H4，W，w'；

输出X'。

算法3 中，X是待优化可行解；H4是未放入背包内的按照价值密度降序排序的物品索引列表；W是当前背包内物品总重量；w'是背包外物品的最小重量；X'是进一步优化后的可行解。

2.3 种群多样性改进机制

ICA 在进化进程中会因帝国走向崩塌造成种群多样性丧失、亚种群间自主互动行为减少，最终导致算法易陷入局部最优。面对ICA 的不足，BICA 以增强种群多样性为切入点，在殖民地同化操作后，引入了双点自变异算子和跳出局部最优机制为种群提供额外自进化、重组进化的机会，克服算法缺陷从而提高ICA 求解KP 的能力。

2.3.1 双点自变异算子

本文设计了一种新型局部搜索策略：双点自变异策略（Two-Point Automutation Strategy，TPAS），原理如图2 所示。对于每个待变异个体对应的背包配置方案，在已放入背包的物品中随机挑选一件物品1，并在未放入背包的物品中随机挑选一件物品2，将物品1 拿出背包，物品2 放入背包，随后将处理后的方案对应的个体解经O-RM、O-CM 处理，并利用贪婪算子保留子代与父代中的较优个体。KP 的最优解位于约束边界附近，TPAS 基于该特征向下以每个国家当前位置为起始点执行全空间解域的局部搜索。

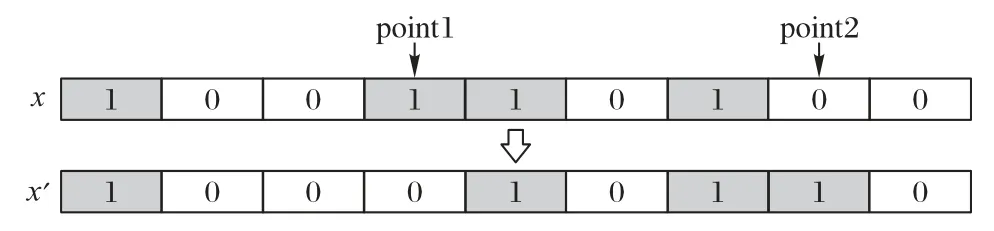
图2 双点自变异策略原理Fig.2 Principal of two-point automutation strategy

ICA 中的个体包括帝国主义国家和殖民地两种角色，本文对两种角色进行不同设计。每个殖民地都有pro_col=0.5 的概率执行TPAS 操作，操作完成即结束。每个帝国主义国家将循环TimesTPAS=50 次TPAS 操作，若当前对应的个体解表现变好或达到最大循环次数，操作结束。

2.3.2 跳出局部最优机制

ICA 在运行过程中种群多样性不断降低，导致算法“早收早敛”；此外，殖民地同化机制和双点自变异操作都引入了贪婪算子，因此算法有更大概率过早陷入局部困境。前期工作发现，当算法陷入局部最优时，保留最优部分解，重新初始化剩余种群能够有效逃逸当前困境。因此，本文设计了一种重新随机初始化种群的跳出局部最优算法（JLOA），当算法只剩下一个帝国或者连续u=20 次最优解都未更新时，保留所有帝国主义国家，剩余殖民地将在约束范围内通过随机初始化的方式产生，并初始化帝国。

综上所述，常规凝血检验项目对异位妊娠大出血输血治疗不良反应监测的应用效果可观，合理应用可以减少输血治疗过程中恶性事件的发生。

文献［27］中也设计了一种跳出局部最优机制，与本文的触发条件类似，不同之处在于触发后的操作。本文通过随机初始化对种群进行处理，相较于前者的重新分配殖民地，更具随机性。JLOA 中的随机性表现为两方面：一方面通过随机初始化的方式初始化所有殖民地；另一方面通过随机分配的方式将所有殖民地分配给帝国主义国家从而初始化帝国，这些随机因子的引入能有效摆脱种群个体在陷入局部最优时小范围解空间的密集群聚现象。JLOA 在算法可能陷入局部最优的节点被触发，通过大范围地初始化种群个体，在平衡算法探索能力和开发能力中扮演了极其重要的角色，保留了种群中最优秀的部分个体，确保前期优化过程的有效性。

2.4 BICA框架

BICA 主要由四部分实现：1）离散化方法，本文对引入DisEA 离散化方法的BICA 命名为BICA-DisEA，对引入BMV离散化方法的BICA 命名为BICA-BMV，两个算法除选用的DM 不同，运行参数和运行机制均完全相同；2）本文改进的修复优化法O-RM 和O-CM 对个体解编码更新后的子代实现检验、修复、优化三流程；3）标准ICA 框架，利用寻优原理中的同化策略、帝国间竞争策略推动算法实现对空间解的勘探和开发；4）本文提出的两种新型改进机制，一方面执行双点自变异策略帮助种群个体实现对自身周围空间的精细搜索，另一方面利用跳出JLOA 给算法在较可能陷入局部最优解的两个节点上提供逃逸通道。以达到算法的最大迭代次数（FEsmax）作为终止运行的唯一条件，BICA 的描述如下。

算法4 二进制帝国竞争算法（BICA）。

输入cou_num，imp_num，n，FEsmax，cimp_num；

输出 Best results。

其中：cou_num是种群中国家的总数量；imp_num是帝国主义国家的最大数量；n是KP 中物品的总数量；cimp_num是当前算法状态下帝国主义国家的数量；FEsmax是算法的最大迭代次数；FEs是算法当前迭代次数。

3 求解HMKP的多级二进制帝国竞争算法

HMKP 作为特殊的组合优化问题，求解过程中算法需要同时处理多约束条件下的多个背包的物品状态。因此算法设计难度较大，但ICA 具有多种群的特点，所以能处理HMKP。本文将ICA 种群结构设计成一种多级种群结构，并将BICA 中的改进机制融入多级二进制帝国竞争算法结构中，提出一种多级二进制帝国竞争算法（MLB-ICA）。

3.1 多级二进制帝国竞争算法结构

定义ICA 中种群的地位为等级，则ICA 拥有帝国和国家两个等级，称为二级结构。帝国为结构中的第一等级，国家为结构中的第二等级。MLB-ICA 在帝国等级之下，增设了王国等级，王国中势力最强的国家不再是帝国主义国家，而是联盟国，王国中除联盟国之外的国家都为联盟国的殖民地，多级结构中帝国为第一等级，王国为第二等级，国家为第三等级。基本ICA 和MLB-ICA 的种群结构如图3 所示。

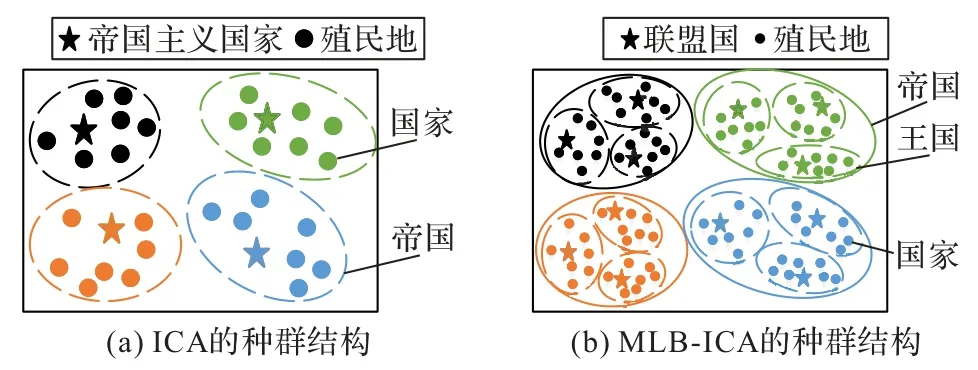
图3 ICA与MLB-ICA的种群结构Fig.3 Population structures of ICA and MLB-ICA

图3（a）展示的MLB-ICA 种群结构对应的是3 个背包的HMKP，帝国中王国的个数对应HMKP 中背包的个数，帝国中每一个王国都对应处理1 个简单KP。种群中帝国的个数为e，当HMKP 中每个背包最优值Optimumi已知时，定义最优值与算法所求得当前背包内物品总价值Vij之差为gapij（i=1，2，…，e；j=1，2，…，m），所有背包的gap值之和定义为GAP，则HMKP 的数学模型可以转换为：

1）交换殖民地与帝国主义国家地位操作的重新设计。多级ICA 结构中，已不存在帝国主义国家，取而代之的是联盟国，当王国中存在某个殖民地表现比当前王国中的联盟国更优时，该殖民地成为新的联盟国，原联盟国下放为王国的殖民地。至此，完成交换殖民地与联盟国地位操作。

2）帝国间竞争最弱帝国中的最弱殖民地操作的重新设计。不同王国中的殖民地个数在多级ICA 结构中保持不变，所以帝国竞争操作难以实行。但对ICA 来说，帝国竞争操作必不可少，没有帝国竞争，帝国间就不能进行有效信息交流。在MLB-ICA 中，设计了最强联盟国的游走操作实现王国间的有效信息交流。处理同一背包的不同帝国的联盟国中，gap值最小的联盟国作为最强联盟国，最强联盟国在处理同一背包的不同帝国的王国中游走，将优质信息在不同帝国间扩散。最强联盟国的游走操作使殖民地有机会向来自其他帝国表现最好的联盟国学习，并且最强联盟国的去处按帝国GAP值的大小通过轮盘赌的方式决定，因此表现最好的联盟国也有机会去到表现较差的帝国中从而改进当前亚种群质量，为殖民地的搜索提供更多指导，进一步提高种群多样性。

3.2 MLB-ICA框架

MLB-ICA 是在经典ICA 结构的基础上，融入BICA 中的双点自变异算子和跳出局部最优策略提出的改进算法。MLB-ICA 以达到最大迭代次数（FEsmax）作为算法终止运行的唯一条件，它的描述如算法5 所示。

算法5 多级二进制帝国竞争算法（MLB-ICA）。

输入cou_num，e，m，FEsmax；

输出 Best results。

其中：cou_num是种群中国家的总数；e是帝国数；m是背包个数，也代表帝国中王国的数量；FEsmax是算法的最大迭代次数；FEs是算法当前迭代次数。

图4 描述了帝国数量设置为8，求解3 个背包组合HMKP条件下MLB-ICA 的算法框架。可以看出，MLB-ICA 依托于BICA 并行求解HMKP，在帝国间信息交互环境中综合考虑所有背包内物品的总价值并评价算法求解得出较优方案，最终输出最优HMKP 方案。从寻优结果来看，HMKP 并非简单地分割出多个0-1KP 并让BICA 分别求解最优解，MLB-ICA追求的是整体最优，这是多组合多约束的KP 求解方案。

图4 MLB-ICA的算法框架Fig.4 Algorithm framework of MLB-ICA

3.3 算法的特性分析

3.3.1 算法的平衡改进机制

导致ICA 全局寻优能力不足，易陷入局部最优的主要原因是帝国间缺少有效的信息交流，种群多样性水平受限。本文提出的两种改进机制以提高种群多样性为目的，TPAS 引导每个殖民地和帝国主义国家（联盟国）通过对编码串上两个基位的翻转对自身周围的解空间不断局部开发；JLOA 克服算法自身不足和贪婪策略的副作用，随机初始化所有的殖民地。在改进算法的逻辑框架中，机制间合理分配任务，同化策略与TPAS 强化了算法的局部寻优能力，JLOA 不断让个体分散于寻优空间的所有角落来为算法提供强劲的全局搜索能力。理论上可以证明改进算法相对标准ICA，开发和勘探能力都得到了较大程度的增强，并且全局探索和局部搜索二者之间能够得到合理的互补和平衡。

3.3.2 算法的时间复杂度分析

计算成本是衡量算法有效性的关键指标，算法的时间复杂度是其中最常用的指标。假定国家总数为a，其中帝国主义国家（联盟国）数为a1，殖民地数为a2，则BICA 和MLB-ICA两个算法在求解物品数量为n、背包个数为m的背包问题时单次迭代的最大时间复杂度分别为O((8a+9)n)、O((8a+9)n)，略大于标准ICA 的O(2an)。

表1 为先进元启发式算法：离散正弦余弦算法（Discrete Sine Cosine Algorithm，DSCA）19］、混合贪婪遗传算法（Hybrid Greedy Genetic Algorithm，HGGA）［18］、基于反向学习的高斯扰动帝王蝶优化（Opposition-based learning Monarch Butterfly Optimization with Gaussian perturbation，OMBO）［28］与BICA 求解0-1KP 时的单次迭代最大时间复杂度对比。后续章节能通过实验发现BICA 寻优效率高，较少次的迭代后就能找到次理想解或理想解。虽然BICA 在单次迭代时间复杂度上不占优势，但是它能以较高效率求解高复杂度问题。值得注意的是，BICA 和MLB-ICA 的最大时间复杂度相同，说明MLBICA 的结构并未在本质上提高算法的计算成本，所以它的结构的设计在理论上很合理。从分析结果看，MLB-ICA 的时间复杂度与背包个数m无明显的直接关系，与KP 中物品的总数量n呈典型的线性关系，所以算法具有很强的适应性和可行性，这对于MLB-ICA 在物流服务场景中的应用至关重要。

表1 不同算法的单次迭代最大时间复杂度对比Tab.1 Comparison of maximum time complexity of different algorithms for a single iteration

4 仿真实验与结果分析

本章通过仿真实验的方法实现以下4 个目标：1）验证BICA 的性能；2）验证本文的改进机制的有效性；3）分析BICA 中部分关键参数选择的合理性和算法的有效性；4）验证MLB-ICA 能够有效求解HMKP 并有较好的性能。引入2个测试集分别进行仿真实验。

测试集1［21］是一个中等规模算例集，根据问题特征中物品重量属性与价值属性之间的关系，算例被分成无相关、弱相关、强相关、完全相关4 类。每类包括5 个算例，算例中物品的数量分别为100、200、300、500、1 000。所以测试集1 共有20 个算例，分别命名为KP01～KP20。

测试集2［29］是一个大规模算例集，根据问题特征中物品的重量属性与价值属性之间的关系，算例被分成无相关、弱相关、强相关3 类。每类包括5 个算例，算例中物品的数量分别为800、1 000、1 200、1 500、2 000。所以测试集2 共有15 个算例，分别命名为KP21～KP35。

算法以达到最大迭代次数（FEsmax）作为终止运行的唯一条件，运行参数如表2 所示。每次实验算法连续独立运行次数Times=50。所有实验均 在 PyCharm 2021.2.3（Professional Edition）集成环境中编写与测试，运行环境为Intel Core i5-10400 CPU @ 2.90 GHz、32 GB 内 存、64 位Windows 10 操作系统，编程语言采用PyThon3.9。

表2 算法运行参数Tab.2 Parameters of algorithms

算法运行参数中，θ值是经典固定值；imp_num(m)、col_num、pro_col、TimeTPAS和u这5 个参数的选取通过前期实验确定，借鉴文献［30］中对算法参数分析的方法，本文将在4.4 节深入分析上述5 个参数对算法的影响。

4.1 BICA在中等规模算例集上的表现与比较

首先，选用中等规模测试集1 测试BICA 的性能，算法最大迭代次数FEsmax=2 000，选取算法运行次数Times=50 的最优解、均值解、算法取得最优解时的当前迭代次数的平均值（简称为迭代次数）、取得理想值的成功率（简称为成功率）建立评价算法性能的指标体系。从测试结果来看，BICADisEA 和BICA-BMV 在测试集1 的20 个算例上都能找到最优理想值，且20 个算例中有19 个算例都能被100%找到最优理想值，仅在KP03 这个算例上，两个算法都未能在每次求解中找到理想值，但成功率非常高，分别为88%和92%。BICADisEA 和BICA-BMV 在20 个算例上的迭代次数分别为18.33和14.41，尤其是完全相关算例和弱相关算例的迭代次数大都接近0，说明两个算法在测试集1 的算例上求解效率较高。

引入采用同样在测试集进行实验的二元学习差分进化（Binary Learning Differential Evolution，BLDE）［31］、二分二元差分进化（Dichotomous Binary Differential Evolution，DBDE）［32］、新型二元差分进化（Novel binary Differential Evolution，Nbin-DE）［21］与BICA-DisEA 和BICA-BMV 进行横向对比，选取均值解作为评价算法性能的指标，测试结果如表3 所示，同等算例中表现最好的结果加粗表示。由于BICA-DisEA 和BICABMV 测试结果的均值解相同，所以在表3 中直接用BICA 代表两个算法。

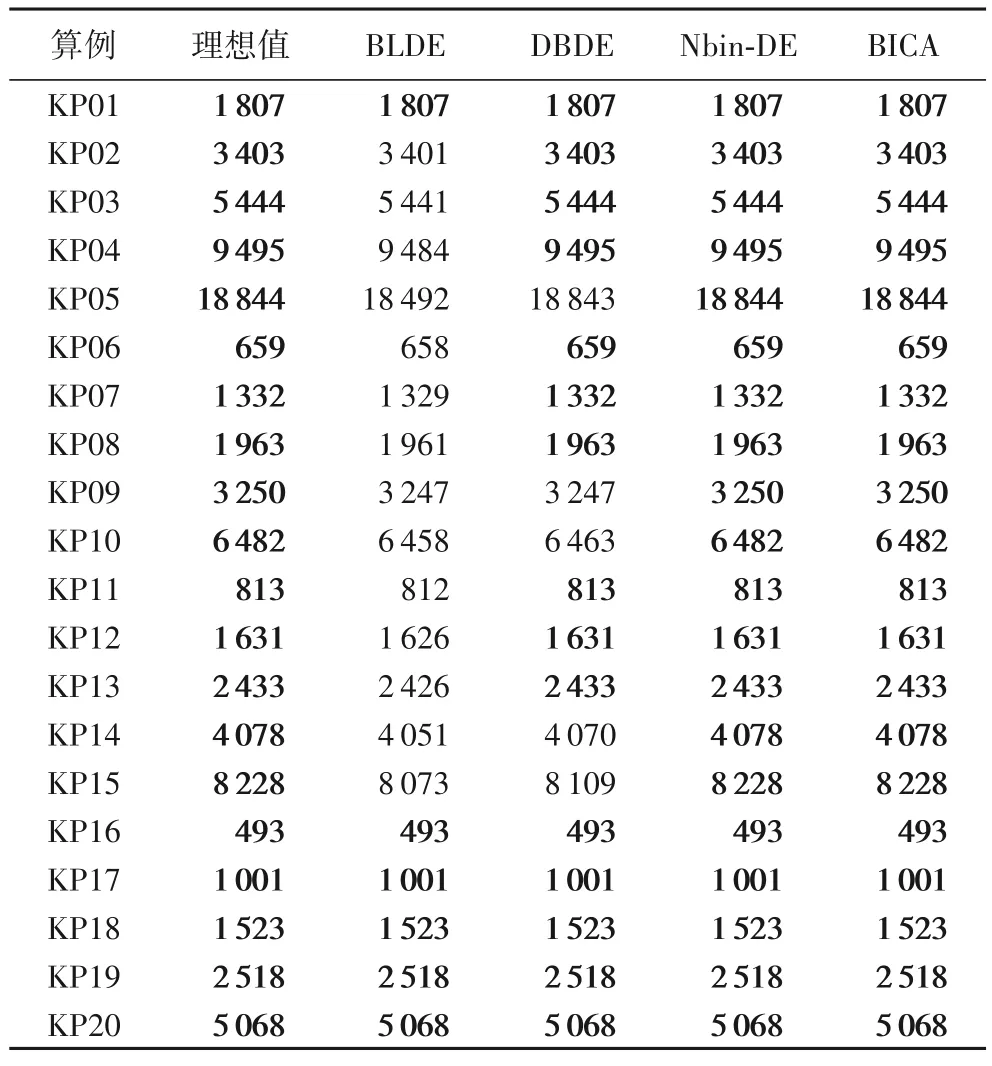
表3 BICA与其他3个元启发式算法在测试集1上的测试结果比较Tab.3 Comparison of test results of BICA and other three meta-heuristic algorithms on test set 1

可以看出，4 个算法中，只有Nbin-DE、BICA-DisEA 和BICA-BMV 能完全获得所有算例的理想值；完全相关算例的求解难度是0-1KP 中最小的。为了解BICA 与其他3 个元启发式算法之间的差异性，应用非参数Wilcoxon 秩和检验在置信水平α=0.05 的条件下进行测试，结果如表4 所示。

表4 基于BICA和3个对比算法表现的非参数Wilcoxon秩和检验测试结果Tab.4 Results of non-parametric Wilcoxon rank sum test based on performance of BICA and three comparison algorithms

可以看出，在求解中等规模测试集1 时，BICA 与BLDE的性能具有显著差异性，与DBDE 间的性能差异不明显。

4.2 BICA在大规模算例集上的表现与比较

为了进一步验证BICA 的性能，在大规模测试集2 上进行测试，算法最大迭代次数FEsmax=5 000，结果如表5 所示。

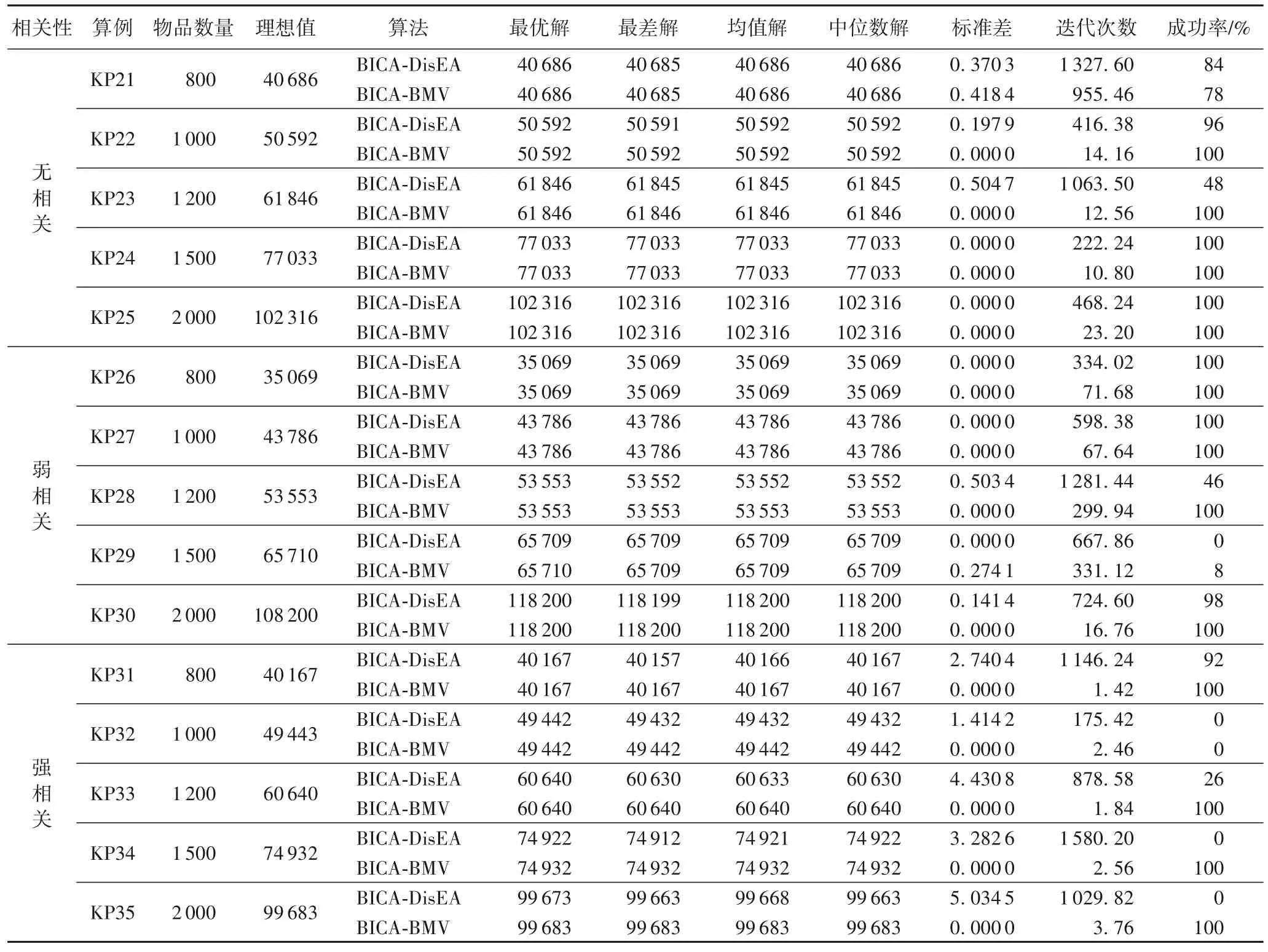
表5 BICA在测试集2上的测试结果Tab.5 Test results of BICA on test set 2

从表5 可以看出，BICA-DisEA 和BICA-BMV 在测试集2的15 个算例上除了KP32 外都能找到理想最优值，但求解KP32 的结果非常接近理想最优值。其中，BICA-DisEA 有4个算例能100%找到理想最优值，BICA-BMV 有12 个算例能100%找到理想最优值。通过最差解、均值解指标能看出，两个算法在未能100%找到理想最优解的算例上的测试结果非常接近理想值。从表5 也能很容易验证BMV 离散化方法对于ICA 求解KP 问题更有效；同时，从迭代次数指标来看，BMV 相较于DisEA，前者应用于ICA 的离散化操作求解KP会更加地高效，因为BICA-BMV 在15 个算例的平均迭代次数为121.02，小于BICA-DisEA 的794.30。

将具有较强求解KP 性能的混沌帝王蝶优化（Chaotic Monarch Butterfly Optimization，CMBO）［33］、OMBO［28］、融合全局势力更新算子的帝王蝶优化（Monarch Butterfly Optimization with Global position updating operator，GMBO）［34］、融合混合贪婪修复算子的噪声方法（Noising Methods with hybrid greedy repair operator，NM）［35］、HGGA［18］与本文的两个BICA 进行横向比较。表6 给出了7 个算法在测试集2 上的测试结果平均排名，平均排名指标参考了最优解、最差解、均值解、标准差4 个评价指标，能较全面地反映算法间的相对性能强弱。

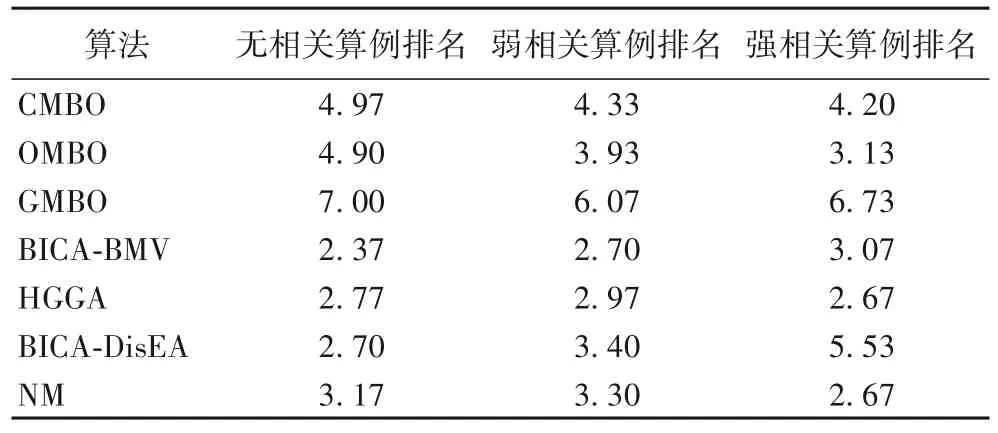
表6 对比算法在大规模算例上的平均排名Tab.6 Average ranking of comparison algorithms on large-scale numerical examples

如表6 所示，在大规模无相关算例的测试结果中，BICABMV、BICA-DisEA、HGGA、NM 这4 个算法表现最好。而从表5 中本文提出的两种算法性能表现可以看出：BICA-BMV的最优解、最差解、均值解都取得了最优；BICA-DisEA 虽然也能找到5 个算例的理想最优解，但测试结果却有欠稳定。

如表5～6 所示，在大规模弱相关算例的测试结果中，除了GMBO，其他算法都有非常好的表现，BICA-BMV 的表现最优，且仅在算例KP29 上未找到最优解。

如表5～6 所示，在大规模强相关算例上，NM 和HGGA 的表现最优，BICA-BMV 仅在算例KP32 未取得理想最优解；相较于BICA-BMV，BICA-DisEA 表现相对较弱，且性能不稳定。

综上所述，7 个算法中BICA-BMV 的性能整体最优，在所有类型问题的测试结果上都具有很高的精度和稳定性。应用非参数Wilcoxon 秩和检验在置信水平α=0.05 的条件下比较BICA-BMV、BICA-DisEA 和5 个先进对比算法之间差异的显著性，显著性p 值如表7 所示。BICA-BMV 与CMBO、GMBO 之间存在显著性差异，与OMBO、HGGA、NM 之间不存在显著性差异；BICA-DisEA 与GMBO 之间存在显著性差异，与其他4 个对比算法之间不存在显著性差异。此外，BICABMV 和BICA-DisEA 之间p 值为0.426，说明两者之间不存在显著性差异。

表7 基于BICA和5个对比算法表现的非参数Wilcoxon秩和检验测试结果Tab.7 Results of non-parametric Wilcoxon rank sum test based on performance of BICA and 5 comparison algorithms

BICA-BMV 和HGGA 是7 个算法中表现最优异的两个算法，两者之间性能差异不明显，表8 展示了两者在都能100%得到理想最优解的9 个算例时的迭代次数，能直接反映算法的寻优效率。可以看出，HGGA 在所有算例的迭代次数都远大于BICA-BMV，说明BICA-BMV 的寻优效率更高，并且在求解大规模强相关算例时该优势更加明显。

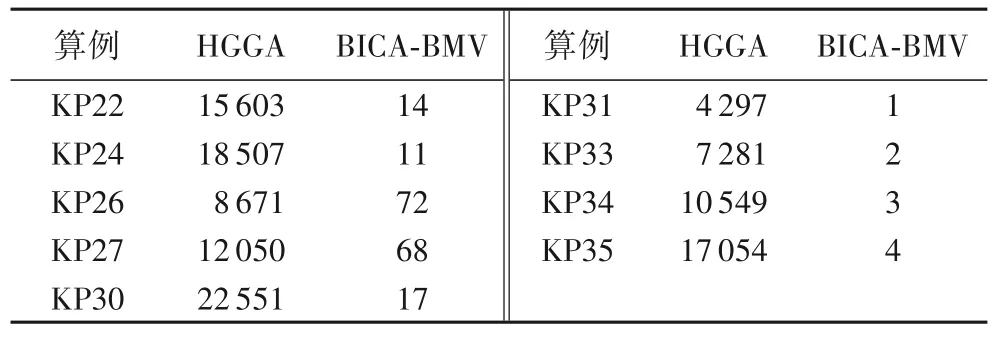
表8 HGGA和BICA-BMV的迭代次数对比Tab.8 Comparison of ierations between HGGA and BICA-BMV

实验结果表明BICA-BMV 的性能优于BICA-DisEA，而BICA-BMV 和BICA-DisEA 之间只有DM 不同，其他参数和机制都保持一致，进一步表明BMV 对于ICA 离散化求解KP 更有效。DisEA 最初提出于粒子群优化（PSO）离散化求解经典折扣背包问题［26］，BMV 最初提出于差分进化（DE）算法离散化求解0-1KP［21］，这两个DM 都适用于本文研究的算法，而ICA 和PSO、DE 有很多本质上的相同之处，都是连续域上的群集智能算法，所以引入DisEA 和BMV 对ICA 来说较合理。对于BICA 中代表个体解的实数向量X，DisEA 以0 作为映射操作的分界线，BMV 以实数向量X的算术平均值Avg作为映射操作中的分界线，前者是固定分界线，后者是动态分界线，这也是BICA-BMV 性能优于BICA-DisEA 的根本原因。对于基于ICA 的改进算法，种群Partitioning 和Clustering 行为具有动态自主交互特性。在实数向量映射为离散向量过程中，BMV 不影响算法的任何行为，但TPAS 需要个体解从离散向量反向映射为连续向量，这个过程BMV 将通过Avg值的动态变化直接引导Partitioning 和Clustering 的交互，从实验结果来看，BMV 给BICA 的寻优带来较多的正反馈。DisEA 和BMV在ICA 上的应用拓宽了它们在算法上的应用，验证了两者的适用性。至少在ICA 上，DisEA 和BMV 对于群智能算法应用于求解离散化问题是有效的手段。

4.3 改进策略的有效性验证

本节将通过消融实验分析各改进策略的有效性。仅以BICA-BMV 作为研究对象并直接命名为BICA；对引入BMV离散化方法的基础ICA 命名为ICA；对仅引入TPAS 改进策略的算法命名为BICA-A；对仅引入JLOA 改进策略的算法命名为BICA-B。表9 给出了它们求解算例KP03、KP21～25 和KP29 的测试结果，测试算例中包括前期实验未能完全取得理想解的算例，以及求解难度较大的无相关算例。

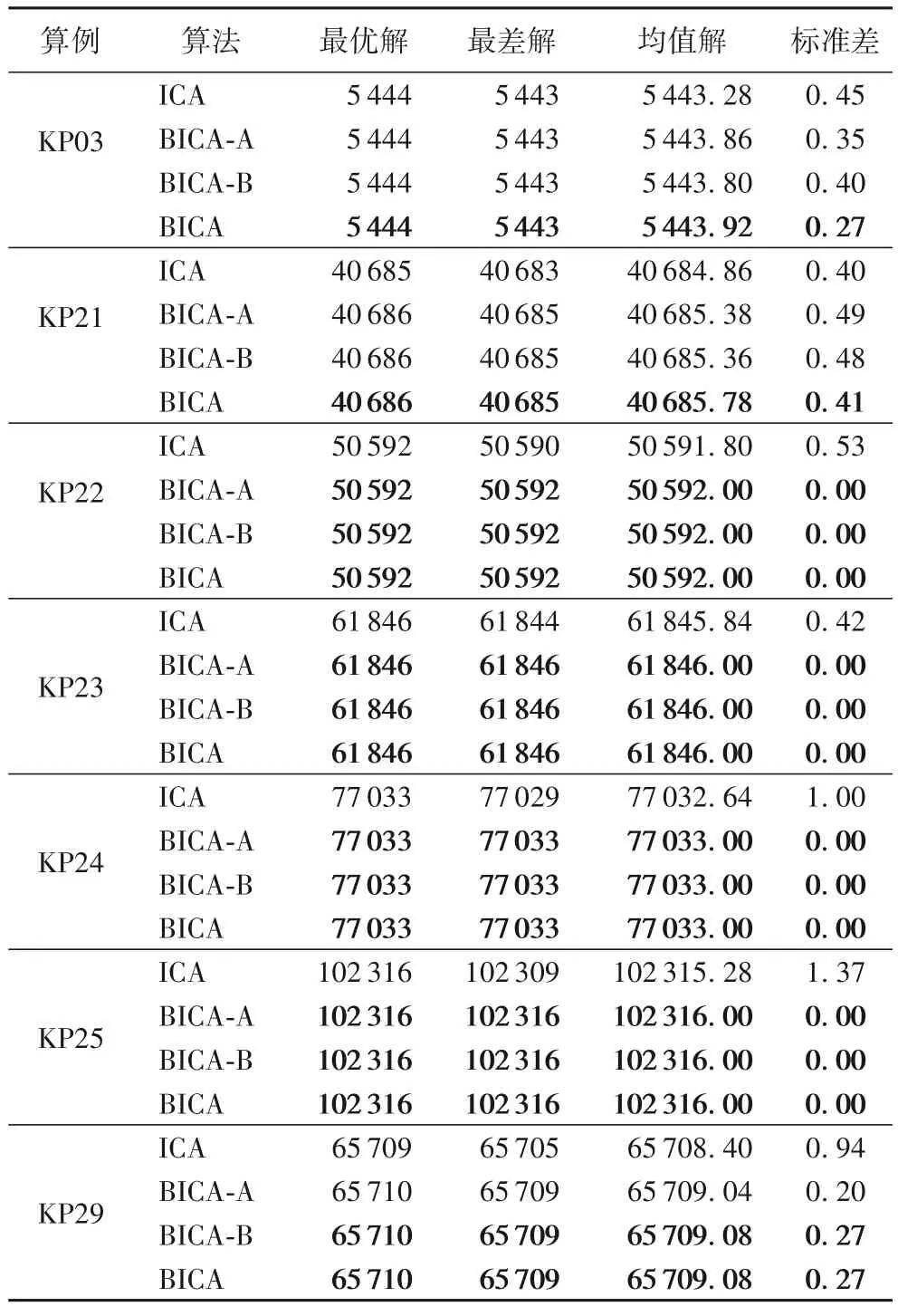
表9 ICA、BICA-A、BICA-B和BICA的测试结果Tab.9 Test results of ICA，BICA-A，BICA-B and BICA

从表9 能够发现，BICA 的测试结果优于其他算法。BICA-A、BICA-B 的测试结果优于ICA，说明TPAS 和JLOA 两个改进策略均能有效提高ICA 的性能。同时，在TPAS 和JLOA 的共同作用下，ICA 的性能得到了进一步提高。图5 展示了4 个算法在相同随机数种子下求解算例KP03 和KP21时收敛曲线。可以看出，4 个算法的收敛能力都较强，但BICA 最优，能在陷入局部最优时更快逃逸出来，当TPAS 未能发挥作用时，JLOA 能给BICA 进一步进化的动力。

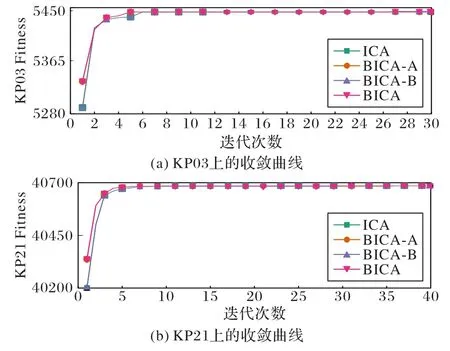
图5 ICA、BICA-A、BICA-B和BICA的收敛曲线Fig.5 Convergence curves of ICA，BICA-A，BICA-B and BICA

4.4 算法关键参数分析

imp_num(m)、col_num、pro_col、TimeTPAS和u对算法演化过程都会产生较大的影响，5 个关键参数可以分为3 组：第1组是国家数量配置参数；第2 组是局部搜索深度参数；第3 组是多级搜索步长参数。下面将分别选取上文中的部分算例对这3 组参数进行具体分析，因ML-BICA 是基于BMV 离散化方法构建的，所以本节只讨论关键参数对BICA-BMV 性能的影响。

4.4.1 国家数量配置参数分析

ICA 是一个基于多种群的算法，Partitioning 和Clustering是它的核心运作原理之一，帝国主义国家（王国）的最大数量在很大程度上代表Partitioning 的水平，而帝国主义国家与殖民地数量的比值能代表Clustering 的水平［27］。当Partitioning和Clustering 之间处于一个相对平衡的状态时，算法的性能会被最大化激发。图6 展示了BICA-BMV 在不同帝国主义国家和殖民地数量配置下求解KP03 和KP21 的成功率。为简化描述，imp_num(m)用a1替代，col_num用a2替代。

可以看出，a1和a2∶a1的增大都能提高算例的成功率；但当a1>8 且a2∶a1>9 时，该趋势不再明显，甚至出现成功率下降的情况。分析结果来看，BICA-BMV 的两个运行参数a1和a2∶a1分别设置为8 和9 比较合理。

4.4.2 局部搜索深度参数分析

TPAS 能帮助算法从基层种群层面进一步精细搜索较优解，pro_col和TimeTPAS决定了局部搜索的深度。帝国主义国家在空间解的搜索中具有关键作用［36］，而TPAS 对帝国主义国家执行操作的设计使它在局部搜索中的关键作用更加明显。本节仅讨论TimeTPAS的选取对BICA-BMV 性能的影响，pro_col选取了一个适中的值，设置为0.5。图7 展示了BICABMV 在不同TimeTPAS取值下KP03、KP21 和KP29 的成功率。

图7 BICA-BMV在KP03、KP21和KP29上的局部搜索深度参数分析Fig.7 Local search depth parameter analysis of BICA-BMV on KP03，KP21 and KP29

从图7 可以看出，随着TimeTPAS增加，算法的求解成功率也在提高。4 组取值中，TimeTPAS=50，75 的综合表现最好。理论情况下，无限地增大TimeTPAS值，算法能够达到最优性能，但是算法计算复杂度会因此线性增加。据实验统计，TimeTPAS=75 的求解时间会比TimeTPAS=50 的求解时间至少增加30 个百分点。综合考虑，TimeTPAS=50 在4 组取值中相对更优，可以认为TimeTPAS值的设置很合理。

4.4.3 多级搜索步长参数

虽然JLOA 有两个触发条件，但算法更容易因为连续最优解未更新的次数达到设定阈值u而触发JLOA。当BICABMV 正常进化时，帝国的数量会随着迭代次数的增加而减小，减小的过程也是算法多极化搜索水平下降的过程，所以本文把参数u值也称为多级搜索步长参数。u越小，算法越容易因为触发JLOA 而重新初始化种群，帝国的数量因此越快恢复为初始值。随着基本ICA 的迭代，帝国数量最终必然归为一。BICA-BMV 迭代过程中帝国数量变化表现为不规则振荡，振荡幅度与u值直接相关。为了更形象展示这个过程，收集BICA-BMV 在u取值为｛20，40，60，80，100｝，求解KP03 时帝国数随迭代次数变化的数据，如图8 所示。可以看出，u值越大，帝国数量变化振荡幅度越大。

图8 不同u值条件下帝国数量的变化Fig.8 Change of empire number under different u values

为了比较u值对算法的影响，选用未能完全取得理想解的算例KP03、KP21、KP29、KP32 进行对比，测试结果如表10所示。从图8 和表10 可以看出，增大u，虽然帝国数量波动范围会变大，但测试结果并没有明显提高，甚至在大部分算例上出现结果变差的情况。考虑到ICA 收敛较快，一个相对较小的u值将引导算法在少量迭代后就触发JLOA，避免过早陷入局部最优。但并不是u越小越好，本文发现u=20 刚好能让算法在帝国数上有变化。从表10 也能发现，u=20时算法表现较优。因此，帝国数量不是最终归一最佳，多极发展对ICA 也是不错的选择，所以将u值设置为20。

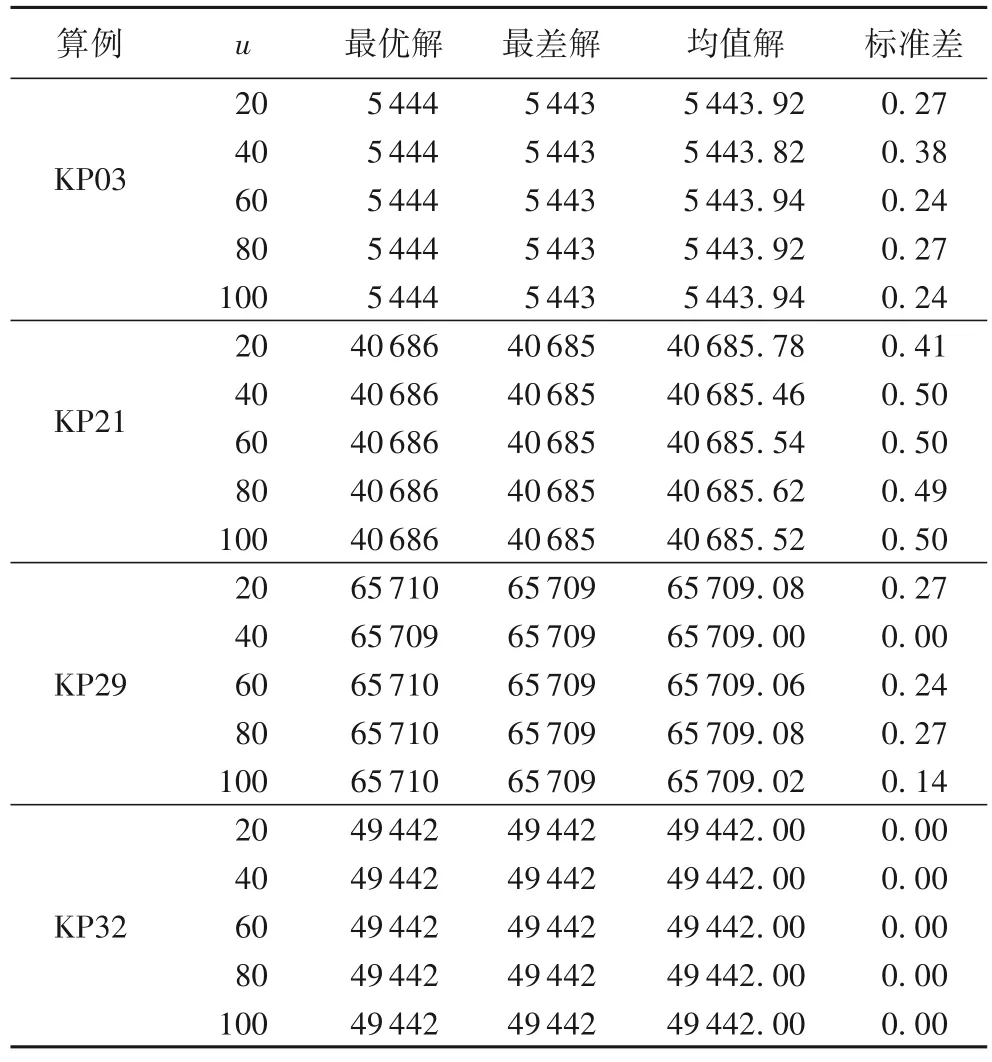
表10 BICA在不同u值条件下的测试结果Tab.10 Test results of BICA-BMV under different u values

4.5 种群进化分析

多极发展是BICA 寻优性能的保证，但这并不代表Partitioning 和Clustering 水平的下降，因为BICA 的种群仍然在迭代进程中不断地实现分区、初始化、重组。基于ICA 寻优原理和改进策略TPAS、JLOA，Partitioning 和Clustering 的交互会更频繁和持续，算法也不断向更优的方向进化。进化是一个全种群变优的过程，可以把种群进化看成是帝国主义国家和殖民地交换地位次数变多的过程。殖民地因为表现比它所在帝国的帝国主义国家更好，会出现交换两者地位的现象，原殖民地成为新的帝国主义国家，原帝国主义国家变为当前帝国的殖民地。本文选取算例KP28 和KP29 进行实验，BICA-BMV 求解KP28 和KP29 时的收敛情况和种群交换地位总次数如图9 所示。表5 的结果说明KP28 和KP29 求解难度较大，且相较于BICA-DisEA，BICA-BMV 在这两个算例上都表现得更好，所以被选取的两个算例具有一定的合理性。

图9 KP28和KP29的收敛情况和种群交换地位次数情况Fig.9 Conditions of convergence and times of population status exchange for KP28 and KP29

基于Partitioning 和Clustering 相关行为的作用，种群进化总体朝变优方向发展，在前期算法最优解提升空间大，所以殖民地与帝国主义国家交换地位的情况发生频繁，算法当前找到的最优解不断更新；到后期算法已经寻找到次理想解，国家种群中的最优个体难以进一步提升势力，因此在势力最强国家所在帝国发生地位交换也较困难，但是此时很可能有部分帝国已经覆灭，重新初始化殖民地会因此初始化新的帝国，交换地位操作在新产生的帝国中又将变得容易，交换地位的总次数进一步变多，这是种群得到进一步进化的表现。这些分析大致符合图9 中曲线特点和变化趋势。

总体来看，BICA 中的改进机制确实改善了标准ICA 在全局寻优能力上的不足，局部寻优能力也得到进一步提升。然而，在贪婪环境中以亚种群-帝国作为勘探载体将面临两个问题：一是帝国数较少；二是帝国内殖民地趋同、聚集特征愈发明显。这使得BICA 面对KP03、KP21、KP29、KP32 这类局部最优解欺骗性大的算例时，空间解的勘探不够全面和细致，会过快收敛到局部最优。在求解测试集1 和2 的算例时，BICA-DisEA 和BICA-BMV 在少量的迭代次数后就能找到最优解，这会增加算法持续陷入局部最优的可能。

4.6 MLB-ICA性能分析

选用测试集1、2 中的算例作为基础算例，分别组合2～6个KP 基础算例，得到测试集3 中的10 个算例，命名为KP36～KP45，物品规模为｛1 800，1 300，1 700，1 100，1 400，800，1 900，2 100，2 200，3 000｝。

采用MLB-ICA 求解HMKP 的性能，算法最大迭代次数FEsmax=1 000，每次实验算法连续独立运行次数Times=50。初始种群中帝国数e=8，帝国中的王国数为m，m根据算例中随机组合KP 的个数而定，每个联盟国附属殖民地的个数为col_num=9，选取测试结果的最优解GAPbest与它对应的gapi、最差解GAPworst与它对应的gapi、均值解、中位数解GAPmedian与它对应的gapi、标准差、平均迭代次数（迭代次数）评价算法性能，测试结果如表11 所示。

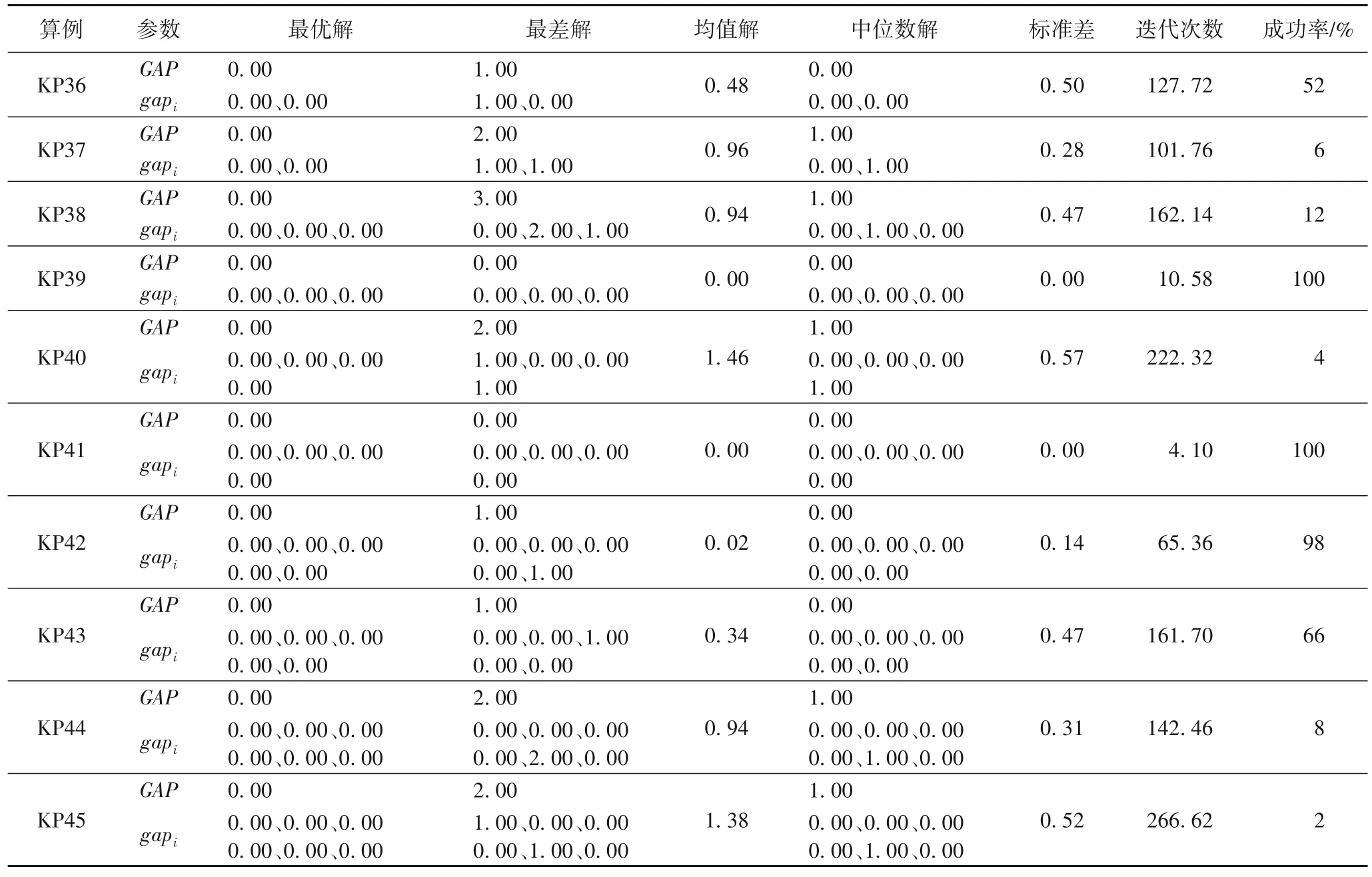
表11 MLB-ICA在测试集3上的测试结果Tab.11 Test results of MLB-ICA on test set 3

表11 中MLB-ICA 的测试结果为理想最优解与当前背包总价值的差值，所以GAP直接反映了算法在当前测试算例的偏离水平，gapi反映了算法在第i个组合算例的偏离水平。组合算例中选取的都是BICA 能够找到理想最优解的算例，可以看出，MLB-ICA 能找到测试集3 中所有算例的理想最优解。组合算例中也并非所有算例都能100%找到理想最优解，这在表11 中也有明显体现。所以，可以认为MLB-ICA 较完整地继承了BICA 的寻优能力和特点，多级ICA 结构起到了桥梁作用。从均值解指标来看，MLB-ICA 的测试结果都非常接近0，说明MLB-ICA 有较高的求解精度。

数学规划求解工具Gurobi 对于求解MIP（Mixed Integer Programming）问题具有通用性，表现出求解速度快、精度高、结果稳定的特点，理论上能有效求解HMKP。通过Python 编译程序调用Gurobi 求解器求解测试集3，并与表11 中的结果进行对比，在验证MLB-ICA 的性能上具有较大的意义。

Gurobi 求解HMKP 表现出非常强的稳定性，这在前期通过较多次数的实验得到了证实，MLB-ICA 和Gurobi 求解器求解测试集3 中算例的均值解和求解时间如表12 所示。

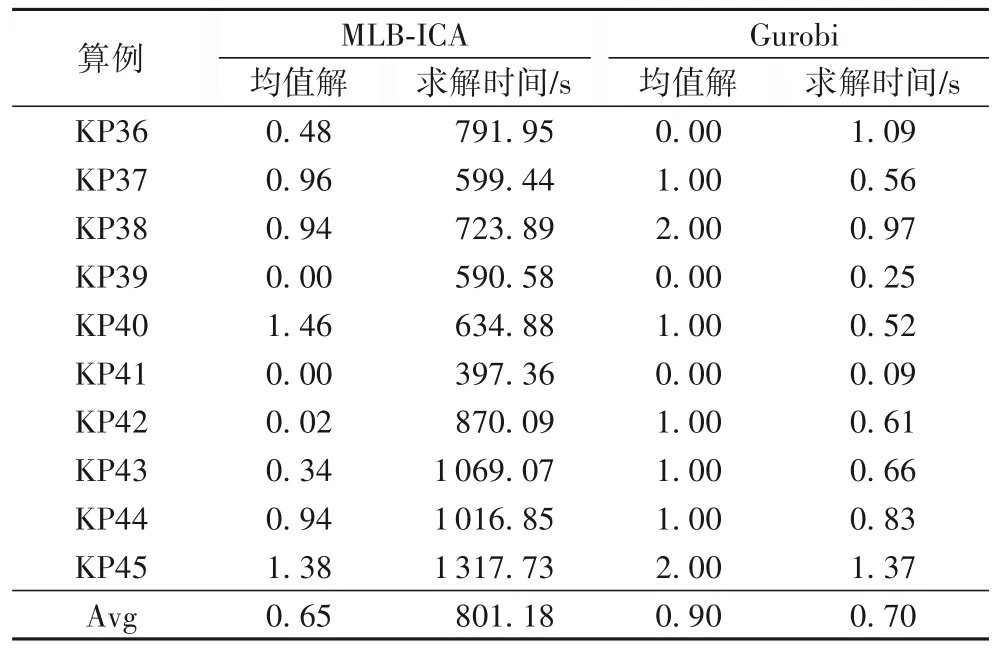
表12 MLB-ICA和Gurobi在测试集3上的均值解和求解时间Tab.12 Mean solutions and solving time of MLB-ICA and Gurobi on test set 3

从表12 可以看出，MLB-ICA 的平均求解精度比Gurobi提高了28%，但求解时间与Gurobi 之间存在较大的差距。MLB-ICA 能在更多的算例上跳出Gurobi 陷入的局部最优，这说明MLB-ICA 也具有较强的全局搜索能力，因此在一定程度上验证MLB-ICA 能有效求解HMKP 并有较好的性能。

5 结语

本文基于传统多背包问题，提出了一种背包问题的新变种—HMKP，针对HMKP 强约束性和高计算复杂度的特性，改进和定制了帝国竞争算法对该问题进行求解。面向标准ICA 的不足和KP 的特征，提出了TPAS 和JLOA 两个策略提高算法求解KP 性能。在O-RM 和O-CM 的监督下，选用高效离散化方法并引入所提改进机制提出了求解0-1KP 的BICA。通过大量实验并与其他元启发式算法进行比较，显示出BICA 全面、高效的寻优能力，实验结果也证明本文所提出的两种改进机制是有效的，BMV 相对于DisEA 能帮助BICA 获得更强的寻优能力。基于BICA 设计了求解HMKP的MLB-ICA，MLB-ICA 依托于BICA 并行求解HMKP，通过10个算例对MLB-ICA 进行了性能测试，并与典型的商业求解器Gurobi 的求解结果进行了详细的对比分析，实验结果表明MLB-ICA 能够有效求解HMKP 并得到优于Gurobi 的测试结果，但在求解时间上，MLB-ICA 占劣势。未来，将结合复杂物流系统的实际服务场景与离线/在线作业需求，对本文所提算法与机制展开面向物流行业的算法修正与应用探讨。