有序规范实数对多相似度K最近邻分类算法

崔昊阳，张 晖，周 雷，杨春明，李 波，赵旭剑

（1.西南科技大学 计算机科学与技术学院，四川 绵阳 621010；2.西南科技大学 数理学院，四川 绵阳 621010）

0 引言

分类是一种有监督的学习方法，目前使用最广泛的分类算法主要有K最邻近（K-Nearest Neighbor，KNN）、支持向量机、决策树、逻辑回归、贝叶斯分类算法等。其中，KNN 算法是一种易于理解和实现的分类算法，具有准确度高、精度高、对异常样本不敏感的优点［1-2］。KNN 的原理是将给定的测试样本与训练样本进行比较，找到与该测试样本最相似的k个训练样本，再根据投票原则确定该测试样本的类别，即该k个训练样本中属于哪个类别的样本数量最多，则判定该测试样本属于此类别［1，3］。因此，有3 个因素对于KNN 算法的性能至关重要，分别为k值的选择、距离或相似度度量方法的选择以及训练数据集［1］。

Abu Alfeilat 等［4］研究了距离测度的选择对KNN 分类性能的影响，可知KNN 分类算法的性能在很大程度上取决于使用的距离或相似度度量方法。目前有多种距离或者相似度度量方法可供选择，如欧氏距离、曼哈顿距离、切比雪夫距离、闵氏距离、余弦相似度、皮尔森相关系数、Jaccard 系数等。然而目前并没有能够适用于所有类型数据集的最佳距离度量，不同的距离或相似度度量方法都有优缺点［4］，方法的原理和侧重点也不同，如余弦相似度是通过两个样本向量之间的夹角的余弦值来衡量，侧重于方向上的相似而非两个样本间距离的远近。因此，在分类时很难对某个数据集选择恰当的距离或相似度度量方法。

针对这一问题，本文考虑通过结合不同的距离或相似度度量方法，实现不同度量方法的互补，从而避免单一度量方法的自身缺点，更加客观、准确地描述样本间的距离或相似度，达到提升分类的准确性目的。为了实现不同距离或相似度度量方法的结合，本文在机器学习算法中引入了有序规范实数对（Ordered Pair of Normalized real numbers，OPN）［5］这一新的数学理论。OPN 是对直觉模糊数（Intuitionistic Fuzzy Number，IFN）和毕达哥拉斯模糊数（Pythagorean Fuzzy Number，PFN）的拓展，通过对OPN、IFN 和PFN 对比发现，OPN 除了可计算IFN 和PFN 无法计算的三角函数、对数等，更重要的是在IFN 和PFN 的定义中，一个实数对中的两个实数之和或平方和的大小都有着严格的限制，而OPN 中却没有这样的限制，所以能通过OPN 更好地将两种不同的距离或相似度度量方法结合起来。因此，本文选择OPN 来结合不同的距离或相似度度量方法。

本文提出了一种将普通数据转化为有序规范实数对（OPN）的方法。通过使用不同的相似度或距离度量方法，将普通数据转化为包含了不同距离或相似度信息的OPN，能实现不同相似度或距离度量方法的结合。由于目前还没有对OPN 进行分类的算法，本文在KNN 算法的基础上进行了改进，提出了基于有序规范实数对的K最近邻分类算法（K-Nearest Neighbor algorithm with Ordered Pairs of Normalized real numbers，OPNs-KNN），对OPN 进行分类，实现了不同距离或相似度度量方法的结合。在多个真实数据集上与多种KNN 的改进算法进行对比，验证了OPNs-KNN 在分类准确率等多个评价指标上具有明显优势，并且在某些数据集上，OPNs-KNN 能够大幅地提升分类的性能。

1 相关工作

KNN 算法是一种广泛使用的机器学习算法，对它的改进一直是研究热点。其中，k值的选择、距离或相似度度量方法的选择以及训练数据集对KNN 算法的性能影响较大。

KNN 算法是一种投票模型，即在选择的k个最近邻中，哪个类别的样本数量最多，就判断测试样本属于该类别。但实际上不同的最近邻对测试样本的分类有不同的贡献，因此可以采用样本距离加权的方法改进KNN 算法。其中代表性的工作有距离加权K近邻规则（distance-WeightedK-Nearest-Neighbor rule，WKNN）［6］以及基于加权表示的K近邻规则（Weighted Representation-basedK-Nearest Neighbor rule，WRKNN）［7］。此外，还可以根据样本中各个属性的重要性的不同，对各属性值进行加权，计算加权后的距离来进行分类，相关的研究有基于属性加权的K最近邻算法［8］等。

目前也有相关研究采用新的相似度计算方法来改进KNN 算法。在实际应用中KNN 算法一般采用欧氏距离分类，然而欧氏距离并不一定适用于所有数据集。目前多种新的相似度或者距离度量方法被提出，相关学者将它们用于改进KNN 算法，并取得了不错的分类效果，如基于熵降噪优化相似性距离的KNN 算法［9］、基于属性值相关距离的KNN 算法［10］、基于Hubness-aware 共享邻居距离的高维数据分类算法［11］等。k值的设定对KNN 算法的分类性能影响较大，但k值的确定比较困难。因此，如何更好地确定k值，也是KNN算法的主要改进方向。相关的研究有动态k值的KNN 分类方法［12］、基于信息熵的自适应k值KNN 算法［13］等。

此外，训练集中的样本对KNN 算法也有着较大的影响，特别是小训练集且训练集样本中存在异常值时。因此，克服异常值的影响对于提升分类的性能以及降低算法对于k值的敏感性都有着非常重要的意义。目前许多相关研究是通过使用K 近邻的局部平均向量来克服异常值，例如基于局部均值的非参数分类器LMKNN（Local Mean-basedK-Nearest Neighbor）［14］、基于局部均值的伪最近邻（Local Mean-based Pseudo Nearest Neighbor，LMPNN）分类算法［15］、基于多局部均值的最近邻分类（Multi-Local Means based Nearest Neighbor classifier，MLMNN）算法［16］以及基于加权局部均值表示的K近邻规则（Weighted Local Mean Representation-basedK-Nearest Neighbor rule，WLMRKNN）。

本文提出了一种基于多相似度的分类算法。通过OPN结合不同的相似度或距离度量方法，实现不同相似度或距离度量方法的互补，从而达到提升算法的分类性能的目的。

2 预备知识

本章介绍了有序规范实数对（OPN）的相关基础知识。

定 义1 将α=(μα，να) 称为一个OPN，其中，0 <μα且να<1。

令α=(0.9，0.8)，因 为0 <0.9 且0.8 <1，所 以α=(0.9，0.8)是一个OPN。但在直觉模糊数（IFN）的定义中，μα+να需要小于等于1，所以α不是一个IFN；同理，在毕达哥拉斯模糊数（PFN）的定义中需要小于等于1，所以α也不是一个PFN。

定 义2 使α=(μα，να)，β=(μβ，νβ)，α和β均为一个OPN，当μα=μβ且να=νβ时，α=β。

定义3α=(μα，να)，β=(μβ，νβ)，α和β均为一个OPN，πα=|μα+να-1|，则α和β之间的距离可以定义为：

与其他模糊数（如IFN 和PFN）相比，OPN 中的两个数的大小限制较少，将普通数据转换为OPN 的方法可以更加方便和多样。因此，本文选择OPN 来结合两种不同的距离或相似度度量。此外，OPN 在数学方面也有一些优势，例如，它可以计算IFN 和PFN 无法计算的三角函数、对数等。

3 有序规范实数对分类算法

3.1 普通数据转化为有序规范实数对

如定义1 所述，一个OPN 中的两个实数间的大小限制较宽松，因此能使用不同方法来生成一个OPN 中的两个实数。

然后通过定义5 所示的方式，将普通数据转换为OPN。

该转化方法是基于Wiswedel 等［17］提出的平行宇宙中学习的范式。相似度或距离度量有很多种，如曼哈顿距离、欧氏距离、切比雪夫距离、闵氏距离、余弦相似度等，可根据数据集的特点选择两种相似度度量方法。该方法涉及的参数为q，不同的q代表计算原始数据之间相似度或距离时所选择的点不同。

可将X2转化为Z2={ (4.123，0.600)，(3.606，0.800) }。

可以看出，例1 得到的两个实数对均不能满足定义1 中OPN 的定义，因此这些实数对还不能被称为OPN。所以本文还提供了一种规范化方法如定义6 所示，将所有实数对全部规范化到（0，1）范围内，从而满足OPN 的定义。

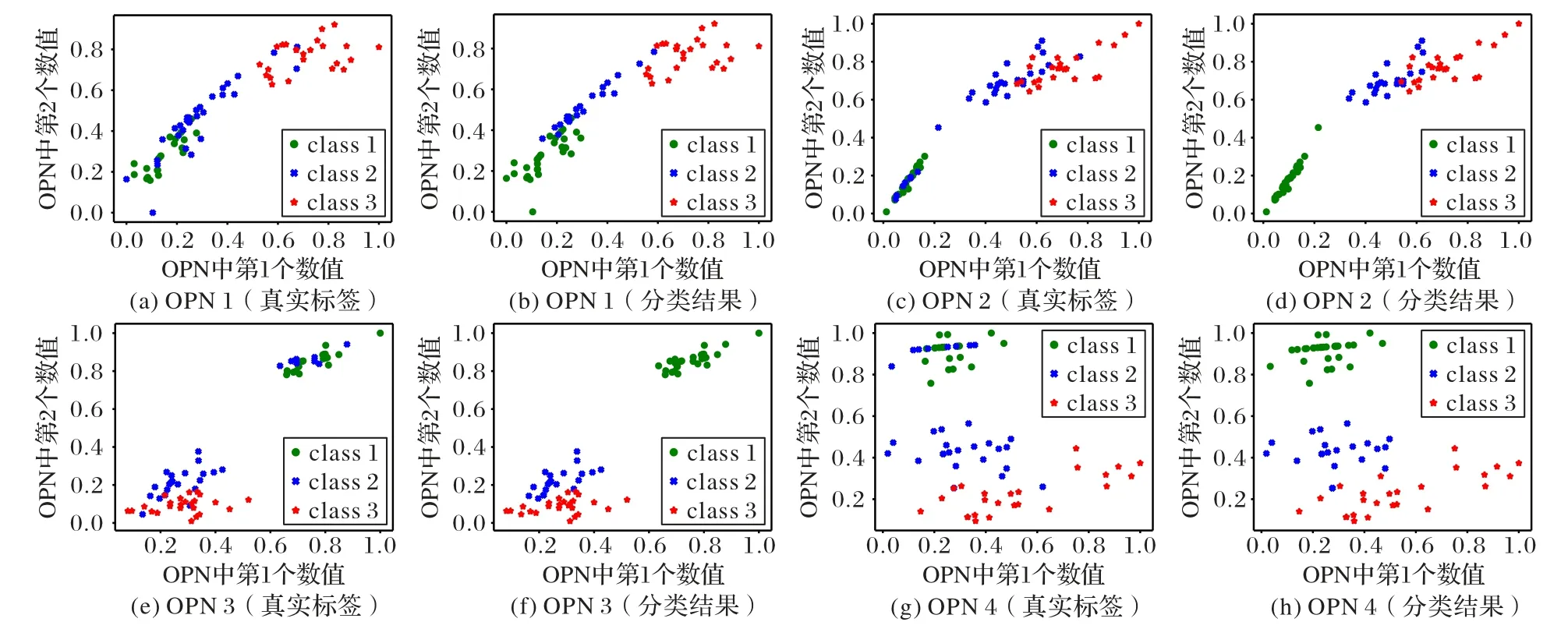
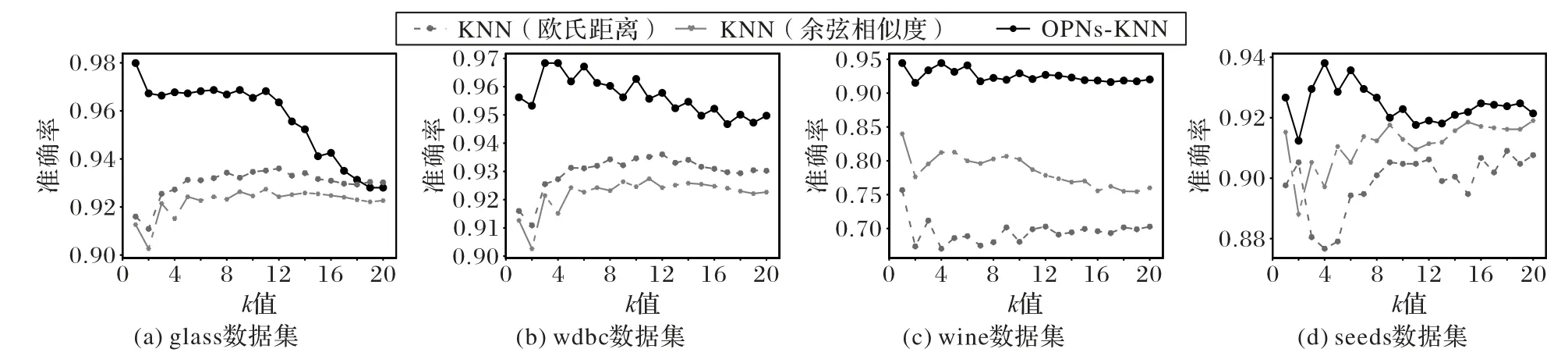
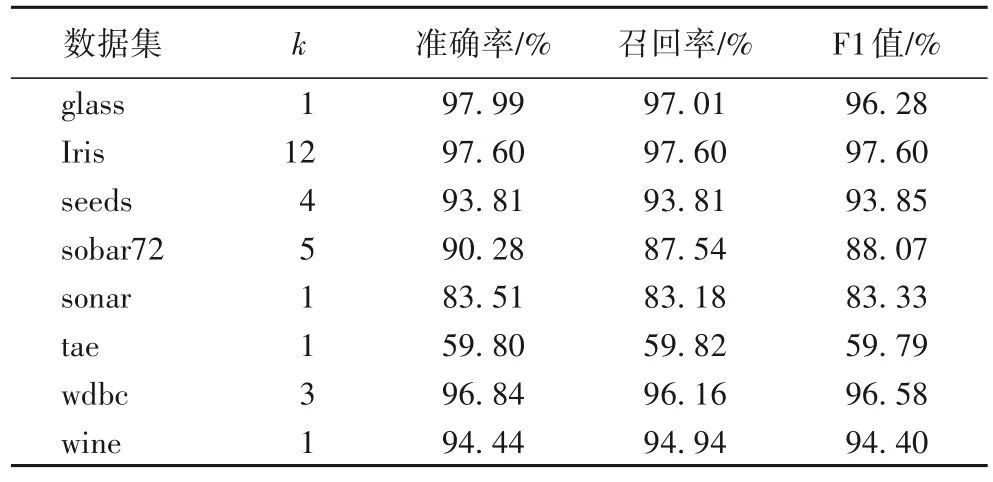
定义6 OPN 数据集Z中具有n个数据，Zj为OPN 数据集Z中的第j个数据(0

图1 以Iris 数据集为例展示了本节的转换方法。Iris 数据集中有3 类数据（class 1～3），每个数据有4 个属性。使用欧氏距离和余弦相似度作为相似度度量，q=10，将每个数据转换为4 个OPN。图1 中的4 个部分分别对应转换得到的4个OPN。每个OPN 中的两个实数分别用作横坐标和纵坐标的值，以展示它们在空间中的位置。

图1 将Iris数据集中的数据转化为OPNFig.1 All data in Iris dataset converting to OPN

从图1 可以看出，在每个子图中，3 个类别的数据都有较好的可区分性，并显示出不同的结构特征。后续的分类算法将综合各个OPN 的差异，得出最终的分类结果。

3.2 有序规范实数对的K最近邻分类算法

KNN 的核心是样本间相似度或者距离的度量。本文将两个OPN 组成的数据间距离定义如下。

定义7Xj和Vi是转化为OPN 后的两个数，且它们均有m个特征，其中：

该距离定义的核心是考虑了在两个相互对应的OPN 之中，它们所包含的相似度信息之间的差异，最后综合各个OPN 上的差异，得出最终的距离。如果相似度信息差异越大，则距离越大；如果相似度信息差异越小，则距离越小。

OPNs-KNN 的具体步骤如算法1 所示。

算法1 OPNs-KNN。

输入 训练集T，测试样本Xj，指定的两种相似度或距离度量方法，q和k值；

输出 测试样本Xj所属类别。

步骤1 利用3.1 节中的方法及指定的相似度或距离度量方法，计算测试样本Xj和训练集中各点与各个坐标轴上与原点距离为q的点的两种距离或相似度，将Xj和训练集中各点全部转化为OPN。

步骤2 利用式（8）计算出测试样本与训练集中各点的距离。

步骤3 选取与测试样本最近的k个训练数据，其中，属于哪个类别的样本最多，则判定该测试样本也属于该类别。

对OPNs-KNN 的复杂度进行分析。由于OPNs-KNN 基于KNN 算法，两者同属于懒惰学习（lazy-learning）算法，新的测试样本需利用式（8）来计算与训练集中各个样本之间的距离，因此算法的时间复杂度与训练样本的数量成正比。设训练集中样本的数量为n，则OPNs-KNN 的时间复杂度可以表示为O(n)。而在空间复杂度上，需存储测试样本与各个训练样本之间的距离，因此空间复杂度可以表示为O(n)。

为了更直观地展示OPNs-KNN 的分类效果，仍以Iris 数据集为例进行可视化展示。将Iris 数据集中50%数据作为训练集，剩余50%数据集用作测试集。如图2 所示，不同形状代表数据的类别，图2（a）、（c）、（e）、（g）为原始数据转化为OPN 后的真实情况（采用数据真实标签绘图）；图2（b）、（d）、（f）、（h）为分类结果（采用OPNs-KNN 的分类结果绘图）。

图2 OPNs-KNN分类结果与数据集真实情况的对比Fig.2 Comparison between classification results of OPNs-KNN and real situation of dataset

由图2 可以看出，OPNs-KNN 给出的分类结果与测试数据的真实标签基本一致，表明OPNs-KNN 在Iris 数据集上有效。有关OPNs-KNN 的性能将在实验部分进一步阐述。

4 实验与结果分析

本文选择准确率、召回率和F1 值对分类效果进行评价［18］。使用scikit-learn 库中的函数来计算上述指标，且召回率、F1 值计算函数中的average 设定为macro。实验采用了UCI 中的多个公开数据集（https：//archive.ics.uci.edu），具体信息如表1 所示。

表1 UCI数据集Tab.1 UCI datasets

为了更准确客观地描述分类算法的性能，实验采用了10 次10 折交叉验证的方法。10 折交叉验证是指将数据集划分为近似相等且互斥的10 个子集，然后每次取出1 个子集作为测试集，剩下9 个子集作为训练集，然后执行分类算法，直到每个子集都轮流作为了一次测试集［19］。10 次10 折交叉验证则是将10 折交叉验证的过程执行10 次。最终取10 次10折交叉验证中各评价指标的平均值作为最终报告的结果。

4.1 OPNs-KNN的参数选择

4.1.1q值的选择

为了研究q的取值对OPNs-KNN 在不同数据集上准确率的影响，本文在各个数据集上进行了实验：将OPNs-KNN 中使用的两种相似度或距离度量固定为欧氏距离和余弦相似度，k的取值固定为该数据集上的最佳k值，只改变q值的大小，q的取值范围为［0.1，20］，每次按0.1 递增，取10 次10 折交叉验证后的结果进行展示。实验结果如图3 所示。

图3 q值对于OPNs-KNN准确率的影响Fig.3 Influence of q value on accuracy of OPNs-KNN

从图3 可知，q值对算法的准确率确有影响，但影响的幅度都不大，并且在部分数据集上，q值的变化对于算法准确率并没有影响。因此，q值的选择并不是影响算法准确率的最主要因素。但综合图3 中算法在各数据集上准确率的变化，在本文所采用的数据集上，推荐将q默认设置为10。

4.1.2 相似度或距离度量的选择

本文尝试了3 种常见的距离度量来与余弦相似度组合进行实验，包括曼哈顿距离、欧氏距离和闵氏距离（其中p值为闵氏距离公式中的参数，不同p值下的闵氏距离度量不同），本文简写为MD、ED 和MKD，实验结果如图4 所示。这3 种距离在与余弦相似度组合后，均有着不错的准确率。因为目前各种距离或相似度的度量方法较多，无法尝试所有距离和相似度度量之间的组合，但从图4 而言，大多数数据集上欧氏距离与余弦相似度搭配均有着不错的准确率，因此本文采用欧氏距离与余弦相似度作为OPNs-KNN 的两种默认相似度或距离度量方法。

图4 不同距离与余弦相似度组合下的OPNs-KNN在各数据集上的准确率Fig.4 Accuracy of OPNs-KNN on each dataset under combinations of different distance and cosine similarity

4.1.3k值的选择

图5 为OPNs-KNN（采用欧氏距离及余弦相似度，q=10）在部分数据集中不同k值下的准确率，并对比了分别采用欧氏距离和余弦相似度的KNN 算法。从图5 可知，OPNs-KNN 与KNN 算法一样容易受到k值的影响，因此k值的选择仍然是OPNs-KNN 的主要问题。同时，OPNs-KNN 相较于采用单一相似度度量方法的KNN 算法，在一些数据集上（如wine 数据集）的准确率提升明显。

图5 k值对OPNs-KNN的准确率影响Fig.5 Influence of k value on accuracy of OPNs-KNN

4.2 OPNs-KNN的性能表现

综合4.1 节，采用欧氏距离及余弦相似度，q取10 为默认参数，表2 为默认参数下OPNs-KNN 在各数据集上的指标。

表2 默认参数下的OPNs-KNN在各数据集上性能表现及对应k值Tab.2 Performance of OPNs-KNN on each dataset under default parameters and corresponding k value

然而默认参数并不是一定为最佳参数，实验中尝试了曼哈顿距离、欧氏距离、闵氏距离（p=3 至10）以及余弦相似度之间的两两组合，q在［0.1，20］范围内按0.1 递增，k在［1，20］范围内按1 递增来寻找最佳参数，各数据集对应的最佳参数如表3 所示。在表3 所设定的最佳参数下，OPNs-KNN在各数据集上的性能表现如表4 所示。

表3 OPNs-KNN具有最佳性能表现的参数设定Tab.3 Parameter setting for OPNs-KNN with best performance

4.3 OPNs-KNN与其他算法对比

将OPNs-KNN 与WKNN、LMPNN、LMKNN、MLMNN、WRKNN 以及WLMRKNN 这6 种KNN 的改进算法进行对比，这些算法的性能由相关文献［7，20］所报道。

表5 中展示了OPNs-KNN 与其他算法的准确率对比，可以看出，OPNs-KNN 在各数据集上的准确率均优于其他算法，分类准确率提高了0.29～15.28 个百分点。

表5 不同算法在各数据集上的分类准确率对比 单位：%Tab.5 Comparison of classification accuracy of different algorithms on each dataset unit：%

同时，将表2 和表5 对比可知，即使在默认参数下，OPNs-KNN 也同样具有较高的分类准确率。在各个数据集上，默认参数下的OPNs-KNN 的准确率仍然超过了最佳参数下的多个算法的准确率。

5 结语

本文将有序规范实数对应用于机器学习算法中，提出了一种利用不同的相似度或距离度量将普通数据转化为包含了不同相似度或距离度量信息的有序规范实数对的方法，并提出了有序规范实数对最近邻分类算法，从而在最近邻分类算法中实现了不同相似度或者距离度量方法的结合和互补。实验结果表明，相较于对比算法，在实验数据集上OPNs-KNN 分类准确率提高了0.29～15.28 个百分点。

目前OPNs-KNN 的准确率仍然主要受k值的影响，这与KNN 算法一致，因此如何降低k值对算法准确率的影响，将是该方法后期进一步改进的方向。同时，除KNN 算法外，在分类、聚类、降维等机器学习任务中，仍有多种算法的性能易受到所选择的相似度或距离度量方法影响（如K-Means、FuzzyC-Means、AGNES 等）；因此本文提出的利用OPN 来结合不同相似度或距离度量的方法还可以进一步推广，在更多算法中通过不同相似度或距离度量的互补，达到提升算法性能的目的。