“将军饮马”模型在初中数学中的迁移运用

⦿ 贵州省毕节市威宁县哈喇河中学 杨徐梦

《义务教育数学课程标准(2022年版)》指出:学生经历数学观察、数学思考、数学表达、概括归纳、迁移应用等学习过程,发展数学核心素养.数学的学习除了基本概念、原理、法则、性质等内容的掌握,更要会用所学知识解决数学问题.这就要培养学生的知识迁移应用能力.“将军饮马”模型在数学中的应用,就是利用“两点之间,线段最短”这一简单的原理解决生活和学习中的许多数学问题.模型的迁移应用可以把复杂的问题简单化,抽象的问题具体化.通过建立联系,形成规律,从而准确地解决数学问题.

1 “将军饮马”情境再现

唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个非常有趣的数学问题.这首诗中将军骑马观望烽火之后从山脚下的A点(如图1)出发,骑马到河边饮马后再到B点宿营,要怎样走才能使所走的总路程最短.

图1

2 “将军饮马”模型

如图2,把宿营地和山脚出发点看作两个点A,B,把河流看作直线a,即在直线a同侧有两个定点A,B,在直线a上找一点C,使AC+BC的值最小.如果点A,B在直线a的异侧,利用公理“两点之间线段最短”就可以解决.下面利用两个模型进行探究学习.

图2

模型一：“异侧两定一动”模型.

已知:定点A,B在定直线l的两侧.

要求:在直线l上找一点P,使PA+PB的值最小.

分析：连接AB,交直线l于点P,点P即为所求点.线段AB的长度即为PA+PB的最小值.

理由：“两点之间线段最短”,可以利用“三角形两边之和大于第三边”来证明.如图3,在直线l上任取一点P′(点P′与点P不重合),连接AP′,BP′.

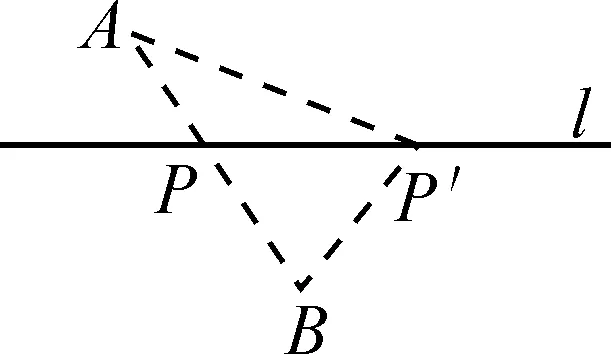
图3

因为在△ABP′中,AP′+BP′>AB,即AP′+BP′>AP+BP,所以当P为直线AB与直线l的交点时,PA+PB的值最小.

模型二：“同侧两定一动”模型.

已知:定点A和定点B在定直线a的同侧.

要求:在直线a上找一点P,使PA+PB的值最小(或△ABP的周长最小).

分析：此问题的关键是要把“同侧两定”转化成“异侧两定”,这样就可以利用模型一来解决.而要实现等距离迁移,就不难想到利用对称来解决.所以可以作点B关于直线a的对称点B′,如图4,连接AB′,交直线a于点P,则点P就是所要找的点.

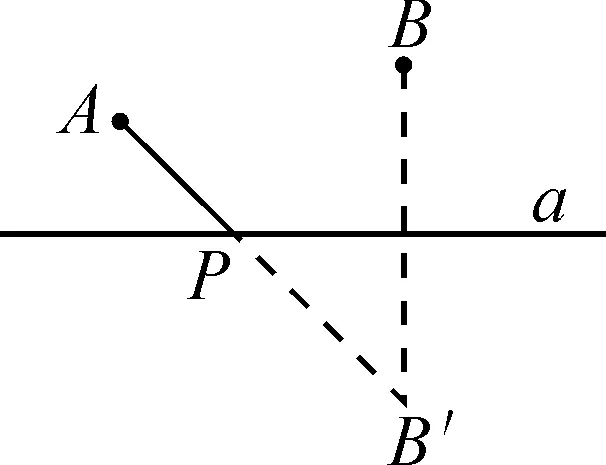
图4

理由：因为PB′=PB,所以可得

PA+PB=PA+PB′=AB′.

3 “将军饮马”模型的迁移应用

3.1 在方案设计题中的迁移应用

例1在河流CD的同侧有两个村庄A,B,A村庄到河流的距离AC=10 km,B村庄到河流的距离BD=30 km,且CD=30 km.现在打算在河边建一个自来水厂,向A和B两个村庄供水,铺设水管的费用为3万元/km,要使铺设水管的费用最省,请你在河流CD上选择水厂的位置M,并求出铺设水管的总费用?

分析：A,B两定点在直线CD的同侧,M是一个动点,所以此题属于“同侧两定一动”模型.

解：如图5所示,作点B关于直线CD的对称点B′,连接AB′,交CD于点M,则AM+BM=AM+B′M=AB′,此时水厂建在点M时,费用最小.

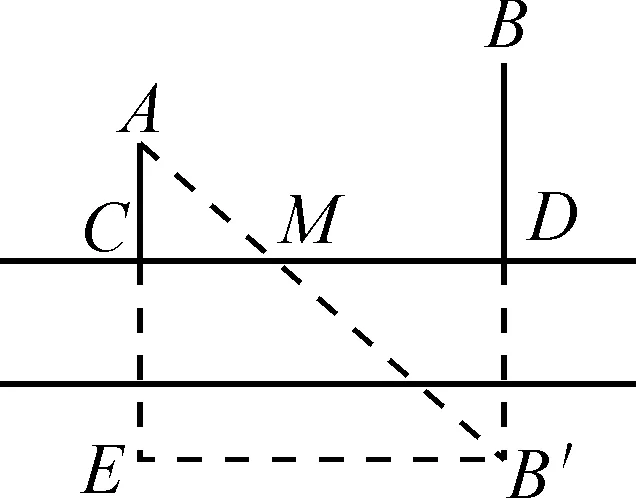
图5

如图5,在Rt△AB′E中,

AE=AC+CE=10+30=40,EB′=30.

所以总费用为50×3=150(万元).

3.2 在代数类题中的迁移应用

例2如图6,P为线段AB上一动点,分别过点A,B作AC⊥AB,EB⊥AB,连接PC,PE,已知AC=4,BE=2,AB=8,设BP=x.

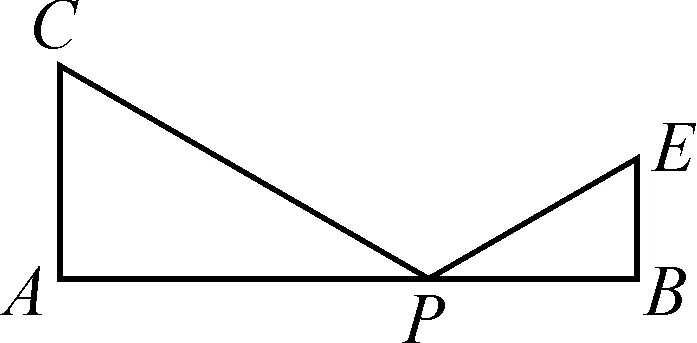
图6

(1)用含x的代数式表示PC+PE的长;

(2)点P满足什么条件时,PC+PE的值最小?

分析：(1)由BP=x,知AP=8-x,则可由勾股定理分别求得PC与PE的长度,进而表示出PC+PE的长.

(2)属于“同侧两定一动”模型,通过作对称,利用两点之间线段最短的原理就可以解决.作点E关于AB的对称点E′,连接CE′,交AB于点P,此时C,P,E三点共线,PC+PE的值最小.

(3)根据(2)中的规律可知,首先画一条线BD=4,分别过B,D作BD的垂线,使得AB=2,DE=1,连接AE,交BD于点C,此时A,C,E三点共线,AC+CE=AE的值最小.

解：(1)由BP=x,得AP=8-x.

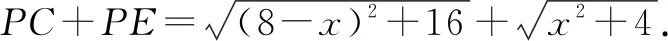
(2)如图7,作E关于AB的对称点E′,连接CE′,交AB于点P,此时C,P,E三点共线,PC+PE的值最小.由对称可知PE′=PE,则PC+PE=PC+PE′=CE′.

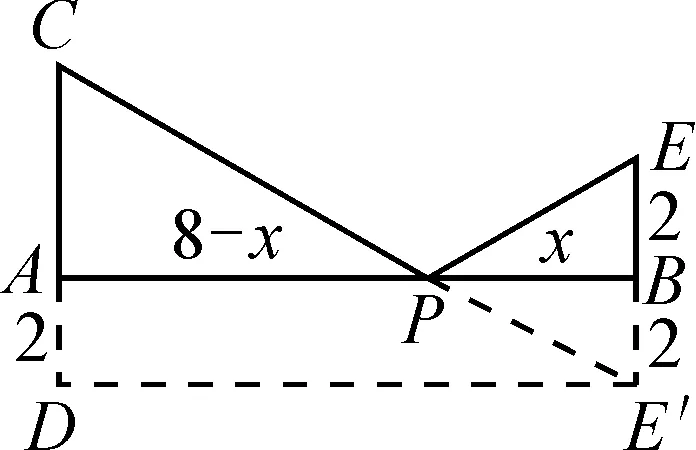
图7

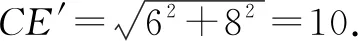
所以PC+PE的最小值是10.

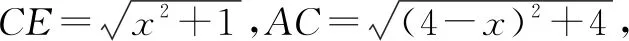
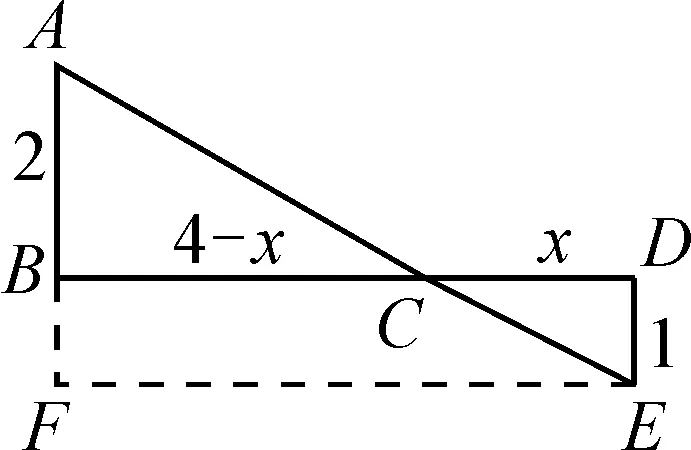
图8

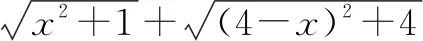
3.3 在图形类题中的迁移应用

例3在△ABC中,AC=BC=6,∠ACB=90°,F是BC边的中点,D是AB边上一动点,求CD+DF的最小值.

分析：两个定点C和F在线段AB的同侧,动点是D,符合“同侧两定一动”模型.通过作一个定点的对称点,转化成“异侧两定一动”模型.

解：如图9,作点C关于直线AB的对称点C′,连接FC′,交AB于点D,则线段FC′的长度就是CD+DF的最小值.

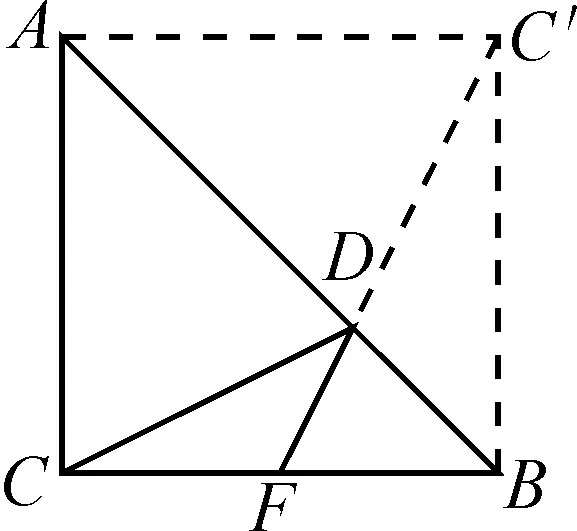
图9

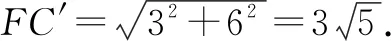
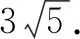
3.4 在函数类题中的迁移应用

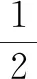
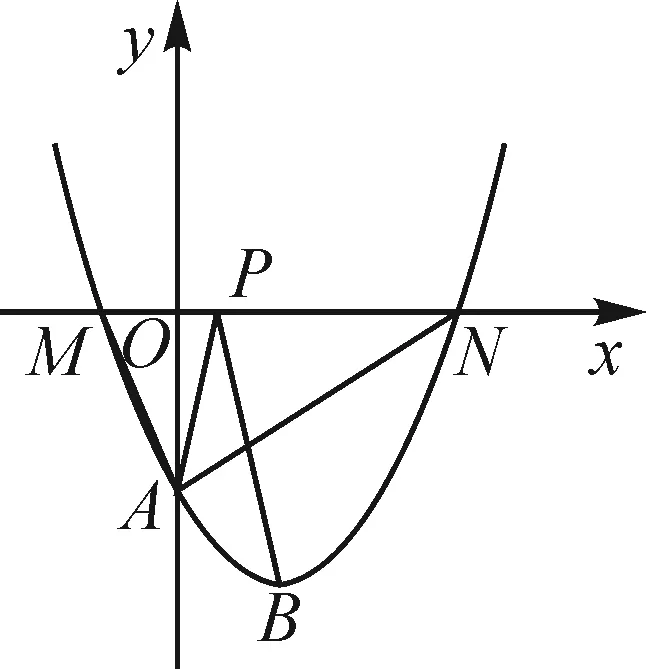
图10

(1)求抛物线的解析式及顶点B的坐标;

(2)判断△AMN的形状,并证明你的结论;

(3)P(m,0)是x轴上的一个动点,当PA+PB的值最小时,求m的值.

分析：(1)(2)略.

(3)从图中可以看出两个定点A和B在x轴的同侧,动点P在x轴上,属于“同侧两定一动”模型.

(2)△AMN是直角三角形.(过程略)

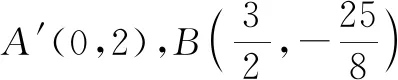
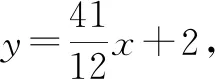
对于“将军饮马”模型类问题,利用轴对称变换,通过化曲为直,把折线路径转化为两点间距离,根据“两点之间,线段最短”求出线段之和或三角形周长最小值,可利用两边之和大于第三边作简单证明.此类问题的解题步骤为:(1)选择模型;(2)作对称;(3)定交点;(4)连路径.