基于“概念图” 的初中数学教学设计与思考*——以“圆的对称性”第1课时为例

⦿江苏省运河中学 袁 健

近日,笔者应邀赴外地参加同课异构课堂教学活动,课题是“圆的对称性”第1课时.拿到课题后,笔者先钻研教材,吃透教材,进而了解学情,研究教法.本人多年来对使用“概念图”组织教学进行了大量的实践探索,本节课也可以使用“概念图”开展教学.

“概念图”是由约瑟夫·D·诺瓦克提出的,是一种知识以及知识之间的关系的网络图形化表征,也是思维可视化的表征.一幅概念图一般由“节点”“链接”和“有关文字标注”组成.“概念图”作为教学设计的工具,有利于教师从一堂课的整体角度入手备课,帮助教师整体把握知识框架和教学思路,增强教师的教学技能.

围绕怎样才能上好这节课进行教学设计,笔者先找到了相关“节点”:圆心角定理及其推论,叠合法,转化思想、数形结合思想、模型思想,三种语言,等等.相关的“标注”:知识准备、方法准备、知识方面、技能方面、数学思想等.用箭头“链接”各“节点”.紧接着,设计了一个本节课的链式概念图[1](如图1).

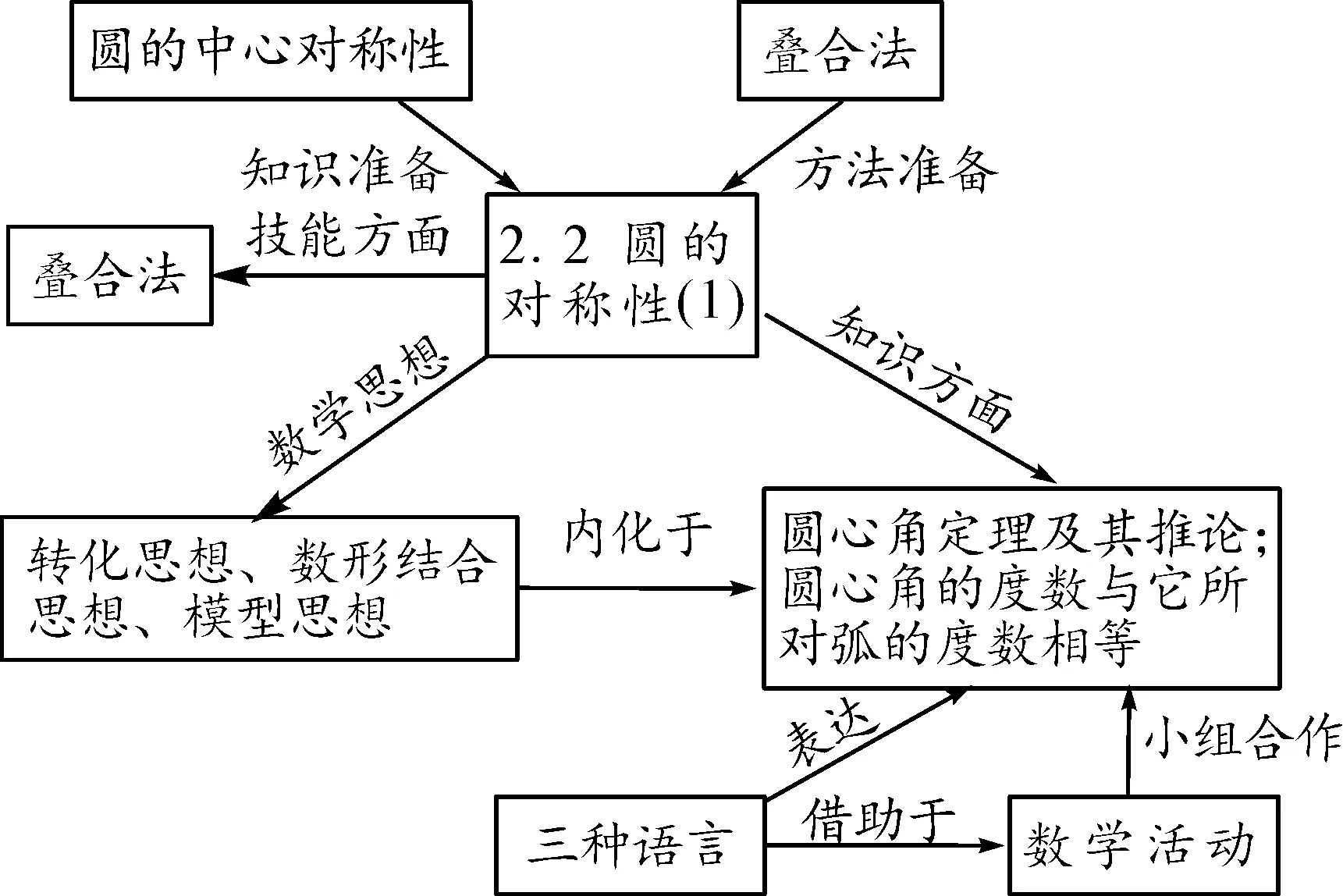
图1

下面从教材研究、“学生”研究、教法研究三方面来阐述笔者借助概念图在开展教学设计中的应用、实践与思考.

1 基于概念图的初中数学教学设计的实践

1.1 教材研究

教师独立开展教学设计,在教学设计中揣摩教材的编写意图,把握教材,对教学内容进行精选和有效整合,合理选择教学策略,编拟教学设计,从而增强自我研究能力.本节课是“圆的对称性”第一节新授课,通过钻研教材,笔者发现中心对称性的知识与叠合的方法是学习本节课的基础.为此,笔者通过概念图中的知识准备与方法准备来设计教学.

环节1：情境创设,提出问题.

(1)摩天轮绕固定轴心旋转180°,它都与初始位置重合吗?摩天轮绕固定轴心旋转任意角度,它都与初始位置重合吗?(2)回顾上节课所学内容,什么是等弧?用什么方法验证两条弧是等弧?

设计意图：通过复习中心对称图形为本节课内容作铺垫.接着通过圆绕圆心的旋转感受它的旋转不变性.在此过程中使用叠合的方法,为本节课的学法指导作了铺垫.

环节2：第一个实践探索——操作、猜想、证明.

(1)在两张透明纸片上,分别作半径相等的⊙O和⊙O′.(2)在⊙O和⊙O′中,分别作相等的圆心角∠AOB,∠A′O′B′,连接AB,A′B′.(3)将两张纸片叠在一起,使⊙O与⊙O′重合(如图2).(4)固定圆心,将其中一个圆旋转某个角度,使得OA与OA′重合.你发现了什么?请与同学们交流.

图2

设计意图：引导学生经历“操作—观察—猜想—说理”的过程,旨在让学生通过自主探究和合作交流探索圆心角定理,感受圆心角、弧、弦之间的关系.引导学生用三种语言掌握,尤其是符号语言.

说明：概念图可以使教师从整体上把握所教内容.但上课时每个环节之间的过渡只有通过精细化的预设,才能更好地启发学生进行下一环节.例如,情境创设之后的引入语——下面我们用圆的中心对称性和叠合法来探究本节课的内容.完成实践探索之后的引入语——借助“蛋筒模型”来感受,在同圆或等圆中,等弧、等弦、相等的圆心角之间可以相互转化.相等的圆心角转化为相等的弧.于是可以得到“在同圆或等圆中,圆心角的度数与它所对的弧的度数相等”.小结反思环节后的引入语——本节课我们用圆的旋转不变性和叠合法来探究了相关性质,下节课我们用轴对称性和叠合法共同探究圆的垂径定理.

过渡性语言起到承上启下的作用,引导学生体会前后知识的联系,对于概念图教学发挥着重要作用.

1.2 “学生”研究

上课不是简单地将教材内容传授给学生,也不是学生配合教师完成任务,而是引导学生进行经验改造,用教材所体现的经验来丰富、发展学生的已有经验.在备课时,笔者会设身处地站在学生的角度来思考怎样学习才能更有效.只有关注学生需要的教学,才有助于发挥学生学习的主体性及增强学生学习的责任感,促进学生自主发展.围绕概念图中知识方面、技能方面、数学思想,笔者精心设计问题导入.

环节3：第一个实践探索环节的变式.

(1)在同圆或等圆中,如果圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?为什么?(2)在同圆或等圆中,如果圆心角所对的弦相等,那么它们所对的弧相等吗?这两个圆心角相等吗?为什么?

设计意图：引导学生经历“操作—观察—猜想—说理”的过程,旨在让学生通过自主探究和合作交流探索圆心角、弧、弦之间的关系.为探索圆心角、弧、弦之间的关系,共提出两个问题,学生在解决第一个问题后,会积累一定的经验与方法,为后面问题的解决提供帮助.在探究过程中,采用“叠合法”说明两条弧相等.通过思考、探索,得出相应的结论并尝试说理,鼓励学生用多种方法和手段进行探究.圆心角定理及其推论生成之后引导学生用三种语言掌握,尤其是符号语言.另外,通过“蛋筒模型”引导学生更形象地理解、记忆和掌握等弧、等弦、等圆心角的相互转化.

这样引导学生自主探索,激发思维,前后衔接紧密.学生也会因为探索目标明确而动力十足.

以问题为切入点的设置符合学生的认知规律,但是如果只是简单地将问题摆出,而没有提示学生后面的问题与第一个问题之间的关系,学生的探索过程难免会割裂整个知识生成过程的完整性.为此,笔者在第一个问题提出后先设置这样的问题:如果将问题(1)中的条件与其中一个结论互换位置,得到的命题正确吗?你能写出推理过程吗?史宁中教授曾经说过:“几何教学要注重原型启发.”为了能让学生更好地使用这三个定理,自如转化“弧、弦、角”三个等量.笔者预设了“蛋筒模型”的图片,引导学生借助生活中的图片来形象理解数学概念及相关转化,观察模型中对应的弧、弦、圆心角,感受在同圆或等圆中,等弧、等弦、等圆心角可以相互转化.

1.3 教法研究

古代教育家孔子将启发式教学概括为“不愤不启,不悱不发”.教师的“启”是为了促进学生的“思”.图1中圆心角定理及其推论的三种语言的表达要借助于数学活动来实现,而数学活动的开展要依赖于小组合作.为了能让学生更好地参与到数学活动中去,备教法时,笔者在设计过程中坚持启发式的教学方法,通过设计问题、解决问题,进行师生互动、生生交流,启发学生感悟知识的生成过程.

上课时,若教师处理不当,往往会出现如下情况:如学生被动的参与多,主动的参与少,即学生的参与只是对教师要求的应对,而不是自主的表现.学生的浅层性参与多,深层性参与少,即学生的参与主要基于教材的知识与答案,而不是基于自己个性化思考的质疑,这种参与没有带来智慧,更谈不上学会深度学习.深度学习是学习者以高阶思维的发展和实际问题的解决为目标,以整合的知识为内容,积极主动地、批判地学习新的知识和思想,并将它们融入到原有的认知结构中,且能将已有的知识迁移到新的情境中的一种学习.

下面结合本节课的授课片断,体现笔者是如何开展学生的深度学习的.

师:下面我们小结一下,在同圆或等圆中,相等的两弧所对的两弦、两圆心角相等吗?(大多数同学跃跃欲试.)

生1:相等.

师:真棒!在同圆或等圆中,相等的两弦所对的圆心角相等吗?两等弦所对的劣弧相等吗?

生2:相等.(大多数学生先用手比划.)

生3:我们还能得到:在同圆或等圆中,两个相等的圆心角所对的两条弧、两条弦相等.

师:太棒了!两等弧、两等弦、两等圆心角在同圆或等圆中是可以相互转化的.为了更好地理解、记忆,你能否用生活中的实物模型来展示它们呢?

学生先是沉默,但眼珠在转动,手指在比划,接着声音就大起来了.

生4:蛋筒.(投影展示)这是我刚画出的两个蛋筒模型,下面部分可以看作两圆心角……

师:你真有数学眼光,想象力很丰富.

为了能让学生更主动地参与,更主动地进行高阶思维、深度思考,即进行自主性、探究性学习及合作性学习,教师应当让学生“有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程”,这也是《义务教育数学课程标准(2022年版)》提出的要求.衡量教学是否采用了先进的教法,关键看是否启发了学生的思维,让学生真正成为学习的主人.

环节4：第二个实践探索环节.

如图3所示,1°的圆心角对应1°的弧,n°的圆心角对应n°的弧,n°的弧对应n°的圆心角.思考:圆心角的度数与它所对的弧的度数相等吗?

图3

设计意图：巩固圆心角定理,在同圆或等圆中,把相等的圆心角转化为相等的弧是圆心角定理的应用和内化.在学习过程中,将刚学过的定理迁移到新的情境中,引导学生自主、探究性地深度学习,积累数学活动经验.

2 基于概念图开展初中数学教学设计的思考

2.1 整体把握教学设计

使用概念图可以帮助教师从整体上把握本节课的知识要点、脉络、框架,对教材进行深度分析;超越教材从“双基”到“四基”,培养学生从“二能”到“四能”;从多个维度把握教材的完整内涵.从文字到符号的理解建构,让学生从知识到素养内化提升,真是“会当凌绝顶,一览众山小”.利用概念图,可以提示教师在上课时使用过渡性语言的时机,进而更自信、更淡定地面对每个学生,同时会让学生感受到教师清晰的上课思路.

2.2 充分考虑学生学情

美国著名心理学家奥苏泊尔指出:“影响学习的唯一重要的因素,就是学习者已经知道了什么.”学生学情的深度分析主要从以下三个方面入手:一是学生的前理解.分析学生的先知、先验,从中定位学生有可能存在的困难之处,进而寻找解决策略.二是学生的内源性.分析学生的兴趣、思维、情感的需要,从中定位学生兴趣的引发处、思维的生长点和情感的共鸣处.三是学生的发展区.分析学生的最近发展区,从中定位学生的发展层次水平,进而选择例题、习题及讲授方式.上节课,学生学习了圆的基本概念,已经运用叠合的操作活动探究了轴对称、中心对称等知识,积累了相关的数学基本活动经验.本节课的设计在此基础上,主要让学生充分动手操作、观察、猜想、验证、说理,发展学生的语言表达能力和思维能力.

2.3 创“模型图”,助力“三会”

设计教学时,笔者创造了“蛋筒”这个模型图.这个模型很形象,它便于学生理解弧、弦、角三者间的相互转化,而且深化了记忆;助推学生形象思维向抽象思维的过渡,让推理过程可视化,加深了知识概念图的生成.创造性地使用模型图,可以降低知识应用的难度.使用模型图,学生“想图形、说推理”,更容易用符号有条理地表达,进而逐步引导学生学会“用数学的思维思考世界,用数学的语言表达世界”.

2.4 设问题串,迁移经验

苏格拉底曾说:“最好的教学方法不是给他们成功的答案,而是向他们提问题.”指向学生关键能力和必备品格的问题一定是有价值的问题,它关联着教材的核心概念.

课后专家们的评课也印证了笔者的一些预设:本节课的教学环节清楚,教师语言过渡自然;教师从实际生活中的场景入手,激发学生的学习兴趣,再通过有目的的操作探究、合作交流、成果展示,启发学生推导、直观体验圆心角定理及其推论;注重数学思考和问题解决,教师设计了一连串的问题,通过不断的提问,问思路、问道理,及时组织学生交流思维过程,提供思考问题的方法,展现解决问题的途径.

因此,分析教材、学情、教法,巧用过渡性语言及设置问题串是使用“概念图”开展教学设计要考虑的要素.创造实物模型辅助学生形象地理解,因而突破了重难点,体现了深度教学设计的理念.尝试使用“概念图”备课,启发学生深入挖掘知识“节点”的内涵及知识“节点”间的联系,引导学生从符号学习走向学科思想和意义系统的建构,培养学生的创新思维和问题解决的能力,提升数学核心素养.