冲击载荷下砂岩的动态力学特性及破坏机制

李 乐，王 成，张红成，张翼飞，陈 嘉

(河南理工大学 能源科学与工程学院，河南 焦作 454003)

煤层上覆地层中厚层坚硬的砂岩通常是采场覆岩中的基本顶，是砌体梁结构力学模型中的骨架，是砌体梁结构重要组成部分[1]，其动态力学特性和破碎特征的研究不仅关乎砌体梁结构的形成，而且影响砌体梁结构的稳定性。在深部岩体开挖过程中，工作面快速推进、高强度开采产生的强扰动应力使砂岩基本顶遭到动载荷冲击[2]。当冲击载荷过大时，产生强动压现象，对巷道而言，导致其变形，出现失稳垮冒，堵塞风路，甚至诱发次生灾害；对采场而言，导致顶板沿煤壁岩切落，严重时，甚至诱发冲击矿压[3]。

为探究冲击载荷作用下岩石的动态力学参数的变化规律，国内外学者借助分离式霍普金森压杆(SHPB)开展了大量的岩石冲击破坏研究。如，金解放等[4]研究了循环冲击作用下岩石的应力-应变曲线的变化规律，发现了岩石的应力-应变曲线可分为：压密阶段、弹性阶段、内部裂纹扩展的加载阶段、第1卸载阶段和第2卸载阶段等5个阶段。宫凤强等[5，6]探究了冲击载荷下岩石的力学参数与应变率的关系，得到了其抗压强度、单位体积吸收能随应变率增加的变化规律。Wasantha等[7]探究了应变率对不同颗粒砂岩力学行为的影响，得到了不同颗粒砂岩的峰值强度均随应变率增大而增加。朱晶晶等[8]开展了花岗岩试样进行单轴循环冲击压缩试验，构建了岩石动态损伤本构模型，可反应岩石强度与应变率的关系。Millon等[9，10]研究了冲击荷载下岩石的力学行为，探究了岩石的能量耗散与应变率的关系。

综上所述，国内外学者已在岩石力学测试方面取得了较为成熟的进展[11-18]。基于此，本研究利用分离式霍普金森压杆装置，开展了冲击载荷下砂岩的动态力学试验，在动态力学的基础上进一步探究了砂岩的动态抗压强度、能量吸收、动态弹性模量在不同载荷下的变化规律，阐述了不同冲击载荷下砂岩的破坏模式及破碎块度分布特征，以期为强动压巷道和采场围岩稳定性控制提供相应的理论依据。

1 冲击载荷下砂岩的动态力学试验

1.1 试样制备

试验所选砂岩试样来自赵固二矿14070钻场埋深800 m处的煤层覆岩，该地段岩层未受到支撑压力的影响，经过测试该地段岩层的单轴抗拉强度为6.03 MPa，单轴抗压强度为66.73 MPa，弹性模量为23.58 GPa，且其具有较好的完整性和均质性。为降低试样厚度引起的惯性效应和端面摩擦效应，参考相关文献[19]，确定试样最佳尺寸，采用∅50 mm×100 mm圆柱体砂岩试样。

1.2 试验设备

试验采用的SHPB装置主要包括：杆件加载系统、信号控制系统、数据采集系统。试验装置压杆的材料为40CrMoV合金钢，其直径为50 mm，纵波波速为5172 m/s，弹性模量为210 GPa，泊松比为0.3，屈服强度≥1.0 GPa，入射杆和透射杆长度均为3000 mm，冲击杆长度为400 mm，试验利用氮气加压给冲击杆加速，并使用激光测速仪测量冲击杆的撞击速度。

1.3 试验原理

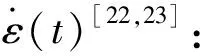
式中，A为SHPB压杆的横截面积，m2；E为SHPB压杆的弹性模量，MPa；C为SHPB压杆的纵波波速，m/s；As和ls分别为岩样的横截面积和长度；εI(t)、εR(t)、εT(t)分别为SHPB压杆的入射应变、反射应变和透射应变。

1.4 试验方案

为了探究动力扰动对砂岩的动态力学特性及破碎机制的影响，开展了冲击载荷下砂岩的动态力学试验，其思路为：为了模拟砂岩所受不同程度的动力扰动，利用分离式霍普金森压杆冲击砂岩试样，参考河南理工大学霍普金森压杆试验经验总结[24]，试验冲击气压采用0.3、0.4 MPa分别在冲击杆长度为1.5、1.7 m时进行冲击，砂岩试样受到10、11、12、13 m/s四种冲击速度冲击。在试验过程中，冲击杆的速度无法精确控制，导致冲击速度数值出现误差，在本研究中忽略冲击速度数值误差产生的影响。

2 砂岩SHPB试验结果与分析

2.1 平衡验证

通过调节SHPB装置的氮气气压，改变冲击杆的冲击速度，以达到动力扰动的效果。为了保证冲击载荷下砂岩的动态力学试验结果的可靠性，需在冲击试验开始前，进行SHPB冲击平衡验证，得到一维应力波的平衡验证曲线，如图1所示。从图1的试验波形可以看出：入射波与反射波之和与透射波的波形曲线基本吻合，表明分离式霍普金森压杆冲击岩样时达到应力平衡，可以认为冲击载荷下砂岩的动态力学试验结果可靠。

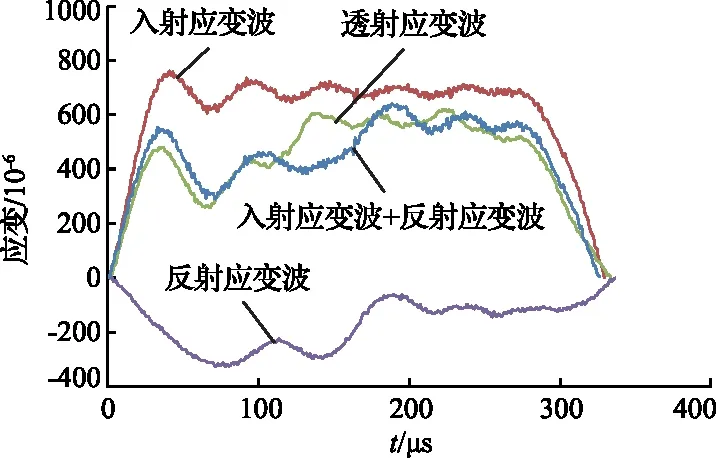
图1 一维应力波的平衡验证曲线

2.2 应力-应变曲线

为了模拟动力扰动对砂岩变形特征的影响，冲击载荷下砂岩的动态力学试验以不同的冲击气压对砂岩进行加载试验，表1给出了典型砂岩试样冲击试验物理力学参数。为了反映出砂岩在冲击载荷作用下的变形特征，典型砂岩试样的应力-应变曲线如图2所示。

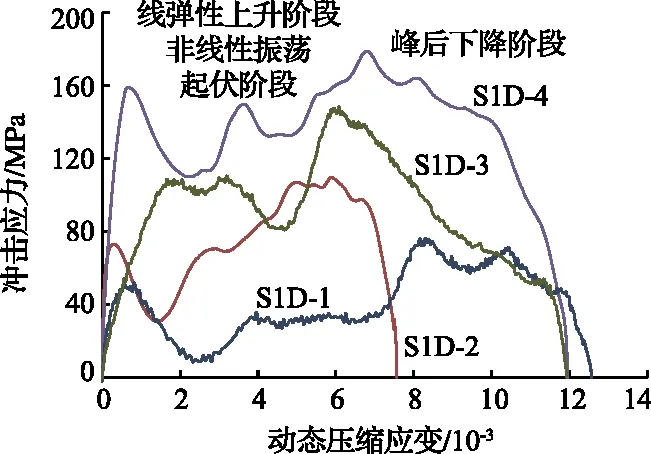
图2 典型砂岩试样的应力-应变曲线

由图2可知：砂岩的应力-应变曲线整体趋势一致，峰值强度前都呈先增大后降低振荡起伏的趋势，到达峰值强度后，都呈降低的趋势。在应力-应变曲线加载的初始阶段，此时的应力-应变曲线几乎吻合，都近似呈直线上升趋势，说明在冲击载荷的作用下，砂岩内部的微裂隙未经历压密阶段，直接进入线弹性变形阶段，这一阶段砂岩具有较好的线弹性变形特性，体现为应力-应变曲线呈近直线上升趋势。

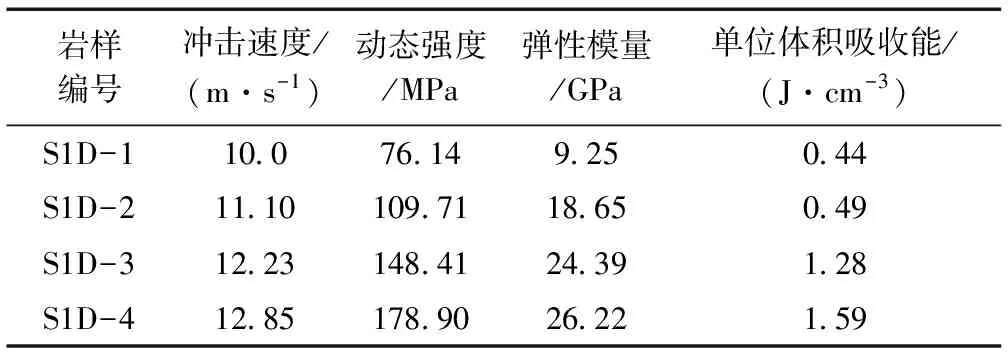
表1 典型砂岩试样冲击试验物理力学参数

在应力-应变曲线振荡起伏阶段，其斜率发生变化，呈非线性关系。由于加载应力逐渐增大，试样进入屈服阶段，砂岩内部的微裂隙逐渐增加。砂岩内部的微裂隙在应力波作用下快速扩展，驱使砂岩发生塑性变形，但此时砂岩微裂隙尚未大量贯通，并未产生宏观破坏。此外，由于在试验过程中，分离式霍普金森压杆撞击产生震颤，导致系统监测的入射应力波、反射应力波和透射应力波产生振荡起伏，体现为应力-应变曲线呈振荡起伏的趋势。

在应力-应变曲线峰后下降阶段，应力-应变曲线的斜率逐渐减小。这是因为砂岩内部的微裂隙产生宏观破裂，导致损伤加剧，降低了砂岩试样的承载能力。当应力完全卸载后，砂岩的应力-应变曲线呈归零现象。

2.3 动态抗压强度与冲击速度的关系

砂岩的动态抗压强度可直接反应出砂岩抵抗外部冲击荷载的能力，典型砂岩试样的动态抗压强度与冲击速度的关系如图3所示。

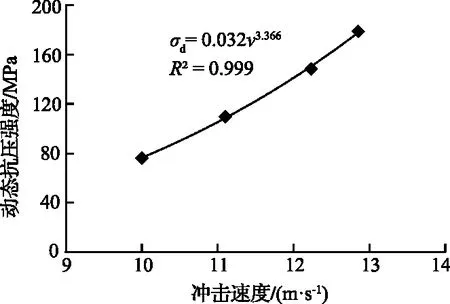
图3 典型砂岩试样的动态抗压强度与冲击速度的关系

由图3可知，砂岩的动态抗压强度具有冲击速度效应，砂岩的动态抗压强度随着冲击速度增大呈幂函数的形式上升，说明砂岩的动态抗压强度随着冲击速度增大而增大。这是由于在冲击载荷的作用下，砂岩试样内部微裂隙的产生和贯通导致了砂岩试样的破坏。但是试验中砂岩岩样受到动载冲击的时间极短，能量积累不足，砂岩岩样只能以提高应力的方式来平衡外部冲击载荷。

2.4 能量吸收与冲击速度的关系

通过岩石单位体积吸收能可以评价岩石破坏过程中的动态特征，典型砂岩试样的单位体积吸收能与冲击速度的关系如图4所示。

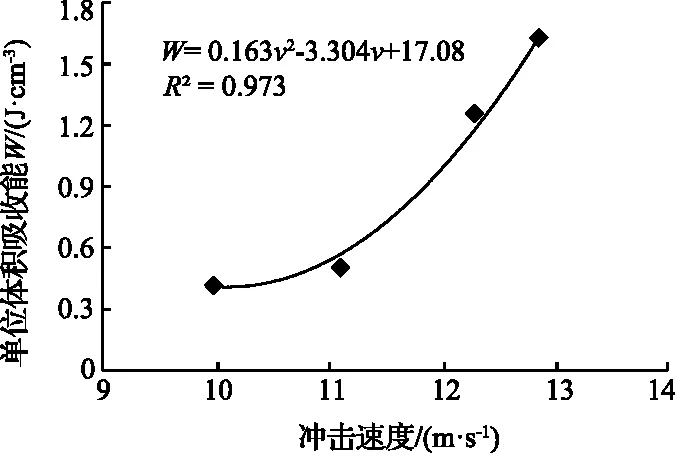
图4 典型砂岩试样的单位体积吸收能与冲击速度的关系

由图4可知，砂岩的单位体积吸收能具有冲击速度效应，砂岩的单位体积吸收能随着冲击速度增大呈二次函数的形式上升，说明砂岩的单位体积吸收能随着冲击速度增大而增大。这是由于砂岩试样内部的微裂隙的产生、发展和贯通都需要能量的参与，并且微裂隙产生所要吸收的能量比其发展、贯通需要的能量高。当砂岩试样所受冲击速度较小时，产生的能量较低，只能激活所需能量小的微裂隙，此时砂岩试样所需吸收能较小；反之，当砂岩试样所受冲击速度较大时，产生的能量变大，在微裂隙扩展贯通之前，需要将大量的能量用于激活所需能量大的微裂隙，此时砂岩试样所需吸收能增大。

2.5 动态弹性模量与冲击速度的关系

通过对砂岩的动态弹性模量变化规律进行分析，可得出砂岩的变形特性，并进一步分析出冲击速度对砂岩变形特性的影响。砂岩的动态压缩曲线不同于静载压缩曲线，因此无法直接确定砂岩的动态弹性模量。通过分析砂岩的应力应变曲线，可发现峰值强度前的应力应变曲线几乎均呈非线性上凸趋势，说明该阶段砂岩处于塑性变形阶段。因此，砂岩的动态弹性模量通过砂岩的应力应变曲线峰值应力点与原点连线的斜率来表示，进而表示出砂岩的压缩变形特性，典型砂岩试样的动态弹性模量与冲击速度的关系如图5所示。

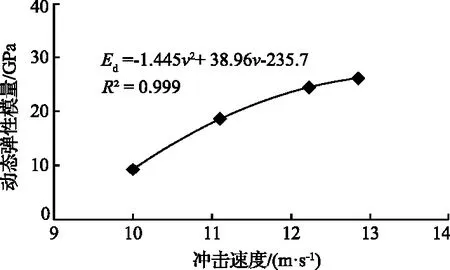
图5 典型砂岩试样的动态弹性模量与冲击速度的关系

由图5可知，砂岩的动态弹性模量随着冲击速度增大呈二次函数的形式上升，说明砂岩的动态弹性模量随着冲击速度增大而增大。这是因为冲击速度越大，导致砂岩试样受到的冲击荷载增大，组成岩样的微元体伴随的能量也就越大。但是试验中砂岩试样受到的动载冲击时间极短，导致岩样内部的能量无法完全耗散，进而影响岩样的变形程度。

3 冲击载荷下砂岩的破坏机制

3.1 冲击载荷作用下砂岩的破坏模式

砂岩的破坏过程亦是砂岩内部微裂隙间相互作用的过程，其破坏模式可有效反映出砂岩所经历的荷载历程，因此分析砂岩的破坏模式有着重要的意义。观察冲击动载下砂岩的破坏形态，并给出典型砂岩试样的破坏形态，如图6所示。

图6 典型砂岩试样的破坏形态

由图6可知，砂岩的破坏程度随着冲击速度的增大而增大。冲击速度10.0 m/s时，岩样破碎程度不明显，仅边缘崩落，呈片状和长圆柱状，其破坏模式以拉伸破坏为主；冲击速度11.1 m/s时，岩样破碎以短圆柱状和长圆柱状，伴有少量碎块，其破坏模式以拉伸破坏为主；冲击速度12.2 m/s时，破坏程度加剧，呈现以两个较长半圆柱状为主，配少量片状、锥状、长条状和碎屑等破坏形态，表征砂岩岩样以拉破坏为主剪破坏为辅的破坏模式；冲击速度12.9 m/s时，岩样完全破坏，冲击速度的增大，加快了砂岩内部微裂隙的产生和贯通，砂岩的碎块数量明显增加，砂岩的破碎程度愈发明显，导致砂岩呈现短长条状、短半柱状、三棱锥状、碎屑状和不规则块状等，表征砂岩岩样在冲击载荷作用下产生拉-剪耦合型破坏。

3.2 冲击载荷作用下砂岩破坏的块度

破坏岩块块度可有效反应其破碎状况，也可以反映出破坏岩块块度随冲击速度变化规律。冲击载荷下砂岩的破坏模式随冲击速度增大由拉伸破坏向拉-剪耦合型破坏转化，为进一步分析冲击速度对砂岩破坏特征的影响，试验后对冲击载荷下破坏岩块块度进行统计分析。当破坏岩块块度小时，则统计意义不大，试验参考王春等[25]所用的破坏岩块尺寸量取方法，选取的破坏岩块以长度大于35 mm为准。破坏岩块数量、岩块最大长度和冲击速度的关系如图7所示。

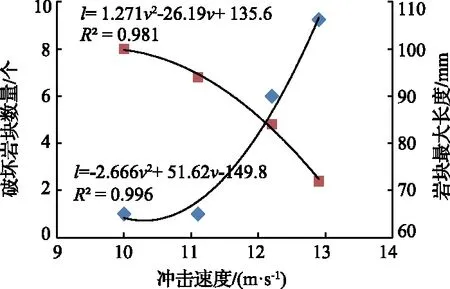
图7 破坏岩块数量、岩块最大长度和冲击速度的关系

由图7可知：块度尺寸大于35 mm的岩块数量随着冲击速度的增大呈二次函数的关系上升，而破碎岩块最大长度则随着冲击速度的增大呈二次函数的关系下降，说明冲击载荷作用下砂岩破坏的块度随着冲击速度增大而减小。当冲击速度较小时，冲击载荷较小，少量的能量只能使岩样出现细微的破碎；随着冲击速度增大时，冲击载荷增大，岩样的破碎程度加剧；当冲击速度较大时，岩样多次拉-剪破坏，形成宏观破裂面，导致其损伤加剧，增大了砂岩试样的破碎程度，最终导致破坏后岩块的块度减小。

3.3 冲击载荷作用下砂岩块度的分形特征

岩石的分形特征可以反映岩石的破裂机制，为了探究不同冲击速率下砂岩的破裂机制，试验采用粒径分级的方法深度分析试验现象，对破碎岩块的最长边进行统计测量，称量各粒径下累计的碎块质量，并绘制二者关系图。不同冲击速度下典型砂岩的破碎块度分布规律如图8所示，典型砂岩的ln[M(R)/MT]-lnR曲线如图9所示。并基于式(2)和式(3)对分形维数进行计算[26]。

D=3-b

(3)

式中，b为ln[M(R)/MT]-lnR双对数坐标系中拟合函数的斜率；M(R)为粒径小于R时累计的碎块质量；MT为砂岩岩样质量；D为砂岩碎块的分形维数。

图8 不同冲击速度下典型砂岩试样的破碎块度分布规律

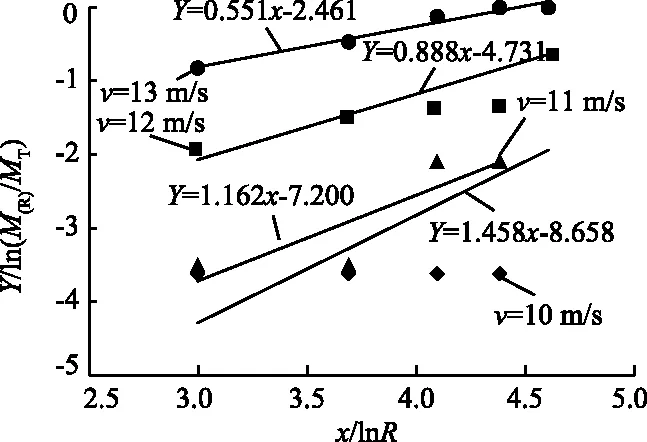
图9 典型砂岩试样的ln[M(R)/MT]-lnR曲线

由图8和图9可知，当冲击速度较低时，各粒径下累计的砂岩碎块质量百分比较低，伴随着冲击速度的增大，各粒径下累计的砂岩碎块质量百分比明显增大，且砂岩碎块的破碎梯度更明显，说明冲击速度较低时，砂岩所承受的冲击载荷较低，岩样吸收的能量较低，无法支撑岩样完全破碎，导致砂岩的破碎程度不明显，冲击速度增大时，岩样吸收的能量增加，远超砂岩的承载能力，致使岩样的破碎程度增大。此外，对砂岩各粒径下累计的碎块质量与粒径数据在双对数坐标中进行线性拟合，得到其线性拟合函数的斜率，从而计算出砂岩碎块的分形维数。典型砂岩试样碎块分形维数与冲击速度的关系如图10所示。

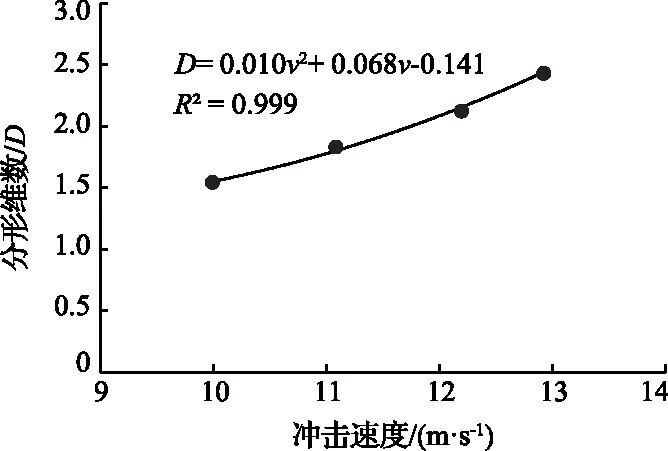
图10 典型砂岩试样碎块分形维数与冲击速度的关系

由图10可知，砂岩碎块的分形维数随着冲击速度的增大呈二次项函数的形式上升，说明冲击载荷作用下砂岩的破碎程度随着分形维数增大而增大。结合不同冲击速度下典型砂岩的破碎宏观形态，可以得出随着冲击速度增大，砂岩所受到冲击载荷增大，岩样吸收的能量增加，岩样的破碎程度越高，相反，冲击速度越低，砂岩碎块的分形维数越小，砂岩的破碎程度越低。因此，可以将分形维数作为描述砂岩破碎特征的定量指标，其可反映砂岩的破碎程度。

4 结 论

1)砂岩的应力-应变曲线整体趋势基本一致，均呈阶段式发展，依次为线弹性上升阶段、非线性振荡起伏阶段和峰后下降阶段。

2)砂岩的动态抗压强度、单位体积吸收能和动态弹形模量均具有冲击速度效应，与冲击速度分别呈幂函数、二次函数、二次函数的关系，均随着冲击速度增大而增大。

3)在冲击载荷的作用下，随着冲击荷载的增大，砂岩的破坏模式由拉伸破坏向拉-剪耦合型破坏转变，破碎程度愈加明显。

4)冲击载荷作用下砂岩碎块的分形维数随冲击速度的增大呈二次函数趋势增大，揭示分形维数D可作为表征砂岩破碎特性的定量指标。