基于演化博弈的政府-煤矿-职工安全监管策略研究

2023-09-27王玉军

煤炭工程 2023年9期

王玉军

(国家能源集团乌海能源有限责任公司老石旦煤矿，内蒙古乌海 016033)

随着我国经济的发展，政府与大众对于生产引发的事故及造成的伤害愈加重视[1-3]。煤作为现代工业的“粮食”，在我国能源结构中占据重要地位[4，5]。为保障煤矿安全生产，相关学者从政府层面提出了完善的安全监管体系。这种监管体系的进步与当下中国经济发展水平相适应，是中国工业安全监管发展的必由之路。在煤矿安全多方监管体系中，煤矿作为不安全生产监管的责任主体，决定了安全监管体系实施的有效性[6]。近年来，煤矿也逐渐认识到安全管理逐渐成为制约我国煤炭产业发展的瓶颈[7]。同时政府在安全监察中的严格程度决定了煤矿是否选择贯彻安全监管。此外，煤矿的策略在一定程度上影响了职工是否选择对不安全行为进行监督，而职工监管不安全生产策略的倾向影响了煤矿贯彻安全监管的选择[8]。在博弈演化的过程中，博弈参与者相互影响，彼此利益互相关联。近些年来，随着安全在生产中的地位不断提高，发生事故以后企业往往会付出巨大的代价。因此煤矿愿意按照安全监管的要求进行安全管理；同时，随着安全管理工作责任制度的完善，提高了政府对于企业安全监管的积极性；另一方面，煤矿提高对职工安全的重视水平，一定程度上决定了职工对于生产中不安全行为是否监督的策略。

演化博弈论针对存在利益影响的参与方内部对抗到相互妥协的过程进行分析，建立演化博弈模型，分析博弈策略演化趋于稳定的过程[9，10]。相关学者对政府、煤矿企业、煤矿内部的安全管理部门以及煤矿职工的安全策略进行了大量研究。李曌[11]通过将博弈论与柯布-道格拉斯生产函数法、相关性分析法相结合，从影响安全投入的角度对政府与矿山、矿山企业内部间的竞争进行了博弈分析。吴春林等人[12]在博弈论的基础上结合安全纽带建立了职工安全纽带缔结的演化博弈动态模型，提出了职工安全行为策略的影响因素。刘纪坤等人[13]构建了煤矿内部领导策略者与监督管理者双群体演化博弈模型，发现安全投入与监管处罚对该模型中各博弈方的策略演化具有显著影响。叶贵等人[14]结合激励相容理论、期望理论与强化理论建立了监管者与工人的全行为动态演化博弈模型，指出奖惩可以引导职工做出不同的安全策略，且奖励的影响度高于罚款。此外，腾云等人[15]结合仿真模拟研究了安全生产下政府、煤矿企业、员工间的博弈演化过程，通过对比不同安全管理模式，提出激励模式较惩罚模式可以激发员工主动选择检举不安全生产的策略。从中不难发现，有关研究在研究煤矿安全管理问题中，通常都是以其中两者为参与者进行演化博弈分析，少量关于煤矿的三方演化博弈通常是以政府与煤矿为主体，再结合职工参与者是否安全生产的策略构建三方演化博弈模型，如图1所示。

本文通过分析安全监管体系下政府、煤矿、职工的博弈关系，构建三方演化博弈模型，分析不同博弈策略对博弈过程和稳定状态的影响，并进行稳定性分析进而提出相应的措施，最终提高多方安全监管体系有效性，为建立规范的宏观多方安全监管体系提供理论依据。

1 演化博弈模型的建立

1.1 问题描述

政府主导、煤矿与职工参与的煤矿安全监管体系是实现煤矿“零事故”目标的重要途径。提升煤矿安全水平要求各参与者履行各自的责任，发挥应有的作用。然而由于在安全上的投入不会直接提高产量，煤矿在安全管理的投入是有限的[16]。煤矿对职工行为的安全监管程度为非理想化。职工在处于经济角度及自身精力分配的考虑，会违反安全规程以达到提高产量以及“省力”的目的。为提升煤矿安全监管力度，政府应急管理部门围绕“制度不执行就是最大隐患”的理念，运用以往工作中积累的经验、对事故进行总结以应对现实的挑战[17]。在政府部门对煤矿进行安全检查，煤矿对内部职工进行检查的情况下，各利益方处于利益的考虑会对检查采取对抗的趋势，那么检查者与被检查者存在博弈。这种博弈随着各方采取的措施力度不同呈现一种非静态的线性演化趋势。煤矿安全监管体系涉及各方利益，但主要是政府、煤矿与职工为主要利益相关者，在实现最大经济效益的前提下要解决煤矿安全生产中存在的问题，妥善处理好各方的既得利益，这样才能保证监管政策的“落地”，切实提高煤矿安全性，保证安全生产[18]。

图1 三方监管体系博弈主体影响关系

1.2 模型假设

假设1：政府监督主体内部由国家监管部门垂直管理地方分部门，地方分部门在国家部门的指导下开展工作，为便于建立模型本文将其统一合并为“政府”博弈主体。政府部门的日常收益为c1，如行政拨款等，行使监督职责所产生的成本为w1，d为政府监管部门未监管获得的潜在收益，e为发生事故导致的经济损失期望。政府监督的概率为x，不监督的概率为1-x，x取值范围是0≤x≤1。

假设2：煤矿遵循安全制度生产情况时的收入为c2，煤矿在安全生产方面的投入为w2，不安全生产导致的处罚及发生事故导致损失的数学期望为f，未监管为煤矿带来的额外收益为g，未监管导致的处罚为h，贯彻监管职责所返还的安全保证金收益为r。煤矿贯彻安全监管概率为y，不贯彻安全监管概率为1-y，y的取值范围为0≤y≤1。

假设3：职工是生产的直接参与者，当身边同事出现不安全生产行为的情况时，其会向煤矿内部安全监管部门举报。对于职工，正常生产时其工资收益为c3，监督制止违法行为的成本为w3，出现事故带来的损失数学期望为m，不安全生产带来的额外收益为n，职工监督获得的奖励为s。职工监督不安全生产行为的概率为z，不监督不安全生产行为的概率为1-z，z的取值范围是0≤z≤1。

基于上述假设，将三方监管演化博弈的主体分别记为政府(A)、煤矿(B)与职工(C)建立三方博弈主体收益矩阵。见表1。

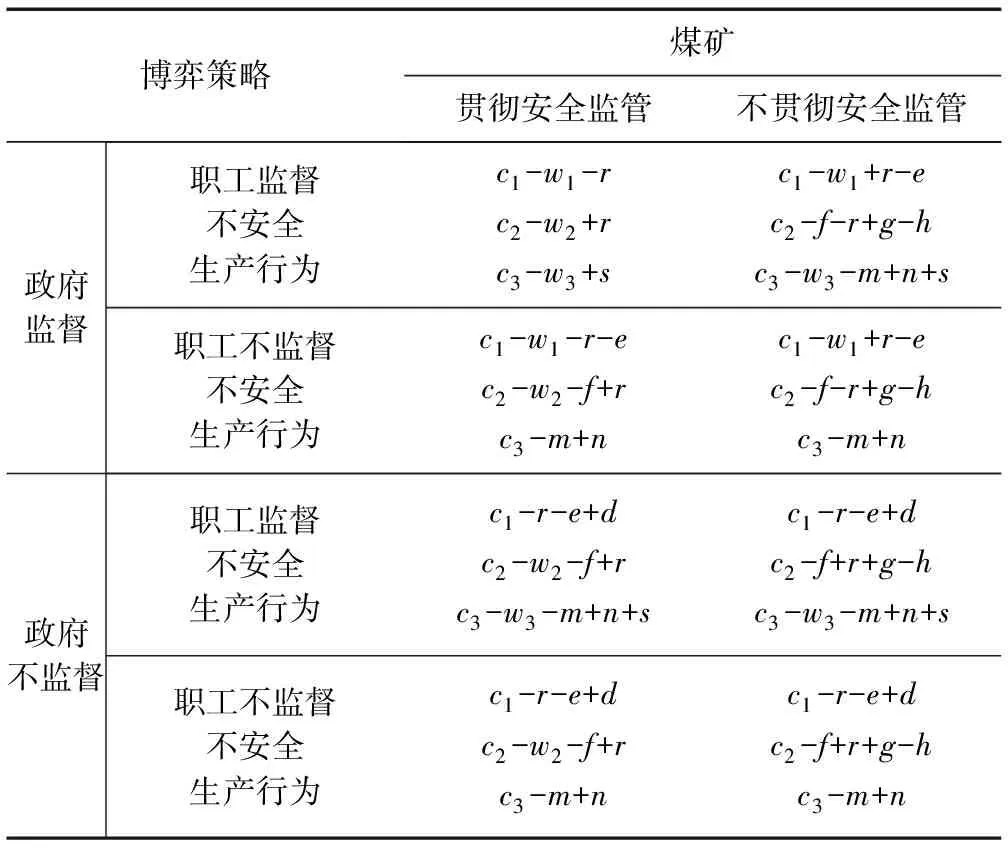
表1 三方博弈主体收益矩阵

2 多重安全监管体系下演化博弈分析

2.1 单博弈主体稳定性分析

多重安全监管体系下政府、煤矿与职工间的博弈模型如图2所示。假设政府监管概率为x，煤矿贯彻安全监管概率为y，职工监管不安全生产行为概率为z。政府安全监管与不安全监管的策略事件集合为N1={A1，A2}政府采取监管或不监管策略的期望收益分别为：

EA1=c1-w1+r-e-2yr+yze

(1)

EA2=c1-r-e+d

(2)

图2 博弈主体策略演化相位图

政府的平均期望收益为：

复制动态方程是由Weibull提出的，策略的变化率代表了博弈主体对于该策略的适用程度[19-21]。据此可以计算政府监管策略的复制动态方程为：

F(x)=x(1-x)[y(ze-2r)+2r-w1-d]

(4)

同理，设煤矿贯彻安全监管或不贯彻安全监管的事件集合为N2={B1，B2}，煤矿贯彻安全监管与不贯彻安全监管策略的复制动态方程分别为：

EB1=c2-w2+r-f+xzf

(5)

EB2=(x+1)(c2-f+g-h)+(1-x)r

(6)

煤矿的平均期望收益为：

y(-w2+xzf)+(c2-f+r)

(7)

煤矿贯彻监管策略的复制动态方程为：

y(1-y)[x(zf-c2+f-g+h+r)-w2-g+h]

(8)

设职工监督不安全生产行为或不监管不安全生产行为的事件集合为N3={C1，C2}，同理可得职工监督不安全行为与不监督不安全行为的复制动态方程分别为：

EC1=xy(m-n)+c3-w3-m+n+s

(9)

EC2=c3-m+n

(10)

职工的平均期望收益为：

职工监管不安全生产策略的复制动态方程为：

将式(4)、式(8)及式(12)组成多重安全监管体系演化博弈的系统如下：

2.2 单博弈主体稳定性分析

2.2.1 政府角度演化稳定性分析

政府的策略呈稳定状态时需要满足条件F(x)=0，∂F(x)/∂x<0。根据公式(4)求偏导可得：

F′(x)=(1-2x)[y(ze-2r)+2r-w1-d]

(14)

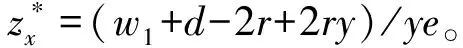
2.2.2 煤矿角度演化稳定性分析

煤矿的策略呈稳定状态时需要满足条件F(y)=0，∂F(y)/∂y<0。根据公式(8)求偏导可得：

F′(y)=(1-2y)

[x(zf-c2+f-g+h+r)-w2-g+h]

(15)

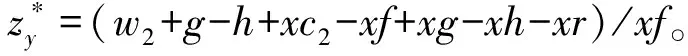
2.2.3 职工角度演化稳定性分析

职工角度的策略达到稳定状态需满足：F(z)=0，∂F(z)/∂z<0。对公式(12)求偏导可得：

F′(z)=(1-2z)[xym-xyn+s-w3]

(16)

3 三方博弈系统演化稳定性分析

从对称视角对政府、煤矿及职工三方监管博弈模型进行演化稳定策略及稳定状态分析。根据上文分析可以得到多方博弈模型Jacobi矩阵。策略均衡点需满足条件F(x)=F(y)=F(z)=0，8个均衡点分别是E1(0，0，0)，E2(1，0，0)，E3(0，1，0)，E4(0，0，1)，E5(1，1，0)，E6(1，0，1)，E7(0，1，1)，E8(1，1，1)。当矩阵所有特征值均小于0时均衡点同时为稳定点，讨论均衡点的渐近稳定性。Jacobi矩阵为：

其中：

J11=(1-2x)[y(ze-2r)+2r-w1-d]

J12=x(1-x)(ze-w1-d)

J13=x(1-x)[y(e-2r)+2r-w1-d]

J21=y(1-y)[zf+f-c2-2g+2h+r-w2]

J22=(1-2y)[x(zf-c2+f-g+h+r)-w2-g+h]

J23=y(1-y)[x(f-c2+f-g+h+r)-w2-g+h]

J31=z(1-z)[y(m-n)+s-w3]

J32=z(1-z)[x(m-n)+s-w3]

J33=(1-2z)[xy(m-n)+s-w3]

(18)

将各均衡点带入式(18)，可分别得到不同均衡点的特征值λ1、λ2、λ3见表2。

表2 三方博弈各均衡点特征参数

三方博弈系统稳定性见表3。情景1：w1+d<2r，f+2h+r

情景2：w1+d

情景3：w1+d<2r，w3

情景4：w1+d<2r，w2+g

表3 三方博弈系统稳定性

4 安全监管体系改进措施

4.1 煤矿主管部门改进措施

煤矿主管部门安全监督策略行为与职工的策略有关。在满足相应条件的情况下当职工选择对不安全行为进行监督时，煤矿主管部门在外界压力的作用下逐渐选择提升对于煤矿安全生产的监管力度；当职工选择对不安全生产行为不监督时，煤矿主管部门策略逐步向不监管演化。当对职工策略的参数进行调整时可以有效提高政府的监督效率。调整参数如下：提高发生事故以后导致的损失期望，如上调事故发生以后对于相关事故责任人的追责力度；提高煤矿缴纳安全保证金r的额度，保证金额度的提高有利于提升政府重视程度；减少不安全生产给政府带来的额外收入，包括打击受贿，降低政府财政与煤矿产值关联程度；应当引入新技术，精简监管机构，在保证监管强度不变的前提下减少经费支出。

4.2 煤矿改进措施

4.3 职工改进措施

职工是否选择监管与政府监管的策略有关。当政府倾向于不监管的策略多一些的时候，职工出于获取更多收益的目的，且在不监管的环境影响下会对不安全行为采取漠视的态度，职工策略向不监管的方向演化。而煤矿在保证金以及不安全生产带来的损失等情况的影响下会选择贯彻安全监管的策略；而在政府安全监管策略多一些的情况下，即使煤矿选择不监管的策略，职工也会倾向于选择安全监管就策略。影响职工安全策略的参数有：提高不安全生产对其带来的损失，降低不安全生产带来的收益，降低监督过程中职工所付出的成本，提高职工监督不安全生产行为所得到的奖励。