双转子风力机气动建模与控制仿真研究

张文广, 骆伟健, 孙嘉壕

(华北电力大学 控制与计算机工程学院,北京 102206)

随着风力发电技术的快速发展,亟需进一步提高风力机的风能利用率。一方面,传统风力机通过增大叶片尺寸的方式,提高了风能利用率,但也会给风力机造成很大的疲劳载荷与极限载荷,给设计、生产和运维带来巨大挑战。另一方面,在不改变叶片尺寸的前提下,采用双转子风力机结构也能提高风能利用率。根据Newman动量理论[1],双转子风力机的功率系数最大约为64%,高于由Betz理论[2]得到的单转子风力机风能利用系数的极限值59.3%。使用双转子结构既可避开长叶片的设计制造,又能提高风能利用率。

近年来,国内外对双转子风力机的研究主要集中在物理结构分布和气动特性分析等方面。Jung等[3]对反向旋转双转子风力机进行了数值计算,研究表明副转子叶片尺寸为主转子50%时,风能利用率可达50%。Kanemoto 等[4]设计了3种不同主副转子半径比的双转子风力机模型,结果表明采用前大后小的主副转子尺寸设计能够显著提升双转子风力机风能利用率。孙义鸣等[5]搭建了同向旋转双转子风力机模型,研究了转子间距和相位角对风力机功率的影响,结果表明副转子功率随转子间距增大而先增大后减小,在相位角为30°时总功率达到最大值。Kumar等[6]搭建和测试了双转子风力机模型,并与基于CFD的传统单转子风力机的空气动力学性能进行了比较,结果表明采用反向旋转的双转子风力机功率增加约10%。Habash等[7]对小型双转子风力机进行了风洞研究,双转子风力机的功率可比单转子风力机提升60%,并能够在保持风力机性能的同时降低切入风速。Shen等[8]对双转子风力机的性能进行了数值研究,结果表明主副转子之间的间距对功率和风载荷波动有较大影响,在较高风速下双转子风力机的年能源产量可比单转子风力机提升约43.5%。杨瑞等[9]研究发现副转子能够转化主转子叶根位置的部分动能,提高双转子风力机整机功率。Ozbay等[10]通过风洞实验研究了双转子同向旋转与反向旋转时的尾迹和气动特性,对比发现采用反向旋转形式能够捕获更多风能。上述研究表明,当副转子叶片尺寸为主转子的50%～60%[3-4]、异侧设置的主副转子间距为0.25D[5,8,11](D为主转子叶轮直径)且主副转子旋转方向为反向旋转[3,10]时,能够有效提高双转子风力机的风能利用率。但针对全风速工况尤其湍流风况下双转子风力机发电功率的自动控制,上述文献尚没有研究。

基于以上研究,笔者以NREL 5 MW和WindPACT 1.5 MW风力机转子为例,在Matlab/Simulink中搭建了双转子风力机的气动与控制仿真模型。基于自由涡尾迹法(Free Vortex Wake, FVW)计算了流场分布。进而研究了双转子风力机的功率特性以及模糊控制策略在其功率方面的控制效果。

1 研究对象

FAST是由NREL开发的综合性气弹仿真开源平台,经过GL认证其仿真结果具有较高可信度[12]。基于主副转子叶片尺寸、转子间距与旋转方向等因素,课题组对FAST进行了二次开发,以5 MW与1.5 MW风力机转子为基础,搭建了双转子风力机的气动与控制仿真模型。

1.1 双转子风力机的主要参数

双转子风力机的主转子采用5 MW参考风力机转子,副转子采用1.5 MW参考风力机转子。其主要参数分别见表1[13]和表2[14]。

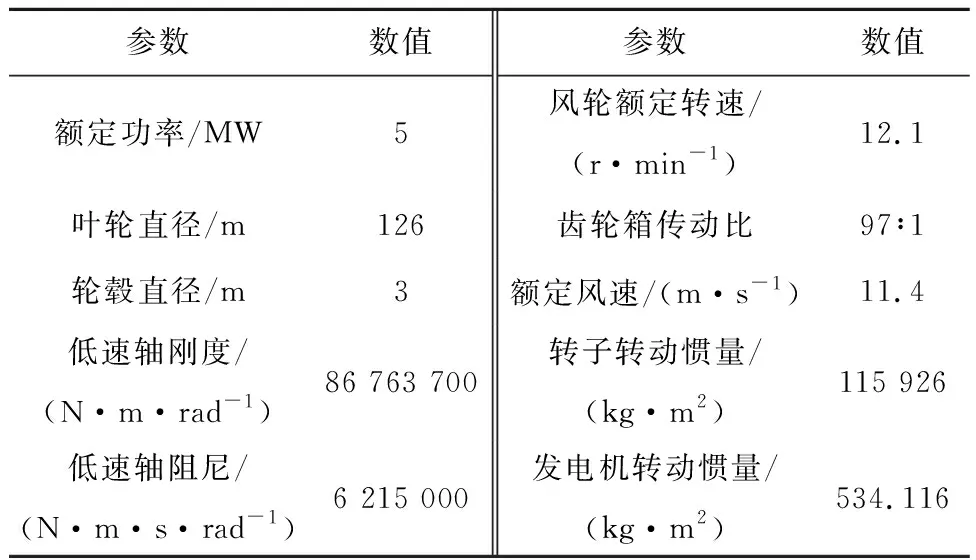
表1 NREL 5 MW风力机转子参数

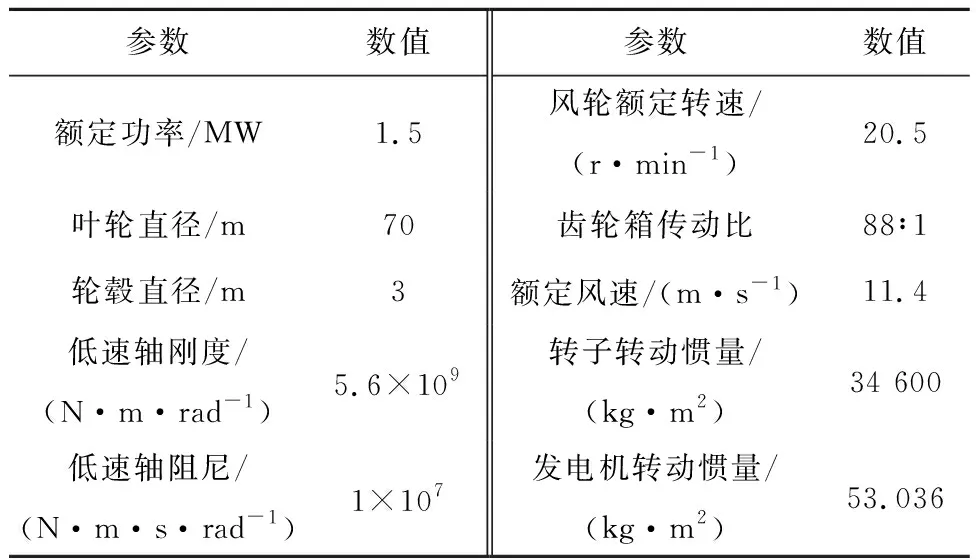
表2 WindPACT 1.5 MW风力机转子参数

1.2 双转子风力机

位于上风向的5 MW风力机转子作为主转子,位于下风向的1.5 MW风力机转子作为副转子。二者采用反向旋转的形式,分别设置在机舱前后。来流风速用Vrel表示,主转子与副转子之间的转子间距用d表示,本文采用d=0.25D,其中D为主转子叶轮直径。由此构成的双转子风力机示意图与其内部简化结构示意图,分别如图1和图2所示。

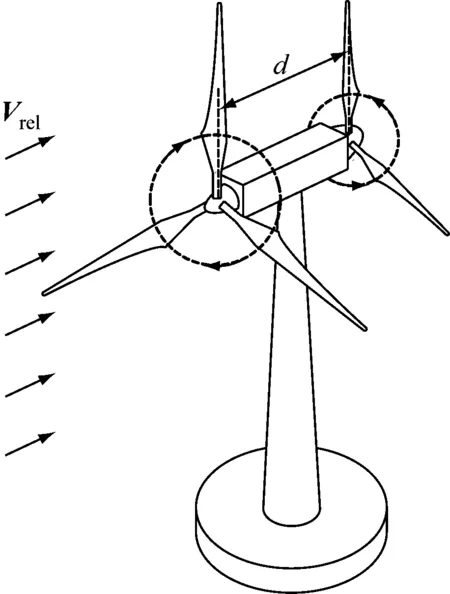
图1 双转子风力机示意图

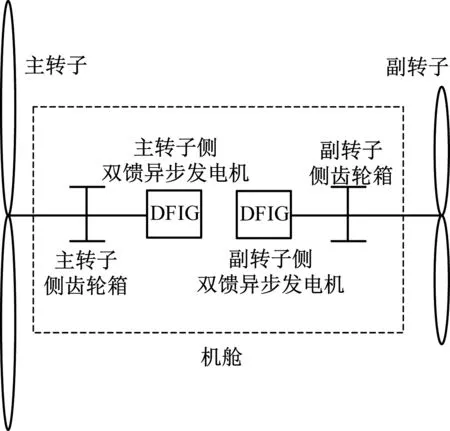
图2 双转子风力机内部简化结构示意图

2 双转子风力机建模

本文的双转子风力机模型主要分为气动、塔影效应、传动链与发电机模型。

2.1 气动模型

单转子风力机气动模型通常采用叶素动量理论(Blade Element Momentum Method, BEM)进行建模,运算速度快,但精度不高。由于双转子风力机的气动特性复杂,尤其是主转子尾流对转子间流场分布的影响,BEM方法难以满足双转子风力机气动模型精度要求。FVW相较BEM引入了对尾迹流场的仿真,具有较高精度,相较CFD方法将尾迹简化为可以自由运动的涡元,减少了计算量[15]。笔者基于FVW建立了双转子风力机气动模型,采用1/4处弦长的附着涡线代替叶片,每段附着涡环量由对应叶素的气动特性确定。在尾迹坐标系中,FVW偏微分形式的控制方程可表示为:

(1)

式中:r为尾迹流场中涡线控制点的位置矢量,m;Ψ为叶片方位角,rad;ζ为尾迹寿命角,rad;Ω为风轮转子转速,rad/s;Vrel为无穷远处来流风速,m/s;Vind为流场中所有涡线对该控制点诱导速度的总和,m/s;t为时间,s。

时间步进FVW[15]重点在于能够获得非定常流场中随时间变化的尾迹几何形状和气动特性,迭代计算步骤如下。

第1步,初始尾迹采用等螺距的圆柱形刚性尾迹。

第2步,利用BEM计算叶片的入流特性,并计算第i个叶素的附着涡环量Γb:

(2)

式中:Wi为合速度,m/s;Cl为升力系数,采用线性插值法从翼型数据表中求得;ci为叶素控制点处翼型弦长,m。

第3步,计算尾迹涡环量Γt和脱体涡环量Γs:

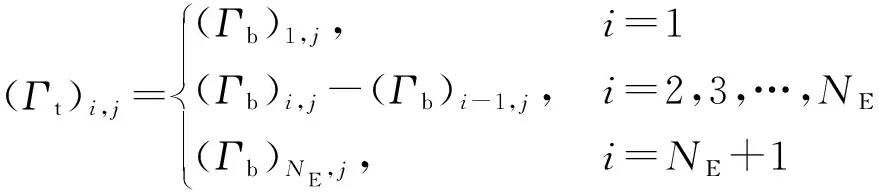
(3)

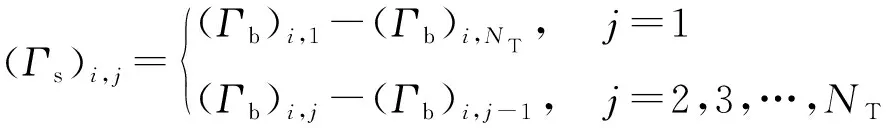
(4)

式中:j为不同的方位角;NE为叶素数目;NT为方位角数目。

第4步,利用涡模型计算尾迹各节点的诱导速度,其中,涡模型采用Vatistas等[16]给出的集中涡周向诱导速度Vθ(r)型:

(5)

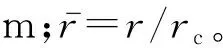
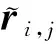
(6)

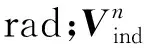
第6步,采用校正步校正预估步尾迹形状,其中,校正步ri,j:

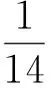
(7)

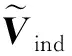
第7步,当方位角不是2π的整数倍时,返回第2步继续步进;当方位角是2π的整数倍时,计算该时刻尾迹形状与上一周期时刻尾迹形状的几何残差,若几何残差大于10-4,返回第2步继续步进,否则尾迹形状收敛,计算完成。

2.2 塔影效应模型

由于副转子位于下风向,需要考虑塔筒对气流的阻碍,即塔影效应。采用Powles[17]塔影效应模型,计算副转子受塔影效应减小的风速比例uTwrShadow:

(8)

式中:Cd为塔筒阻力系数;xTwr为轴向相对于塔架中心的坐标;yTwr为侧向相对于塔架中心的坐标。

2.3 传动链模型

风力机的传动系统可以看成由有限个惯性单元、弹性单元和阻尼单元组成的系统。在双转子风力机实际设计中,传动系统能够实现解耦,因此本文采用了弹簧-阻尼-质量系统的动力学模型[18],其中齿轮箱使用一级行星二级平行轴齿轮箱,建立的双传动链的动力学模型如下:

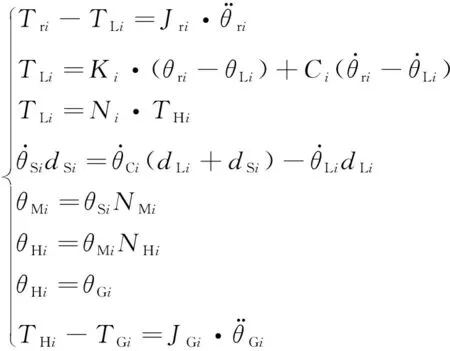
(9)

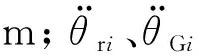
2.4 发电机模型

双馈异步发电机的定、转子均能与电网进行功率交换。由于转子绕组的电源频率由变频器自动调节,当发电机转速变化时可保持电流频率与电网一致,实现机组变速恒频控制。

受传动系统解耦影响,双转子风力发电机可简化成2台双馈异步发电机。采用其等效简化模型,即一阶动态模型表示:

(10)

(11)

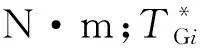
3 双转子风力机流场计算

基于时间步进FVW方法,本文计算了稳态风况与湍流风况下双转子风力机中主转子的尾迹分布,进而得到了副转子旋转截面的流场分布。FAST中流场网格是由TurbSim[19]设定的,为适应后续FAST仿真,网格示意图如图3所示。

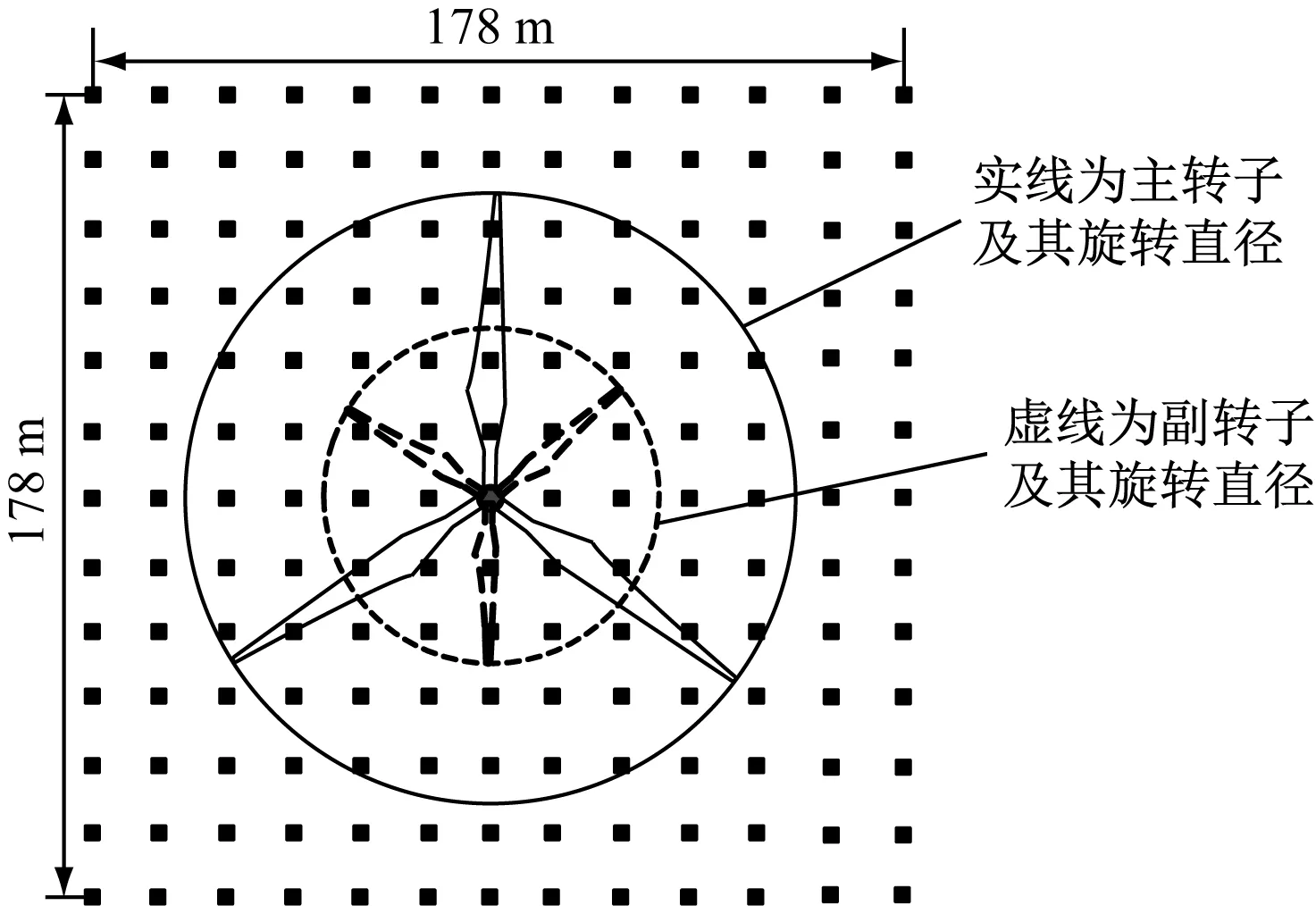
图3 网格示意图

3.1 流场计算对比分析

CFD一般用于双转子风力机静态数据分析。本文FVW方法采用与CFD中相同的工况设置:来流风速9 m/s、风向与双风轮机舱轴线夹角为0°、主转子桨距角0°及主转子转速9.4 r/min,对双转子风力机流场进行静态数据对比。CFD计算的速度云图如图4所示。FVW计算的尾迹图如图5(a)所示。以同一时刻副转子旋转截面轮毂高度处为中心,取任意方向4个格点位置(本文取垂直向上),共5个位置的风速数据进行比较,不同位置处的风速相对误差绝对值见表3。

图4 来流风速为9 m/s时CFD速度云图

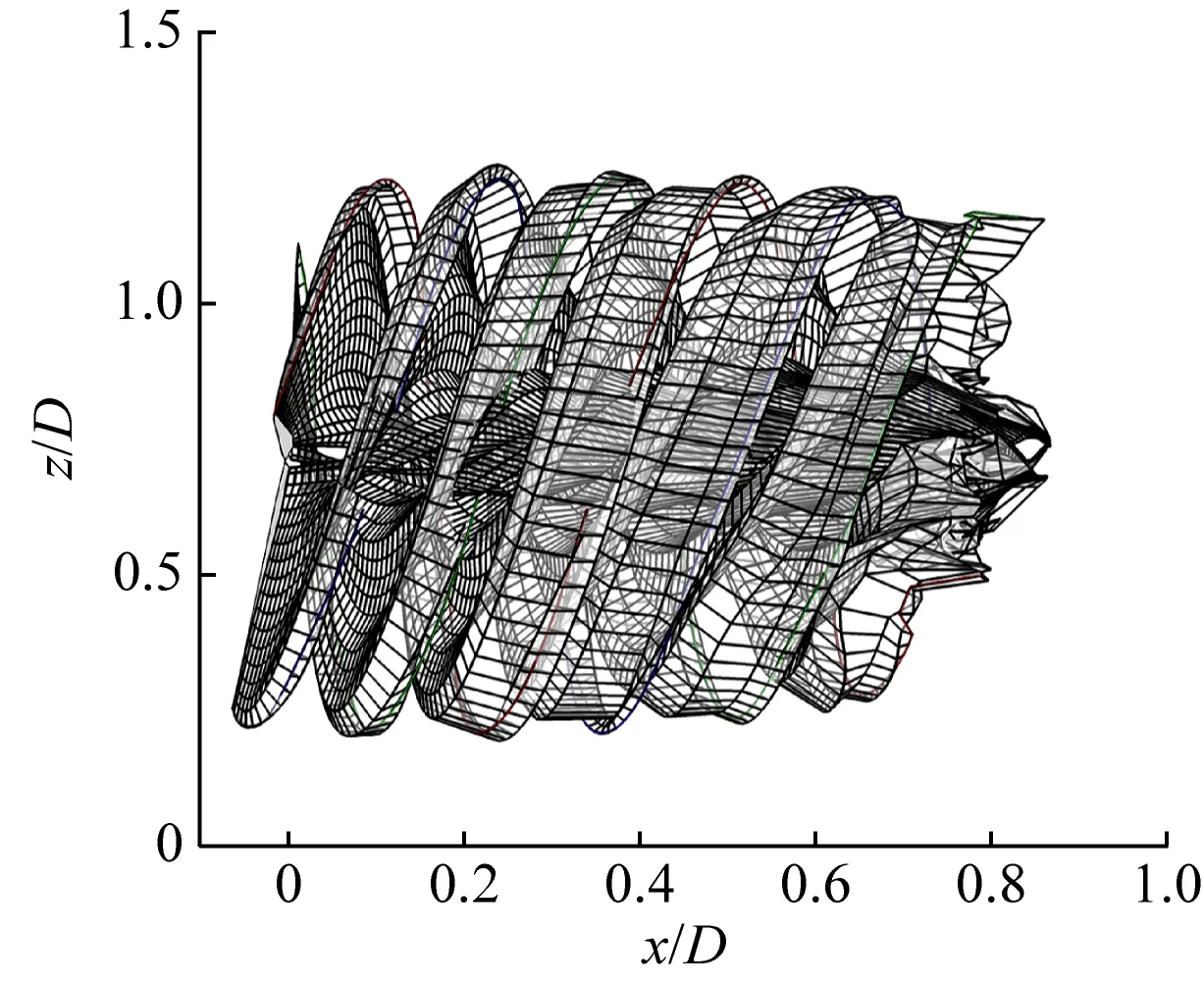
(a) Vrel=9 m/s时的主转子尾迹(t=12 s)

表3 副转子旋转截面不同位置处的风速相对误差绝对值

由图4、图5(a)和表3可知,与CFD计算结果相比,副转子旋转截面不同位置处的风速相对误差绝对值均在10%以内,所搭建的气动模型精度较高且运算时间短。

南京体育学院休闲体育专业只要以课程形式出现的民间体育项目都有特定的课程大纲，并且每个课程大纲各不相同。在学时分配、课程内容、考核方式方面也存在差异。虽然南京体育学院民间体育课程开发时间不长，处于初级阶段，但是课程大纲也是根据学校现有的场地、器材和师资情况来安排的，教学过程也处在一个不断学习、不断完善、不断创新的过程，为了使民间体育课程更加科学化、具体化、现代化，在教材方面，三个项目都没有固定的教材。

3.2 稳态风况下主转子尾迹及主副转子轮毂处风速

在稳态风况下,主转子尾迹及主副转子轮毂处风速仿真分为3种情形:来流风速为9 m/s且主转子桨距角为0°;来流风速为11.4 m/s且主转子桨距角为0°;来流风速为15 m/s且主转子桨距角为10.45°。风向与双风轮机舱轴线夹角均为0°,仿真时间均为300 s。上述3种稳态风况下的主转子尾迹及主副转子轮毂处风速如图5所示。主转子尾迹图的坐标轴中,x方向为从主转子旋转截面水平指向副转子旋转截面,z方向为竖直向上。稳态风况下,副转子轮毂高度处流场的湍流强度见表4。

表4 稳态风况下副转子处流场的湍流强度

从图5可以看出,在稳态风况下,副转子流场受主转子尾迹影响,其轮毂高度处风速低于主转子轮毂高度处风速,该风速会在某一风速值附近周期变化,振幅约为±0.5 m/s。由表4可知,稳态风况下副转子处流场的湍流强度随来流风速的增大而减小。

3.3 湍流风况下主转子尾迹及主副转子轮毂处风速

在湍流风况下,主转子尾迹及主副转子轮毂处风速仿真分为2种情形,即平均来流风速分别为9 m/s和15 m/s。当来流风速低于11.4 m/s时,主转子桨距角保持在0°;当来流风速高于11.4 m/s时,主转子桨距角动态变化,保持主转子功率为额定功率。来流风的湍流强度均为5%,风向与双风轮机舱轴线夹角均为0°,仿真时间均为300 s。上述2种湍流风况下的主转子尾迹及主副转子轮毂处风速如图6所示。湍流风况下,分析特定时间段副转子处流场的湍流强度,结果见表5。

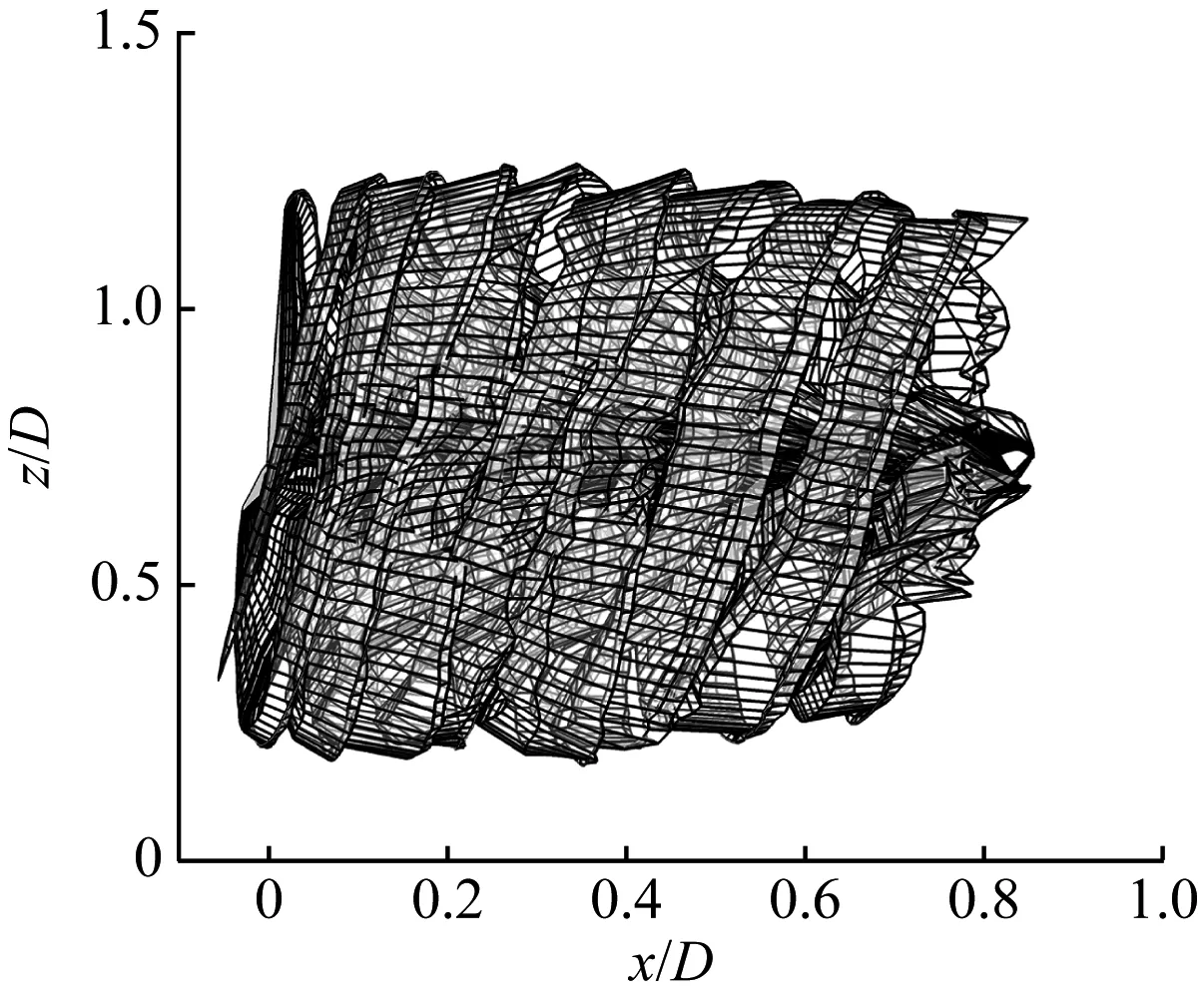
(a) 平均风速为9 m/s时的主转子尾迹(t=22 s)

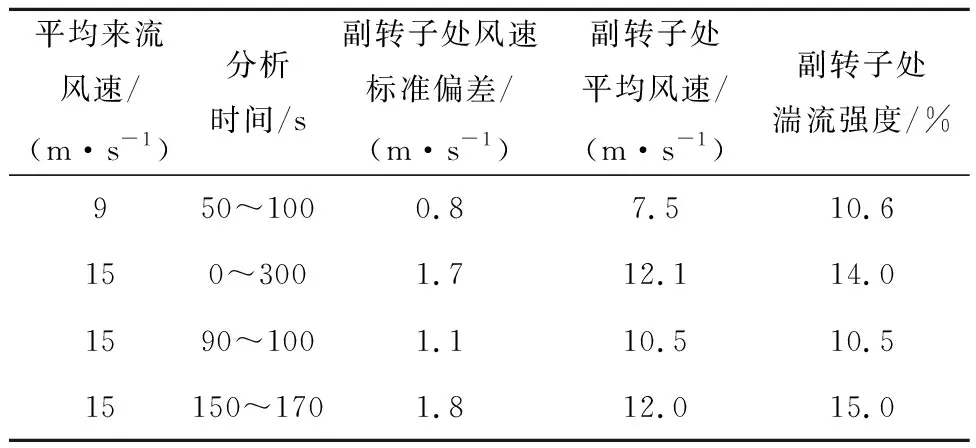
表5 湍流风况下副转子处流场的湍流强度

从图6可以看出,相比稳态风况,湍流风况下的主转子尾迹位置更加凌乱,副转子轮毂高度处风速与主转子轮毂高度处风速变化趋势基本一致。由表5可知,在低风速段,副转子旋转截面处流场受主转子影响,其湍流强度会强于主转子处;在高风速段,随着风速大小的变化,主转子变桨执行机构相应改变其桨距角。主转子尾迹受来流风况与自身变桨共同影响,从而使副转子旋转截面处的湍流情形变得更加复杂。

4 双转子风力机运行控制仿真

基于模糊控制对双转子风力机进行了仿真,研究了不同风况下模糊控制策略在双转子风力机功率控制方面的效果,并计算了稳态风况下双转子风力机的风能利用率。在Matlab/Simulink中搭建的双转子风力机的气动与控制仿真模型如图7所示。

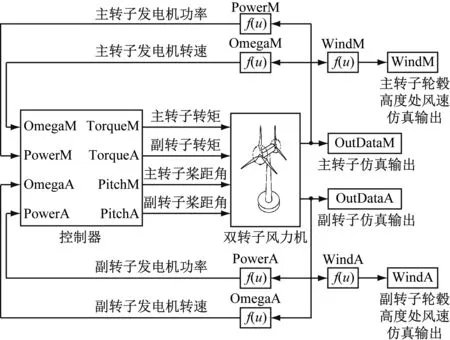
图7 双转子风力机的气动与控制仿真模型

4.1 稳态风况下双转子风力机功率仿真及风能利用率

基于上文稳态风况的流场分布,主副转子变桨控制均采用模糊控制。稳态风况下双转子风力机功率曲线如图8所示。在低风速段,不同稳态风况下双转子风力机的功率特性见表6。

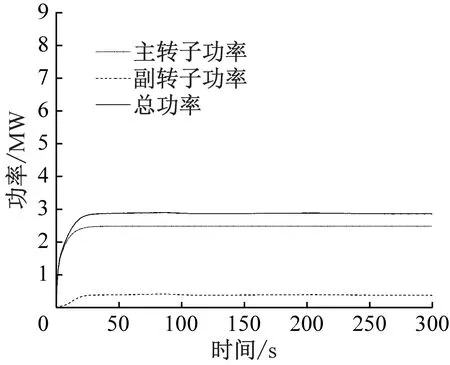
(a) Vrel=9 m/s

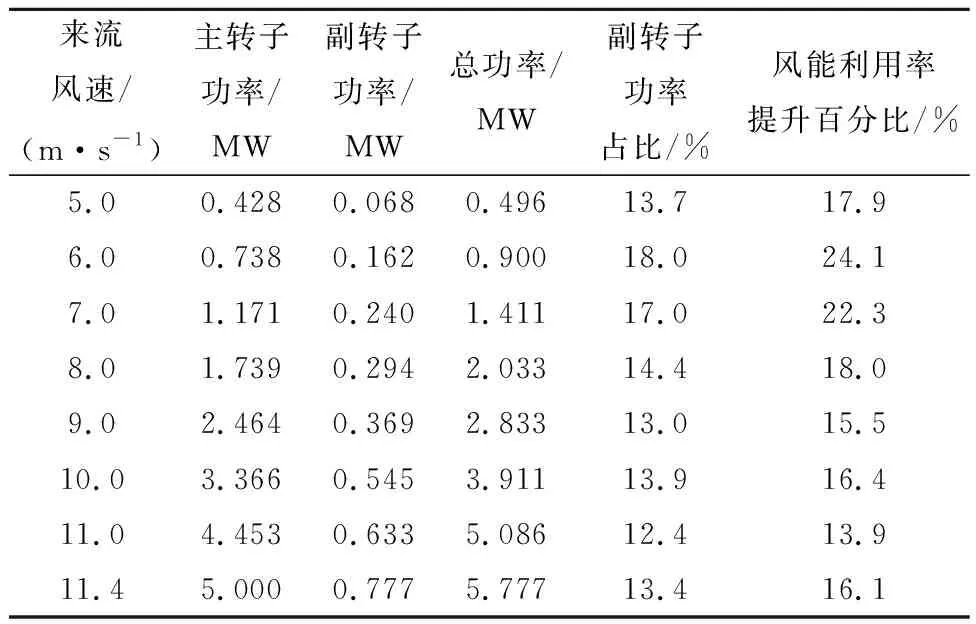
表6 低风速段双转子风力机功率特性

由图8和表6可知,在低风速段,随着风速增大,双转子风力机总功率也增大,副转子功率占比均高于12%。副转子功率占比与风能利用率随着风速的增大均先增大后减小。与5 MW参考风力机相比,风能利用率可提高约24%。

4.2 阶跃风况下双转子风力机功率仿真及副转子控制策略对比

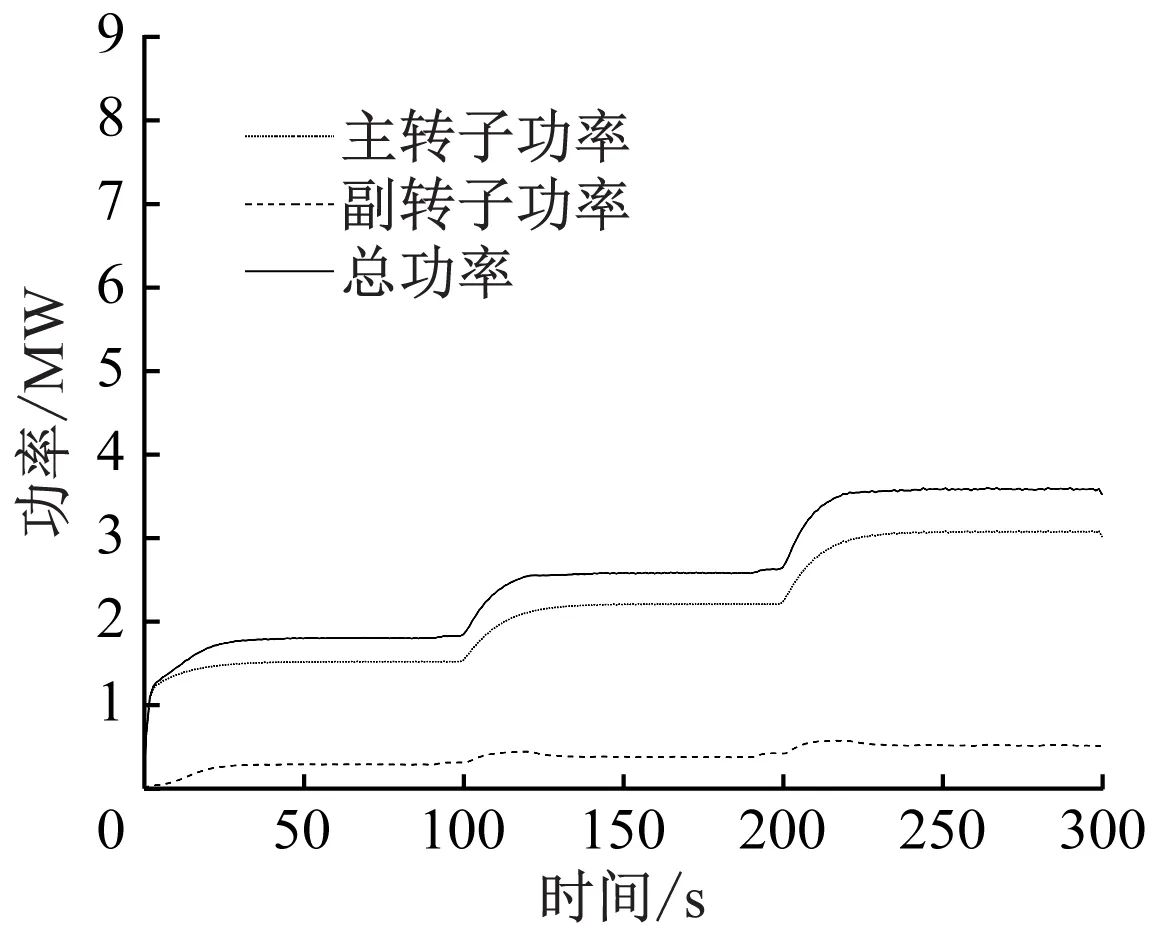
(a) 来流风速从8 m/s到10 m/s

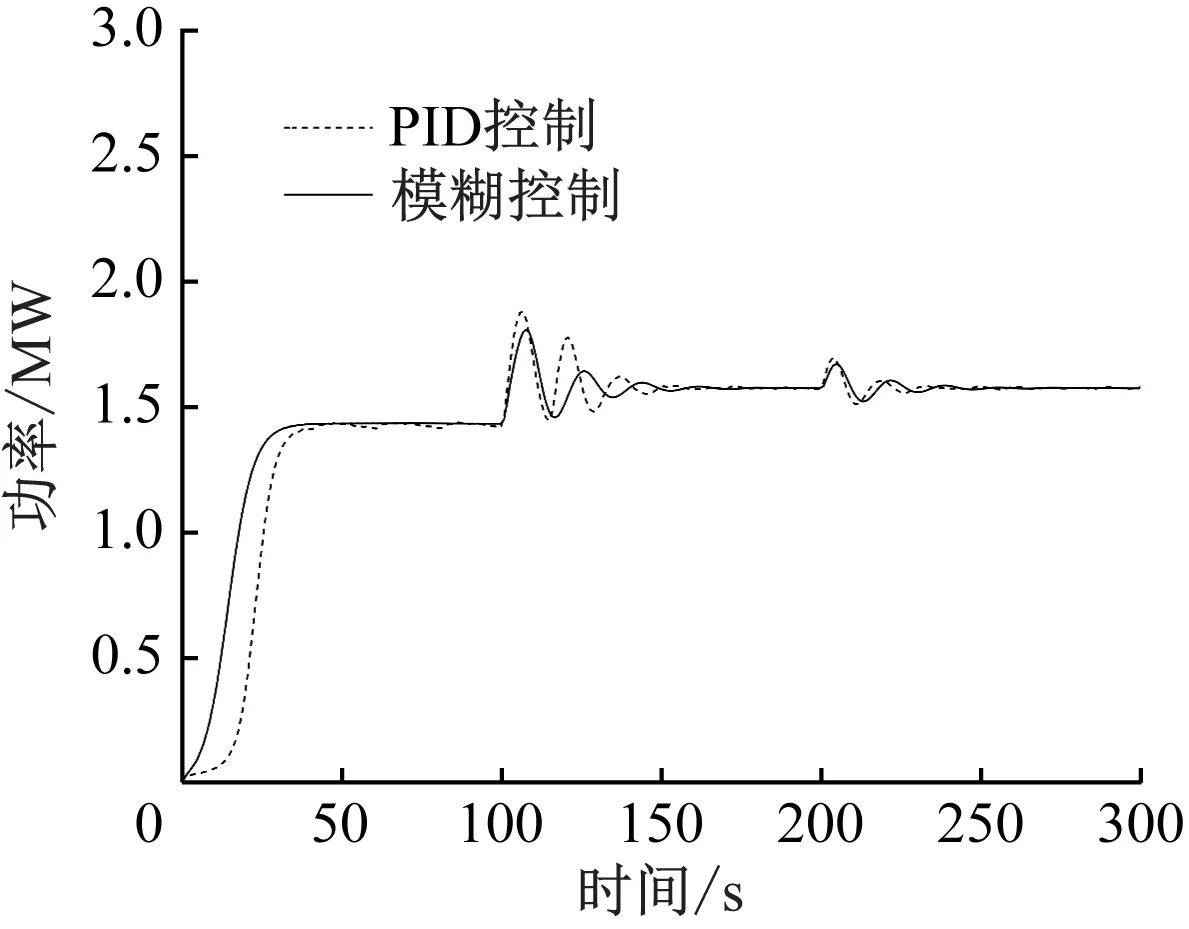
图10 高风速段时不同控制策略下的副转子功率曲线

表7 高风速段副转子功率的动态特性

由图9可以看出,在低风速段控制策略能够使双转子风力机获得最佳风能利用率;高风速段来流风速稳定后,控制策略可使双转子风力机功率保持稳定。由图10和表7可知,阶跃风况下模糊控制策略能够有效改善双转子风力机功率的动态响应。

4.3 湍流风况下双转子风力机功率仿真及副转子控制策略对比

基于上文湍流风况的流场分布,主副转子变桨控制均采用模糊控制。双转子风力机中主副转子功率曲线与副转子控制策略对比曲线分别如图11和图12所示。高风速段副转子功率的超调量见表8。

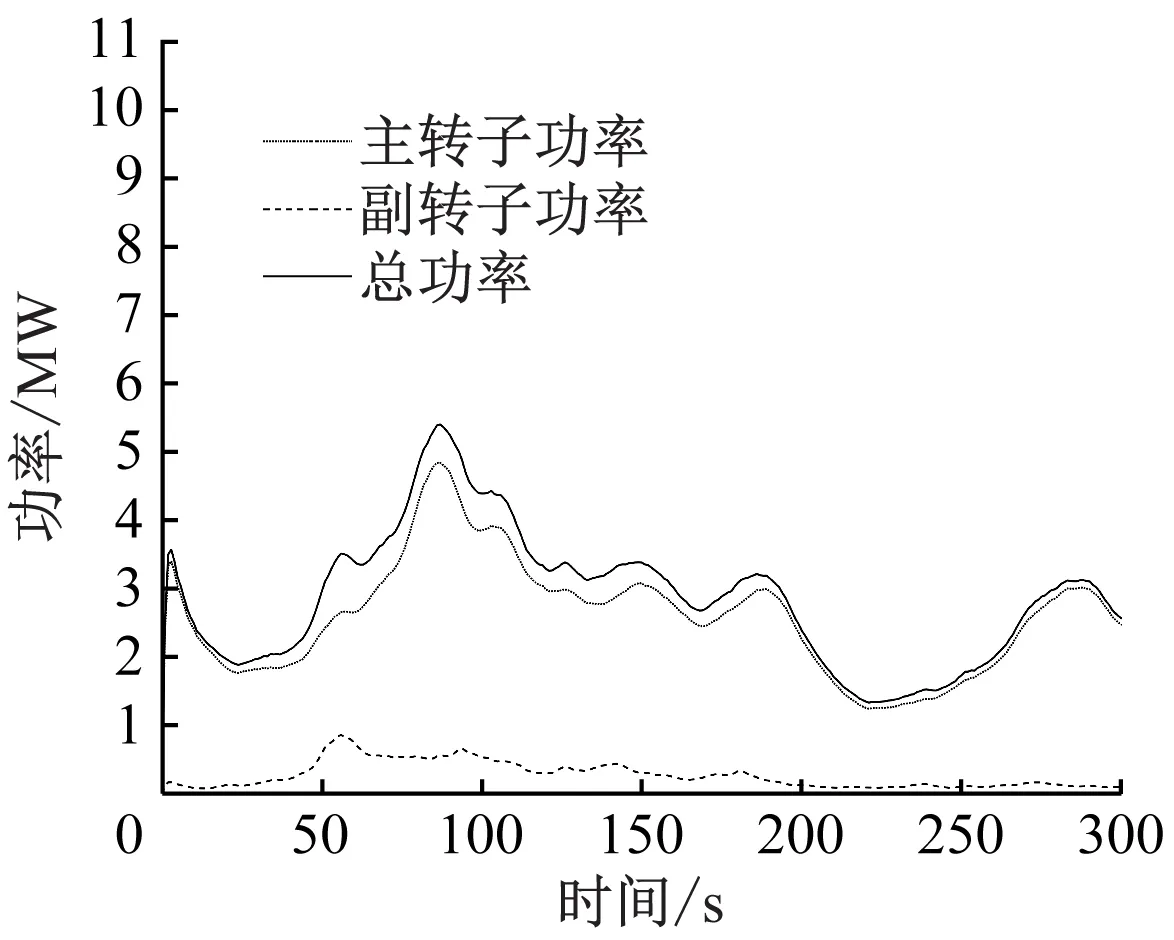
(a) 平均风速为9 m/s

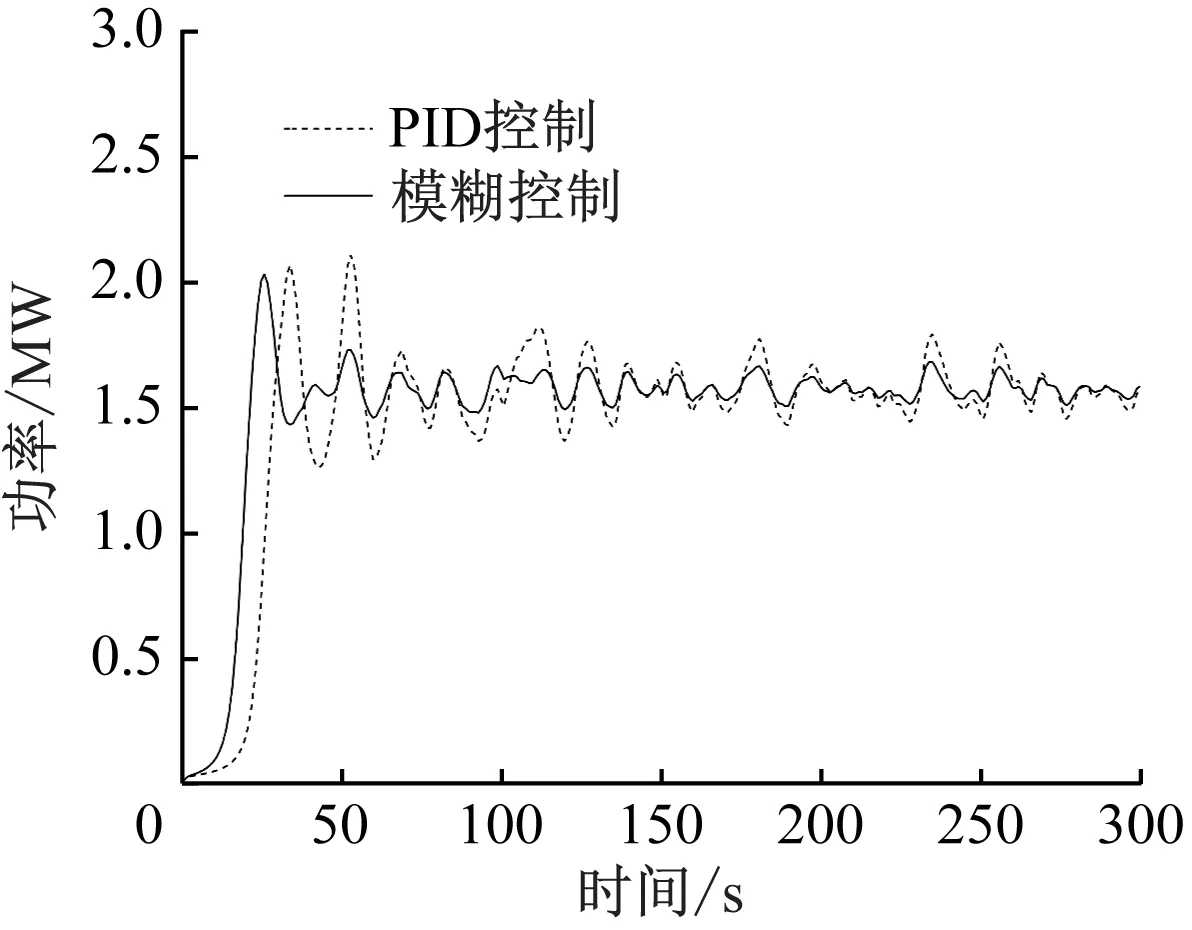
图12 平均风速为15 m/s时不同控制策略下的副转子功率曲线

表8 高风速段副转子功率的超调量

从图11可以看出,在低风速段,即使风速较小,副转子仍可以利用主转子尾迹中的风能,流场的湍流强度虽有所增强,控制策略仍能使双转子风力机获得最佳风能利用率;在高风速段,控制策略能够使主副转子功率保持在额定功率。由图12和表8可知,湍流风况下模糊控制能够有效抑制双转子风力机的功率波动。

5 结 论

(1) 在来流风速为9 m/s、主转子桨距角为0°、风向与双风轮机舱轴线夹角为0°及主转子转速为9.4 r/min的稳态风况下,分别以FVW与CFD方法进行双转子风力机的气动计算,比较相同位置处的风速数据,结果表明FVW的相对误差绝对值小于10%,且运算时间更短,验证了FVW在双转子风力机流场计算方面的快速性与准确性。

(2) 在低风速段,随着风速增大,双转子风力机总功率也增大。副转子功率占比与风能利用率随着风速的增大均先增大后减小。相比5 MW参考风力机,双转子风力机风能利用率可提高约24%。

(3) 在高风速段,主转子尾迹受来流风况与自身变桨共同影响,使副转子旋转截面处的湍流情形变得更加复杂。与PID控制策略相比,双转子风力机采用模糊控制策略能够有效改善功率控制的动态响应和抑制功率波动。