千米深井井壁与围岩共同承载理论研究及应用

宋 刚，周晓敏

(1.中煤天津设计工程有限责任公司，天津 300120；2.北京科技大学 土木与资源工程学院，北京 100083)

随着煤炭开采活动的进行，我国浅部煤炭资源量逐渐减少。在东部地区，有许多煤质较好的煤炭资源埋深超过1000 m，需采用超深立井开拓；在西部地区，也有许多适宜建设特大型矿井并且煤质较好的煤炭资源埋深超过600 m，不适宜采用斜井开拓，因此深立井建设的重要性越来越明显。

据统计，到2020年底，国内已开工的千米深井约87个，其中煤炭行业约52个。随着埋深加大，千米深井的井筒将面临深厚冲积层、深厚复杂岩层、高地压、高水压等问题[1-3]，因此合理的井筒设计成为了千米深井建设关键。针对超千米深井井筒的监测[4，5]和井壁设计[6-10]成为了井筒研究的重点，有学者从弹性、弹塑性、塑性设计理论方面[11-13]对冻结壁进行了研究，还有学者从井壁应力及位移场方面[14-16]开展了深入分析。

本研究为解决超千米深井建设中遇到的井壁厚度无法合理计算难题，以磁西一号矿井超千米深井井壁结构为工程背景，从“井壁与围岩共同承载”理论出发，分析超千米深井井壁与围岩相互作用机理，建立统一力学模型，推导了超千米深井井壁厚度计算表达式，并应用于磁西超千米副立井的设计中，最终取得了良好的经济效益。

1 工程概况

磁西一号矿位于河北省峰峰矿区，副井与风井场地联合布置。副立井设计净直径8 m，井深1341.6 m；回风立井设计净直径7 m，井深1305 m。根据井筒检查孔显示，井筒先后揭露了新生界第三、四系冲积地层189 m，中生界三叠系岩层331 m，古生界二叠系上统岩层798.15 m、下统岩层41.85 m。

岩层主要以泥岩和砂岩为主，主要含水层为二叠系山西组砂岩含水层、石盒子组砂岩含水层、石千峰组砂岩含水层和新生界松散含水层。地层走向为N30°～50°E，倾向SE，倾角为18.6°。井筒附近有两个断层，分别为CF16正断层和CF15正断层，倾角一般60°～70°，落差70～80 m。

2 传统理论设计方法

2.1 传统井壁设计特点

现行井筒设计主要根据《煤矿立井井筒及硐室设计规范》，该规范中井壁设计的基础理论是基于平面应变模型推导的厚壁圆筒理论，该理论公式为：

式中，t为井壁厚度，m；rn为井筒净直径，m；P为作用在井壁上的设计荷载，MPa；fs为井壁材料设计强度，MN/m2。式(1)也被称为拉麦公式，其关键参数有两个，分别是作用在井壁上的设计荷载P和井壁材料强度fs，其中设计荷载值P的取值历来是井壁厚度计算关键[17]。

传统设计中针对基岩段设计荷载P的取值，主要是应用秦氏公式进行计算[18]，然而在深立井井筒井壁设计荷载计算中，如沿用秦氏公式计算，所得井壁设计载荷将急剧增大，导致井壁厚度过大并趋于不合理。为解决上述问题，规范中又提出了修正的秦氏计算公式，即当存在较厚坚硬稳定岩层时，可认为该坚硬岩层压力对下方岩层压力不再产生影响。

2.2 传统井壁设计局限性

在超千米深立井井筒工程设计中，如选用秦氏公式将导致设计荷载过大；如选用修正秦氏公式，则难以选择到合适的坚硬稳定岩层计算设计荷载，且岩层的选择主观性过大，因此传统设计理论，对于超千米深立井井筒的设计有一些局限性[19，20]。

根据“井壁与围岩相互作用”理论分析可知，随着井筒的施工，井筒围岩经历了从三维受力状态到二维受力状态的改变，相应的也将发生“荷载卸压→应力集中→围岩变形→围压稳定”的自适应过程。当井筒及时砌筑后，井壁与围岩间将产生耦合作用力，形成相互作用机制，两者间有了应力的传递和位移的协同[18-20]。作为承载结构之一的围岩，在拉麦公式中并没有得到体现，仅单独考虑井壁强度和井壁荷载，没有考虑井壁与围岩的“相互作用，共同承载”的特性。另外，在普通法施工中，基岩段井壁设计也没有考虑岩层含水渗透压对井壁的作用。

3 井壁与围岩共同承载理论

3.1 井壁与围岩共同承载理论力学体系

在井下工程体系中，井壁与围岩形成了一个有机整体，相互影响、相互作用。井壁与围岩共同承载理论的基础是系统地将两者之间的应力—应变关系纳入统一力学模型，引入水土耦合作用，考虑岩层含水渗透压的作用，建立井壁与围岩共同作用力学体系，并假设如下条件：

1)地层可理想化为各岩层的叠加，水平岩层井筒各项受力相等且对称，倾斜地层或不均衡应力场岩层按不均匀系数计算。

2)井筒开挖后，井壁及时浇筑，井壁与围岩形成了紧密弹性接触，可按小变形平面应变弹性力学模型解析两者的相互间作用。远离井筒处围岩应力场为原岩应力状态，可初步认为是弹性自重应力场。

3)井壁结构是指开挖后围岩经历弹性卸载后的及时支护结构，且围岩变形范围从内向外逐渐变小，当模型外部边界取足够大时，围岩位移将接近零。

4)考虑超千米深井井筒井壁短掘短砌施工以及岩体自承能力产生的应变效应作用，井筒水平应力可按平面应变效应计算。随着井壁及围岩蠕变的发生，由于处于自重应力场，两者垂直应力将趋于自重应力效应，按自重应力考虑。

5)假设太沙基有效应力原理在孔隙型含水基岩结构中仍适用，即静水压力和有效应力之和为总应力。围岩变形主要由有效应力作用产生，围岩应力场与渗流场没有相互影响，静力平衡方程中不考虑渗透力和水场力作用，认为地层变形主要由有效应力引起。暂不考虑围岩应力场与渗流场的耦合作用，围岩中水渗流符合达西定律，渗透系数为常数。

6)认为井壁主要起到承载围岩有效应力和外缘渗流压力，不考虑水体渗流导致的井壁混凝土材料的性质变化和围岩与井壁应力变化。

3.2 井壁与围岩共同承载理论力学模型

井壁与围岩共同承载支护体系中，采用厚壁筒理论，同时将井壁与围岩的应力-应变关系纳入同一模型，并引入了水土耦合作用。

根据弹性力学中厚壁圆筒力学解析结果可知，井壁与围岩内部各点环向应力与径向应力。将解析式代入井壁与围岩共同承载力学模型中，可得距井筒中心距离为r处的围岩水平应力及径向位移为：

距井筒中心距离为r处的井壁水平应力及径向位移为：

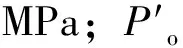
当r=r0时，井壁外缘处位移量等于围岩内缘位移量，即u=uco，将式(4)和式(7)联立可得：

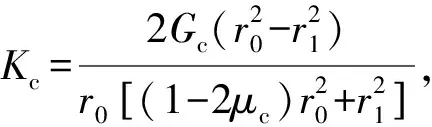
将式(9)经过重新解析，可得出井壁所受有效应力：

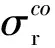
径向应力：

环向应力：

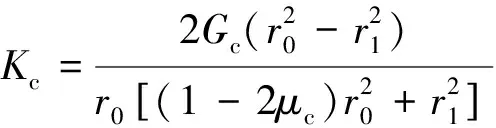
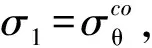
将式(13)代换简化可得：

设r0=r1+t，t为井壁厚度。

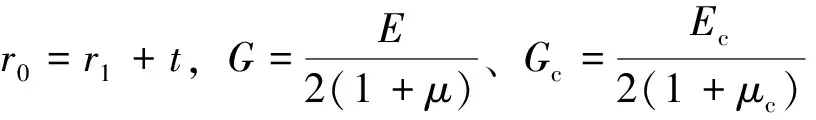
通过简化式(15)，得到井壁与围岩共同承载理论井壁厚度计算表达式：

式中，A、B均为与混凝土、围岩材料相关的材料系数；[σ]为混凝土井壁抗压强度，MPa。

4 工程设计应用及效果

4.1 井壁设计

以磁西一号矿井副立井井筒为例，取埋深1280 m泥岩段(隔水层)井壁和埋深1200 m砂岩段(含水层)井壁进行井壁荷载计算和井壁厚度设计，其中，砂岩含水层水头按1200 m计算，见表1和表2。

表1 副井井筒千米以下分层涌水量预计

表2 副立井井壁设计载荷计算

围岩及井壁有效应力侧压系数按式(19)计算；

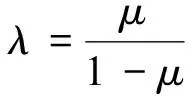
式中，λ、λc分别为围岩和井壁有效应力侧压系数，μ、μc分别为围岩和井壁泊松比。

设计井壁结构安全系数取1.35，选用C60混凝土，配筋率0.5%，按0.9折减系数计算钢筋混凝土抗压强度为26.1MPa，围岩及井壁材料物理力学参数见表3。

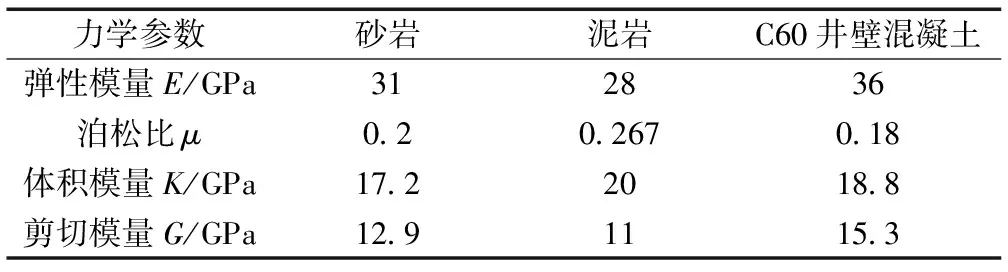
表3 围岩及井壁材料参数

将上述表1、表2、表3各参数代入井壁与围岩共同承载计算式(16)可得，埋深1280 m泥岩段(隔水层)井壁厚度为0.852 m，设计取0.9 m；埋深1200 m细砂岩段(含水层)井壁厚度为0.747 m，设计取0.8 m。

4.2 井壁施工方案及效果

副立井按净直径8.0 m，深度1341.6 m(含井底水窝)施工。井筒的表土及基岩风化段采用冻结法施工，冻结段深度245 m，采用双层钢筋混凝土井壁，外壁为500～600 mm，内壁为600～800 mm。井筒基岩段采用地面预注浆法施工，其中深度245～1100 m采用素混凝土井壁，厚600～800 mm；深度1100～1200 m采用钢筋混凝土井壁，厚800 mm；深度1200～1340 m采用钢筋混凝土井壁，厚度900 mm。磁西副井井筒(含马头门)2011年7月28日开工，2013年11月1日施工完毕，成井深度1341.6 m，实测井筒剩余水量4.88 m3/h左右。井筒至今使用完好。

5 结 论

1)为了克服传统井壁设计理论在千米深井井壁设计中存在的局限性，本文将井壁与围岩视为一个有机整体，并引入水土耦合作用机理，提出了井壁与围岩共同承载理论，系统地将两者之间的应力-应变关系纳入数字化体系中进行定量化计算。

2)在井壁与围岩共同承载支护体系中，井壁厚度与井壁混凝土、围岩性质、有效应力和水压相关，且相互影响、相互作用。

3)通过应用井壁与围岩共同承载表达式，得到了磁西一号矿井副立井(深1341.6 m)井壁合理厚度和支护结构，井筒施工完毕后安全、完好，结果表明井壁与围岩共同承载理论及表达式符合千米深井井壁设计要求。