平面P波入射软弱结构面传播特征研究
2023-09-25李春鹏,李远远,仝霄金
李 春 鹏,李 远 远,仝 霄 金
(济南市勘察测绘研究院,山东 济南 250101)
0 引 言
天然岩体往往存在各种软弱结构面,这些结构面内部被黏土、岩屑、岩块等填充。由于充填介质与两侧岩体物理力学性质相差较大,导致结构面容易产生失稳破坏,尤其在动载作用下,当由地震或工程爆破产生的应力波到达软弱结构面时会发生透反射,这一过程中应力波引起的动态响应可能会引发结构面滑移、错动、倾覆等,对工程以及周边场地造成不利的影响。
国内外学者对应力波入射无充填节理的传播规律开展了大量研究工作。Nolte[1]、Myer[2]、Schoenberg[3]等基于位移不连续理论,研究了应力波入射结构面的透反射特性,分析了入射角、节理刚度、节理数量与厚度等对应力波传播规律的影响;Zhao等[4]通过开展非线性变形不连续模型,研究了P波垂直入射单一节理的传播特性;柴少波等[5]基于时域递归法,分析了P波入射交叉节理的传播规律;卢文波[6]对应力波作用于滑移结构面的特征进行研究,揭示了滑移结构面的高频滤波作用;刘啸等[7]基于应力波入射结构面的透反射关系,建立了结构面剪切滑移失稳力学模型。
对于软弱结构面,由于充填介质的影响使得应力波传播更加复杂,部分学者开展了相关研究。李夕兵[8]考虑软弱结构面摩擦滑移边界条件,得到了软弱结构面对应力波传播的影响特征;Li[9]、刘婷婷[10]等基于三单元模型,采用特征线法得到了P波在软弱结构面处的传播规律,并讨论了充填介质、接触刚度等的影响特征;范留明等[11]采用射线理论分析了P波入射软弱夹层的传播特性,从能量角度探讨了波阻比等因素的影响;贾帅龙等[12]基于时域递归法研究了充填节理对应力波传播规律的影响,分析了充填节理法向与切向力学性质的变化规律。
此外,一些学者基于室内试验开展了软弱结构面相关研究。刘汉香等[13]通过开展振动台试验研究了含软弱夹层边坡的地震响应特征;周飞等[14]基于模型试验分析了含水平软弱夹层边坡的动力响应特性;Wu[15]等采用SHPB试验探讨了含水率对P波在充填结构面岩体中衰减规律的影响。随着计算机技术的发展,在数值模拟方面也有一些研究。廖少波等[16]采用3DEC研究了结构面产状对岩质边坡动力响应的影响;胡建华等[17]采用LS-DYNA分析了充填结构面对于爆炸应力波传播的影响特征;Chen等[18]基于颗粒离散元法,研究了地震波在含软弱夹层岩质边坡中的传播特征,进行了边坡稳定性分析。
综上所述,对于软弱结构面应力波传播特征问题,国内外学者大多采用理论分析方法开展相关研究,明确了应力波穿过软弱结构面的透反射特性,但大部分研究并未考虑上下岩体与软弱夹层的接触关系,仅仅考虑了单个接触面边界条件的影响。因此,本文基于软弱结构面理论模型,采用应力波理论对P波入射软弱结构面传播特征进行分析,并采用FEM数值模拟方法验证理论结果的正确性,分别讨论P波入射角、频率、结构面剪切参数、充填材料力学参数以及充填厚度等因素对应力波传播的影响特征,对比研究软弱结构面滑移前后应力波透反射特性,为含软弱结构面地质构造场地稳定性控制提供理论参考。
1 平面P波理论分析
1.1 软弱结构面理论模型
天然岩体中存在大量软弱结构面,填充材料不同于岩体,往往是容易受到剪切破坏的砂砾、黏土等。由地震或者工程爆破在岩体中产生的应力波主要为P波和SV波,应力波从一侧入射结构面时,会分别在结构面两侧发生透射与反射。由于P波易使岩体产生拉伸破坏,在研究软弱结构面动力特性时优先考虑P波入射情况。基于此过程,建立由厚度为h的软弱夹层以及无限岩体组成的软弱结构面理论模型,如图1所示,各组分均假定为线弹性、均匀、各项同性介质。
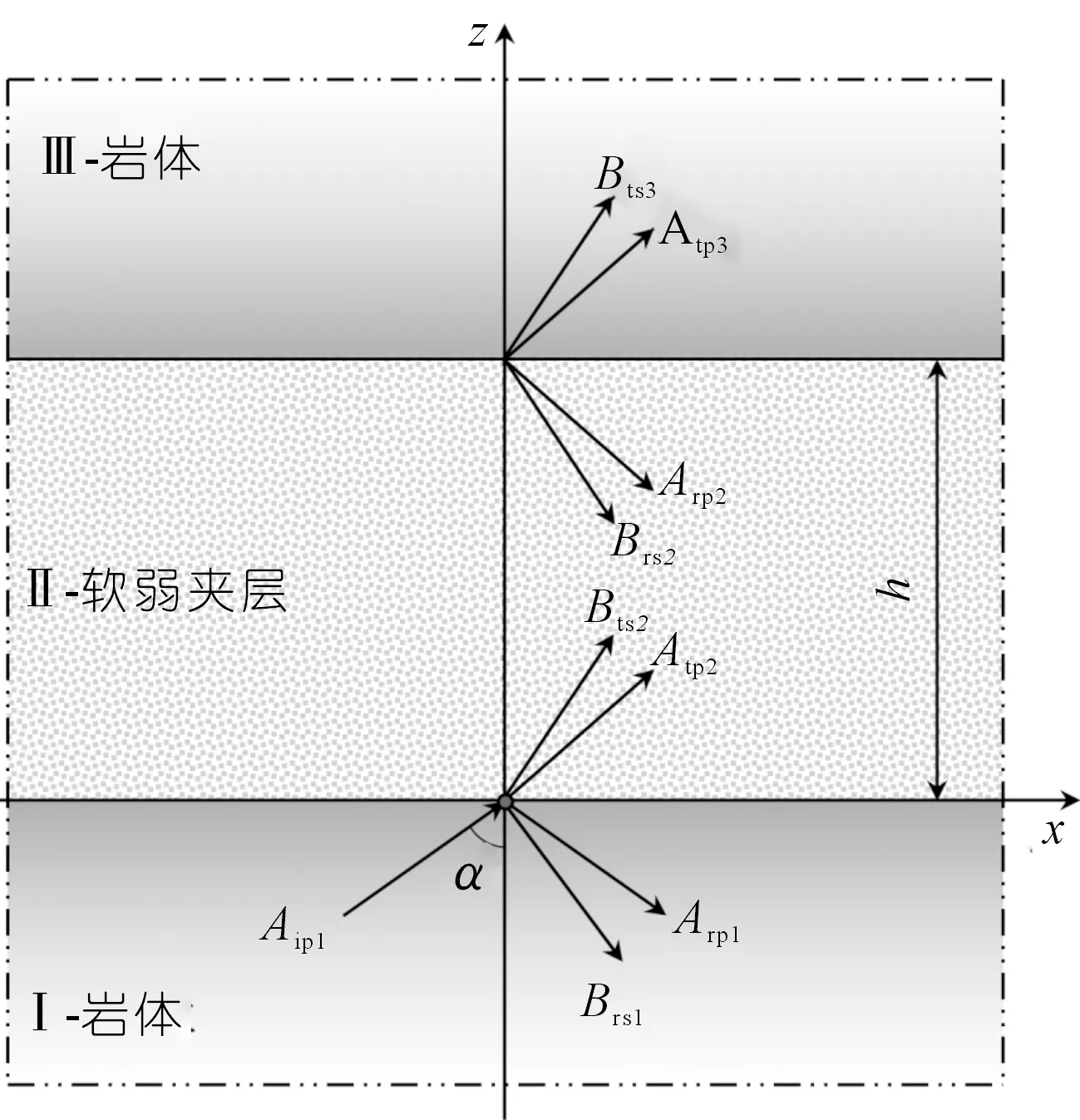
图1 软弱结构面理论模型Fig.1 Theoretical model of weak filled structural plane
1.2 P波入射软弱结构面的透反射关系
设有一均匀平面简谐P波从一侧岩体(Ⅰ-岩体)入射软弱结构面,入射角为α。在穿过结构面时会产生反射波和透射波,如图1所示,其中在z<0区域内(I-岩体)存在入射P波、反射P波和反射SV波,振幅分别为Aip1、Arp1、Brs1;在0
在Ⅰ-岩体中应力波的位移势函数可表示为
(1)
在Ⅱ-软弱夹层中应力波的位移势函数可表示为
(2)
在Ⅲ-岩体中应力波的位移势函数可表示为
(3)
式中:φ(n)、ψ(n)分别为第n层介质P波、SV波位移势函数(n=1,2,3);ω为应力波圆频率;i为虚数单位;t为传播时间;kwx、kwz分别为应力波在x和z方向的波矢量,w表示波型,沿传播路径的波矢量kw表示为
(4)
式中:cp、cs为介质P波波速与S波波速,对于各向同性弹性介质,可通过公式(5)计算得到
(5)
式中:λ为介质拉梅常数,μ为介质剪切模量,代入理论模型中的介质参数可得到相应波速。
根据Snell定理,各应力波在x方向的波矢量相等,即
kip1x=kip1sinα=krp1x=krs1x=ktp2x=kts2x
=krp2x=krs2x=ktp3x=kts3x=kx
(6)
对于同一介质中相同类型的应力波,波数是一致的,即
(7)
确定了位移势函数形式后,需要结合边界条件求解各应力波大小。由于软弱结构面填充介质与两侧岩体性质相差较大,在接触面上容易发生剪切滑移,这种剪切滑移行为一般采用摩尔-库伦强度准则进行描述。基于此特点,可以将应力波入射软弱结构面的动力作用过程分为结构面未滑移、结构面滑移两个阶段。对于结构面未滑移阶段,软弱夹层与岩体接触面相互粘结,接触面两侧介质位移与应力均满足连续条件,即
(8)
(9)
对于结构面滑移阶段,考虑两侧接触面均发生滑移的情况,假定结构面未发生张裂,则接触面两侧切向应力和切向位移不连续,且切向应力符合摩尔-库伦准则,设结构面黏聚力为c、内摩擦角为θ,则有
(10)
(11)
上式中θe为等效内摩擦角,满足以下关系[7]:
σzztanθe=σzztanθ+c
(12)
采用Helmholtz分解定理,可将基岩位移场u分解为矢量场φ与标量场ψ:
u=∇φ+∇×ψ
(13)
式(13)展开为x与z方向,得到
(14)
理论模型中各组分均假定为各向同性弹性介质,其应力应变关系应满足线弹性胡克定律,应力由位移势函数形式表示为
(15)
将式(1)~(3)代入式(13)、(14)中得到应力场、位移场,联立式(8)~(11),结合式(4)~(7)条件得到振幅方程式。对于结构面未滑移的,有
(16)
对于结构面滑移的,有
(17)
矩阵中各分量见附录。应力波的透反射关系一般采用透反射系数表示,即透反射波振幅与入射波振幅比值。定义该比值为Z,各应力波透反射系数可表示为
(18)
2 基于有限元数值模拟的理论验证
2.1 数值建模及参数
应力波理论解析的正确性可通过相似研究和数值方法进行验证,在本文中采用有限元数值模拟进行对比验证。ANSYS/LS-DYNA是一款显式动力有限元软件,适用于进行动力分析,因此用于本文模型验证是可靠的。图1中两侧岩体均为半无限岩体,结构面也具有延展性,这种无限边界在数值模型中可通过设置透射边界来实现,因此模型大小只要满足计算要求即可。根据图1理论模型概况,建立整体尺寸为4 m×4 m 的二维有限元模型,其中软弱夹层厚度为5 cm,倾斜角度为10°,两侧岩体平均高度为197.5 cm。模型采用4节点Solid162实体单元,同时应用Lagrange网格进行划分。为了更为准确地反映应力波的传播,单元网格尺寸控制在应力波波长的1/6~1/12,本文选取网格尺寸为波长的1/10,考虑到软弱夹层厚度较小,在划分网格时适当减小尺寸,数值模型如图2所示。

图2 FEM数值模型(尺寸单位:m)Fig.2 FEM numerical model
由于理论模型中各组分均为线弹性,因此在数值模型中岩体与软弱夹层均设置为线弹性材料(*Mat_Elastic),具体参数如表1所列。

表1 数值模型材料参数Tab.1 Material parameters of numerical model
在1.2节中计算了粘结边界条件和滑移边界条件两种动力形式解,因此在数值模型中需要考虑两种不同的边界条件。如图3所示,粘结边界条件通过共节点方式实现,该方法要求接触面两侧共用同一节点,满足应力与位移连续,而滑移边界条件通过添加接触方式实现,在LS-DYNA中提供了摩尔-库伦接触方式。本文模型采用二维自动面-面接触,设置等效摩擦角θe为10°。
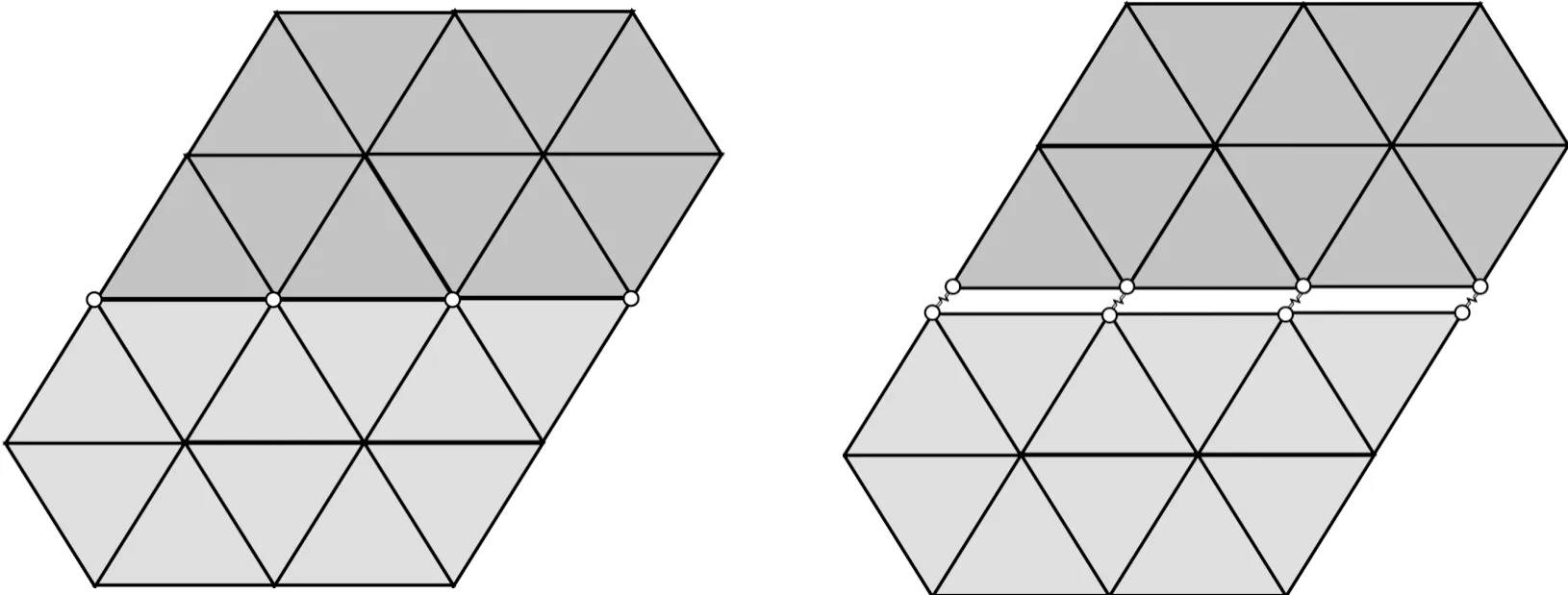
图3 粘结接触(左)与滑移接触(右)示意Fig.3 Schematic diagram of bonding contact (left) and sliding contact (right)
考虑简单垂直入射情况,将输入荷载加载于Ⅱ-软弱结构面下边界处。假定输入位移是振幅为0.01 cm、频率为200π的正弦波,只考虑一个周期,即0 ≤T≤0.01 s,表达式为
(19)
由数值模型可知软弱结构面与初始波阵面的距离与角度相关,假定初始波阵面距离结构面L,应力波经过t0=L/crp入射结构面,此时应力波位移函数为
(20)
2.2 数值模拟结果与理论对比分析
为了便于对比数值模拟与理论解析结果,定义同一水平位置下Ⅰ-岩体处接触面位移峰值u0与Ⅱ-岩体处接触面位移峰值ui之比为D,可表示为
(21)
将式(1)代入式(14)中得到Ⅰ-岩体处位移
(22)
将式(3)代入式(14)中得到Ⅲ-岩体处位移表达式为
(23)
联立式(20)~(23),结合透反射系数可得到水平位移比Dx与垂直位移比Dz。选取数值模拟中相同水平位置下位移比D,得到粘结界面与滑移界面情况数值模拟与理论解析位移比如图4所示。对于两种接触条件下,有限元数值模拟结果均与理论结果相近,误差在允许范围,表明应力波理论解析是准确可靠的,可用于后续分析。此外,对比滑移界面与粘结界面可知,结构面在粘结状态下水平位移比约为垂直位移比的1.2倍,而结构面在滑移状态下水平位移比约为垂直位移比的3.4倍,表明滑移失稳下上盘岩体水平位移过大,容易沿结构面向下运动造成滑坡等灾害,因此需进一步明确P波入射软弱结构面的传播特征。
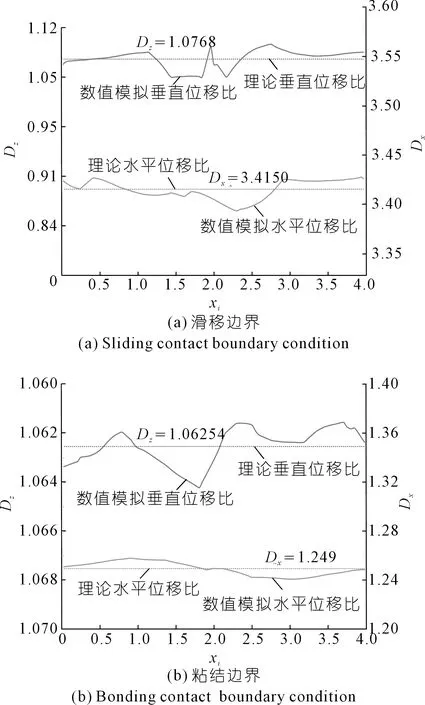
图4 不同接触条件下理论与数值模拟位移比DFig.4 Theoretical and numerical simulation D under different contact conditions
3 参数分析与讨论
以2.1节中材料参数为基本物理参数,展开对平面P波入射软弱结构面传播特征研究。
3.1 P波入射角的影响
在地震或工程爆破过程中应力波从震源发出,波阵面到达结构面时往往存在多个入射角。根据第1节应力波理论分析可知,不同入射角下P波透反射系数不同,因此在0°~90°范围内均匀选取10个入射角,得到粘结边界与滑移边界条件透反射系数随入射角变化关系如图5所示。从图中可以看到,当不同入射角P波入射结构面时,结构面在粘结状态和滑移状态下随入射角呈现相似的变化趋势,但从整体上看滑移状态下透反射系数偏小,这是由于结构面滑动摩擦产生损耗导致的。当P波入射角为60°时,反射SV波达到峰值,但其余透反射波均为0,表明此时P波入射下只在Ⅰ-岩体中产生反射SV波,这种反射波应当为不均匀波。
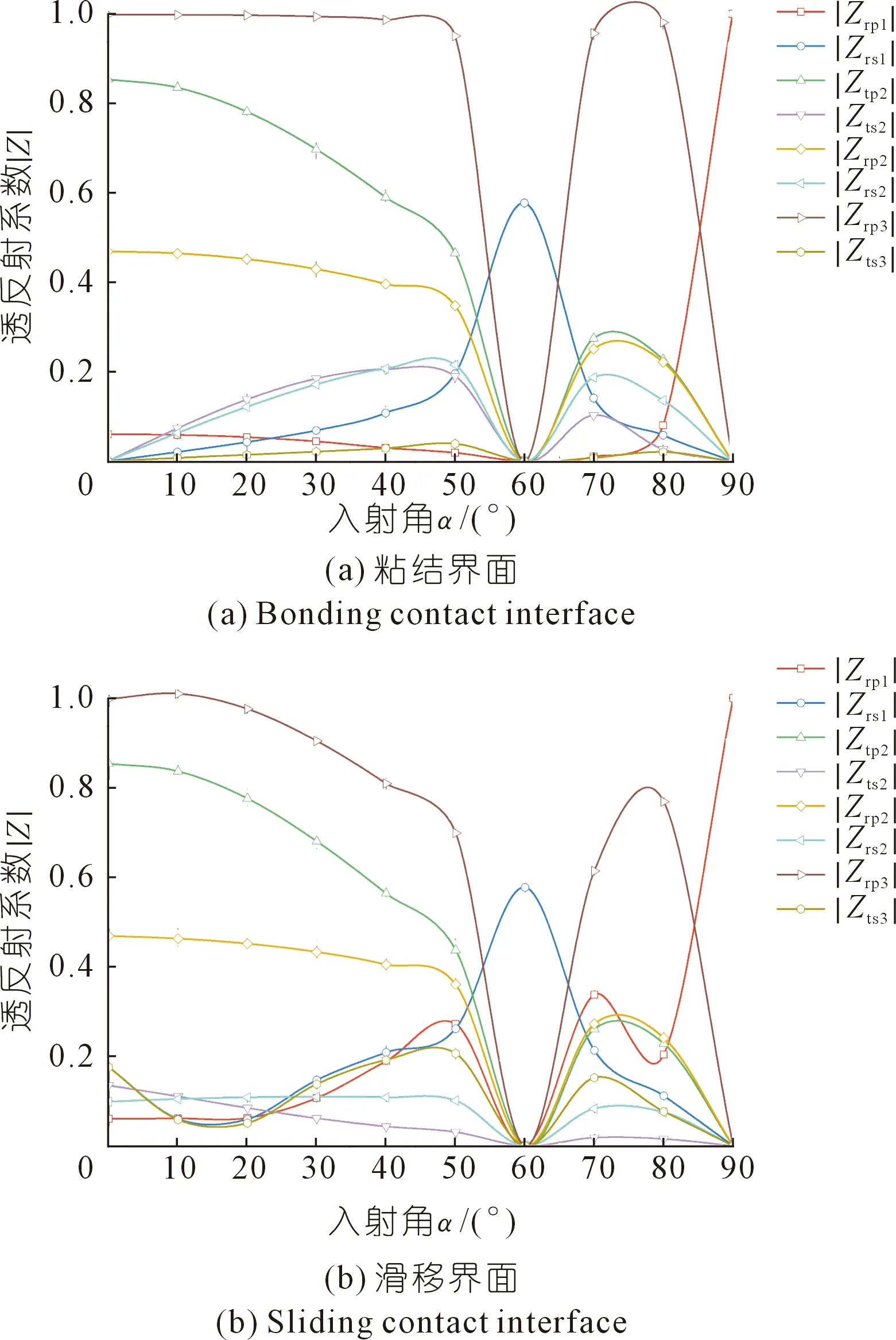
图5 不同入射角透反射系数Fig.5 Transmittance and reflection coefficient at different incident angles
对于处于粘结状态的结构面,在入射角为0~60°之间,Ⅰ-岩体中反射P波一直处于较小值且呈减小趋势,而反射SV波呈现快速增大趋势,表明反射能量基本转化为SV波,结构面处于剪切状态;Ⅱ-软弱夹层中,透射P波和反射P波呈现持续减小的趋势,透射SV波和反射SV波呈现先增大后减小的趋势,在50°~60°之间均表现为迅速衰减,表明在该角度范围内软弱夹层剪切作用逐渐显著;Ⅲ-岩体中,透射SV波系数一直处于较小值,而透射P波在0°~50°之间一直保持为1,表明软弱充填结构面并未对P波起到削弱作用。在入射角为60°~90°之间,Ⅰ-岩体中反射P波逐渐增大,在入射角为80°时开始迅速增长至1,反射SV波则逐渐减小至0,这与入射角为0~60°时完全相反;在Ⅱ-软弱夹层与Ⅲ-岩体中,各透反射波均表现为先增大后减小的趋势,并均在70°~80°之间达到峰值。因此,处于粘结状态的软弱结构面在P波入射角较大时受到扰动更小,尤其在入射角为50°~70°之间时。
对于处于滑移状态下的结构面,相比于粘结状态,Ⅰ-岩体中反射P波与Ⅲ-岩体中透射P波以及透射SV波表现较为不同。其中,Ⅰ-岩体中的反射P波随入射角增大呈现波动趋势,其反射系数远大于粘结状态,表明在滑移状态下反射波能量显著增长,而Ⅱ-软弱夹层中透射SV波普遍较小,也证明结构面滑移会影响透反射能量分配。Ⅲ-岩体中透射P波在入射角为0°~50°之间并未保持恒定,而是呈现衰减趋势,同样在入射角为70°~80°之间透射系数仍未达到1,在这一传播过程中P波能量部分提供给结构面滑动做功。此外,Ⅲ-岩体中透射SV波随入射角变化呈现波动趋势,相比粘结状态具有较大的透射系数,表明滑移状态下结构面剪切作用增强。综合两种状态来看,当软弱充填结构面从粘结状态进入滑移状态时,结构面整体响应会降低,但剪切作用增强。
3.2 入射P波频率的影响
当软弱结构面离震源较近时,入射P波频率较大,当软弱结构面离震源较远时,入射P波频率较小,根据以往研究可知软弱介质往往具有高频滤波作用,因此需要讨论软弱结构面对频率的敏感程度。选取入射波频率(f)分别为10,100,1 000,10 000 Hz,其余参数保持不变。根据图5结果,在Ⅲ-岩体中的透射P波在不同入射角下均保持较大值,因此着重分析应力波穿过结构面后透射P波的透射系数。不同入射波频率下|Ztp3|随入射角的变化趋势如图6所示。

图6 不同频率下|Ztp3|随入射角变化趋势Fig.6 Variation trend of |Ztp3| with incident angle at different frequencies
从图6中可以看到,不同频率入射P波作用下,粘结状态和滑移状态软弱充填结构面表现为相同的变化趋势。随着频率的增大,同一入射角下|Ztp3|呈现减小趋势,其中当入射波频率处于中低频时,同一入射角下|Ztp3|未有太大衰减,当入射波频率处于高频时,同一入射角下|Ztp3|产生较大衰减,这充分体现了软弱充填介质的高频滤波特性。因此,当软弱充填结构面离震源或爆源较远时也可能发生失稳,当软弱充填结构面离震源或爆源较近时将产生直接破坏。
3.3 结构面剪切参数的影响
在结构面的剪切滑移影响下,两侧岩体在水平向发生相对滑动,不同的剪切参数必然导致相对滑移的位移不同。从3.1节分析可知,结构面为滑移和粘结状态下,透反射系数在入射角较大和较小时有差别,说明在不同接触条件下应力波耗散程度不同,为了明确结构面剪切参数对应力波传播的影响,计算等效摩擦角为0°,5°,10°,15°,20°时的透反射系数,如图7所示。从图7(a)中可知,同一P波入射角下,随着等效摩擦角的增大,P波反射系数逐渐减小,而透射系数逐渐增大,但 Ⅱ-软弱夹层中的P波透反射系数对等效摩擦角不敏感。从图7(b)中可知,等效摩擦角为0°时S波透反射关系不同,与其他等效摩擦角最大的区别在于当P波入射角为0°时,SV波透反射系数均为0,从整体来看,随着等效摩擦角增大,岩体中SV波系数逐渐减小,而软弱夹层中SV波系数逐渐增大,这是软弱夹层易发生剪切破坏的原因。综合P波和S波透反射系数可知,随着等效摩擦角增大,穿过软弱结构面透射P波能量增大,透射S波能量减小,表明剪切变形越难发生。
3.4 充填材料力学参数的影响
充填材料的力学性质会影响应力波的透反射系数,特别是应力波穿过界面两侧介质的波阻抗,对应力波的传播衰减影响较大。在结构面两侧岩体参数不变的情况下,考虑将充填材料波阻抗作为变量研究应力波的透反射关系。由于波阻抗存在密度和波速两个变量,因此固定密度保持不变,只改变波速。为了更好描述材料力学参数的影响,定义充填材料波阻抗与岩体波阻抗之比为γ,可知在第3节材料参数下γ为0.291,在0.05~0.5之间均匀选取10个值,得到入射角为30°时不同γ影响下结构面的透反射系数的变化规律如图8所示。

图8 不同波阻抗比γ下透反射系数随入射角变化趋势Fig.8 Variation trend of transmittance and reflection coefficient with incident angle for different γ
从图8(a)中可知,结构面透反射系数在粘结状态下随着波阻抗比γ逐渐增大,Ⅰ-岩体中反射波逐渐减小并趋于0;Ⅱ-软弱夹层中透射P波逐渐增大,在γ>0.1后增长趋势较缓且恒定,反射P波先增大后减小,在γ>0.1 后减小趋势较缓且恒定,而反射SV波与透射SV波均随γ增长并在γ>0.2后保持恒定;Ⅲ-岩体中透射P波在0<γ<0.25时迅速增大,而后维持在1.0保持不变,透射SV波表现为先增大后减小,在γ>0.1时逐渐减小并趋于0。由此可见,当P波穿过结构面引起的振动受γ控制,当γ>0.25后软弱充填结构面无法起到削弱应力波的作用。
从图8(b)中可知,结构面在滑移状态下表现出和粘结状态相似的变化趋势,不同之处在于穿过结构面后的透射P波对γ更不敏感,即当γ>0.2后,透射系数保持在1.0附近,并且稍大于1.0,表明在滑移状态下高波阻抗比将对入射P波起到放大作用。
3.5 充填厚度的影响
应力波在含软弱充填结构面处传播时,充填介质厚度是不可忽视的。不同充填介质厚度使得应力波传播路径不同,由此导致的透反射特性也不同。为了充分考虑充填介质的厚度,在10~100 mm范围内均匀选取10个充填厚度,分析粘结界面与滑移界面的透反射特性。入射波参数、介质参数与接触参数见第3.0节,其中固定入射角为30°,得到不同充填厚度下透反射系数如图9所示。

图9 不同充填厚度下透反射系数随入射角变化趋势Fig.9 Variation trend of transmittance and reflection coefficient with incident angle for different filling thicknesses
从图中可以看到粘结状态和滑移状态下结构面透反射系数随着充填厚度的增加呈现波动变化,其中Ⅰ-岩体中反射P波和反射SV波波动趋势与其余波正好相反。重点关注穿过结构面后的透射P波。从图9中可以看到,当充填厚度在0.04,0.08 m时,透射系数都达最大值,对于粘结状态下透射系数峰值相对一致,而滑移状态下透射系数峰值相对降低。可见随着充填厚度增加,透反射系数呈现周期变化,每隔0.04 m透射系数达到峰值,滑移状态下透射系数呈减小趋势。
4 结 论
本文通过应力波理论求解得到平面P波入射软弱结构面时粘结状态与滑移状态下的透反射关系,并采用LS-DYNA模拟验证了理论的正确性,最后分析了入射角、频率、结构面剪切参数、充填材料性质与厚度等对P波传播的影响特征,得到结论如下:
(1) 不同入射角下粘结状态与滑移状态下应力波传播特征相近,但滑移状态下应力波透反射系数稍低,这是由于滑移过程中存在能量损耗,此外入射角为60°时只存在反射S波,在该角度下只存在剪切破坏。
(2) 软弱充填结构面具有高频滤波特性,表明即使在低频下,软弱充填结构面也容易发生破坏,而高频下产生的破坏更多是在入射波处岩体,因此对于工程爆破软弱结构面起到削弱作用,导致结构面上盘容易产生大块岩体,对于地震作用下需要时刻关注结构面两侧的稳定性。
(3) 等效摩擦角可控制软弱结构面的剪切滑移,当等效摩擦角增大时,穿过软弱结构面透射P波能量会随之增大,而透射SV波能量减小,表明剪切变形越难发生。
(4) P波穿过软弱结构面振幅受充填介质与岩体波阻抗比控制,粘结状态下波阻抗比大于0.25时,透射系数基本保持恒定,滑移状态下波阻抗比大于0.2时基本保持恒定。
(5) 随着软弱结构面厚度增大,应力波幅值呈现周期波动式变化,周期为0.04 m,该现象可能与入射P波波长相关,需要进一步研究。
(6) 岩土工程中应根据震源与软弱结构面分布确定潜在滑移位置,在抗震方面需注重软弱结构面的加固,在工程爆破方面需充分利用软弱结构面选择合理的爆破位置达到破岩、减振等效果。
附录:
矩阵[a]中分量aij表达式为
a17=a18=0,a21=-2krp1zkxμr,
a31=-krp1z,a32=-a34=-a36=-kx,
a33=-ktp2z,a35=krp2z,a37=a38=0,
a41=-a43=-a45=-kx,a42=krs1z,a44=kts2z,
a46=-krs2z,a47=a48=0,a51=a52=0,
a54=-2eih(ktp2z+ktp3z+kts3z)kts2zkxμs,
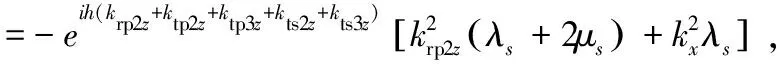
a56=2eih(krs2z+ktp2z+ktp3z+kts2z+kts3z)krs2zkxμs,
a58=2eih(ktp2z+ktp3z+kts2z)kts3zkxμr,a61=a62=0,
a63=-2eih(ktp3z+kts2z+kts3z)ktp2zkxμs,
a65=2eih(krp2z+ktp2z+ktp3z+kts2z+kts3z)krp2zkxμs,
a67=2eih(ktp2z+kts2z+kts3z)ktp3zkxμr,
a71=a72=0,a73=-eih(ktp3z+kts2z+kts3z)ktp2z,
a74=eih(ktp2z+ktp3z+kts3z)kx,
a75=eih(krp2z+ktp2z+ktp3z+kts2z+kts3z)krp2z,
a76=eih(krs2z+ktp2z+ktp3z+kts2z+kts3z)kx,
a77=eih(ktp2z+kts2z+kts3z)ktp3z,
a78=-eih(ktp2z+ktp3z+kts2z)kx,a81=a82=0,
a83=-eih(ktp3z+kts2z+kts3z)kx,
a84=-eih(ktp2z+ktp3z+kts3z)kts2z,
a85=-eih(krp2z+ktp2z+ktp3z+kts2z+kts3z)kx,
a86=eih(krs2z+ktp2z+ktp3z+kts2z+kts3z)krs2z,
a87=eih(ktp2z+kts2z+kts3z)kx,a88=eih(ktp2z+ktp3z+kts2z)kts3z
矩阵[b]中分量bij表达式为
b31=-kip1z,b41=kx,b51=b61=b71=b81=0
矩阵[c]中分量cij表达式为
c87=eihkts3z{-2ktp3zkxμr
c43=c44=c45=c46=c47=c48=c81
=c82=c83=c84=c85=c86=0,
其余项与矩阵[a]对应项一致。
矩阵[d]中分量dij表达式为
其余项与矩阵[b]对应项一致。
