融合海温偶极因子的长期月径流预报研究

刘建华，徐文馨，石昕颜，陈 杰，胡召根，陈 华

（1. 天生桥一级水电开发有限责任公司水力发电厂，广东 广州 510600； 2. 水资源与水电工程科学国家重点实验室 武汉大学，湖北 武汉 430072； 3. 海绵城市建设水系统科学湖北省重点实验室（武汉大学），湖北 武汉 430072）

0 引 言

径流预报中通常将预见期在一个月以上、一年以内的预报称为长期预报。有效的长期月径流预报对于水库的综合利用有着十分重要的意义，特别是对于以发电为主的水库来说，准确预报入库流量是编制年度以及各季度发电计划的重要基础［1，2］。

大部分水库都建在山区，气象水文条件复杂，雨量站和水文站建设条件较差，缺乏高质量水文气象实测资料，给长期径流预报模型的构建带来了较大的难度［3］，其中，气象资料不足是限制以水文模型为基础的过程驱动长期径流预报模型使用的重要原因。因此，数理统计方法，以多元线性回归为代表，因模型简单，实现方便，对数据变化的适应性高，可以在实际工作中有效地指导生产实践，应用最为广泛［4-7］。现有研究多在分析径流与前期多因子之间的统计相关关系后，通过构建变因子多元线性回归模型实现对不同预见期的径流预报。

一般而言，长期的水文动态需要考虑水文大循环，即水在陆地、海洋和大气3 种介质中的相互转化。河川径流的形成和季节性变化受到海温和大气环流因子的共同作用，故从水文循环的机理出发，综合分析影响区域水文情势的物理因素，是长期径流预报应遵循的基本原则［1］。近代的大气环流实测资料无论在种类还是时空尺度上都十分丰富，且获取方便，已被广泛用作长期径流预报因子［8，9］。海洋对大气变化具有独特的“记忆功能”和“低通滤波”作用，因此海洋表面温度场一直被认为是影响大气环流和引起气候异常的重要因素，其也已被引入预报模型指示径流变化规律［10-14］。然而现有研究多采取固定海域的海洋表面温度场［15-19］，包括厄尔尼诺活动区域和对我国水文情势影响明显的北太平洋地区格点海温数据，忽略了海域温度场分布对区域径流的影响。鉴于此，本研究将考虑海温场的“偶极型”空间分布特征，探究不同海域温度场的关联性对长期径流预报的指示价值。

研究以南盘江流域天生桥一级（天一）水库上游为研究对象，综合考虑水库前期径流、大气环流因子和海温偶极因子作为多元线性回归模型的关键因子，在年内各月分别构建预见期为1～12个月的径流预报模型，并探讨因子组合方式对预报效果的影响，以期为其他流域的长期月径流预报提供参考。

1 研究区域与数据

1.1 研究区概况

天生桥一级（天一）水库位于珠江流域西江水系上游的南盘江流域，其坝址以上集水面积为50 139 km2。南盘江流域属于亚热带季风气候区，干湿季节变化明显。5 月至10 月（夏半年）受西南季风影响，温和多雨，且降水集中；11 月至次年4 月（冬半年）受大陆气团影响，干暖少雨，常出现干季。天一水库为不完全多年调节水库，多年平均年径流量为193 亿m3，总库容为102.6 亿m3，以发电为主要任务，是国家“西电东送”的龙头水库，在“西部大开发”中起着重要作用。然而，流域缺乏可靠的长期历史气象数据，降雨资料缺、漏测时间长且质量不高，为天一水库构建预报精度满足电厂需求的长期径流预报模型面临着很大的挑战。天一水库上游流域如图1所示。

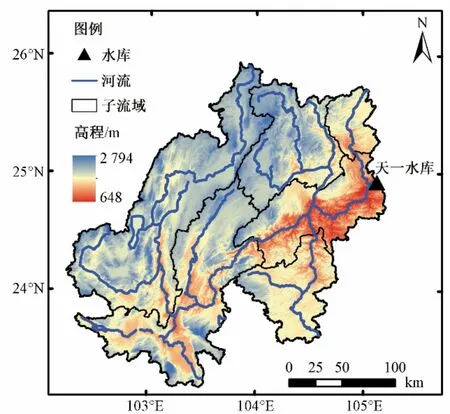
图1 天一水库流域图Fig.1 Location and characteristics of the Tianyi reservoir

1.2 研究数据

（1）月径流数据由天一电厂提供，选用时段为1953 年1 月至2020年12月。

（2）大气环流因子下载自中国气象局国家气候中心网站（https：//www.ncc-cma.net/），每月初更新上月实测数据。网站共提供88项大气环流指数，若指数缺测月数大于选用数据序列长度10%，则该指数弃用；其余有缺测项的指数，缺测项用其余部分均值插补，最终有75项大气环流指数被保留，如表1所示，用于后续模型构建，选用时段为1953年1月至2020年12月。

表1 选用的75项大气环流指数Tab.1 Information of selected 75 atmospheric indices.

（3）海温数据选用Kaplan Extended SST V2海温波动月值数据资料，下载自美国海洋与大气管理局网站（http：//www.esrl.noaa.gov/psd/），该数据集是目前公认的可靠性较高的海温数据集之一［20，21］，空间分辨率为5°×5°，选用的时间跨度为1953 年1 月至2020年12月。

2 研究方法

研究方法主要由①待选预报因子集生成；②预报因子筛选；和③多元线性回归模型构建3 部分组成，以下对3 部分作简要介绍。①由于大气环流和海温因子对径流的影响往往在几个月甚至更长的滞后时间之后才能反映出来，因此在长期径流预报中，需要考虑各因子对径流的影响滞后期。本研究对所有预见期均考虑预报发起点前推12个月的历史径流、大气环流和海温偶极作为待选预报因子，通过将不同的预报因子组合共生成7种待选预报因子集（即预报因子只考虑前期径流、只考虑大气环流、只考虑海温偶极、考虑径流和大气环流、考虑径流和海温偶极、考虑大气环流和海温偶极、考虑径流、大气环流和海温偶极）。②以待预报月径流为因变量，以各预报因子为自变量，通过对自变量与因变量的相关性进行显著性检验完成预报因子初选后，再通过逐步回归法进一步筛选预报因子。③多元线性回归模型构建过程中选用奇数年率定偶数年验证的方法，对年内各月各预见期分别构建7种因子组合的预报模型。下文对各部分作详细介绍。

2.1 海温偶极模型

研究表明，不同海域的表面海温场（SST）存在着一定的空间关联性，利用SST 的偶极特征构建的统计预报模型对降水和径流的指示作用甚至优于传统的ENSO 事件［22］。SAJI 等［23］研究发现海温场的空间分布具有偶极的特征，基于此，美国佐治亚理工学院的GEORGAKAKOS 教授团队［22］提出了一种海温偶极模型，通过在全球海域筛选与区域降水相关的海温场以构建偶极模型预报未来降水，其中，海温偶极的定义是特定大小和地理位置上两个海洋区域的平均表面温度异常的函数，表示成两个海区表面温度场的差或和。关于海温偶极的筛选和模型构建的详细过程可参考CHEN［22］和QIAN［24］等人的文章，以下就本研究对海温偶极模型的使用作简要说明。主要步骤为：①以Gerrity Skill Score（GSS）评分方法［25］为标准，从海温网格大数据中识别显著的海温偶极，将其配对、扩展、筛选后，得到海温偶极的最终形态；②重复步骤①后得到多对海温偶极，为年内各月分别挑选与径流序列相关性最为显著的海温偶极；③以所有显著海温偶极区域海温差为预报因子，以径流为预报对象，对年内各月分别构建线性回归模型，用留一交叉验证方法保留平均绝对误差最小的10个显著海温偶极区域海温差（即海温偶极因子）；④对预报发起点前推12 个月的海温场重复步骤①至③，获得12×10 个海温偶极，对每个影响滞时均保留10 个海温偶极因子中与奇数年实测径流序列皮尔逊相关系数最大的1个，作为长期径流预报模型的备选预报因子。

2.2 预报因子筛选

2.2.1 相关性分析

考虑到本研究的预报因子集可能过大，故先分别计算各因子和径流序列的皮尔逊相关系数，筛选出集合内与径流序列显著相关的因子。在本研究中，率定期（奇数年）年内各月样本数为33，显著性水平取0.05，则因子与径流序列相关系数大于0.344者通过相关性挑选。

2.2.2 逐步回归分析

经2.2.1 步骤筛选出的多个因子可能存在两两之间显著相关的情况，这会导致多元回归出现多重共线性的问题，从而影响预报效果，因此需要采用逐步回归法进一步筛选因子。逐步回归法是按自变量和因变量的显著性大小逐个引入变量，所以逐步回归会产生与引入步骤数量同样多的因子组合，对应多个多元线性回归模型。为得到因子数量合理、涵盖主要信息且率定期拟合效果合格的模型，在逐步回归分析中以率定期的修正复相关系数为标准确定回归的最终结果。修正的复相关系数矫正了复相关系数拟合优度对自由度的依赖关系，使得只有当自变量确实对因变量有所作用时值才会增加。在本研究中，率定期修正复相关系数达到0.8 时，对应的最少因子个数组合即为逐步回归最终结果；若所有因子组合在率定期拟合效果都无法达到修正复相关系数0.8，则选择达到0.75 对应的最少因子个数组合；达不到0.75 则选用0.65；率定期修正复相关系数小于0.65判定为无法有效拟合。

2.3 多元线性回归模型

多元回归模型能够比较全面地综合各个预报因子的作用。本研究将由逐步回归法挑选出的预报因子按最小二乘原理确定各因子的回归系数，建立多元线性回归方程，公式为：

式中：x（t）i为预报因子序列；i为预报因子序号；n为预报因子总个数；bc，i为回归系数；fc为常数项。

多元线性回归模型中的回归系数和常数项采用最小二乘法进行估计，最小二乘法的目标是使得预报结果与观测值之间的离差平方和最小，离差平方和的计算公式如下所示：

式中：m为样本数；j为样本点序号。

2.4 预报效果评价指标

长期径流预报的精度的计算公式参考《水文情报预报规范》（GB/T22482-2008）［26］，具体如下：

式中：Qoi和Qsi分别代表实测和预报月流量值。其中，预报值大于实际值2倍以上时，预报精度按0处理。

3 研究结果与讨论

图2展示了5月份预见期为6个月和9月份预见期为3个月时，筛选出的对天一水库入库径流影响最为显著的海温偶极，考虑文章篇幅问题，对其他月份各预见期对应的海温偶极筛选结果不一一展示。由图可知，5 月份6 个月预见期对应的正偶极子主要分布在太平洋和印度洋低纬度地区，负偶极子分布在东经40°至65°之间（印度洋）和东经180°（东太平洋）附近。9月份3 个月预见期对应的偶极在太平洋海域分布差别较大，没有明显的区域聚集规律。对于5 月份6 个月预见期而言，挑选出的偶极与Nino 34、Nino 4 海域有所重叠；对于9 月份3 个月预见期而言，北太平洋白令海峡附近海温异常现象重复出现，两种情况下对应的最显著的偶极均主要分布在印度洋海域内。由于海洋变化、大气环流及其交互作用十分复杂，不同海域的温度场之间的关联性和空间关系难以归纳出一般规律，我们较难对特定研究区域解释选取的正负偶极呈现的空间规律与关系的物理成因。本研究的重点不在此，但相关解释在未来的研究中应完善。

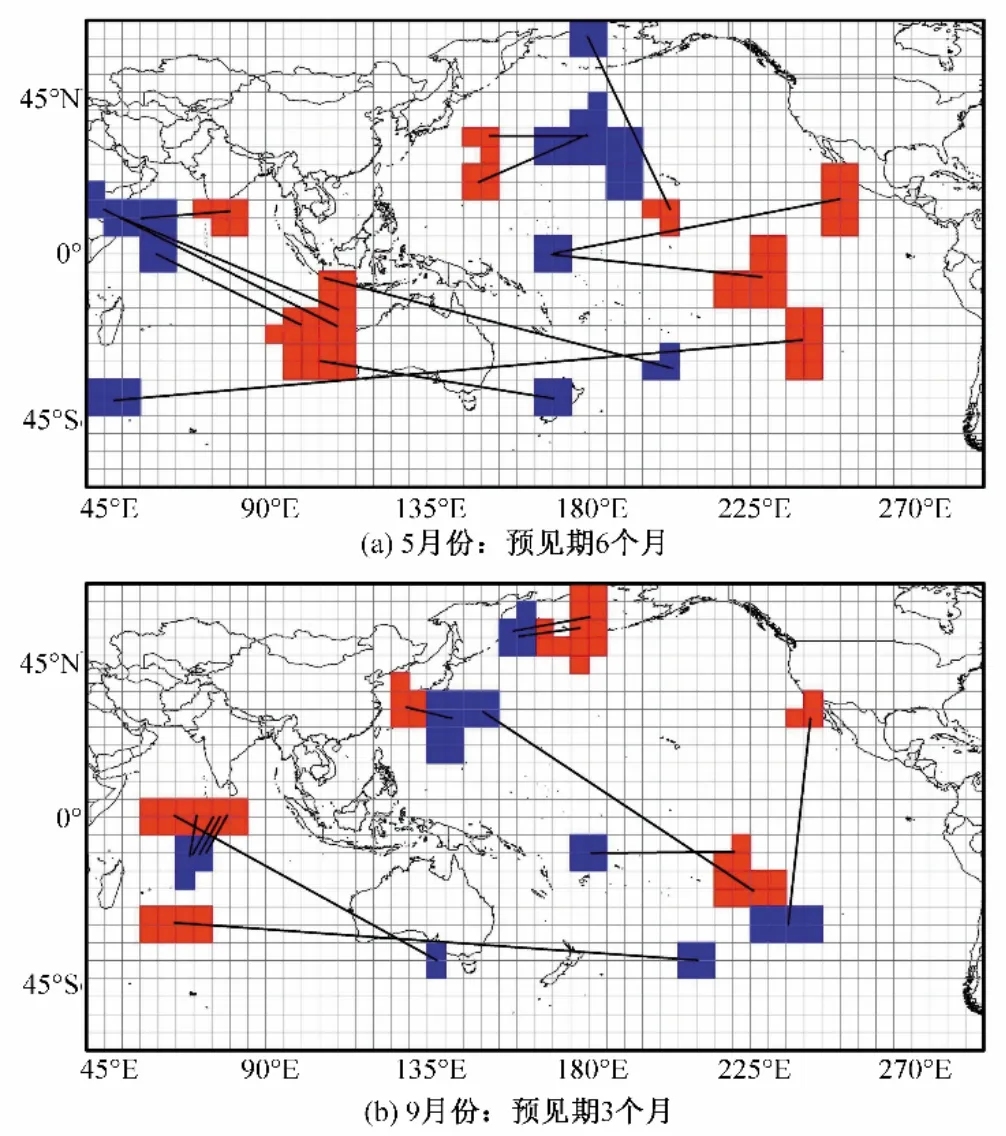
图2 对预见期为6个月时的5月份和预见期为3个月时的9月份筛选出的偶极位置分布图Fig.2 Selected SST dipoles for May at the 6-month lead time and for September at the 3-month lead time

考虑到天气系统的混沌性和随机性，引入不同来源的因子可能会产生噪声干扰从而影响预报精度，本研究向多元线性回归模型中逐步引入前期径流、大气环流和海温偶极因子，得到多种因子组合方案，如图3所示。图中以预报精度为评价指标，预报精度越高，颜色越蓝，反之则越红。由于仅考虑前期径流进行预报时只有个别月份能达到率定期修正复相关系数大于0.65 的要求，故在图中不予展示。图3（a）和（b）分别为预报因子只考虑大气环流和同时考虑径流和大气环流因子的情况。图3（c）到（f）为预报因子含有海温偶极的情况。由图可知，预报因子只考虑大气环流或考虑径流和大气环流因子时，在1 月份至4 月份的12 个预见期内仍可以达到较高的预报精度。以预报因子考虑径流和大气环流因子为例，1 月至4 月份12 个预见期的平均值分别为71.7、75.3%、65.8%和70.2%；而在5 月份、9月份和11 月的预报精度降至47.4%、47.9%和44.0%，特别是9月份和11月份，有多个预见期的预报精度低于40%。当预报因子考虑海温偶极因子、径流和海温偶极因子、大气和海温偶极因子以及径流、大气和海温偶极因子时［对应图3（c）到（f）］，9月份12 个月预见期的平均精度提升至了54.3%、55.0%、54.9%和55.6%，11 月份12 个月预见期的平均精度提升至了53.3%、53.3%、49.7%和49.7%。

图3 多元线性回归模型在预见期1-12个月的预报精度Fig.3 Comparison of prediction accuracy at lead times of 1 to 12 months among different predictor combinations

图4展示了6种预报因子组合在验证期12个月预见期的平均径流预报精度。预见期1 到3 个月时，预报效果最佳的因子组合为考虑径流和大气环流或考虑径流和海温偶极，3 个预见期2 种组合的预报精度分别为66.7%、66.8%，63.4%、63.9%，62.5%、62.3%。由此可见，尽管前期径流因子不能单独用作预报，但它的加入能提高大气环流因子和海温偶极因子单独使用时的预报精度，主要体现在预见期较短时。而含有海温偶极因子的预报因子组合，在预见期较长时预报效果较优。仅含有海温偶极因子或海温偶极与前期径流因子的组合，在预见期4 到11个月预报精度最优。当同时考虑径流、大气环流和海温偶极因子时，在各预见期的预报效果均不是最佳，可能是由于过拟合所导致的。

图4 各种预报因子组合在验证期的12个月预见期的平均预报精度Fig.4 Prediction accuracy of all predictor combinations at 1- to 12-month lead times in the validation period.

图5（a）和图5（b）分别展示了不同预报因子组合方式（与图3顺序一致）在天一水库汛期（5月至10月）和非汛期（11月至次年4 月）的径流预报效果。如图所示，在汛期，海温偶极对径流预测的指示性比大气环流因子强。过往研究表明中国夏季降水主要受夏季风异常影响，该夏季风来自印度洋，强度受印度洋海温异常影响［27-30］，可认为中国大部分流域汛期径流的变化与印度洋海温变化息息相关。图2 表明影响5 月和9 月的径流变化的最显著的偶极均主要分布在印度洋海域内，与相关文献一致。对于非汛期而言，在预见期4个月以内时，大气环流因子对径流预测的指示性远强于海温偶极因子，而当预见期超过4个月后，海温的指示作用超过大气环流。其主要原因是海洋记忆的时间尺度较长，海洋的温度变化远慢于大气，故海温异常对径流的作用的滞后时间要长于大气环流因子。从图中还可知，当预见期较短时（汛期预见期2 个月，非汛期预见期4 个月），引入流域的前期径流作为预报因子之一可以有效地提升预报效果，而当预见期较长时，引入前期径流对径流预测的指示作用消失。主要原因是通常当滞时超过3 个月时，月径流的偏自相关性就不再显著，可认为2 到4 个月前的径流对当前月份径流的影响很小，引入其作为预报因子无法提升预报效果。

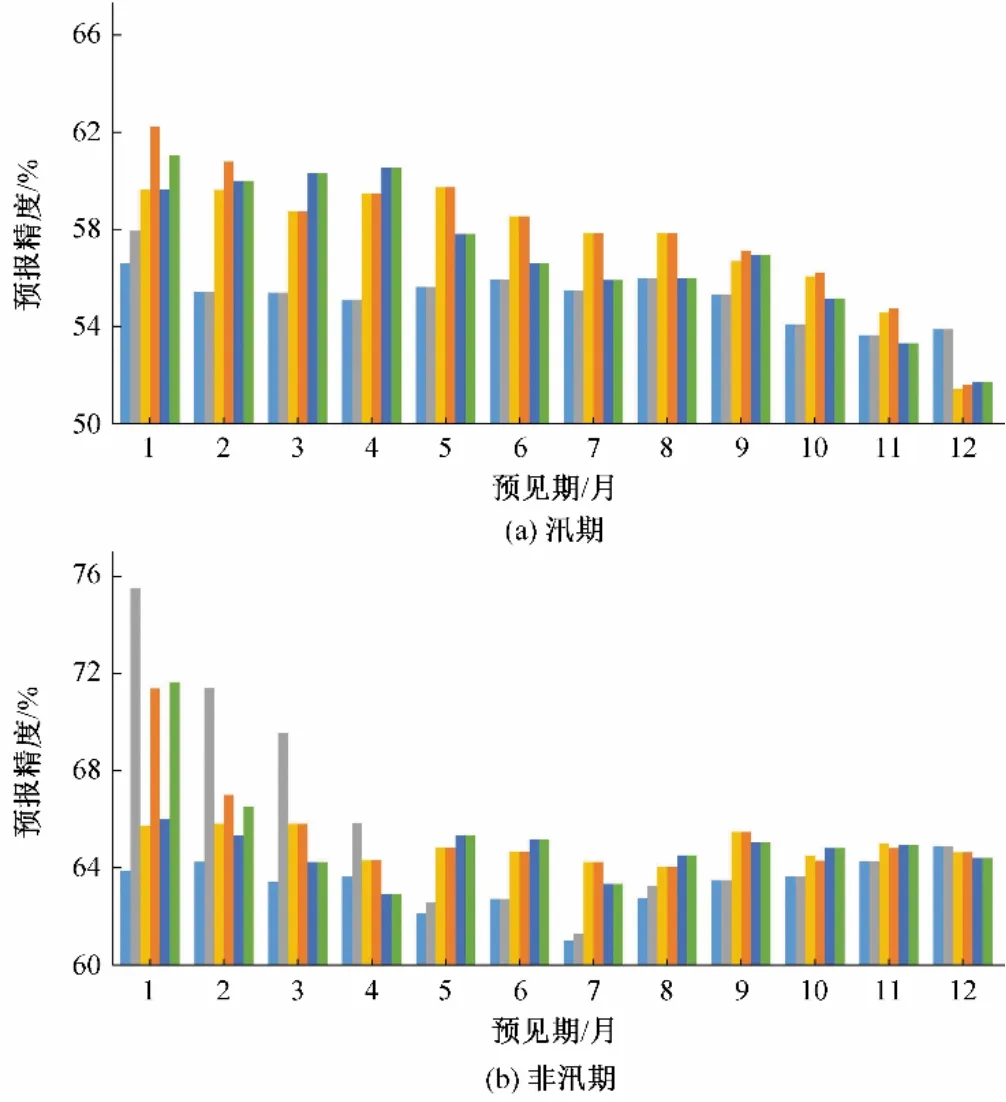
图5 各种预报因子组合在汛期和非汛期的预报精度Fig.5 Prediction accuracy of all predictor combinations at 1 to 12 month lead times in the flood season and non-flood season respectively

图6 展示了由2012 年12 月发起的2013 年全年的作业预报和由2017 年12 月发起的2018 年全年的作业预报径流过程线图，其中，黑色实线代表实测径流过程线。由图可知，各种因子组合预报径流量区别最大的月份为7 月至11 月。在预报2013年和2018年径流时，是否考虑径流作为预报因子对预报结果的影响较小。总体而言，预报因子考虑径流和海温偶极与仅考虑海温偶极的预报效果最好，模拟出了2018年汛期径流的双峰型特征。

图6 由2012年12月和2017年12月发起的12个月预见期的径流预报过程线图Fig.6 Streamflow predictions for 2013 and 2018 issued in December 2012 and December 2017， respectively

4 结 论

研究以天一水库为研究对象，基于多元线性回归方法在年内各月分别构建了预见期为1～12 个月的径流预报模型。在关键因子挑选部分以海温偶极取代了传统的固定海域的海洋表面温度场，并综合考虑了水库前期径流和大气环流对月径流预报的影响，主要结论如下。

（1）仅考虑前期径流作为预报因子时，月径流预报精度较差，但它的加入能提高大气环流因子和海温偶极因子单独使用时的预报精度，主要体现在预见期为1～3个月时。

（2）含有海温偶极因子的预报因子组合，在预见期较长时预报效果优于预报因子只考虑大气环流因子和考虑径流和大气环流因子的模型，其中以径流和海温偶极为预报因子的模型表现效果最佳，其在预见期为4～9 个月的平均精度较前述模型分别提升了2.4%和2.1%。此外，预报精度提升效果最为显著的月份为9月和11月，该模型对这两个月份在预见期1～12个月的平均精度较前述模型分别提升了8.2%、7.1%和12.6%、9.3%。