升力式飞行器集结轨迹实时规划方法

薛光伟，辛万青，傅 瑜

(1. 北京宇航系统工程研究所，北京 100076；2. 中国运载火箭技术研究院，北京 100076)

0 引 言

升力式再入飞行器是一种可以利用气动升力在大气层内进行无动力飞行的飞行器[1-2],是近年来各国学者的研究热点。升力式飞行器在飞行过程中面临着诸多干扰,包括参数、环境的不确定性,以及可能存在的冲突对抗,需要不断进行轨迹调整与恢复,过程中需要消耗能量;很多场景中,多个飞行器需要集结起来完成一些协同任务,而集结的过程同样需要调整轨迹,消耗能量。升力式飞行器无动力的特性决定了其可利用的机械能总量在飞行过程中无法增加,因此适应干扰的能力与集结飞行的任务之间存在矛盾。

对于升力式飞行器的集结轨迹规划问题,文献[3]利用神经网络生成倾侧角翻转控制指令,实现了升力式飞行器的时间协同;文献[4]推导了滑翔段高度、速度、航程等的高精度解析解,在此基础上引入粒子群算法和强化学习,实现了时间协同轨迹的在线优化求解。文献[3-4]设计的集结轨迹规划算法通过智能算法估计剩余时间,求解速度快,但其结果具有一定不可解释性。文献[5]根据预测能量和期望能量的关系,实时调整飞行攻角和升阻比,进而控制到达时间。文献[6]通过倾侧角幅值控制到达时间,通过攻角控制攻击角度,实现了多升力式飞行器的协同攻击。文献[7]把攻角固定为速度的线性函数,剩余时间通过轨迹仿真获得,迭代求解满足时间约束的攻角。文献[8]通过分析轨迹长度与到达时间之间的关系,设计了公共参考轨迹并利用线性二次型调节器进行跟踪,实现了升力式飞行器的多阵位协同再入。文献[5-8]所提出的集结轨迹模式中,飞行器需要在大部分航程中为实现协同而调整轨迹,这会带来较大的能量消耗,影响飞行器对于未知干扰的适应能力。基于伪谱法的轨迹优化方法是近年来的研究热点,理论上能够求出最优的集结轨迹。文献[9]提出了一种再入轨迹优化方法,通过自适应樽海鞘群算法改善伪谱法的全局寻优性能。文献[10]通过优化控制量变化率约束的处理方法,大幅提升伪谱法求解轨迹优化问题的计算效率。但远距离集结轨迹的规划问题更加复杂,状态空间更为庞大,应用伪谱法求解的实时性依然存在一定问题。

为提高飞行器应对未知干扰的能力,本文提出一种升力式飞行器集结轨迹规划方法。建立以能量为自变量的飞行器模型,分析了在平衡滑翔条件下升力式飞行器的最快到达轨迹模式与最慢到达轨迹模式,并提出最速能量调整轨迹的快速迭代计算方法。通过实时求解多个飞行器的可达时间范围,动态调整最终的集结时间,构建了多飞行器集结轨迹规划方法。

1 飞行器模型与集结轨迹分析

1.1 数学模型

考虑地球自转的影响,建立飞行器在极坐标系中的数学模型[11]:

(1)

式中:V飞行器为相对地球的速度,γ为飞行路径角,ψ为航向角,r为从地心到飞行器质心的距离,θ为经度,φ为地心纬度,m为飞行器质量,gr为引力加速度沿地心矢径方向的分量,gωe为引力加速度沿地球自转角速度方向的分量,ωe为地球自转角速度,D为气动阻力,L为气动升力,σ为倾侧角。

气动阻力和升力的计算公式如下[9]:

(2)

式中:Sref为飞行器参考面积,Cd,Cl为气动阻力系数和气动升力系数,ρ为大气密度。

以无穷远处为势能零点,定义飞行器单位质量的机械能E:

(3)

式中:μ为地球引力常数,Re为地球半径。

将能量对时间微分,可得:

(4)

由于升力式飞行器不带动力,只依靠最初的能量在大气层内飞行,且受到气动阻力影响,E在飞行过程中是不断衰减的,即dE/dt始终小于零。

1.2 可达时间范围

为了实现飞行器的集结,需要确定每个飞行器的可达时间范围,即飞行器抵达目标点的最晚到达飞行时间和最早到达飞行时间。

(5)

当剩余航程相同时,到达时间的上下界分别对应于平均速度的上下界。升力式飞行器的能量基本由速度决定[12],因此平均速度的上下界与平均能量的上下界相对应。

考虑能量航程剖面上的五条曲线,如图1所示。其中,曲线A与曲线E对应飞行器按照最大升阻比攻角飞行的轨迹,其中曲线A的终点为目标点,曲线E的起点为当前点。根据文献[13-14]可知,升力式飞行器按照最大升阻比攻角飞行时,航程最远,能量随航程衰减最慢。因此,最终能够抵达目标点的所有轨迹,不可能出现低于曲线A的点,否则将无法抵达目标点;而从当前点出发的所有轨迹,能量衰减速度不可能慢于曲线E,因此不可能出现高于曲线E的点。

图1 能量航程剖面轨迹示意图Fig.1 Trajectories in energy-range plane

曲线B、C、D分别对应三条从当前点到目标点的可行轨迹。曲线B代表的轨迹从当前点开始,以最大能力消耗能量,直到与曲线A相交,之后按照最大升阻比攻角飞行,轨迹与A重合。曲线D代表的轨迹前期与曲线E重合,在最后阶段以最大能力消耗能量,直到抵达目标点。曲线B和D其实就是从当前点到目标点所有可行轨迹的上下界,曲线C代表的就是B和D构成的可行域范围内任意一条可行轨迹。

结合图1易知,曲线B和D分别对应了平均能量的最小值和最大值,也就是最晚到达飞行时间和最早到达飞行时间。

1.3 最速能量调整轨迹

定义在满足平衡滑翔条件(飞行路径角基本保持不变[15])的前提下,以最短航程完成能量调整任务的轨迹为最速能量调整轨迹。曲线B和曲线D所代表的两条轨迹均由一段最速能量调整轨迹和一段最大升阻比轨迹结合而成。

以曲线B中的最速能量调整轨迹为例,假设轨迹终点能量为Eshift,速度为Vshift,轨迹长度微元dS可通过下式计算:

(6)

联立模型(1)、式(4)和式(6),可得飞行轨迹长度S相对于飞行器单位质量能量E的微分:

(7)

将式(7)积分:

(8)

在平衡滑翔条件下,可近似认为高度是能量的线性函数[16],即H=kE+a,其中k和a可通过初末状态求出,则有

(9)

由式(9)可知,轨迹长度S主要取决于阻力加速度系数Cd,Cd越大,S越小。

当高度差相同时,S越小,水平航程越短。水平航程可进一步分解为纵向航程和横向航程。为了便于分析,不妨假设飞行器沿赤道向东飞行,目标点在其正东方,则经度的变化为纵向航程,纬度的变化为横向航程,期望的偏航角ψ为90°,则能量管理段的纵向航程为

(10)

倾侧角取值对于阻力的变化影响并不明显,主要通过飞行路径角、偏航角影响纵向航程。如果要使能量管理段的纵向航程最短,则应使得γ0尽可能小,偏航角ψ尽可能偏离90°,而这都要求倾侧角幅值尽可能大,翻转次数尽可能少。为了同时满足能量管理段结束时的横向航程误差约束和偏航角误差约束,至少需要设置两次翻转进行规划[11]。

综合以上分析,为了实现最短纵向航程的能量管理,Cd和倾侧角幅值应取允许范围内的最大值,且设置两次倾侧角符号的翻转。

2 集结轨迹实时规划

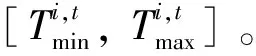
(11)

集结轨迹实时规划包含两部分内容,一是根据各飞行器状态实时确定集结时刻,这需要对各飞行器的可达时间范围的进行求解;二是根据集结时刻调整各飞行器的轨迹。

2.1 可达时间范围求解

最慢到达轨迹对应于图1中的曲线B,由一段最速能量调整轨迹与一段最大升阻比轨迹构成。

最大升阻比轨迹以目标点为终点,可以预先确定。最速能量调整轨迹则需迭代求解。

4)迭代次数z=z+1,判断若超出最大迭代次数,则计算结束;未超出则执行下一步。

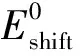
(12)

式中:kS为调整系数,可控制迭代的速度,在0到1之间取值,越大则航程收敛越快,可根据航程与误差需求选取适当的值。

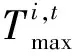
(13)

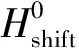
根据平衡滑翔条件[15]可知,飞行路径角随时间变化率等于零,则倾侧角幅值可通过下式计算:

(14)

倾侧角翻转位置以及最速能量调整轨迹航程的求解方法与最慢到达轨迹相同,此处不再赘述。

2.2 集结轨迹规划方法

(15)

式中:Tf0即为最初确定的集结时间。

飞行过程中的集结轨迹实时规划共分为两个阶段。其中第一阶段的任务是确定最终的集结时间,第二阶段是各飞行器按照集结时间调整自身轨迹。

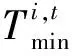
(16)

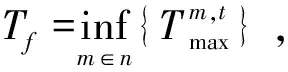
进入第二阶段后,飞行器j需要转入曲线B代表的最慢到达轨迹模式,消耗多余能量,降低速度,否则将无法与飞行器i的集结。能量调整段结束后,飞行器j必须沿能量最优轨迹飞行,不再具备多余能量。飞行器若在此阶段遭遇敌对干扰,需要根据实际情况与预先设定的规则,在机动与集结之间进行取舍,因为进行机动将导致其到达时间延后,抵达集结点的速度也将低于集结要求。

飞行器i则继续沿曲线D代表的最快到达轨迹飞行,保持快速飞行,但必须将多余能量集中在最后的能量调整段消耗,在此之前不可再做额外机动;此时如果再次遭遇干扰,虽然仍有多余能量,额外的机动不一定影响其终端速度,但会导致抵达时间延后,错过预定的集结时间。

其他飞行器则以此集结时刻Tf为目标,当最早到达飞行时间大于Tf时,停止额外机动,沿最快到达轨迹飞行;当最晚到达飞行时间小于Tf时,转入最慢到达轨迹。

最终,所有飞行器将在Tf时刻抵达集结位置。整个集结飞行的流程如图2所示。

图2 集结轨迹实时规划流程图Fig.2 Flow chart of gathering trajectory planning algorithm

3 仿真分析

为了验证本文提出的集结轨迹规划方法,考虑三架升力式飞行器CAV-H[18]进行集结的场景。飞行器分别从不同位置出发,需要在相同的时间点抵达各自的集结点完成集结任务。

为了便于观察轨迹规划方法的效果,不妨假设3架飞行器从初始点出发和抵达各自集结点时的高度、速度、飞行路径角、航向角均相同,但是纵向与横向的航程不同。各飞行器的初始状态与目标状态如表1所示。仿真中涉及的所有时间、高度、速度、航程已无量纲化处理。不同的是飞行器A会在飞行过程中遭遇三次未知干扰,飞行器B则不会。

表1 各飞行器的初始状态与集结状态Table 1 The initial state and terminal gathering state of each vehicle

按照本文所提出的方法,计算三个飞行器在起滑初始时刻的最早到达时间为:0.666,0.635,0.607。

因此,将三个飞行器的发射时间分别调整为0,0.031,0.059,此时三者的最快与最慢到达轨迹如图3所示。

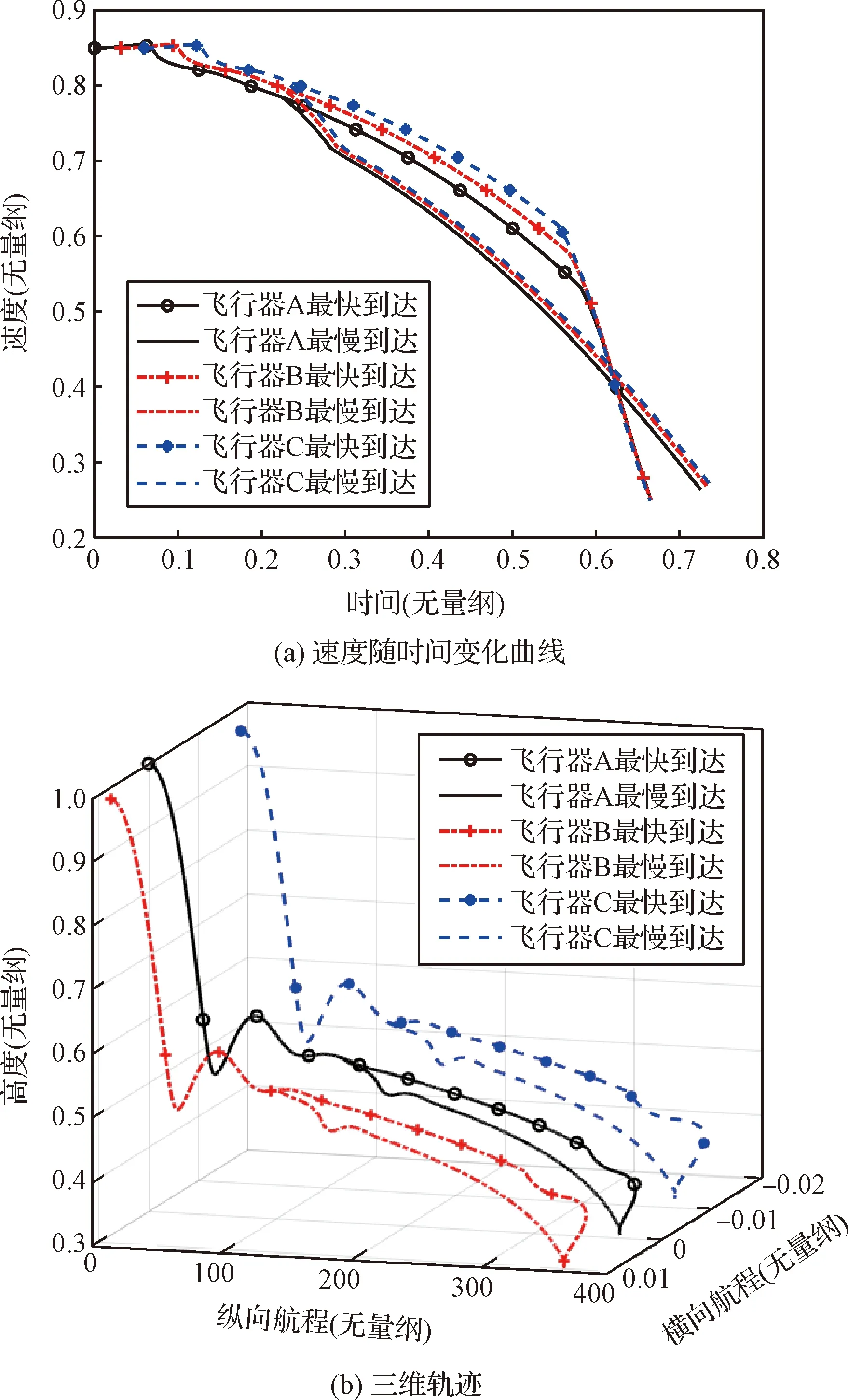
图3 初始时刻的最快到达轨迹与最慢到达轨迹Fig.3 The fastest and slowest trajectories at beginning

所有飞行器在飞行过程中都会实时解算自身的可达时间范围。通过仿真发现,单次解算耗时不超过5 s,因此可以设置沟通规划集结时间的周期为10 s。

在飞行过程中,飞行器可能遭遇敌对飞行器的干扰,飞行器采用S机动策略进行应对。机动期间,飞行器攻角取最大值20°,倾侧角幅值取60°,倾侧角符号按固定频率翻转,使得飞行器在射面左右摇摆机动。在本文的仿真场景中,假设飞行器A未遇到干扰,飞行器B于0.375(无量纲化时间)遭遇一次干扰,飞行器C则于0.25、0.35、0.425和0.45遭遇了四次干扰,如图4所示。

图4 飞行器机动期间的攻角与航向角Fig.4 Angle of attack and heading angle of vehicles during maneuvering

这些干扰使得B、C的轨迹逐渐偏离了初始时刻的最快到达轨迹,能量也越来越偏离初始能量最优轨迹,因此最早到达时间渐次增大。同时,飞行器A一直按照最快到达轨迹飞行,其最晚到达飞行时间逐渐减小。最终在0.525,飞行器A的最晚到达时间早于飞行器C的最早到达时间,集结时间确定为0.686,集结轨迹规划第一阶段完成,各飞行器转入第二阶段飞行。

在第二阶段中,飞行器A切换到最慢到达轨迹,飞行器C继续按照最快达到轨迹飞行,不再执行额外机动动作。飞行器B继续保持能量最优轨迹飞行,直到0.545时,其最晚到达时间也小于0.686,转入最慢到达轨迹。最终,三架飞行器基本同时到达集结位置,完成集结,如图5所示。

图5 飞行器的实际集结轨迹Fig.5 The actual gathering trajectories of vehicles

通过图5(b)的能量曲线可以看出,本文设计的集结轨迹规划方法使得飞行器B与飞行器C的富余能量充分应用在了应对突发干扰的机动中,整个飞行器集群始终保持能量最优的态势飞行,直到集群状态抵达可实现集结的边界,在整个集群尺度上实现了能量的优化分配。

图6展示了整个集结过程中的路径约束满足情况,可以看到所有飞行器的热流、动压、过载均未超出约束(约束上限均为1)。这是由于飞行器全程采用拟平衡滑翔模式,轨迹变化一直比较平缓,最可能超出约束的是末段的能量调整段。一旦超过约束,则需要通过改变能量调整段的攻角,减缓能量调整的速度,实现路径约束的满足。

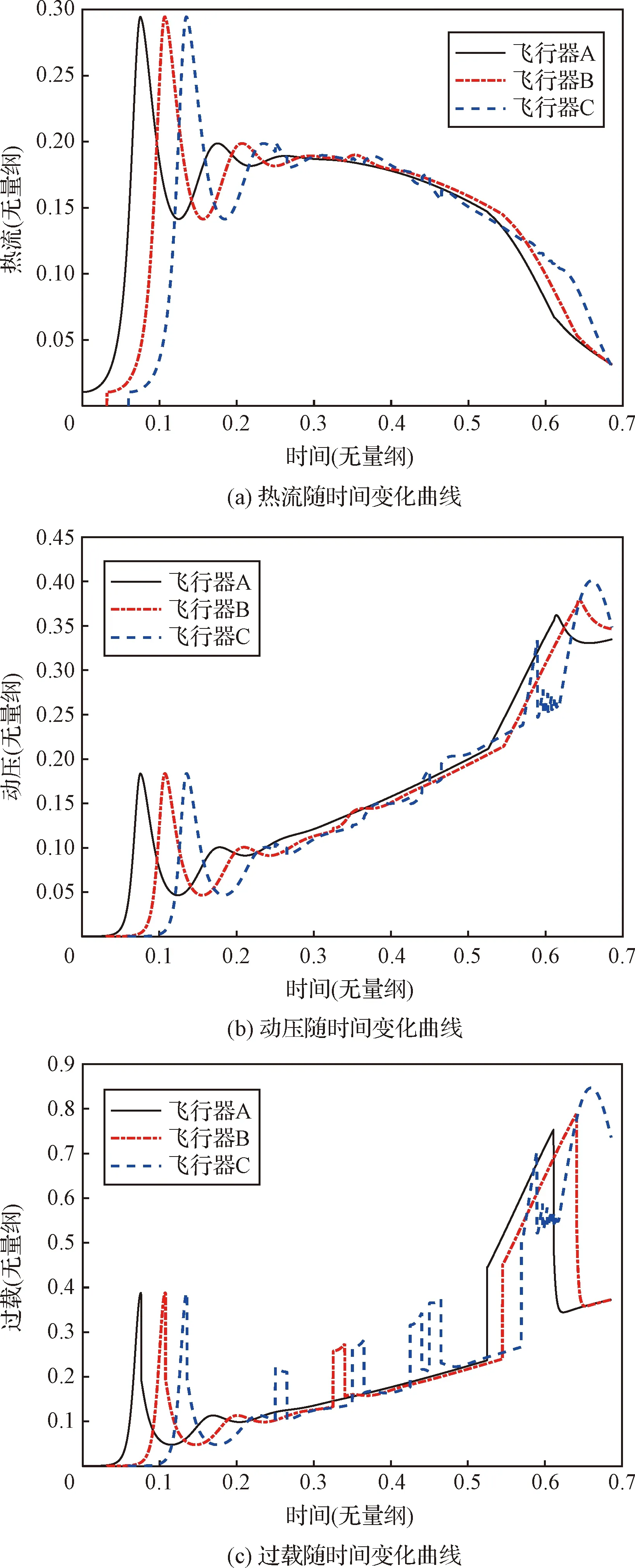
图6 热流、动压、过载曲线(无量纲)Fig.6 The heat, dynamic pressure and load curve

4 结 论

本文针对升力式飞行器的集结问题,提出了一种能够提高飞行器干扰适应能力的实时轨迹规划方法,并通过仿真验证了算法的有效性。

1)本文提出了一种集结轨迹规划方法,通过实时求解可达时间范围协调多个升力式飞行器的集结时间。通过仿真分析,证实这种轨迹规划方法能够实现升力式飞行器面对严重干扰时的集结飞行,提升飞行器执行任务的适应性。

2)本文分析了在平衡滑翔条件下升力式飞行器的最快到达轨迹模式与最慢到达轨迹模式,提出了最速能量调整轨迹的快速迭代计算方法,构建了多飞行器集结轨迹规划方法,通过仿真验证了方法的可行性。