行星动力下降多约束最优反馈制导方法

张晓文，王天舒，王大轶，李 骥

(1. 清华大学航天航空学院，北京 100084；2. 北京控制工程研究所，北京 100190；3. 北京空间飞行器总体设计部，北京 100094)

0 引 言

未来行星着陆探测任务普遍提出定点着陆的工程目标,一般要求落点精度为100 m。实现此目标主要依靠动力制导。以往月球和火星着陆器的动力制导方法研究和工程应用多采用多项式制导,例如阿波罗制导和E制导。阿波罗制导的优点是终端三维位置、速度和加速度全部受控,缺点是固定终端时刻后未对推进剂消耗作优化。Lu[1-2]为改进阿波罗制导,先是参考隐式制导在原制导律中增加了一个控制增益作为可调参数,之后应用分数多项式理论又增加了分数指数参数,并将新方法命名为分数多项式动力下降制导。阿波罗制导中发动机推力加速度为时间的二次多项式形式。经典的E制导及与其等同的基本型ZEM/ZEV制导[3]的推力加速度的制导指令为时间的一次多项式形式。E制导已被证明是常值引力场假设下的固定终端时刻的加速度模平方积分最优制导[4],即能量最优制导,虽然不能完全等同于推进剂消耗最优,但是已经对推进剂消耗做了显著优化。E制导的一项缺点是终端三维加速度不完全受控。E制导和阿波罗制导都未考虑推力范围限制,因此实际应用中指令推力可能触发推力饱和。

E制导或基本型ZEM/ZEV制导尽管是最优反馈制导,但是面对实际工程应用时还是存在一些不足,因此对其改进的方法不断被提出。这些改进包括完善最优制导时长确定方法,提高制导算法的鲁棒性和碰撞规避能力等。Guo等[5]使用数值优化程序GPOPS选择中间航路点作为ZEM/ZEV制导的中间目标,实现了火星动力下降约束下滑角的碰撞规避。Zhou等[6]针对火星动力下降段制导规避碰撞地平问题,在ZEM/ZEV制导原性能指标中添加了加权的高度项,然后推导出有地平碰撞规避能力的改进制导律。Wibben等[7]为了提高ZEM/ZEV制导在火星动力下降段的干扰适应性,加入最优滑动制导并证明了新方法的全局稳定性。Zhang等[8]利用平均加速度修正基本型ZEM/ZEV制导加速度的来解决月面着陆地平碰撞规避问题,还应用模型预测静态规划(MPSP)方法迭代计算满足终端状态约束的解。Zhang等[9]对Zhou等[6]的方法继续改进,将性能指标中高度项的常值加权系数改为与高度平方相关的时变系数,进一步提升碰撞规避能力。Ahn等[10]研究了轨道拦截或交会机动问题的由最小能量和最小时间组成的性能指标,利用最优控制理论和横截条件,推导出确定ZEM/ZEV制导最优制导时长的代数方程。Wang等[11]提出一种适用于火星精确着陆的两段ZEM/ZEV反馈制导方法,通过虚拟终端速度和在线参数搜索来提高制导的障碍规避能力。高峰等[12]利用脉宽脉频(PWPF)调制器将ZEM/ZEV制导的连续指令转换为常值推力器的开关指令。

碰撞规避是行星着陆制导必须具备的能力。除了上面提到方法外,还有一种解决思路是控制着陆轨迹的曲率。Cui等[13]先是提出了一种基于多项式的曲率制导策略,通过调整曲率使着陆器沿凸形轨迹着陆,降低障碍物碰撞的风险。之后进一步改进,将曲率约束凸化为二阶锥约束,并利用非线性规划工具求解凸规划问题来优化推进剂消耗[14]。

近年来数值优化方法和人工智能技术被越来越多的应用于行星着陆制导问题的理论研究中。林晓辉等[15]应用凸优化理论将月球动力下降段轨道优化问题转化为二阶锥问题,并采用内点法求解了最优标称轨迹。邓雁鹏等[16]应用序列凸优化方法解决月面动力下降过程中时变加速度剖面实时估计和补偿问题。Furfaro等[17]将深度强化学习方法与ZEM/ZEV制导方法相结合,通过动态调节2个制导增益和制导时长来满足行星着陆问题的路径等约束并优化推进剂消耗。数值优化制导计算量大,依赖高效稳定的求解器。人工智能制导目前处于理论研究阶段,工程应用同样面临计算量大和算法稳定性方面的挑战。

总体而言,传统最优反馈制导方法有着计算量小、稳定性好、节省推进剂的优势,但是仅满足初始和终端位置速度约束。实际工程应用中还需要考虑推力范围受限、连续变推力、碰撞规避和终端加速度等多方面约束。单台变推力发动机推力的大小和方向在物理上只能连续变化,因此要求制导的指令推力连续变化。着陆终端希望着陆器为竖直姿态,并且合加速度接近为零,这就对制导的终端加速度提出了约束。现有最优反馈制导方法研究欠缺对上述约束的综合考虑。

本文考虑推力范围受限、连续变推力、碰撞规避和终端加速度共4方面约束,对动力下降应用的传统最优反馈制导方法进行改进和完善。内容安排为,首先建立行星定点着陆动力下降制导问题模型,然后介绍和分析E制导和阿波罗制导方法,接着详细阐述提出的多约束最优反馈制导方法,最后通过数学仿真验证所提方法有效性。

1 问题模型

1.1 制导坐标系定义

制导坐标系原点O定义在目标着陆点,从原点指向天向定义为Z轴,垂直Z轴从原点指向着陆器初始位置方向为X轴,Y轴按照右手螺旋法则确定。在该坐标系下,XOZ平面即为理想着陆轨迹面,或又称为纵向平面,Y轴即为轨迹面负法线方向。X轴位移体现着陆器航程变化,因此可以将X向称之为航向,Z轴位移体现着陆器高度变化,Y轴位移体现着陆器垂直轨迹面位置变化,因此可以将Y向称之为横向。

1.2 行星动力下降动力学方程

月球没有大气。火星大气稀薄,在着陆器动力下降段气动力显著小于制导推力。因此以往分析行星动力下降制导问题时忽略大气影响,仅考虑中心天体引力和发动机推力。制导坐标系下的行星动力下降动力学方程如下:

(1)

(2)

a=F/m

(3)

(4)

1.3 定点着陆制导问题

定点着陆制导问题即控制着陆器以指定终端速度到达指定终端位置。研究定点着陆制导问题时一般将终端位置和速度取为零。定点着陆制导问题属于轨迹优化问题,轨迹优化问题又属于最优控制问题。设初始时刻为0,下面依次列出定点着陆制导问题的初始条件、终端条件、性能指标和推力约束表述。

初始条件:

r(0)=r0

(5)

v(0)=v0

(6)

m(0)=m0

(7)

终端条件:

r(tf)=rf

(8)

v(tf)=vf

(9)

性能指标:

(10)

推力约束:

Fmin≤F≤Fmax

(11)

2 多项式制导

多项式制导即制导指令加速度为时间的多项式形式。常见的多项式制导有E制导和阿波罗制导。下面对E制导和阿波罗制导展开原理介绍和性质分析。在做性质分析时假设引力加速度为常值。

2.1 E制导

在E制导方法中,制导推力加速度三维矢量取为时间的一次多项式,包含2个待确定系数矢量,即指令推力加速度为

a=c0+c1t,t∈[0,tf]

(12)

将式(12)代入动力学方程(2)中,然后连续积分两次,并代入位置速度的初值和终值确定制导律系数,结果如下:

(13)

(14)

将式(13)代入式(12)中后,得到E制导的初始时刻推力加速度计算公式:

(15)

定义零控位移偏差rzem和零控速度偏差vzev如下:

(16)

vzev≜vf-v0-tfg

(17)

代入式(15)中,得到零控位移偏差rzem和零控速度偏差vzev形式的制导指令推力加速度计算公式,即基本型ZEM/ZEV制导律公式:

(18)

上式说明E制导与基本型ZEM/ZEV制导完全相同。将零控位移偏差rzem和零控速度偏差vzev前的常值控制增益6和-2改为可调控制增益kr和kv,则得到了一般型的ZEM/ZEV制导律公式[18]:

(19)

利用庞特里亚金极小值原理可以证明,E制导是常值引力场假设下的加速度模平方积分最优制导,即能量最优制导,使得如下性能指标最小:

(20)

E制导性质1.E制导的单个方向推力加速度为单调变化。

(21)

E制导性质3.已知初始高度大于零,即rz0>0,在t∈[0,tf),满足rz>0的条件为

(22)

2.2 阿波罗制导

在阿波罗制导方法中,制导加速度三维矢量取为时间的二次多项式,包含3个待确定系数矢量,即指令推力加速度为

a=c0+c1t+c2t2,t∈[0,tf]

(23)

将式(23)代入动力学方程(2)中,然后连续积分两次,并代入位置、速度和加速度的初值和终值确定制导律系数,结果如下:

(24)

(25)

(26)

将式(24)代入式(23)中后,得到E制导的初始时刻推力加速度计算公式:

(27)

由阿波罗制导的求解过程可知,求解常值制导参数时用到了终端位置、速度和加速度条件,因此与E制导相比,阿波罗制导除了可以满足终端位置和速度约束外,还可以满足终端加速度约束。

3 多约束最优反馈制导

3.1 制导时长寻优算法

多约束最优反馈制导的基础是E制导,也即基本型ZEM/ZEV制导。E制导给出了终端时刻固定的指令加速度计算公式,没有给出终端时刻的确定方法。如果制导加速度允许范围不受约束,则E制导的终端时刻可由E制导性质2,即式(21)确定,保证了制导加速度模平方的积分最小。工程应用中制导加速度允许范围一定受限。一般来讲,制导时长越短越节省推进剂[6],但是推力变化范围也会随之变大,最终指令推力超过了发动机实际允许范围,即指令推力饱和。考虑推力范围约束后,实际输出推力矢量满足如下公式:

(28)

E制导有解析的轨迹预报公式,理论上只要终端指令推力不饱和,则规划轨迹满足终端状态约束。因此,将终端指令推力不饱和作为制导算法基本原则。在此基础上尽量缩短制导时长作为优化推进剂消耗的方向。最优制导时长参数难以通过解析计算公式直接获得,因此这里采用数值方法来寻找。优化制导时长首先需要给出其一个合理的初值tf0。该初值应尽量接近最优值又要便于计算。这里提出将使得初始指令推力正好等于允许最大推力的制导时长作为优化初值tf0。设rf=0和vf=0,由式(15)推导得到E制导的推力加速度模平方的初值为

(29)

由最大允许推力Fmax和初始质量m0得到最大允许初始加速度为a0max=Fmax/m0。将最大允许初始加速度a0max代入式(29)得到制导时长tf的4次方程:

(30)

利用解析公式求解该方程,将其中最大实数根作为制导时长初值tf0。将制导时长初值tf0代入E制导公式,进行首次数值积分预报,得到终端时刻标称推力指令。如果终端指令推力饱和,则需要增加制导时长。这里采用预测校正方法来计算增加量。记数值积分预报给出的指令推力在制导末端持续饱和的时长为tfs,校正系数记为ka,则给出制导时长第1个校正公式如下:

tf,i+1=tf,i+katfs

(31)

式中:下标i为迭代计算拍数。将校正后制导时长再次代入制导方程,重新进行数值积分预报。当终端指令推力不再饱和时认为制导时长优化完成。

如果首次数值积分预报的终端指令推力未饱和,则说明制导时长还可以缩短。记制导时长缩短系数为ks,则制导时长缩短公式如下:

tf,i+1=kstf,i

(32)

应保证制导时长缩短足够充分,使得终端指令推力一定饱和。

接下来再次进行数值积分预报。仍然采用预测校正方法来计算增加量。记校正系数为kb,则给出制导时长第2个校正公式如下:

tf,i+1=tf,i+kbtfs

(33)

校正系数ka和kb取值偏小的话,则单次修正量过小,需要的迭代计算次数多。校正系数取值偏大的话,则单次修正量过大,计算得到制导时长比其最优值偏大较多。

定义推力俯仰角为推力方向和天向的夹角。为避免着陆器大幅度姿态机动带来多方面不利影响需要约束推力俯仰角。通常不希望推力俯仰角超过90°,对应的等效条件是垂向推力加速度非负。由垂向推力加速度非负得到的制导时长的不等式约束为:

(34)

显然该式给出了一个制导时长的最小值约束。

3.2 碰撞规避算法

碰撞地面风险规避要求飞行高度不低于地面。由E制导性质3得到制导时长需满足不等式(22),因此定义碰撞规避时长如下

(35)

式中:vzmin为足够小的速度阈值,避免除零。

为规避碰撞地平风险,计算垂向制导加速度时,制导时长计算公式如下:

(36)

依据上式得到新的制导加速度,进行数值积分预报。如果推力没有饱和,那么用上式方式来制导可以实现临界碰撞规避。但是实际推力很可能初始就饱和,且上式取值临界,此时碰撞规避就很可能已经来不及。这种情况下需要进一步优化推力加速度的分配。由于碰撞规避的优先级高,因此推力饱和时,优先满足垂向的推力加速度需求。给出碰撞规避控制的推力优化分配律如下:

(37)

(38)

式中:m为着陆器当前质量;amax为当前最大允许推力加速度;ax、ay和az为加速度优化分配前指令加速度三轴分量,且az≥0;F为优化分配后的指令推力矢量。

为了进一步提高着陆安全性,增加碰撞规避的裕度,可以再增加下滑角约束,即着陆器与目标着陆点连线,与地平的夹角需大于阈值。在满足地平碰撞规避的基础上,下滑角约束通过坐标系旋转的方法即可方便的得到满足[11]。记下滑角阈值为α,则由制导坐标系到下滑角坐标系的旋转阵为

(39)

将初始位置矢量r0和速度矢量v0,终端目标位置矢量rf和速度矢量vf,引力加速度矢量g,都左乘坐标系旋转阵Cgl,得到下滑角坐标系对应的分量。将经坐标系旋转变换后的变量作为新的初始约束、终端约束和引力加速度矢量代入制导计算公式便可得到满足下滑角约束的解。满足下滑角约束后既提高了碰撞规避能力又增加了着陆点可见性。

3.3 匀速转动制导

着陆终端一般希望着陆器为竖直姿态并且合加速度近似为零,即推力加速度应为负的引力加速度。这就对制导的终端加速度提出了约束。但是如前所述,E制导的终端三维加速度不完全受控,即不能满足该约束。为了满足终端加速度约束,在E制导结束之后,引入匀速转动制导,迅速调整推力加速度到目标值。

匀速转动制导的功能是依据最大角速度和最大推力变化率约束实现最短时间内调整推力加速度矢量的方向和大小。匀速转动制导的指令推力在由初始和终端加速度确定的平面内匀速转动。匀速转动制导的输入为初始制导加速度a0和终端目标加速度af,输出为指令推力F、制导时长tf、位置增量Δr和速度增量Δv。初始制导加速度a0和终端目标加速度af的夹角为:

(40)

(41)

定义匀速转动制导的平面坐标系为:原点为推力作用点,X轴为初始制导加速度方向,X轴向终端目标加速度方向旋转90°得到Y轴。

匀速转动制导的原理是首先计算平面坐标系下推力加速度矢量,然后将其转换为三维坐标系下矢量。最终的匀速转动制导的指令推力计算公式为:

(42)

F0=m0||a0||

(43)

Ff=mf||af||

(44)

θ=θft/tf

(45)

式中:M为将平面坐标系矢量转为三维坐标系矢量的转换阵;mf为着陆器在制导终端的质量,可以用初始质量m0近似代替。

对合加速度做一次和二次积分分别得到位置增量Δr和速度增量Δv的解析表达式:

(46)

(47)

图1 组合制导参数预测校正规划方法示意Fig.1 Diagram of predictor-corrector planning method for integrated guidance parameters

最优反馈制导和匀速转动制导交接处的位置rm和速度vm的校正公式如下:

rm=rf-Δr

(48)

vm=vf-Δv

(49)

4 仿真校验

以火星探测任务的动力下降段为例,通过数学仿真方法来验证和分析新提出的制导方法。仿真用例选取时参考了文献[5,7,9,11]中的共同用例。着陆器的初始质量取为1 905 kg,发动机比冲取为2 205 Ns/kg,制导坐标系下的初始位置为[2 000, 0, 1 500]Tm,初始速度的多组工况在后面分别给出;目标终端位置为[0, 0, 0]Tm,目标终端速度为[0, 0, 0]Tm/s,目标终端加速度为[0, 0, 0]Tm/s2。发动机推力最大值为13.258 kN,最小值为4.971 kN。火星引力加速度取为[0, 0, -3.711 4]Tm/s2。校正系数ka和kb的取值分别为0.7和0.3。制导时长缩短系数ks取为0.5。

4.1 有效性验证

设计制导有效性验证仿真工况对3.1节中方法做验证,设定了4组初始速度取值,详见表1。

表1 有效性验证仿真工况的初始速度Table 1 Initial velocities of effectiveness verification simulation cases

有效性验证仿真工况的轨迹见图2。从图中可知,4条轨迹的初始位置相同,由于初始速度不同导致中途轨迹不同,不过最终都汇集到了坐标系原点,即目标终端位置。比较工况2到3的制导飞行轨迹,当航向初始速度为负值时,制导飞行轨迹偏左上,航向初始速度为正值时,制导飞行轨迹偏右下。比较工况3和4的制导飞行轨迹,当垂向和航向初始速度相同,有横向初始速度时,制导飞行轨迹将偏右下。有效性验证仿真工况4的横向位置速度曲线见图3。从中可知,横向位置偏差先增大然后逐渐减小到零,横向速度偏差先由正值变为负值然后逐渐减小到零。有效性验证仿真工况的推力比见图4。从中可知,初始航向和横向速度越大则制导时长越长,初始推力饱和时长也越长。工况1、3和4的推力由饱和段、减小段和增加段组成,即推力大致按照大小大的趋势变化,近似于最优控制理论给出的变推力制导的最大最小最大推力剖面[19]。工况2虽然没有推力饱和段,但是推力符合大、小、大的变化趋势。有效性验证仿真工况的推力俯仰角见图5。从图中可发现推力俯仰角的2个变化规律。第1个规律是推力俯仰角先大后小然后再增大,原因是着陆器为了实现水平方向的位移,需要在水平方向上先加速然后再减速。第2个规律是初始航向和横向速度越大则初始推力俯仰角越大,原因是制导需要在水平方向分配更多的推力来抵消初始的反向水平速度。

图2 有效性验证仿真工况的轨迹Fig.2 Trajectories of effectiveness verification simulation cases

图3 有效性验证仿真工况4的横向位置速度Fig.3 Cross position and velocity of effectiveness verification simulation case 4

图4 有效性验证仿真工况的推力比Fig.4 Thrust throttles of effectiveness verification simulation cases

图5 有效性验证仿真工况的推力俯仰角Fig.5 Thrust pitch angles of effectiveness verification simulation cases

制导有效性验证仿真工况的制导时长和推进剂消耗仿真结果见表2。从表中可知,初始航向和横向速度越大则制导时长和推进剂消耗越长和越多。工况2由于初始航向速度与目标水平移动方向相同,因而制导时长最短并且推进剂消耗最少。表中给出了预测校正法和遍历法两种方法的推进剂消耗来对比。遍历法的搜索步长取为1 s。可以看出,预测校正法的推进剂消耗十分接近遍历法,最大仅相差1.1%。表中还给出了两种预测校正的实际迭代次数。工况1实际执行式(31)所示的预测校正0次,执行式(33)所示的预测校正2次。工况2实际执行式(31)所示的预测校正1次,执行式(33)所示的预测校正0次。所有4个工况仅需执行1到2次预测校正便可获得满意的结果,说明所提出的预测校正方法不仅有效而且高效。

表2 有效性验证仿真工况的制导时长和推进剂消耗Table 2 Time-to-go and fuel consumption of effectiveness verification simulation cases

4.2 碰撞规避验证

文献[5,9,11]中为了测试验证制导算法碰撞规避性能,设计了恶劣的碰撞规避仿真工况,初始速度取为[100, 0, -75]Tm/s。在此初始速度条件下,分别按照无碰撞规避、有地平规避、有8°下滑角约束和有9°下滑角约束进行制导方法的测试仿真,对比验证3.2节中的碰撞规避方法。碰撞规避仿真工况的轨迹见图6。从中可知,无碰撞规避的制导飞行轨迹有部分位于了地平线下,该结果意味着着陆器将与地面碰撞。考虑地平规避的制导飞行轨迹在着陆后期紧紧贴着地平,实现了临界的碰撞规避,该结果具有理论分析意义,但是不能用于实际飞行,因为其安全裕度不够高,实际地面必然是具有一定幅度的起伏。有8°和9°下滑角约束的着陆轨迹可以明显看到着陆后期保持了一定的飞行高度,与地平线形成了固定夹角,显然该飞行轨迹的碰撞规避裕度更高,对一定幅度的地形突起也可以实现碰撞规避,因而更具有工程应用价值。工况2到4的高度是单调变化的,另外着陆后期的轨迹线为直线,原因是着陆后期在下滑角坐标系下垂向速度已被控制到零。文献[5]利用航路点方法作碰撞规避的后期航迹也近似直线,然而航路点前后制导推力不连续。文献[9,11]中碰撞规避段的高度是先探底然后上升之后再下降,也就是高度非单调下降,并且文献[11]中也有制导推力跃变点。碰撞规避仿真工况的垂向速度见图7,从中可知,工况1的垂向速度先为负值后为正值,工况2和3的垂向速度全程为非正值,工况4的垂向速度先为负值中间为正值后为负值。工况4的垂向速度出现正值的原因是在碰撞规避控制段的推力始终饱和。碰撞规避仿真工况的推力比曲线见图8,从中可知,全部工况的推力由饱和段、减小段和增加段组成,即推力大致按照大小大的趋势变化。比较工况2到4可知,碰撞规避的约束下滑角越大,制导时长越长。另外,考虑碰撞规避后制导初期的推力饱和段时长增大,并且碰撞规避裕度越大,制导初期推力饱和段时长增大的越多。碰撞规避仿真工况的推力俯仰角见图9,从中可知,碰撞规避要求越严格则推力的初始俯仰角越小,如果初始推力饱和则初始俯仰角等于负的下滑角。该现象的原因是,为了实现碰撞规避就需要减小下降速度,因此制导算法在垂向分配的推力更大,因此推力俯仰角就会相对变小。工况4的推力俯仰角在30 s时发生3.1°的跃变,原因是碰撞规避控制结束时刻已到,但是推力还处于饱和状态,因此导致制导加速度变化不连续。工况4说明如果希望制导推力连续,则在碰撞规避控制结束时制导推力应处于非饱和状态。工况3在保证指令推力连续的前提下满足了8°下滑角约束,大于文献[5,11]中相同条件下实现的4°。

图6 碰撞规避仿真工况的轨迹Fig.6 Trajectories of collision avoidance simulation cases

图7 碰撞规避仿真工况的垂向速度Fig.7 Vertical velocities of collision avoidance simulation cases

图8 碰撞规避仿真工况的推力比Fig.8 Thrust throttles of collision avoidance simulation cases

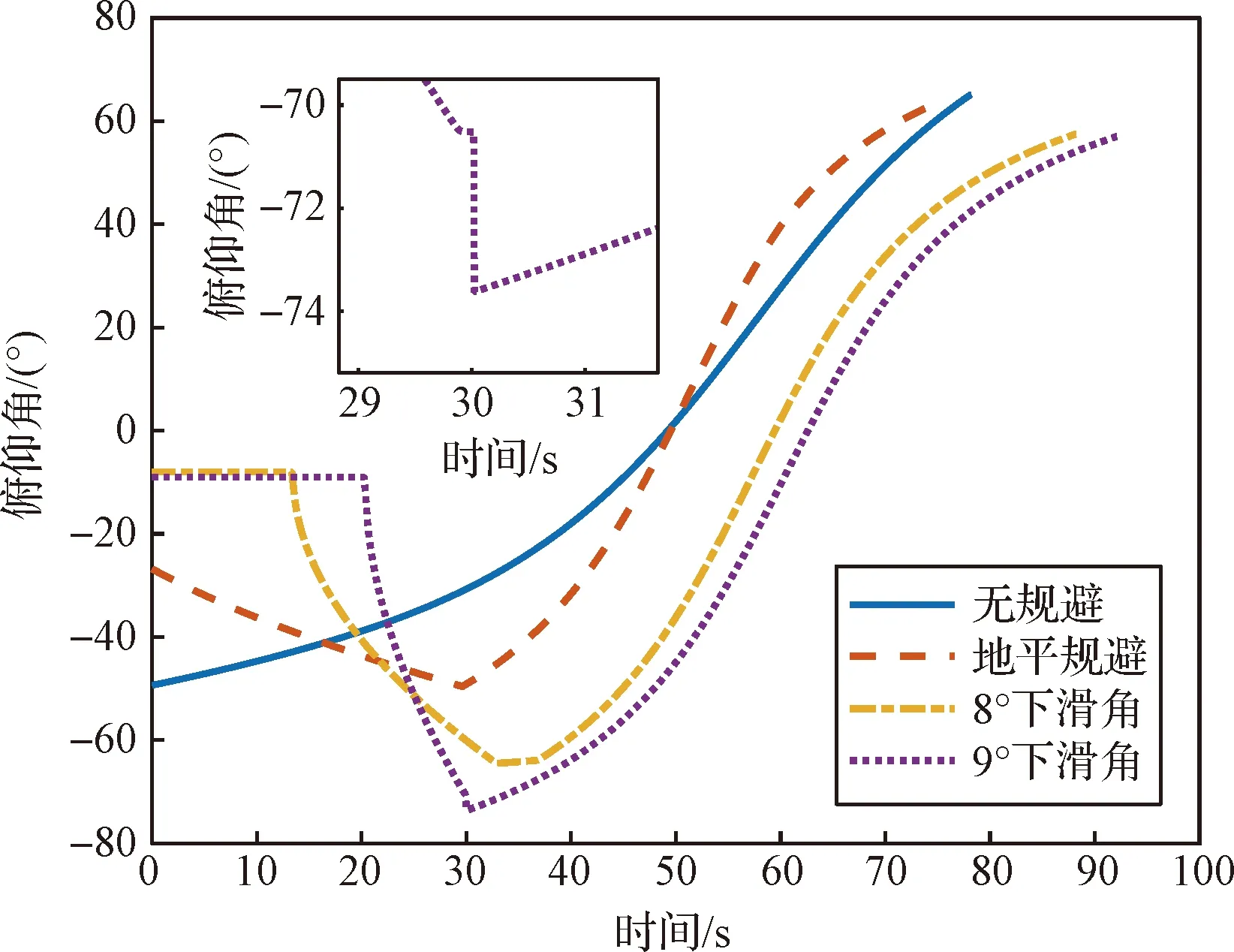
图9 碰撞规避仿真工况的推力俯仰角Fig.9 Thrust pitch angles of collision avoidance simulation cases

碰撞规避仿真工况的制导时长和推进剂消耗见表3。从中可知,有地平规避与无碰撞规避相比制导时长减少3.2 s推进剂消耗增加6.5 kg,有8°下滑角约束与无碰撞规避相比制导时长增加0.7 s推进剂消耗增加18.3 kg,有9°下滑角约束与无碰撞规避相比制导时长增加13.9 s推进剂消耗增加75.6 kg。本节仿真结果说明新制导方法的碰撞规避策略有效,并且满足碰撞规避要求后付出的推进剂代价相对小。

表3 碰撞规避仿真工况的制导时长和推进剂消耗Table 3 Time-to-go and fuel consumptions of collision avoidance simulation cases

4.3 有终端加速度约束

设计有终端加速度约束仿真工况来验证3.3节中方法,初始速度取为[0, 0, -75]Tm/s,目标终端加速度为[0, 0, 0]Tm/s2。姿态机动最大角速度和最大推力变化率取值见表4。预测校正迭代计算的终止条件为终端位置偏差小于1 m,速度偏差小于0.1 m/s。

表4 有终端加速度约束仿真工况的最大角速度和最大推力变化率Table 4 Maximum angular rate and maximum thrust change rate of terminal acceleration constrained simulation cases

有终端加速度约束仿真工况的轨迹见图10,从中可知,着陆前中期3条轨迹基本重合,着陆后期3条轨迹略有差异,终端时刻3条轨迹都满足了终端位置约束。有终端加速度约束仿真工况的推力比见图11,以工况1为例,前40.2 s为最优反馈制导,之后为匀速转动制导,推力比从0.95降至0.47。有终端加速度约束仿真工况的俯仰角见图12,以工况1为例,在40.2 s处可以清楚的看到俯仰角发生转折,这是因为制导律切换为了匀速转动制导,俯仰角迅速从54.7°转动到0°。推力比和俯仰角的仿真结果表明制导终端状态满足了终端加速度约束。

图10 有终端加速度约束仿真工况的轨迹Fig.10 Trajectories of terminal acceleration constrained simulation cases

图11 有终端加速度约束仿真工况的推力比Fig.11 Thrust throttles of terminal acceleration constrained simulation cases

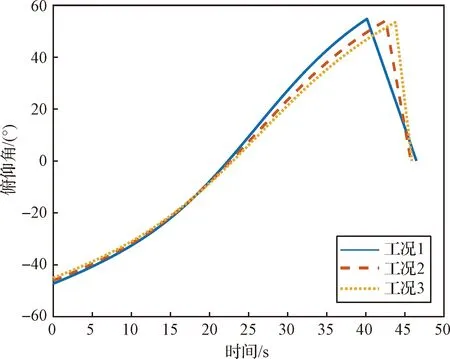
图12 有终端加速度约束仿真工况的俯仰角Fig.12 Thrust pitch angles of terminal acceleration constrained simulation cases

有终端加速度约束仿真工况的数值结果见表5。从表中可知,虽然匀速转动制导时长随着最大角速度和最大推力变化率增大而减小,但是总制导时长并没有出现等幅度变化,而是变化很小。匀速转动制导时长越短则推进剂消耗越少。工况1的推进剂消耗最多,与4.1节中无终端加速度约束工况相比仅增加了6.3 kg,相对增量为2.7%。工况1到3的预测校正迭代次数依次减少,说明匀速转动制导允许的最大角速度和最大推力变化率越大,则预测校正需要的迭代次数越少。以上结果表明最优反馈制导和匀速转动制导的组合使用方法有效,使得着陆终端既满足了位置速度约束,又满足了加速度约束。

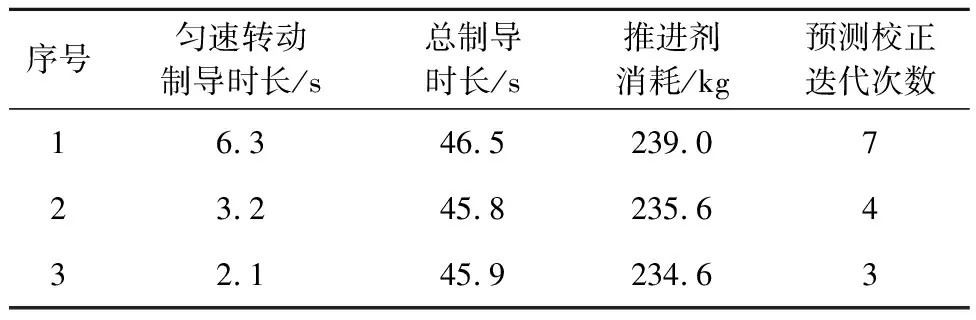
表5 有终端加速度约束仿真工况的制导时长和推进剂消耗Table 5 Time-to-go and fuel consumption of terminal acceleration constrained simulation cases

5 结 论

针对行星定点着陆动力下降段制导问题,从工程实际出发,考虑推力范围受限、连续变推力、碰撞规避和终端加速度共4方面约束,对传统的最优反馈制导方法进行改进和完善。首先,提出推力范围受限且连续变推力约束下的最优反馈制导的制导时长高效寻优方法,经1到2次预测校正即可获得推进剂消耗量接近遍历法的结果,推力剖面为大小大形式。其次,提出基于碰撞规避时长和推力优化分配律的碰撞规避方法,结合坐标系旋转可满足下滑角约束,在连续变推力前提下显著提高碰撞规避能力和着陆点可见性,着陆全程高度单调下降,碰撞规避控制结束后的纵向平面轨迹为直线。最后,提出匀速转动制导和基于预测校正的组合制导参数规划方法,连续衔接最优反馈制导和匀速转动制导,充分发挥推力调节能力,使得终端状态扩充满足加速度约束。新制导方法改进原理清晰,多约束适应性强,虽然使用了数值积分预报,但是总体还属于解析制导方法,计算量显著低于凸优化等数值优化方法和人工智能方法,适合工程应用于行星定点着陆任务中。