(AlxGa1-x)2O3结构、电子和光学性质的第一性原理研究

高 妍,董海涛,张小可,冯文然

(北京石油化工学院新材料与化工学院,北京 102617)

0 引 言

Ga2O3存在α相、β相、γ相、δ相和ε相5种不同结构,其中β-Ga2O3是最稳定的一种,其他相在特定条件下均会转变为β相。β-Ga2O3的带隙值为4.8 eV,其在超宽带隙应用中具有很大的潜力[1],例如,可应用于太阳能器件[2]、钝化涂层[3]、深紫外(deep ultraviolet, DUV)光电探测器(photoelectric detector, PD)[4]和DUV透明电极[5]等。尽管β-Ga2O3的截止波长在紫外波段内,但继续缩短其在DUV光谱区域的截止波长仍具有挑战性[6]。为进一步增大β-Ga2O3薄膜的带隙宽度,研究人员开展了大量的工作。目前已经证明,Al掺杂对增加β-Ga2O3的带隙宽度具有显著的效果。由于Al和Ga的电子结构相似,同时Al2O3具有极宽的带隙(块状Al2O3为～8.8 eV,非晶态Al2O3薄膜为～6.4 eV),因此,改变Al掺杂浓度可以使(AlxGa1-x)2O3的带隙增大到4.8～8.7 eV[7]。

迄今为止,科研人员已经通过各种沉积技术成功制备了(AlxGa1-x)2O3薄膜,包括脉冲激光沉积[8](pulsed laser deposition, PLD)、化学气相沉积[9](chemical vapor deposition, CVD)、磁控溅射[10]和分子束外延[11](molecular beam epitaxy, MBE)等。此外,在探索(AlxGa1-x)2O3薄膜的工艺参数方面也取得了突破性进展。Wang等[12]采用PLD在400 ℃的衬底温度下制备了具有高透射率的优质(AlxGa1-x)2O3薄膜。最近,Chen等[6]证明,在33%的O2浓度(CO2=[O2]/[O2+Ar]×100%)条件下,退火后的氧化铝镓薄膜的光学带隙扩大到4.97 eV。然而,除上述33%的CO2外,(AlxGa1-x)2O3薄膜在16%的CO2下实现了最佳的光电器件性能。他们将这种带隙宽度和器件性能的不一致归因于晶体质量。研究结果表明,溅射条件会显著影响(AlxGa1-x)2O3薄膜基光电探测器件的性能。Zhang等[13]研究发现,改变Al含量,可对PLD沉积(AlxGa1-x)2O3薄膜的带隙宽度进行调制。近年来,尽管(AlxGa1-x)2O3薄膜的制备工艺更加简化,成本也大幅度降低,但其理论研究,尤其是在电子结构层面的研究还远远不够。2017年,Ma等[14]通过第一性原理计算研究了本征缺陷对(AlxGa1-x)2O3电子和光学性质的影响。遗憾的是,该工作并未涉及Al浓度对结构和性能的影响研究,而Al掺杂浓度对于探究β-Ga2O3带隙变化原理至关重要。最近,Mondal等[15]从理论上确定了Ca掺杂α-Ga2O3的微弱p型电导率,为克服制备p型Ga2O3所面临的困难提供了新思路。然而,关于Al浓度与(AlxGa1-x)2O3性质之间的关系,尚缺乏深入研究。2014年,郑树文等[16]采用第一性原理方法分析了Al掺杂对β-Ga2O3电子结构和能带的影响,发现计算结果与实验结果偏差较大。张振东[17]也对Al掺杂β-Ga2O3的光学性质进行了分析,然而由于掺杂量的局限性,对实验研究的指导意义不大。因此,本文采用第一性原理计算,对Al掺杂β-Ga2O3体系进行系统研究,从理论上分析Al掺杂浓度对(AlxGa1-x)2O3三元合金的电子结构和光学性能影响,为该体系今后的实验研究提供完备的理论依据。

1 模型与计算方法

本研究中所有的几何结构优化和计算均基于密度泛函理论(density functional theory, DFT),并采用Materials Studio软件的CASTEP模块进行[18]。本文采用广义梯度近似(generalized gradient approximation, GGA)中的Perdew-Burke-Ernzerhof (PBE)泛函来处理交换关联能,选择超软赝势[19]来描述离子与价电子之间的相互作用。基于C2/m空间群,构建了1×2×2的β-Ga2O3超胞,其中包括32个Ga原子和48个O原子,如图1所示。Ga(1)和Ga(2)分别代表两个不同的Ga原子位置,同时,O原子也有三个不同的位置,分别用O(1)、O(2)和O(3)表示。对比Al原子分别取代两种不同位置Ga原子的生成能,发现八面体的Ga(2)是比四面体的Ga(1)更加稳定的Al原子取代位置。因此,本团队用Al原子替换晶胞中一个Ga(2)原子来构建(AlxGa1-x)2O3模型,如图1(b)所示。需要说明的是,由于两种取代方式总能量相差很小,当Al掺杂浓度较大时,也采用Ga(1)位置取代的方式。从而得到(AlxGa1-x)2O3三元合金,x分别取值0、0.25、0.50和0.75。

图1 1×2×2超胞的晶体结构Fig.1 Crystal structure of 1×2 ×2 supercells

为获得高精度的计算结果,本文所用平面波截止能量为380 eV,在所有布里渊区都采用了1×2×1的Monkhorst-Packk点网格密度。并使用Broyden-Fletcher-Goldfarb-Shanno (BFGS)方法对模型进行了几何优化。Ga、O和Al的价电子构型分别为3d104s24p1、2s22p4和3s23p1,能量收敛为1×10-5eV/atom,力容差为0.3 eV/nm,最大位移为0.000 1 nm,最大应力为0.05 GPa。根据优化后的模型结构,计算并分析了(AlxGa1-x)2O3合金的结构、电子结构特性和光学性质。

2 结果与讨论

2.1 (AlxGa1-x)2O3三元合金结构优化

为保证模型和计算方法的合理性,首先对本征β-Ga2O3和(AlxGa1-x)2O3的结构进行了优化计算。表1给出了GGA-PBE函数计算出的晶格常数、晶胞体积和角度。对于本征β-Ga2O3结构,晶格常数为a=1.250 2 nm、b=0.309 2 nm、c=0.590 1 nm、β=103.710°,这与文献报道的理论值一致[20]。由于Al3+的离子半径(0.054 nm)小于Ga3+的离子半径(0.062 nm),当Ga原子被Al原子取代时,晶胞体积会减小,这就导致了β-Ga2O3的晶格常数和体积随Al掺杂浓度的增加而逐渐减小。

表1 本征β-Ga2O3和(AlxGa1-x)2O3的晶格常数Table 1 Lattice parameters of intrinsic β-Ga2O3 and (AlxGa1-x)2O3

本征β-Ga2O3和(AlxGa1-x)2O3的键长计算结果如表2所示。显然,(AlxGa1-x)2O3中Ga—O键的键长小于O—O键和Al—O键的键长。这可能是由于与Ga原子相比,Al的原子半径更小。同时,Ga—O键、O—O键和Al—O键的键长随Al浓度的增加而逐渐减小。

表2 本征β-Ga2O3和(AlxGa1-x)2O3的键长Table 2 Bond lengths of intrinsic β-Ga2O3 and (AlxGa1-x)2O3

2.2 (AlxGa1-x)2O3合金电子电荷密度分析

β-Ga2O3的键合类型问题一直颇受争议,因其与传输特性息息相关[21-22],故本文将进行深入探究。为确定晶体的键合特征,本文分析了本征β-Ga2O3和(Al0.25Ga0.75)2O3合金的电荷密度分布情况。可以看出,本征β-Ga2O3具有较强的共价键特征,如图2(a)所示。与Ga原子相比,Al的价电子相对较少,因此通过图2(b)可以观察到:与本征β-Ga2O3中Ga和O原子之间的电子密度相比,(Al0.25Ga0.75)2O3合金中Al原子和O原子之间的电子密度有所降低。

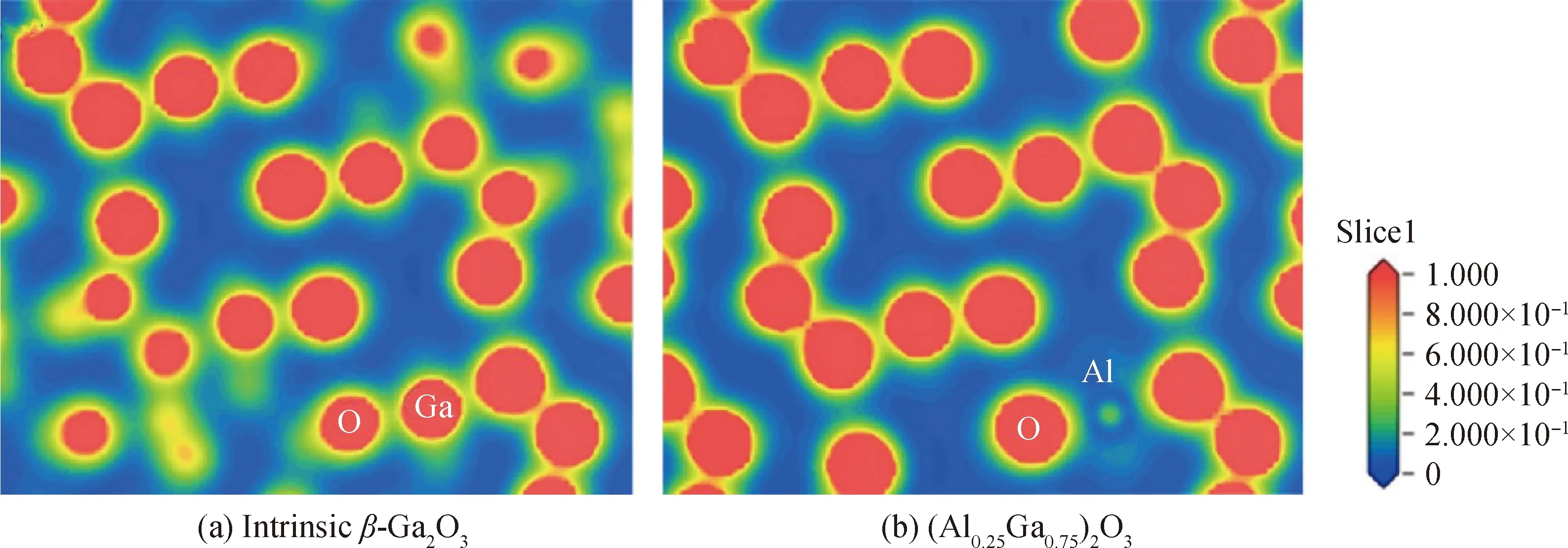
图2 Al掺杂前后电子密度分布图Fig.2 Electron density distribution images before and after Al doping

2.3 (AlxGa1-x)2O3合金能带结构分析

图3为本征β-Ga2O3在布里渊区的能带结构图,图中所示的能量零点即为费米能级。结果表明,经GGA-PBE函数计算得到的本征β-Ga2O3带隙为1.934 eV,远远小于实验结果值4.9 eV[23]。这是由DFT算法被严重低估造成的,为了弥补DFT算法的局限性[24],在计算过程中应引入剪刀算符[25]或采用GGA+U算法[26]。与GGA+U算法相比,剪刀算符更加方便直接,并且引入剪刀算符能够改变所有导电能级以匹配实验所测的带隙值[27]。在本文中,将剪刀算符值设为2.868 eV。

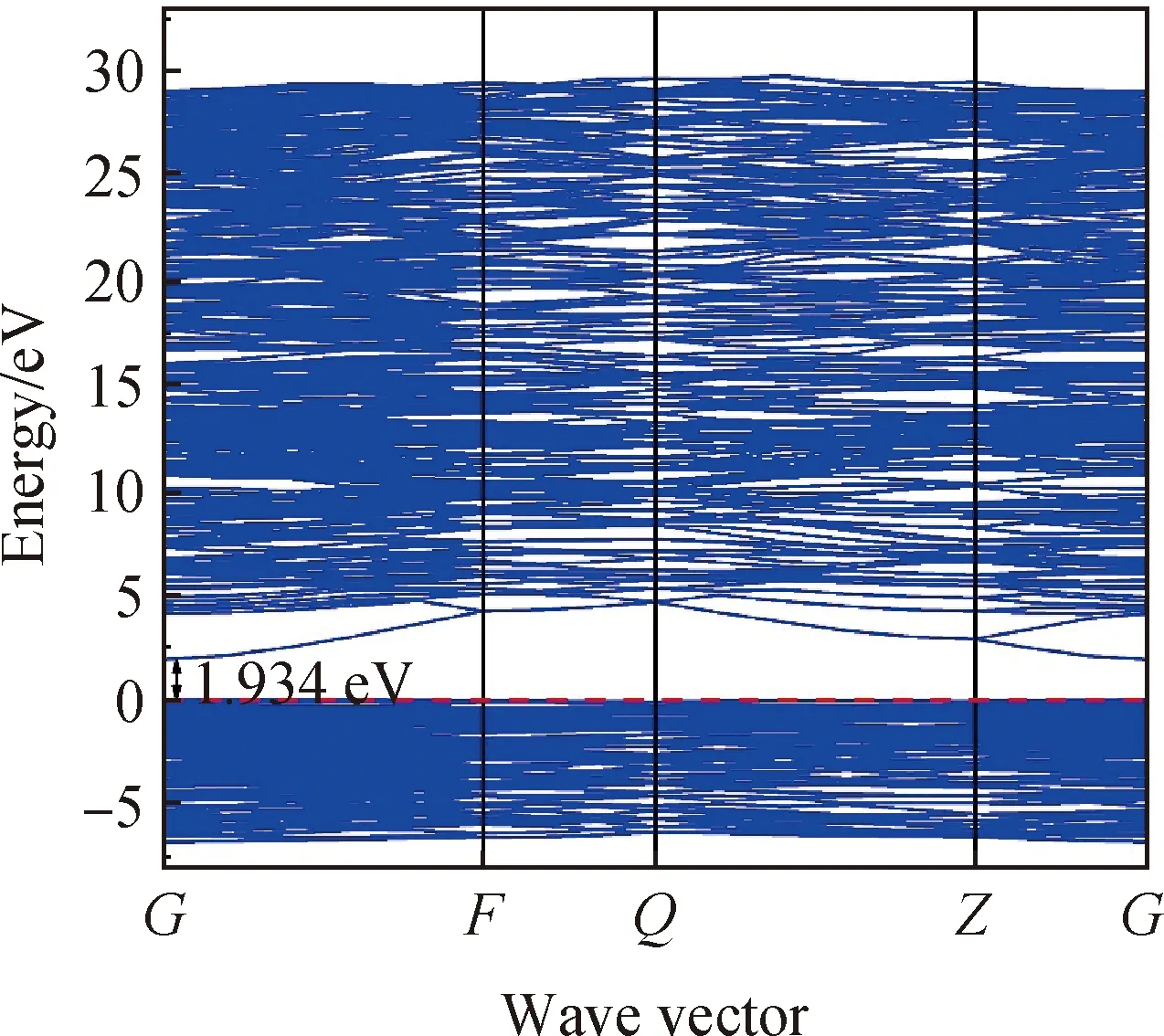
图3 无剪刀算符时本征β-Ga2O3的能带结构Fig.3 Band structure of intrinsic β-Ga2O3 without scissor operator

图4为用剪刀算符计算出的本征β-Ga2O3和(AlxGa1-x)2O3的能带结构图。由图可知,经过剪刀算符校正后,本征β-Ga2O3的带隙为4.802 eV,与实验结果较为吻合[28]。价带顶和导带底均位于G点,表明β-Ga2O3具有直接带隙的性质,这意味着价带中的电子跃迁不受声子的影响。(AlxGa1-x)2O3的能带结构表现出更平滑的价带结构,说明本征β-Ga2O3的空穴有效质量较大,因此空穴迁移率较低[15]。如图4(b)～(d)所示,当掺杂Al原子后,可以观察到直接带隙的宽度显著增大(5.203～6.380 eV),并且随着Al浓度的增加,带隙继续增大。

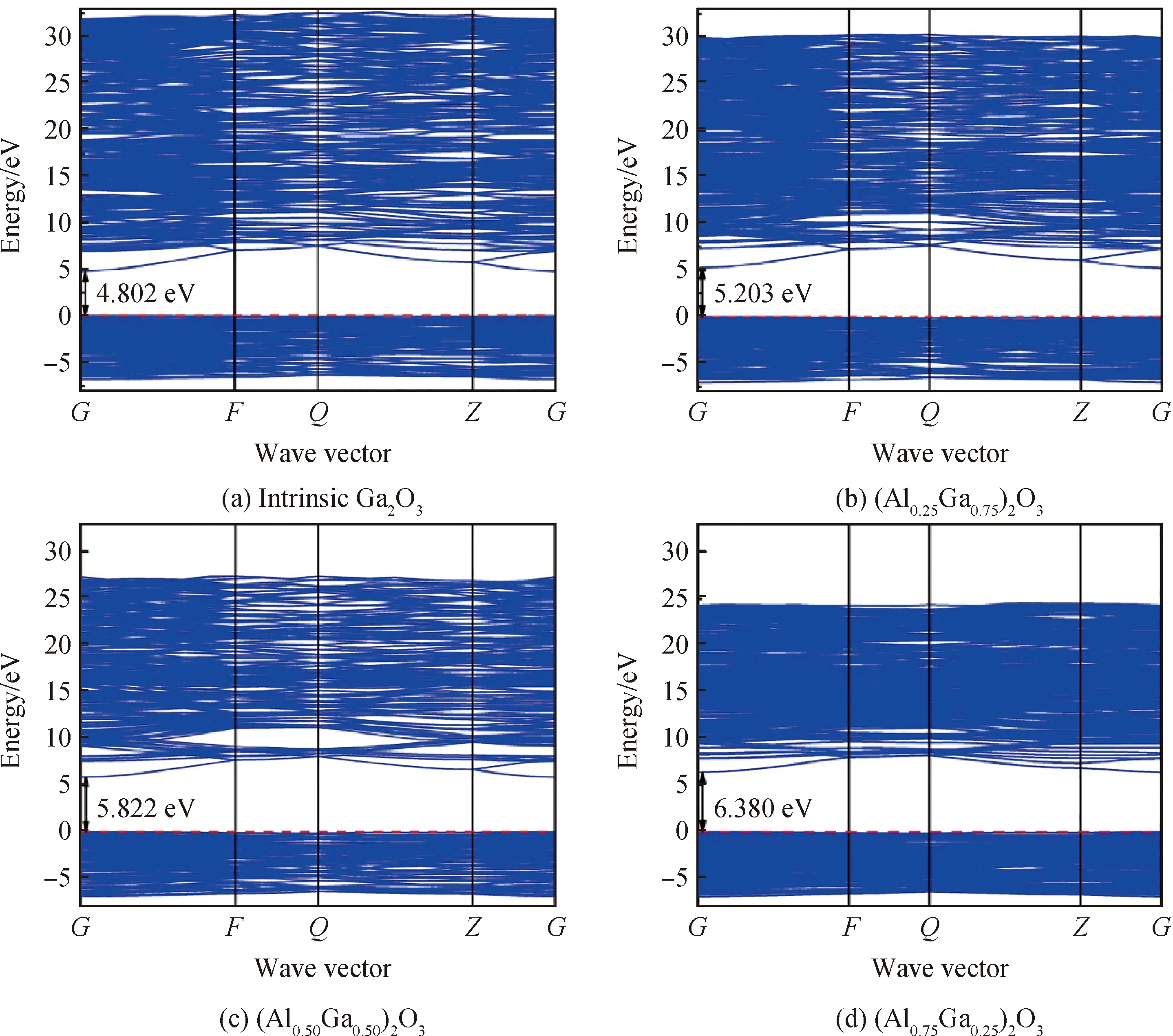
图4 有剪刀算符时本征β-Ga2O3和(AlxGa1-x)2O3的能带结构Fig.4 Band structures of intrinsic β-Ga2O3 and (AlxGa1-x)2O3 with scissor operator

2.4 (AlxGa1-x)2O3合金态密度分析

为研究不同态电子轨道对(AlxGa1-x)2O3体系能带的贡献,计算了(AlxGa1-x)2O3体系的总态密度和分态密度,计算结果如图5所示。可以看出,在不同Al掺杂浓度条件下,(AlxGa1-x)2O3体系的价带顶都由Ga 4s、Ga 4p和O 2p轨道组成。而对于本征β-Ga2O3,Ga 4s和Ga 4p轨道电子均对导带底有重要贡献。(AlxGa1-x)2O3的导带底主要由Ga 4s轨道构成,Al 3s和Al 3p轨道对导带底也有一定的贡献。这种能带结构特征也同样决定了(AlxGa1-x)2O3的物理性质,包括导带底的电子质量。由此可见,β-Ga2O3的带隙受价带顶中的O 2p轨道和导带底中的Ga 4s轨道电子的共同影响。可以清楚地观察到,掺杂Al后,态密度向高能侧偏移了近3 eV,如图5(c)、(d)所示,从而导致带隙增大,这与图4中的能带结果一致。同时,在费米能级以上约16 eV处出现了Al 3p轨道的特征峰。在价带和导带上,Al 3s和Al 3p态与O 2s和O 2p态均重叠,这表明Al原子和O原子之间存在共价键。

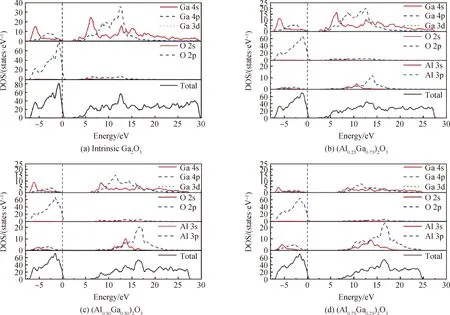
图5 本征β-Ga2O3和(AlxGa1-x)2O3的态密度图Fig.5 Density of states of intrinsic β-Ga2O3 and (AlxGa1-x)2O3

2.5 (AlxGa1-x)2O3合金介电函数虚部分析

式(1)所示的介电函数是研究体系光学性质的关键。

ε(ω)=ε1(ω)+iε2(ω)

(1)

式中:ε1(ω)和ε2(ω)分别表示介电函数的实部和虚部。介电函数实部ε1(ω)与材料吸收系数描述的介电能量损失或光吸收有关。虚部ε2(ω)对应于电介质中存储的能量。通常,计算复合介电函数虚部ε2(ω)是对占用和未占用的电子状态之间的跃迁进行求和,如公式(2)所示。

(2)

式中:ω是入射光子的频率,e是电子电荷,m是电子有效质量,M是偶极矩阵列,i和j分别表示初始状态和最终状态,fi表示第i态费米分布函数,Ei为第i态电子能量,k为波矢。实部ε1可以根据式(3)的Kramers-Kronig变换方程从虚部ε2推导出来。

(3)

式中:P是积分的主值,ω′为最大入射光子频率。图6所示为本征β-Ga2O3和不同x取值(AlxGa1-x)2O3的介电函数虚部。由此可见,在0～50 eV的能量范围内,其主要峰位于10～20 eV,对应从O 2p态到Ga 4s态的价带跃迁。相对而言,(AlxGa1-x)2O3体系的峰值较弱。此外,(AlxGa1-x)2O3体系的介电函数虚部发生显著蓝移。并且,随着Al掺杂浓度的增加,蓝移现象加剧。

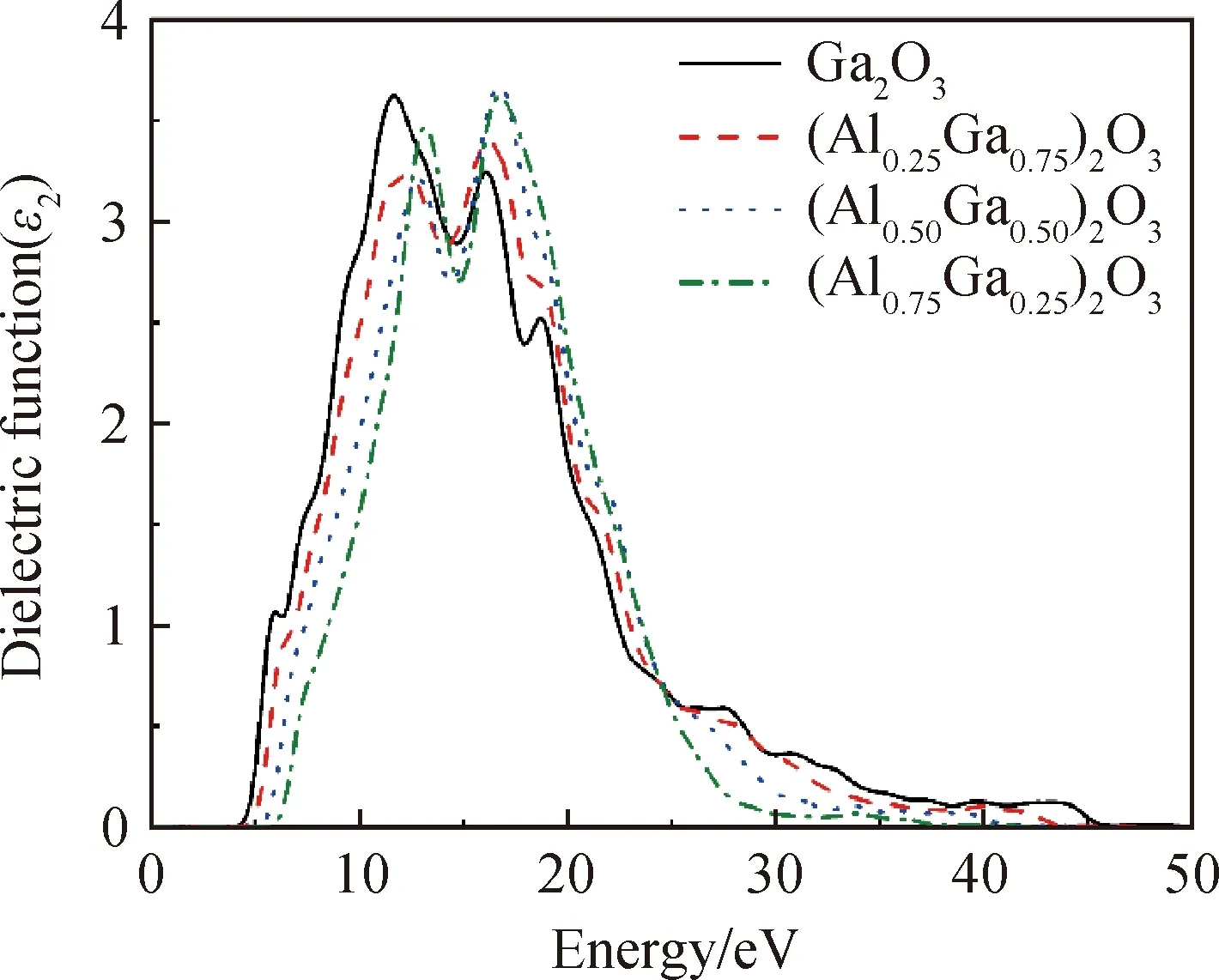
图6 本征β-Ga2O3和不同x取值(AlxGa1-x)2O3的介电函数虚部Fig.6 Imaginary part of dielectric function of intrinsic β-Ga2O3 and (AlxGa1-x)2O3 with different x values

2.6 (AlxGa1-x)2O3合金光学性质分析

根据介电函数,吸收系数α可由式(4)推导

(4)

本征β-Ga2O3和不同x取值(AlxGa1-x)2O3体系的吸收光谱如图7所示。本征β-Ga2O3的吸收边位于4.8 eV,与其带隙值一致。这种本征吸收是由价带顶中的O 2p态和导带底中的Ga 4s态之间的跃迁产生的,而(AlxGa1-x)2O3的吸收边随带隙改变而变化。此外,随着Al掺杂浓度的增加,吸收系数发生蓝移。

图7 本征β-Ga2O3和不同x取值(AlxGa1-x)2O3的吸收光谱Fig.7 Absorption spectra of intrinsic β-Ga2O3 and (AlxGa1-x)2O3 with different x values

3 结 论

本文采用基于DFT的第一性原理计算,研究了不同Al掺杂浓度(即x值)对(AlxGa1-x)2O3体系晶体结构、电子性能和光学性质的影响。结果表明,Al掺杂后,晶格常数降低,Ga—O、O—O和Al—O键的键长随晶格常数的变化有类似的趋势。态密度分析结果表明,(AlxGa1-x)2O3合金的带隙由价带顶的O 2p和导带底的Ga 4s轨道确定。本征β-Ga2O3的带隙计算结果约为4.802 eV,Al掺杂后带隙增大到5.203～6.380 eV。同时,研究发现掺杂结构中介电函数的虚部和吸收系数均发生了显著的蓝移现象。并且,随着Al掺杂浓度的增加,蓝移现象加剧。