水下航行器对接过程下的动力学建模与运动仿真研究

周 超，张 伟，李德军，王 璇，杨申申，王小庆

（1.中国人民解放军92228部队，北京 100072；2.中国船舶科学研究中心，深海载人装备国家重点实验室，江苏 无锡 214082；3.深海技术科学太湖实验室，江苏 无锡 214082）

0 引 言

水下航行器作为一种海洋探测装备，其体积小、隐身性好、机动性强、成本低、可快速组网，探测能力强，可广泛用于海底科学考察、水域勘察与识别、海洋生物群落调查、水下线缆维修和海底打捞等。水下航行器在长时间航行作业时，续航能力直接影响水下航行器探测能力，需要搭载在母艇上，以补充能量或者交换数据[1]。

世界范围内开展水下无人航行器研发的国家主要为美、俄、欧亚等国，其中，美国在水下无人航行器技术领域始终处于领先地位。目前,许多强国重视无人航行器与水下平台的搭载。例如，瑞典的SAABSUBROV 航行器，可由潜艇进行操控；美国的“曼塔”（Manta）UUV、俄罗斯的“波塞冬”UUV 都计划搭载于潜艇，辅助潜艇执行水下作战任务；美国新建第三批“弗吉尼亚”级核潜艇也采用了新型艇首结构，为多个无人潜水器的搭载提供了平台基础[2]。

在近距离对接过程中，水下航行器和母平台间存在复杂的水动力干扰。由于水下航行器相对于平台尺寸较小，其航行姿态受影响较大，给对接回收带来了困难。在对接过程中，需要对水下航行器进行不断控制，以抵消水动力干扰，保证对接的精准完成。为了有效控制水下航行器，需要弄清对接过程中的水动力干扰作用机理与规律，为实现对接提供技术支撑。在水下航行器对接水动力干扰研究方面，文献[3]基于CFD技术,研究了潜艇布放回收UUV过程中的相关参数对流场和水动力性能的影响。文献[4]采用CFD技术，计算了大型水下搭载平台与微小型水下机器人间的水动力干扰性能，分析了在不同来流速度和不同间距比时的微小型水下机器人的阻力、升力和倾覆力矩性能，此外,对微小型水下机器人的中纵剖面的压力和速度分布进行了细致的分析。文献[5]采用CFD 技术，采用有限体积法和非结构动网格技术,对AUV 对接过程在不同雷诺数下和不同攻角下的非定场流场进行了模拟研究。

水下航行器对接过程主要分为两步：当水下航行器距离目标平台距离较远时，根据低频声纳的信号，确定目标平台的相对位置和方位，通过远程导引，航行靠近目标平台，并到达平台的垂直面后上方；当水下航行器距离目标平台距离较近时，根据高频声纳或者光学导引方式，开启自动控制功能，完成水下航行器与平台的对接。其中，近距离双体干扰下的对接建模与控制是研究的难点。

本文采用CFD 数值计算，利用RANS 方法求解湍流方程，研究干扰水动力特性及规律，完成水下航行器和母平台不同距离下的水动力干扰计算，进而建立水下航行器对接时的动力学模型。在此基础上，针对不同航速和不同距离下的对接工况，开展干扰水动力对姿态和速度影响的仿真研究；选择干扰影响最大的工况，开展对接运动控制研究，基于动力学模型，采用PID 和滑模控制方法，完成对接控制器设计，开展对接运动仿真。

1 水下航行器运动学

1.1 运动坐标系

为研究小型水下航行器对接时的运动特性，首先应定义O-XYZ为大地坐标系，其固定于地球；定义o1-x1y1z1为水下航行器坐标系，坐标原点为水下航行器的重心；定义o2-x2y2z2为平台坐标系，坐标原点为母平台的重心（如图1所示）。水下航行器相对母平台尺寸较小，其运动受干扰水动力影响较大，而母平台受干扰水动力影响可以忽略，因此本文主要研究对接过程下的水下航行器运动建模问题。

图1 对接空间坐标系Fig.1 Spatial coordinate system under docking

1.2 运动学模型

水下航行器随体坐标系与惯性系转移矩阵[6]为

水下航行器速度关系为

水下航行器角速度关系为

其中，

上式中，X、Y、Z为水下航行器位置，u、v、w为线速度，p、q、r为角速度，φ、θ、ψ为姿态角。

2 水下航行器对接动力学模型

2.1 对接干扰力模型

当水下航行器间进行对接作业时，两者存在相互干扰的水动力。本文采用商业软件STARCCM+，选用SSTk-ω模型进行数值计算分析，该模型的适用性在文献[7]中得到了验证，表明其在近壁面流动分离以及尾流场特性的数值预报上具有较好的适用性。

目前通常采用三维不可压缩粘性Navier-Stokes（N-S）方程作为流体运动的控制方程，求解水下运载平台周围的流场流动，其表达式为

式中，u是流体速度矢量，μ是流体动力粘性系数，p是压力，ρ为流体密度。

首先，开展数值方法的验证工作，选择风洞模型试验结果与计算结果进行比对，不同攻角的水下航行器流体动力系数计算结果和模型试验结果如图2所示。

图2 数值方法验证结果Fig.2 Validation results of numerical method

从图中可以看出，本文计算结果与模型试验结果吻合较好，相关水动力系数值最大偏差为5.65%，证明了计算方法的有效性。

本文以Suboff为对接母平台，选取长方体作为计算域（见图3）。计算域的长度为Suboff 艇长的6倍，其中前方的面距离Suboff首部1.5倍艇长，后方的面距离潜艇尾部3.5 倍艇长，侧向的四个面距离Suboff中心均2倍艇长，假定Suboff航速为3.5 kn。

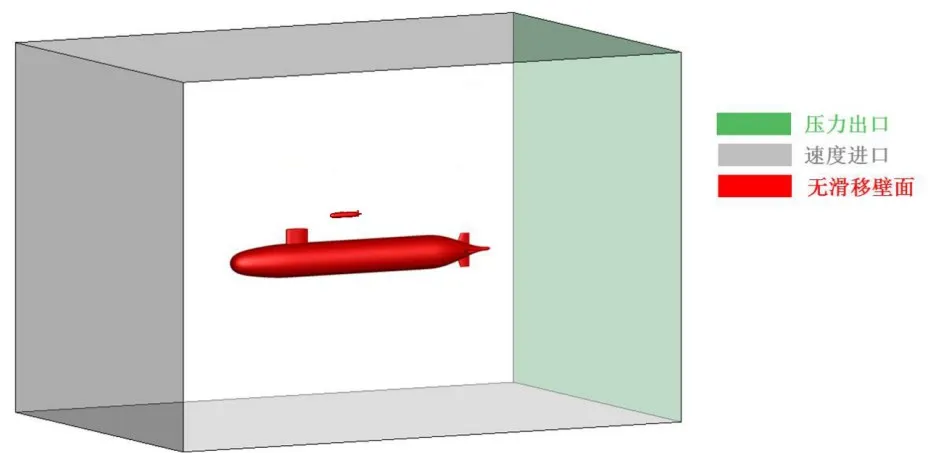
图3 计算域边界条件设定Fig.3 Boundary condition setting in calculation domain

对于整个计算域采用多面体网格、棱柱层网格以及表面重构这三者相结合的方法进行网格的生成。Lx为水下航行器与Suboff 围壳后缘之间的水平距离，h为水下航行器与Suboff 甲板之间的垂向距离，α表示速度攻角，Lw表示平行中体长度，选取对接纵向位置Lx=Lw。分别对水下航行器相距母平台不同距离、不同攻角下的水动力特性进行了预报（典型流动图像见图4）。

图4 水下航行器对接CFD计算流场图Fig.4 CFD calculation flow field diagram of underwater vehicle docking

水下航行器的近距离对接过程在母平台的垂直面上方完成，干扰水动力系数和对接距离的关系如图5～8所示，通过分段函数拟合可得到对接干扰力模型。其中，X’、Z’和M’分别为水下航行器纵向力、垂向力和俯仰力矩系数。表1是对接距离为3.5L和无界下的纵向水动力系数。由表1和图6～8可得到结论：在h≥3.5L时，水下航行器的水动力系数和无平台干扰下的水动力系数几乎一致，水动力几乎没有干扰影响，可视为无界环境。

表1 距离h=3.5L和无界下的X’水动力系数（×10-3）Tab.1 Hydrodynamic coefficients of X’at a distance of h=3.5L and unbounded（×10-3）

图5 无界下的水动力系数（没有干扰下）Fig.5 Hydrodynamic coefficients under unbounded conditions

图6 干扰水动力系数dX’和对接距离的关系曲线Fig.6 Relationship between interference hydrodynamic coefficient dX’and docking distance

图7 干扰水动力系数dZ’和对接距离的关系曲线Fig.7 Relationship between interference hydrodynamic coefficient dZ’and docking distance

图8 干扰水动力系数dM’和对接距离的关系曲线Fig.8 Relationship between interference hydrodynamic coefficient dM’and docking distance

计算结果表明：（1）在h≥3.5L时，可视为无界环境，在无界环境下，随着攻角增大，纵向力几乎无变化，垂向力和攻角呈负相关关系，纵向力矩和攻角呈正相关关系；（2）在对接过程中，水下航行器的纵向力随着对接距离的减小呈现逐渐增加的趋势，攻角在α≤4°范围内，对接距离对纵向力系数影响不大，且在0°攻角时达到最小值，也就是说，在0°攻角时，水下航行器的阻力最小；（3）在3.5 kn航速下的对接过程中，垂向力随着攻角的增大呈现逐渐减小的趋势，在0°攻角时垂向力最小；垂向干扰水动力系数随着对接距离的减小先增大后减小，呈现非线性干扰特性；（4）在3.5 kn航速下的对接过程中，俯仰力矩随着攻角的增大呈现逐渐增加的趋势，在0°攻角时俯仰力矩最小；俯仰干扰水动力系数随着距离的减小先增大后减小，呈现非线性干扰特性。

2.2 舵/推进器模型

无人水下航行器所受到的控制力和力矩主要由舵机和推进器产生，舵包括艏升降舵、艉升降舵和艉方向舵，舵力表达式如式（6）所示。

式中，δb为艏升降舵角，δs为艉升降舵舵角，δr为艉方向舵舵角，其他项无量纲水动力系数可参考文献[8]。

在与母艇航行对接过程中，通过主推保持水下航行器航行状态，艏舵控制航行深度变化，艉舵控制航行纵倾变化；在母艇悬停静态对接过程中，通过垂向推进器定深和纵倾控制完成水下对接过程。

2.3 对接动力学模型

水下航行器对接过程的运动方程如下：

式中：水下航行器η1=[X1,Y1,Z1,φ1,θ1,ψ1]T,v1=[u1,v1,w1,p1,q1,r1]T；母平台η2=[X2,Y2,Z2,φ2,θ2,ψ2]T，v2=[u2,v2,w2,p2,q2,r2]T；M1为航行器的惯性矩阵，C1为航行器的科氏力和向心力矩阵，D1为航行器的水动力矩阵，g1为航行器的静力矩阵，τT1为航行器的推进器推力，τδ1为航行器的舵力，F(η1,η2)为航行器与母平台间的干扰水动力。

采用美国海军舰船研究与发展中心（NSRDC）报告中的标准方程，以水下航行器六自由度运动数学模型为基础，考虑航行器和平台间的动力学干扰，得到水下航行器对接过程的动力学模型方程组[9-10]。水下航行器与母平台的对接假设在母平台中纵垂面上进行，纵向、垂向和纵倾方程如下：

纵向方程为

垂向方程式

纵倾方程为

式中：Fi(x,y,z)为对接干扰水动力，与两者距离h有关，例如式Fi(x,y,z)中，拟合项干扰dZ'ww如式（11）所示；水下航行器其它参数可参考文献[11-12]。

3 水下航行器对接仿真研究

3.1 水下航行器对接干扰仿真研究

（1）为研究不同对接距离下干扰水动力对姿态的影响，选取母平台以3.5 kn 航速进行对接，此时水下航行器完成纵向相对位置的跟踪，其航速保持在3.5 kn，当初始对接距离h0=0.25L和h0=0.4L时对应的垂向干扰水动力和纵倾水动力矩较大，对垂向速度和纵倾角影响如图9和图10所示。

图9 不同对接距离下的垂向速度变化Fig.9 Vertical velocity change under different docking distances

图10 不同对接距离下的纵倾角变化Fig.10 Pitch change under different docking distances

仿真结果表明，h0≥3.5L时，水动力干扰影响可忽略，由于上下不对称，导致产生微小垂向速度和纵倾；h0=0.25L时，干扰水动力对垂向速度和纵倾角影响最大，垂向速度达到0.02 m/s，纵倾值将近4°，尤其在航速3.5 kn时对动态对接带来了难度，垂向速度和纵倾变化和干扰水动力相关，在实际对接时需要引起重视。

（2）为研究不同对接航速下干扰水动力对姿态影响，选取初始对接距离为h0=0.25L，水下航行器分别以2.5 kn、3 kn、3.5 kn 航速进行对接时，垂向速度和纵倾角随时间的变化规律如图11 和图12所示。

图11 不同航速下的垂向速度变化Fig.11 Vertical speed change at different speeds

图12 不同航速下的纵倾角变化Fig.12 Pitch change at different speeds

从仿真结果看出，随着航速的增大，干扰水动力对纵倾和垂向速度的影响增大，其中，在3.5 kn航速下，干扰产生的纵倾角小于4°，该纵倾角并不大，反映该水下航行器外形设计和水动力性能优良。在对接中，可进一步通过对接控制实现精准对接。

3.2 水下航行器对接控制仿真研究

对接时，水下航行器航行至对接母平台上方，首先通过纵向位置控制器，完成水下航行器与母平台纵向相对位置的控制，保证水下航行器和母平台的对接纵向相对位置偏差在0.2 m 范围内，然后通过定深和纵倾调节完成与母平台的对接。选择航速3.5 kn时开启自动对接，定深控制采用艏舵，纵倾控制采用艉舵，纵向位置跟踪和纵倾控制采用PID 控制方法，深度控制采用滑模控制方法。对接控制方案如图13所示。

图13 对接控制结构框图Fig.13 Block diagram of docking control structure

将深度误差取为e（t），切换面选择为s（t），定义滑模函数为

在式（12）中，满足Hurwitz条件，取c＞0，并选择指数逼近定律，如式（13）所示。

在对接过程中，纵倾值不大，取Z¨ ≈w˙，θ˙≈q，由此，可得到深度控制器设计滑模控制律，如式（14）所示，为消除抖震影响，在控制中，采用饱和函数sat（s）代替切换函数sgn（s）。

式中各参数表达可参考文献[13]。其中，F为

饱和函数表达式为

从仿真结果（图14～16）可以看出：深度控制方面，水下航行器在28 s时达到了期望深度，在50 s后稳定，滑模控制对水动力干扰的影响具有一定适应性；纵倾控制方面，结合3.1 节仿真结果，考虑纵倾值不大和系统的稳定性两方面因素，采用PID 控制，由于干扰水动力影响，控制过程纵倾角有一定波动，但纵倾角不大，整体变化在θ≤2°范围，最终控制精度达0.5°。

图14 对接控制纵向相对位置值变化Fig.14 Change in longitudinal relative position of docking control

图15 对接控制深度值变化Fig.15 Change of depth of docking control

图16 对接控制纵倾值变化Fig.16 Change of trim value of docking control

4 结 论

本文研究了不同距离下的双体水动力干扰规律，建立了小型水下航行器对接过程的运动模型，研究了干扰水动力对姿态和速度的影响。在此基础上，采用滑模控制方法，完成定深和纵倾控制，并完成了相应的控制仿真计算。研究结果表明：（1）在h≥3.5L时，可视为无界环境，在无界环境下，随着攻角增大，纵向力几乎无变化，垂向力和攻角呈负相关关系，纵向力矩和攻角呈正相关关系；（2）在对接过程中，水下航行器的纵向力随着对接距离的减小呈现逐渐增加的趋势，垂向干扰水动力系数随着距离的减小先增大后减小，俯仰干扰水动力系数随着距离的减小先增大后减小，呈现非线性干扰特性；（3）仿真结果表明，对接时的水动力干扰主要影响航行器的纵倾和垂向速度，对接运动模型具有很强的非线性特点，滑模控制对水下对接运动控制具有很好的适用性。