考虑界面滑移及局部紊流的船用艉轴承润滑特性研究
2023-09-22吕芳蕊张鑫杰饶柱石郑胜尧施俊杰
吕芳蕊,张鑫杰,饶柱石,郑胜尧,施俊杰
(1.河海大学机电工程学院,江苏 常州 213022;2.上海交通大学a.机械系统与振动国家重点实验室;b.振动、冲击、噪声研究所,上海 200240)
0 引 言
船用艉轴承支撑着螺旋桨轴,其润滑特性对船舶推进轴系的动力学性能及可靠性具有重要影响。船用艉轴承具有突出的特点:首先,由于螺旋桨的重力作用,螺旋桨轴易于发生挠曲变形,中国船舶行业标准CB/Z 338-2005 规定,校中后的轴颈倾角不得超过0.35 mrad,然而,较小的轴颈倾角即可对轴承性能产生显著的影响;其次,艉轴承多处于低速重载工况,高偏心率使最小膜厚远小于最大膜厚[1],最小膜厚附近区域通常为层流流态,而其它区域液膜厚度大得多,可能产生局部紊流,影响轴承特性;最后,为减小摩擦延长使用寿命,艉轴承常采用高分子材料作为承载面,而高分子材料表面能较低,润滑剂易在高分子承载面发生界面滑移,影响轴承润滑性能。
轴的挠曲变形及轴颈倾斜的问题得到了一些学者的关注[2-3],如He 等[2]推导了螺旋桨轴挠曲变形的计算方程,详细分析了轴挠曲对船用艉轴承润滑性能的影响,结果表明轴颈挠曲使轴承最小膜厚显著减小,甚至可能发生混合润滑;Litwin等[4]分析了轴颈倾斜对轴承的影响,指出轴颈倾角越大,承载能力越低;Jang和Khonsari[5]考虑轴颈倾斜建立了磨损对发动机轴承影响的评估模型,并指出轴颈倾斜使最大磨损深度增大,且磨损深度随表面粗糙度增大而增大;Lü等[6]提出了轴颈倾斜下轴承等效支点位置的近似计算方法,并指出等效支点位置变化对轴系动力学特性有显著影响。
上述研究均假定润滑剂未在液固界面处发生滑移,然而,文献[7]的研究证实在高剪切工况下润滑剂可能在其与高分子材料的界面处发生滑移。目前针对界面滑移的研究大多采用滑动长度模型或极限剪应力模型[8-11]。其中极限剪应力模型假设液体在固液界面具有极限剪应力,当其剪应力达到该值时则发生界面滑移,该假设被许多研究所证实。Spikes等[12-13]利用极限剪应力模型研究了界面滑移对轴承承载力及摩擦力的影响,其研究结果表明界面滑移降低了流体润滑轴承的承载力和摩擦力;Ma等[14]基于极限剪应力模型,利用多线性有限元法计算了考虑界面滑移的轴承性能,指出可通过合理设计滑移区优化轴承性能;Wang等[15-16]在滑动长度模型的基础上考虑了极限剪应力的影响,推导了考虑界面滑移的广义雷诺方程,并指出界面滑移易发生于间隙小、剪应力大的区域;Cheng等[17]针对空化区的润滑膜提出了速度滑移模型;王占朝等[18]考虑界面滑移建立了带平衡梁结构的水润滑可倾瓦轴承的瞬态模型。上述研究均表明界面滑移会影响轴承性能,然而船用艉轴承中的界面滑移问题尚未得到重视。而Jin 等[7]的试验研究表明润滑油可在高分子材料表面产生滑移,并测得了润滑油在聚四氟乙烯表面的极限剪应力。可见,对于承载面为高分子材料的船用艉轴承,有必要研究界面滑移对轴承性能的影响。
目前针对船用艉轴承的研究通常假设液膜为层流状态。然而,大型艉轴承的高偏心率导致最大膜厚往往远大于最小膜厚,在这类大型艉轴承中可能发生局部紊流。对紊流润滑的研究,以Constantinescu[19-20]、Ng-Pan[21]和Elrod-Ng[22]提出的紊流模型应用最为广泛。Bouard 等[23]分别采用上述三种模型分析了紊流流态对可倾瓦轴承性能的影响,结果表明三种模型所得结果均较为接近;Braunetiere[24]在Elrod-Ng 模型的基础上提出了一种改进的低雷诺数流动模型,并将该模型应用于静压非接触端面密封验证了模型的正确性;Zhu 等[25]的研究结果表明紊流对轴颈倾斜下的粗糙轴承影响不可忽视;张永芳等[26]推导得到了适用于高偏心及重载工况的紊流轴承承载力的近似表达式;Susilowati 等[27]利用三维CFD 方法对不同流态下的轴承性能进行了比较,发现在紊流和层流两种流态下压力具有相同的变化趋势;Mallya 等[28]研究了紊流工况下轴颈倾斜的水润滑轴承的润滑特性,发现相同偏心率下紊流和轴颈倾斜均增大了轴承的承载能力。上述研究假定轴承处于全紊流状态,而大型重载船用艉轴承的最小膜厚较小,其附近区域往往处于层流流态,对于膜厚较大的区域则可能进入紊流流态,有必要针对船用艉轴承中局部紊流的影响开展研究。
综上所述,目前船用艉轴承的轴颈挠曲问题已取得一定研究进展,而船用艉轴承中存在的界面滑移及局部紊流问题尚未得到重视,综合考虑界面滑移、局部紊流、轴颈挠曲等多种因素影响的轴承研究尚未见报道。为研究界面滑移和局部紊流对船用艉轴承润滑特性的影响,本文提出一种考虑界面滑移及紊流的倾斜轴颈轴承润滑模型,并应用该模型分析界面滑移及局部紊流对船用艉轴承性能的影响。
1 考虑紊流及界面滑移的轴承模型
本章首先建立考虑轴颈倾斜的轴承几何模型,然后分析流态转变及界面滑移的影响,建立综合考虑二维界面滑移及紊流的轴承分析模型。
1.1 考虑轴颈倾斜的轴承几何模型
针对径向滑动轴承的研究多假定轴颈与轴承孔的中心线互相平行,但由于工程实际中制造、安装、重力作用等因素,主轴易于挠曲变形,特别是对于船用艉轴承,螺旋桨轴悬伸于船外,螺旋桨的重力作用导致轴发生竖直方向的挠曲变形,进而使轴线与轴承孔中心线在竖直平面内产生夹角γ(如图1(a)所示)。轴承宽度远小于整个轴的长度,因此一般可忽略轴颈在轴承孔中的弯曲变形,近似认为γ在轴向为定值。
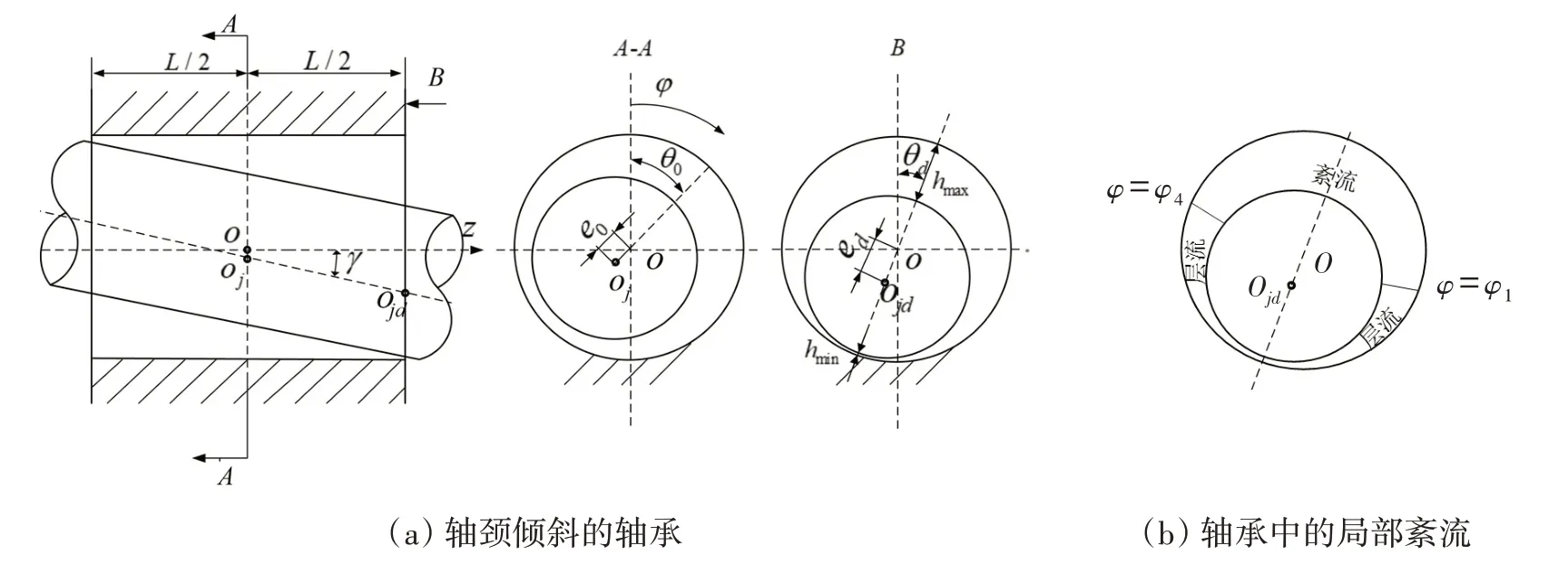
图1 含局部紊流的轴颈倾斜轴承示意图Fig.1 Geometry model of the misaligned journal bearing with local turbulence
轴颈沿竖直方向倾斜时,轴承的液膜厚度[6]可表达为
1.2 考虑界面滑移及紊流的轴承控制方程
船用艉轴承等重载轴承服役时偏心率较大,其最小液膜厚度hmin远小于最大液膜厚度hmax。最小膜厚附近区域通常为层流流态,而在轴承的其它区域特别是在最大膜厚附近的区域,液膜厚得多,因而当地雷诺数较大,进而可能发生局部紊流(如图1(b)所示)。以x=rφ表示周向坐标(r为轴颈半径),以y表示径向坐标,以z表示轴向坐标,将轴颈表面和轴瓦表面在x方向的运动速度分别定义为U1、U2。根据Ng-Pan紊流模型,界面无滑移时x和z方向单位时间内的流量分别为
其中,ReL为当地雷诺数,ReL>Rec时为紊流,ReL≤Rec时为层流,Rec=41.1/为临界雷诺数,ψ为轴承间隙比。TBA、TBB、ETA、ETB为紊流因子,其取值见表1。ReL作为流态判定因子,表达了局部紊流的影响。
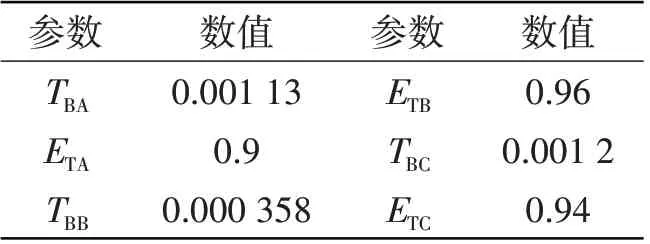
表1 紊流因子Tab.1 Turbulence factors
对于未发生界面滑移的稳态工况径向轴承,U2=W1=W2=0,则考虑紊流的广义雷诺方程为
当流体在表面2 发生相对滑动时,式(2)中的U2应以液膜在表面2 边界处沿x方向的绝对速度U2s替代,类似地,式(3)中W2应以液膜在表面2 边界处沿z方向的绝对速度W2s替代。接下来推导U2s和W2s的控制方程。
如图2(a)所示,液体在两界面间流动,假设其在固液界面处的剪应力达到极限剪应力,则液体在界面处产生滑移。定义τl1、τl2分别为液体在界面1、2 处的极限剪应力,如图2(b)所示,液体在界面2产生滑移时,其剪应力为τ=±τl2,τ在x、z方向的分量为
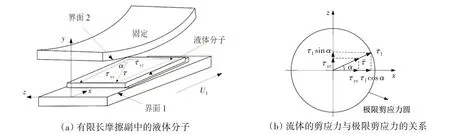
图2 液体在固液界面处的极限剪应力示意图Fig.2 Schematic diagram of limit shear stress of liquid at solid-liquid interface
式中,α=arctan(τyz/τyx)。
根据Ng-Pan紊流模型,不考虑滑移时界面处的剪应力可按下式求解:
式中,正号用于表面2,负号用于表面1。
液体在界面2处滑移时,式(6)中的U2应替换为液体绝对速度U2s,由式(5)和式(6),可得到
W2s则可通过类似的方法求解得到:
将式(7)代入式(2),式(8)代入式(3),再将式(2)与式(3)代入流量平衡方程:
则可得到广义雷诺方程:
上式适用于液膜在界面2处发生滑移的轴承。
若流体在界面1发生滑移,则可推导得到广义雷诺方程为
式(10)和式(11)考虑了界面滑移及紊流的影响,适用于相应的轴承性能分析。
进行数值仿真时,首先根据节点处的液膜厚度、润滑剂运动粘度、轴颈线速度计算当地雷诺数及紊流系数,然后代入雷诺边界条件,即可求解广义雷诺方程(4)、(10)和(11),得到液膜压力分布,轴承承载力可根据下式求解得到:
式中,Fξ、Fη分别为液膜动压力在水平和竖直方向的分力,A为轴承展开面面积。
润滑膜在轴颈表面的剪应力为
轴承摩擦力由下式计算得到:
2 数值求解流程及验证
基于商业软件Matlab 采用有限差分法编制了综合考虑界面滑移、紊流及轴颈倾斜的轴承性能仿真程序,图3为程序计算流程图。首先通过方程(1)计算各节点的液膜厚度,然后通过节点的膜厚、润滑剂运动粘度、轴颈线速度计算当地雷诺数及紊流系数;计算网格节点的剪应力,根据剪应力判断两界面处是否发生界面滑移;根据滑移情况选取各区域应采用的方程,并计入雷诺边界条件和不同边界处的压力、流动连续性条件,求解广义雷诺方程(4)、(10)及(11),即可得到轴承的压力分布,进而可得到轴承润滑特性。本程序中需要考虑轴颈倾斜的影响,因此对整个轴承宽度进行了网格划分。

图3 计算流程图Fig.3 Flow chart of numerical calculation
为验证本文提出的模型,用上述计算程序计算了文献[14]中轴承的性能,并与文献结果进行了对比。文献[14]中轴承参数为:偏心率ε0=0.8,长径比L/D=1,无量纲极限剪应力根据计算结果>6 时液膜不发生界面滑移),文献考虑了界面滑移的影响,流态为层流。定义了与文献中相同的无量纲参数=pψ2/2μΩ,=得到轴承的无量纲压力分布、无量纲承载力及摩擦力如图4 所示,其中图4(a)为液膜压力分布图,可见润滑膜在轴瓦界面产生的滑移,使最大压力、轴承承载力与摩擦力均有所降低;图4(b)为无量纲摩擦力及承载力本文结果与文献结果对比图,可以发现利用本文模型所得计算结果与文献[14]较为吻合,从而可证明该模型在层流润滑分析中的正确性。层流流态是本文模型的一种特例,由于该算例未发生紊流,因此后续需通过试验进一步验证该模型在紊流流态下的正确性。
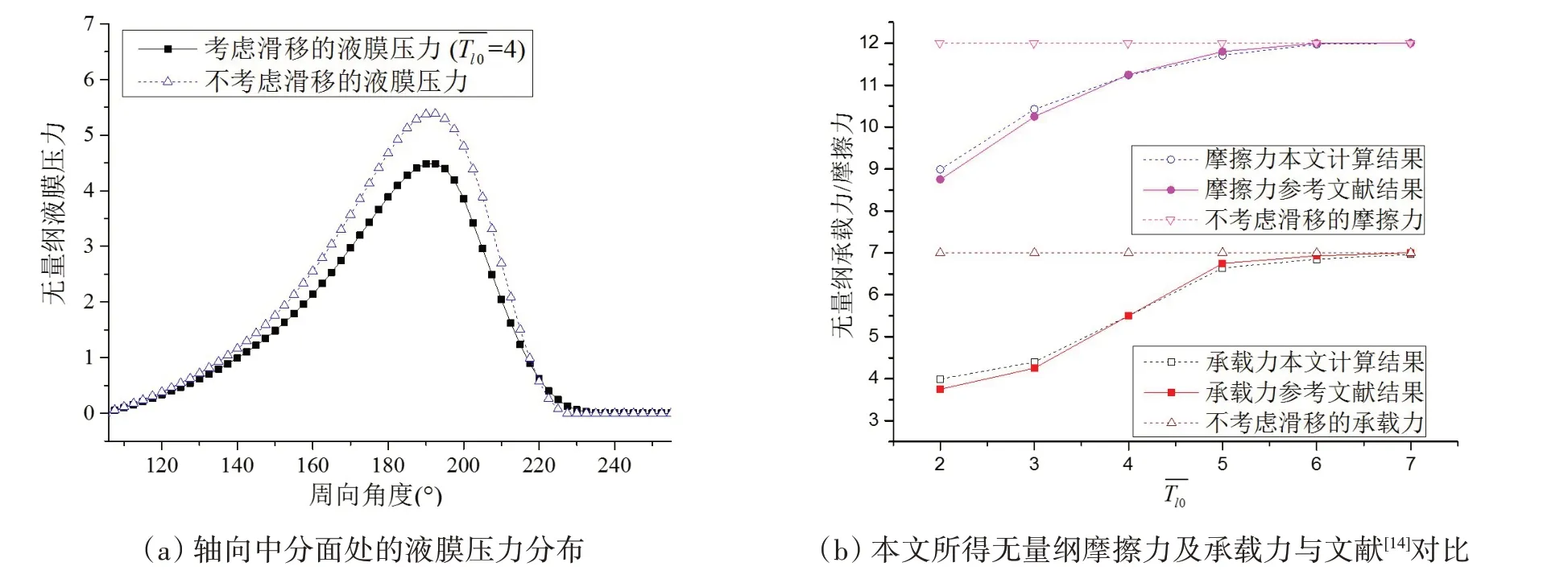
图4 不同模型下的轴承性能Fig.4 Bearing performance with different models
3 结果与讨论
采用本文提出的模型对参数如表2 所示的轴承进行仿真,本算例中轴瓦工作表面为聚四氟乙烯(PTFE)薄膜,基体为铝合金,轴瓦会产生少量变形,但由于PTFE 膜较薄,引起的变形较小(有限元分析结果表明,在转速50 r/min 下,考虑轴瓦变形时液膜厚度变化量为0.55 μm),且几乎不影响规律分析,因而本部分忽略轴瓦变形的影响。通过有限元分析得到转子的挠曲变形曲线,对轴颈各节点的挠曲变形量进行线性拟合,得到轴颈在竖直面内的倾角约为0.015 mrad。轴由金属材料制成,其表面能远大于PTFE,因此液膜在轴表面的极限剪应力远大于轴瓦表面,故而界面滑移通常只产生于轴瓦界面。本算例采用文献[7]测得的油-PTFE界面的极限剪应力(τl=1126.94 Pa)。
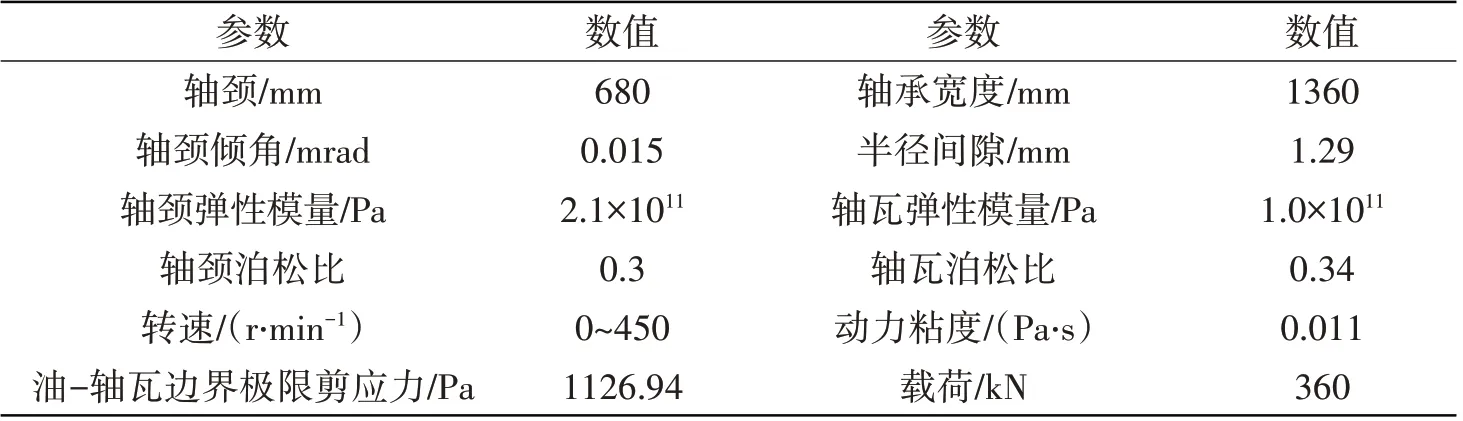
表2 轴承参数Tab.2 Bearing parameters
利用表2 中的轴承参数进行了网格无关性分析,不同网格下轴承性能计算结果对比如表3 所示。为兼顾计算精度与效率,本文计算采用240×160的矩形网格。

表3 不同网格下的轴承性能计算结果Tab.3 Results of bearing performance versus grid numbers
3.1 界面滑移对轴颈倾斜轴承性能的影响
分别考虑界面滑移/不考虑界面滑移对轴颈倾斜下的轴承性能进行了分析,图5为50 r/min时轴承的压力分布。可见,轴颈倾斜时,最高液膜压力靠近轴颈下沉端;对比图5(a)与图5(b)可以发现,在相同载荷条件下,考虑界面滑移增大了轴承最大液膜压力。这是因为考虑界面滑移时轴承承载能力下降,因此相同载荷条件下,考虑界面滑移时偏心率增大,导致压力梯度增大,压力峰较为陡峭。
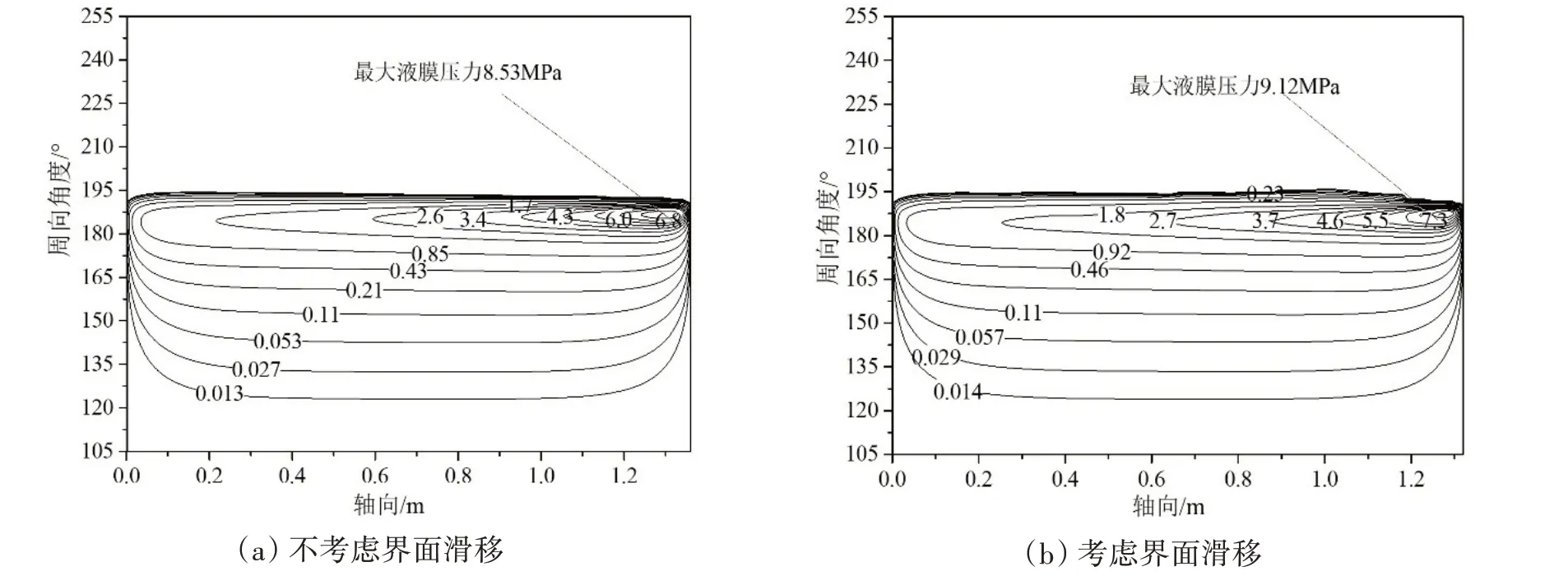
图5 50 r/min下轴承压力分布Fig.5 Pressure distribution of the bearing with a rotational speed of 50 r/min
液膜厚度是评价轴承运行是否安全的重要指标,也是判断轴承润滑状态的主要依据之一。图6(a)为不同截面处的液膜厚度分布,可见轴颈下沉端轴承的最小液膜厚度远小于中分面处的最小液膜厚度,说明轴颈倾斜显著恶化了轴承润滑特性;考虑界面滑移时最小液膜厚度有所减小,说明界面滑移削弱了轴承承载能力,轴承需要更大的偏心率才能平衡外部载荷。图6(b)为摩擦系数随转速变化关系图,可见考虑界面滑移时摩擦系数显著下降,因此可利用该原理对轴承进行优化设计。
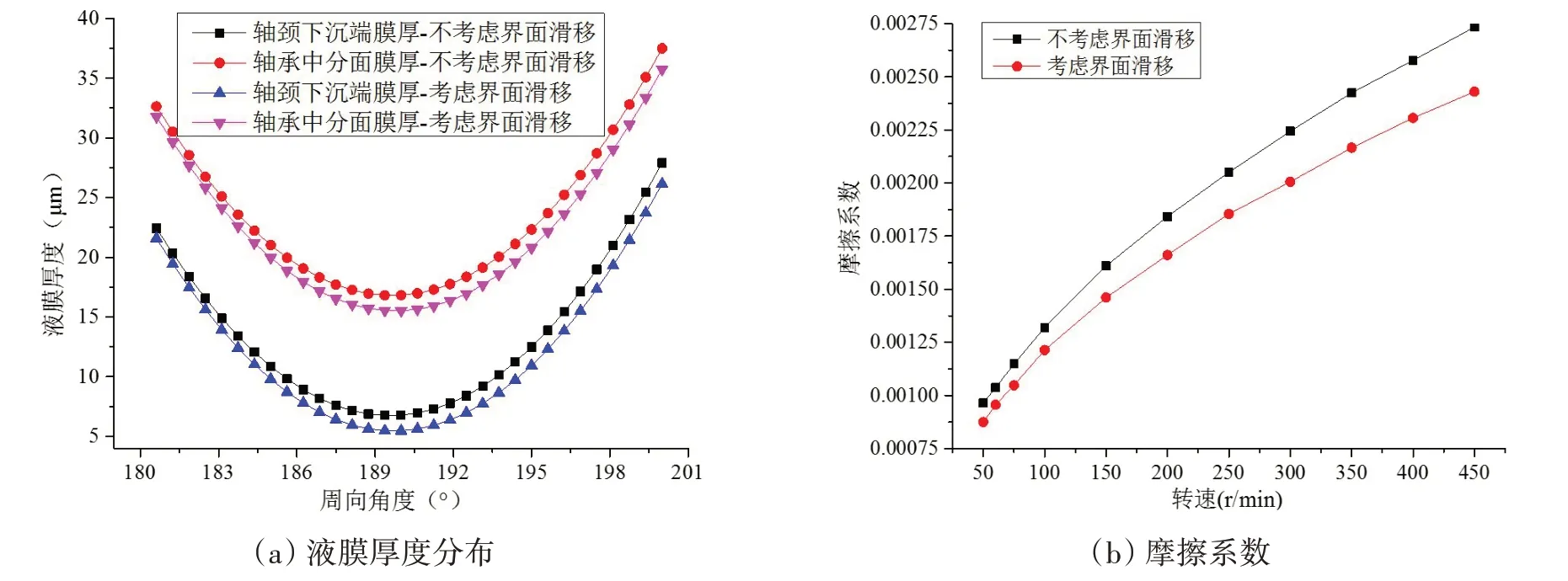
图6 界面滑移对关键特性参数的影响Fig.6 Influence of wall slip on the key characteristic parameters
3.2 局部紊流对轴颈倾斜轴承性能的影响
分别考虑局部紊流/不考虑局部紊流对轴承性能进行了分析。图7所示为转速400 r/min下轴承液膜压力分布。可见相同载荷下,考虑局部紊流时最大液膜压力减小,这是因为考虑局部紊流时轴承的承载能力增大,因而偏心率减小,压力峰相对平缓。
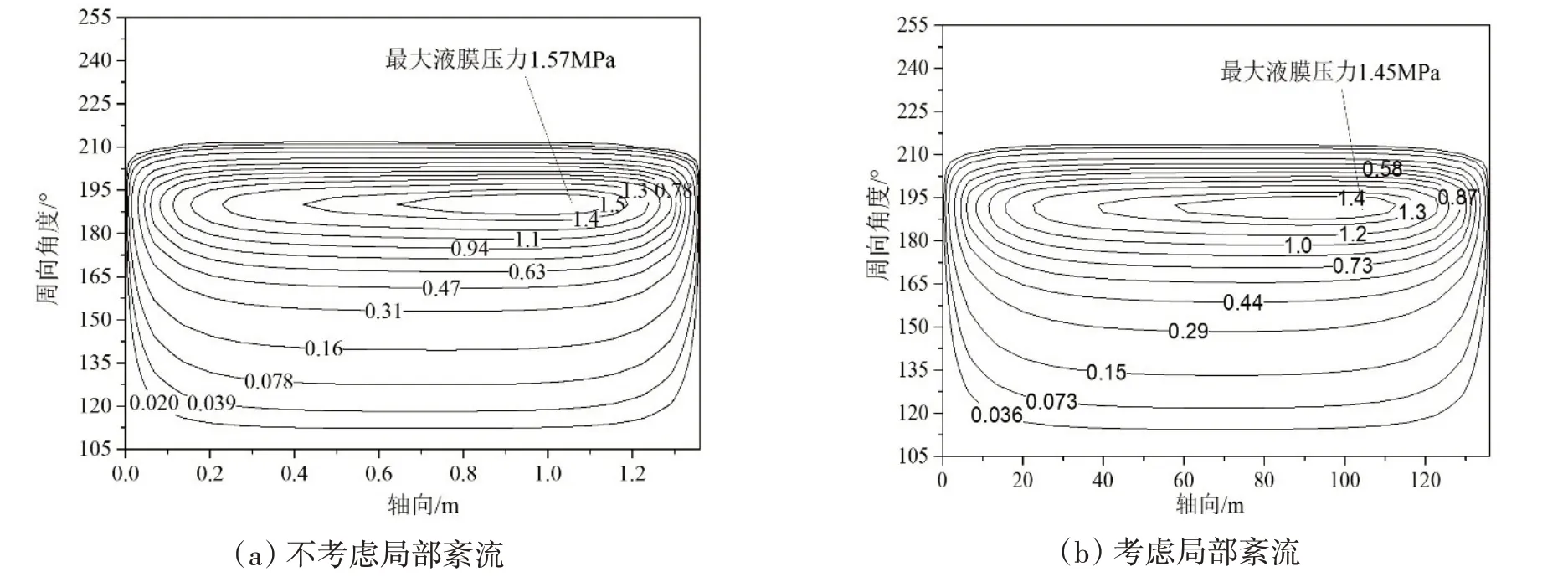
图7 400 r/min下轴承压力分布Fig.7 Pressure distribution of the bearing with a rotational speed of 400 r/min
图8为两种模型下轴承关键特性图。由图8(a)可见考虑局部紊流时,最小液膜厚度有所增大,这是由于局部紊流提高了轴承承载能力,因而偏心率适当减小即可与外部载荷相平衡。图8(b)所示的摩擦系数随转速变化关系图表明,局部紊流增大了轴承的摩擦系数,且随着转速的升高紊流区域增大,摩擦系数的变化量增大。
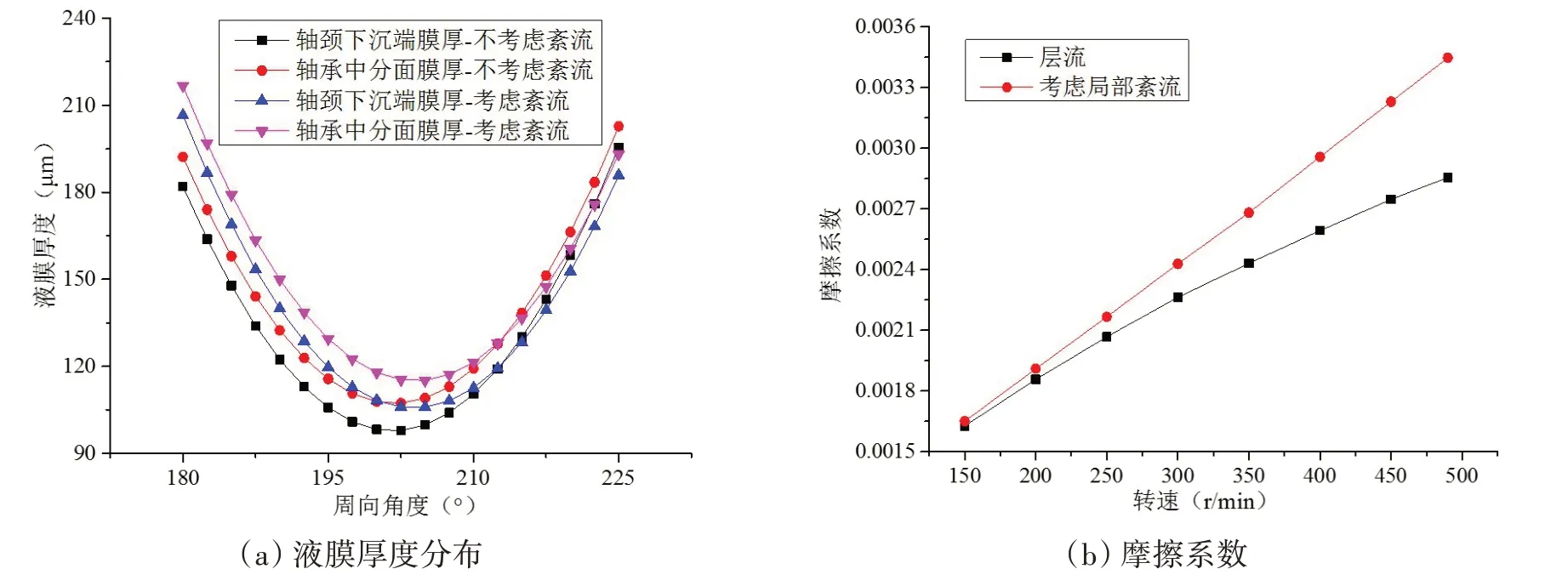
图8 局部紊流对关键特性的影响Fig.8 Influences of local turbulence on the key characteristics
3.3 界面滑移与局部紊流的综合影响
综合考虑界面滑移与局部紊流的影响对轴承性能进行了分析。图9为不同模型下轴承最小膜厚随转速变化关系图。由图可见,转速低于250 r/min 时,紊流对最小膜厚影响较小,界面滑移对膜厚的减小作用占主导,综合考虑界面滑移和局部紊流所得结果与仅考虑界面滑移的结果较为接近。随着转速逐渐升高,紊流区域增大,最小膜厚的变化量也随之增大,逐步与界面滑移引起的液膜厚度减小相抵消,当转速达到450 r/min时,综合考虑界面滑移与局部紊流所得结果与不考虑两因素所得结果较为接近。
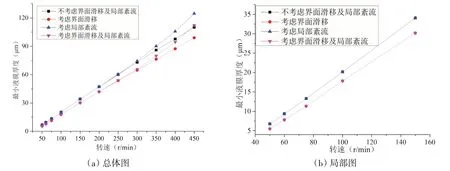
图9 多种模型下最小液膜厚度随转速变化关系图Fig.9 Minimum film thickness versus rotational speed for different models
图10 为不同模型下轴承摩擦系数随转速变化关系图。由图可见,相比最小膜厚,局部紊流对摩擦系数的影响更为明显。转速增大至150 r/min后,紊流对摩擦系数的影响逐渐增大,逐步抵消界面滑移引起的摩擦系数减小;当转速达到350 r/min时,综合考虑界面滑移与局部紊流所得结果与不考虑两因素所得结果较为接近。
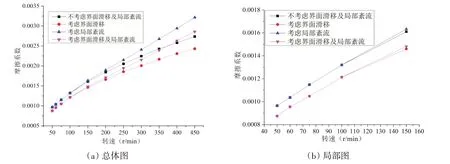
图10 多种模型下摩擦系数随转速变化关系图Fig.10 Friction coefficients versus journal speeds for the different models
4 结 论
本文推导得到了考虑界面滑移及局部紊流的广义雷诺方程,从而建立了一种考虑界面滑移和紊流的轴承分析模型,在此基础上分析了界面滑移、局部紊流及两因素的耦合对轴承性能的影响。主要结论如下:
(1)轴颈倾斜下,最大液膜压力向轴颈下沉端移动,轴颈下沉端液膜厚度显著小于轴承中分面,说明轴颈倾斜严重恶化了轴承的润滑性能。
(2)考虑界面滑移时轴承的承载能力降低,压力峰值升高,最小膜厚减小,但同时摩擦系数降低,可利用该特性进行轴承优化。在载荷不变的条件下,考虑局部紊流时压力变化较为平缓,最小膜厚增大,同时摩擦力增大,且随着转速升高,局部紊流区域增加,紊流的影响更加显著。
(3)综合考虑界面滑移与局部紊流时,低速下,界面滑移对液膜厚度与摩擦系数的减小作用占主导;随着转速的升高,局部紊流对液膜厚度与摩擦系数的增大作用逐渐增强,转速升高至350 r/min 时与界面滑移引起的液膜厚度与摩擦系数减小相抵消。
