FeCr多晶合金拉伸行为的分子动力学模拟
2023-09-20梁珍瑛杜风娇刘建刚
梁珍瑛,杜风娇,刘建刚,林 权
(武夷学院机电工程学院 福建 武夷山 354300)
0 引言
以Fe为基底的富Cr合金广泛应用于基建、汽车和航天领域,在不锈钢材料中发挥着重要的作用,尤其是在高温应用领域。由于FeCr合金优异的几何稳定性,抗腐蚀和抗氧化性能,其可以作为核聚变反应堆的主要结构材料[1-4]。核反应堆的内部材料一般处于中子和质子连续的辐照环境下,这些高能粒子对晶格的冲击会引起级联反应,造成材料结构内部产生大量微观缺陷,例如点缺陷、空位、位错环等。这些微观缺陷进而阻止位错的运动,造成材料的硬化,从而减少材料的服役时间。
不同温度下的缺陷积累的实验表明,FeCr合金中位错环在辐照下成核并缓慢生长,尤其是在较低温度下;升高温度会使位错环的面积更大、密度更低。添加Cr可以使位错环的成核和生长得更快,并且位错环的密度随着温度的升高而降低,同时位错环的尺寸增加。这意味着Cr对缺陷稳定性有很大影响。Fe中的缺陷在温度大于750 K时开始收缩或消失;然而当添加Cr时,实验观察到位错环的收缩和运动被显著抑制[5-6]。
由于原子尺度下实验的限制,研究人员开展了针对FeCr合金中的点缺陷和位错环的模拟工作[3-4][7-10]。例如,吴喜军等[10]对FeCr合金中Cr原子与空位以及间隙原子的结合能研究表明Cr原子与合金中第一近邻空位的结合能最低(61 meV)。贾丽霞等[8]利用分子动力学和迈氏蒙特卡洛方法对不同温度不同Cr浓度下的FeCr合金Cr在位错环上的偏析行为进行了研究,结果表明位错环引起的应力场可以促进Cr在位错环外围进行偏析,而且位错环的类型和尺寸对Cr的偏析浓度没有显著影响;Cr浓度的增加可以提升Cr的偏析量,而温度的升高则会使这一趋势降低[2]。绳淦文等[2]采用ReaxFF反应分子动力学对原子尺度下FeCr合金的氧化过程进行了模拟研究,揭示了与实验观察结果一致的内层FeCr氧化膜形成机制。
以上研究主要集中在点缺陷和位错对FeCr合金的力学行为影响,实际应用中主要为多晶合金,其中晶界起着重要作用[11-12]:晶界可以吸收或者发射点各类晶体缺陷,例如点缺陷和位错[13]。晶界与其他缺陷之间的作用对材料的力学行为有着本质的影响,因此,研究FeCr合金的多晶合金可以帮助理解晶界对其力学行为的作用。
本文基于分子动力学,对FeCr合金二维多晶体进行了建模,研究了不同Cr含量的FeCr合金(0~20 at%)的弹性性质以及拉伸变形行为,分析了Cr含量对合金极限拉伸强度的影响;通过对变形过程中原子结构的分析,研究了其破坏机制。
1 研究方法
1. 1 模型建立
为了研究FeCr合金的拉伸力学性能,本文采用了Voronoi方法建立了FeCr二维多晶模型。首先建立晶向为X[0-11],Y[100],Z[011]的纯铁体心立方结构(body-centered cubic,BCC)原胞,控制晶粒的数量以原胞作为种子点生成不同的晶粒。最后通过随机替换不同比例的Fe原子生成FeCr合金。
图1为生成的多晶模型,采用了OVITO软件进行可视化[14]。如图1所示,晶粒在X-Y平面内的晶向和位置随机,Z方向为[011]方向。本文基于共近邻原子分析(common neighbor analysis,CNA)方法分析了多晶结构,白色原子表示该原子为非晶体无序结构,在图中即为晶界位置,蓝色原子表示BCC结构。本研究随机生成了12个晶粒,晶粒的位置和取向随机,模型共包含约20万原子。为研究不同Cr组分对FeCr多晶拉伸力学行为的影响,生成了5种不同组分的FeCr合金。(Cr=0%,2%,,5%,10% 和20%)。

图1 FeCr多晶原子模型
1.2 模拟方法
原子尺度的模拟手段主要为第一性原理计算,分子动力学(molecular dynamics,MD)与蒙特卡洛方法。为了掌握原子尺度下材料的变形机制,本研究采用了经典MD模拟方法,使用了开源代码LAMMPS[15]。分子动力学的准确度依赖于其所使用的力场(又称势函数),嵌入原子势(embedded atom method,EAM)被广泛应用于金属的力学性能模拟。本文采用了 BONNY G等[16]开发的EAM势,该势函数可以很好地预测FeCr合金的点缺陷能量,位错结构以及热力学行为。EAM势作用下,单原子i的能量如式(1)所示:
(1)
其中rij为原子i和j之间的距离,φαβ为对势函数(其中α和β表示原子种类),ρβ为β原子种类的电子密度分布,Fα为嵌入势函数[17]。
为了研究FeCr合金在室温(300 K)下的拉伸力学响应,先将模型升温至300 K并至于等温等压(NPT)系综下弛豫20 ps,该步骤的目的是为了消除引入晶界时模型产生的内应力并获得热力学平衡态的晶界构型。接下来对模型进行拉伸加载,采用了应变加载方法并设置应变率为109s-1。对模型的三个方向施加了周期边界条件使其更接近整块体材料在真实情况下的力学性质,拉伸过程中使用NPT系综,利用Nose-Hoover热浴控制系统温度,施加X方向的应变并保持Y和Z方向的压力为0 Pa。动力学采取了velocity-Verlet积分方法,时间步长设置为0.001 ps。
2 模拟结果及分析
2.1 弹性模量
据已有实验观测,FeCr合金的性能极大程度上取决于Cr的含量[5]。因此,Cr浓度的变化对FeCr合金的微观结构及其力学行为有着显著的影响。为了研究FeCr在极端辐照环境下的力学性能,基于300 K下不同Cr组分的平衡后的构型,计算了FeCr合金在室温下的弹性模量,并与实验和理论计算结果进行了对比。在经过20 ps弛豫时间后,FeCr多晶中的3个小角度晶界转化为均匀排列的位错墙,与现有理论结果相符合。进一步通过施加小弹性变形,并计算出模型的应力应变关系,从而获得了体模量(B,bulk modulus)和剪切模量(G,shear modulus)。由于多晶材料内部晶粒的随机性,其常被考虑为各向同性材料,故只需两个相互独立的材料常数。本文采用了体模量和剪切模量,此外常用的杨氏模量(E)和泊松比(υ)可以通过式(2)进行转换。
(2)
如图2所示合金体模量和泊松比随着Cr含量增加的变化趋势。对于体积模量在Cr组分为0~2 at%时,本文的计算结果和实验结果误差小于3%。组分为2~10 at%时,其变化趋势相反,但误差仍小于10%[18]。密度泛函理论(density functional theory)计算结果趋势与本文的计算结果趋势相同,误差稳定在约为7%。EMTO理论计算结果呈现出先下降后上升的趋势,与本文预测趋势差距较大。剪切模量随着Cr含量的增加而降低,呈现出近似线性关系,Cr含量为20 at%时剪切模量降低了6 GPa(7%)[1,19]。DFT和实验的预测结果均为剪切模量随着Cr含量的增加而增大。本文的预测结果与实验结果整体误差均小于6%[18]。本文对体模量和剪切模量的预测整体误差较小,证明了势函数的可靠性。

注:MD表示本文的分子动力学计算结果;Exp.为文献[18]中的实验结果;EMTO表示exact muffin-tin orbita理论计算结果;DFT为密度泛函理论计算结果[1]。图2 体积模量和剪切模量随着Cr含量增加的变化趋势
2.2 拉伸加载下的应力应变响应
基于300 K下平衡后的构型,对不同Cr组分的FeCr合金进行了拉伸加载,获得了应力应变响应。图3给出了不同Cr组分FeCr合金的应力应变曲线。

图3 不同Cr组分下FeNi合金的工程应力应变曲线
首先,可以看出拉伸变形过程中的共同点:不同组分的FeCr合金首先进入弹性变形阶段,在应变为0.05左右时弹性能突然释放,开始发生塑性变形。其次,不同的浓度的Cr对于FeCr合金的拉伸力学响应有着明显的影响。从纯Fe到5 at%组分的合金随着Cr含量的增加其弹性应变逐渐增加,对于10 at%和20 at%组分的合金其弹性应变反而降低。在塑性流动阶段,其流动应力水平变化并无明显规律。
对应力应变的最高点进行提取,得到了不同Cr组分下的FeCr合金的极限拉伸强度(ultra-tensile stress,UTS)和最大拉伸应变(maximum tensile strain,MTS)。图4给出了FeCr合金的UTS和MTS随着Cr组分增加的变化趋势。

图4 FeCr合金的极限拉伸强度和最大拉伸应变随Cr组分增加的变化趋势
随着Cr组分的增加,UTS和MTS呈现出先增加后减少的趋势。在Cr组分为5 at%时UTS和MTS最大,UTS为5.18 GPa,相对于纯铁的4.82 GPa增加了7.5%。继续增加Cr的组分则会使得UTS减小。例如在Cr含量为10%和20%时,UTS约为4.52 GPa,相对于纯铁的UTS减少了6.2%。由此可见,适当的增加Cr的含量可以增强FeCr合金的极限拉伸强度,然当含量等于或超过10 at%时,FeCr合金强度会迅速降低。
2.3 拉伸变形微结构演化
对拉伸过程中的变形进行进一步分析,基于变形过程中没有发生相变,因此可以使用非体心立方结构的无序原子比例来表示晶界原子比例。基于OVITO软件,分析了不同Cr组分FeCr合金在拉伸过程中无序原子的比例,见图5所示。

图5 不同Cr组分下缺陷原子比例随应变的演化趋势
在应变为零的状态下,10 at%和20 at%的多晶合金中无序原子比例高于其他组分的合金。这是因为大量的引入Cr原子在平衡过程中与晶界作用,使得晶界结果更加无序。持续的增加应变至0.05左右引起无序原子的跳跃式增长,这里开始了大量的位错发射和晶界移动等塑性变形行为。
图6为变形过程中FeCr多晶的原子示意图。
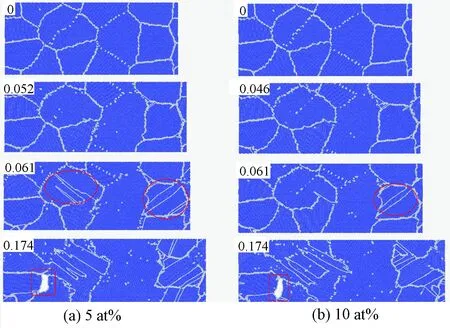
注:基于OVITO的共近邻原子分析方法绘制,其中蓝色为BCC结构原子,白色为无序结构原子。每个组分包含四个应变下的原子示意图,对应的应变在每幅图的左上角标出。椭圆形标出了晶粒扩张形成的新晶界,方形为形成孔洞的位置。图6 5at%和10at%Cr组分下FeCr二维多晶的原子变形示意图
可以看出在应变为零时,一部分小角度晶界转化为位错墙,随着应变的增加,位错随之移动。位错的移动代表着塑性变形的发生,但由于其数量极少,并未对应力应变曲线产生明显的影响。继续增加应变,塑性变形的主导机制开始作用,即晶粒转动。在图6(a)和图6(b)中应变为0.061时,观察到新的晶界(图中由椭圆形标出)。这是由于应力的增长导致了一些小晶粒的长大,引入了新的晶界。新的晶界继续与晶体中已存在的位错发生反应,引起多晶整个晶界结构网络的持续变化(图6,应变=0.174)。最终空洞在三叉晶界中形核并长大,引起材料的失效。
3 结语
本文基于分子动力学计算了不同Cr组分下(0~20 at%)FeCr二维多晶合金的弹性常数并与实验进行了对比,研究了其原子尺度下的拉伸变形行为,分析了其破坏机制。研究结果表明:(1)分子动力学计算的二维多晶的体模量和剪切模量与实验式偏差小于7%,验证了本文使用的势函数的可靠性;(2)Cr组分为5 at%时FeCr合金的极限拉伸强度达到最大,随着Cr组分继续增加极限拉伸强度减小;(3)不同组分下FeCr合金的失效机制类似:空洞从最薄弱的三叉晶界处形核。
