复杂微小通道内超临界CO2-水换热特性试验研究

金 峰,陈德奇,*,胡 练,黄彦平

(1.重庆大学 能源与动力工程学院,重庆 400044;2.重庆科技学院 机械与动力工程学院,重庆 400044;3.中国核动力研究设计院 中核核反应堆热工水力技术重点实验室,四川 成都 610041)

随着能源的不断消耗及伴随的环境问题,越来越多的人开始关注对能源利用效率的提升及“碳中和”目标。近年来,超临界CO2布雷顿循环的发展受到了国内外学者的广泛关注,其具有高紧凑性、高效率及减排等优势,在核能、太阳能、地热能等领域具有较好的应用前景[1-2]。超临界CO2在临界区附近(7.38 MPa,31.3 ℃)呈现高密度、低黏性及高可压缩性等特性,可降低泵输出功率,结合较高的透平入口温度(550 ℃以上),使得超临界CO2布雷顿循环拥有更高的热循环效率,成为高温气冷堆研究中的重要对象之一。由于超临界CO2布雷顿循环透平出口温度高,为充分利用循环过程中的有效热,回热器及预冷器成为回热过程的关键设备。印刷电路板式换热器(PCHE)作为一种新型换热器,具有紧凑性高、效率高及耐高温高压等优势,相比传统的管壳式换热器,其体积可减少85%左右,是超临界CO2能源系统的首要选择[3]。此外,在预冷工况下,超临界CO2快速冷却至临界区域附近,由于换热过程中流体发生强烈的物性变化,从而可能存在传热强化或弱化现象,进一步影响换热器的整体性能,因此,研究超临界CO2在临界附近的冷却传热十分必要。

实验数据是超临界CO2传热特性研究的重要依据。针对临界区附近超临界CO2在PCHE内的实验研究,Kruizenga等[4-5]研究了半圆形通道内超临界CO2的冷却传热,并将实验结果与现有关联式进行了对比,其预测误差在20%以内,而在临界温度及压力附近,关联式过高评估了换热能力。Li等[6-7]基于Kruizenga等[4-5]的实验数据,通过概率密度时间平均法,提出了新的超临界CO2传热关联式,其预测结果显示有90%的实验数据落在±25%以内。Chu等[8]通过直通道PCHE内超临界CO2实验发现,相同质量流速下,超临界CO2传热性能优于水,并在高压条件下,超临界CO2呈现出更好的综合性能。基于获得的实验数据,他们提出了直通道PCHE在超临界及跨临界下的传热关联式。Park等[9]开展了直通道PCHE内跨临界、远离临界及临界区域工况下的实验研究,并对比了平均焓方法与离散方法对实验数据处理结果的影响,结果表明离散法在设计预冷器时是有效的。Baik等[3]对预冷器条件下的Z字形PCHE开展了实验研究,其入口温度及压力范围分别为26～43 ℃及7.3～8.6 MPa,基于实验数据提出了新的传热及压降关联式并开发了计算程序。Cheng等[10]将100 kW PCHE作为预冷器进行了实验测试,并对比了不同入口温度、流量及压力对整体换热系数及换热量的影响。Li等[11]研究了CO2入口温度及压力对Z字形PCHE整体传热能力的影响,并采用工作点(考虑工作温度及压降)评估整体换热系数,结果表明当工作点接近1时,PCHE呈现出更好的性能。Pidaparti等[12]则针对矩形及翼型通道PCHE内超临界CO2热工水力性能进行了评估,并提出了努塞尔数半经验关联式,其平均相对偏差分别为±15.4%与±8%。Liu等[13-14]研究了超临界CO2在直通道及Z字形通道PCHE内的流动传热性能。结果表明,当超临界CO2从类气态区域冷却至拟临界区域时,对流传热得到强化,并分别针对直通道及Z字形通道提出了传热及摩擦关联式,结合综合性能因子(Nu/Nu0)/(f/f0)1/3,发现当Re和Pr较大时,Z字形通道的整体性能明显高于直通道。

目前关于预冷器条件下PCHE内的研究仍有限,同时Z字形通道PCHE内的局部实验数据较少。因此,本文基于超临界CO2-水试验回路,设计并开展Z字形通道PCHE内超临界CO2-水换热实验,获得冷热流体温度沿程分布特征,并研究压力、温度及流速对超临界CO2局部整体换热系数及对数平均温差的影响,进一步使用整体法与分段法对这些参数进行对比,评估两种方法带来的差异。

1 实验装置

1.1 实验系统介绍

实验系统的整体布置如图1所示,超临界CO2-水系统循环示意图如图2所示。该系统由CO2回路、水回路、充放气旁路及冷却旁路组成。CO2回路及水回路用于提供实验本体的进口及出口条件,充放气旁路用于辅助CO2回路的压力调节,冷却旁路则作为CO2回路及水回路的热阱。在实验开始前,首先使用充放气旁路的真空泵进行真空处理,然后再通过汇流排将气瓶内99.99%的CO2冲入CO2回路内。当CO2回路压力初步稳定时,开启气体增压泵对CO2进行增压直至系统压力达到临界压力。在该过程中,冷水机组1始终处于运行状态,从而对系统内CO2进行降温以确保CO2处于液态或类液态。随后,通过电动阀隔离辅助增压设备,并开启CO2回路的循环泵及水侧的循环泵。进一步地,打开直流加热电源控制预热段的加热功率,使系统内的CO2与水达到指定温度,并结合减压阀将CO2回路系统压力控制在10 MPa以下。之后,超临界CO2流入PCHE实验本体中并与水进行换热,在本体内的冷却过程完成后,进一步通过套管换热器与冷水机组换热,使超临界CO2冷却至拟临界温度以下,最终返回磁力泵。水侧运行流程与CO2侧类似,在实验本体内换热升温后通过套管换热器进一步降温,从而控制水侧的系统温度。

图1 实验系统整体布置

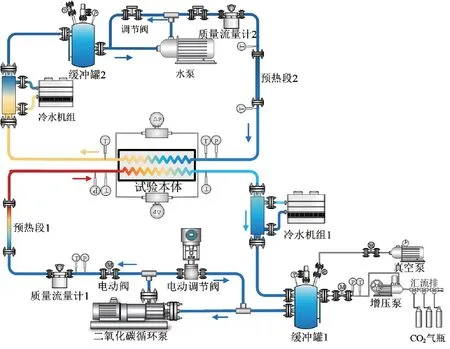
图2 超临界CO2-水试验回路示意图

CO2侧及水侧的流量均通过变频器及旁路控制阀门进行控制与调节。其流量均采用科氏力质量流量计(误差为±0.15%,量程为0～960 kg/h)进行测量。压力传感器最大量程为16 MPa,差压变送器最大量程为100 kPa,两者测量误差分别为±0.05%及±0.075%。实验段所有温度点均采用T型热电偶(Ⅰ级精度)进行测量,其最大测量温度为200 ℃。另外,当实验参数达到预定设计工况且系统稳定运行时,所有流量、压力及温度数据均通过数据采集模块进行收集并最终储存在终端计算机。

1.2 测试本体

为研究超临界CO2的传热性能,本研究采用SS316L作为固体材料,设计并制造了半圆Z字形通道PCHE试验本体。图3为试验本体装配图,由4对法兰、换热元件及相应的连接件组成。其中靠近法兰位置处均安装有热电偶及压力压差传感器,分别用于测量换热器的进出口温度、进口压力及两端压差。测试本体组成及温度测点位置如图4所示,由7层板组成,包括2层盖板、2层水通道板、2层测量板及1层CO2通道板。冷热通道的结构参数保持一致,如表1所列。PCHE试验本体测点的轴向分布位置及实物图如图5a、b所示,通道核心长度为485 mm,上下水侧通道内各布置10个热电偶,相邻测点的间距为43.44 mm,用于测量流体温度,同时,上下测量板各布置11个热电偶,用于测量冷热通道之间的壁温,壁面测点与流体温度测点沿轴向交错排布,共42个测点。图5c为局部测点示意图,主流温度及壁面温度测点分别位于每层板的中间位置。

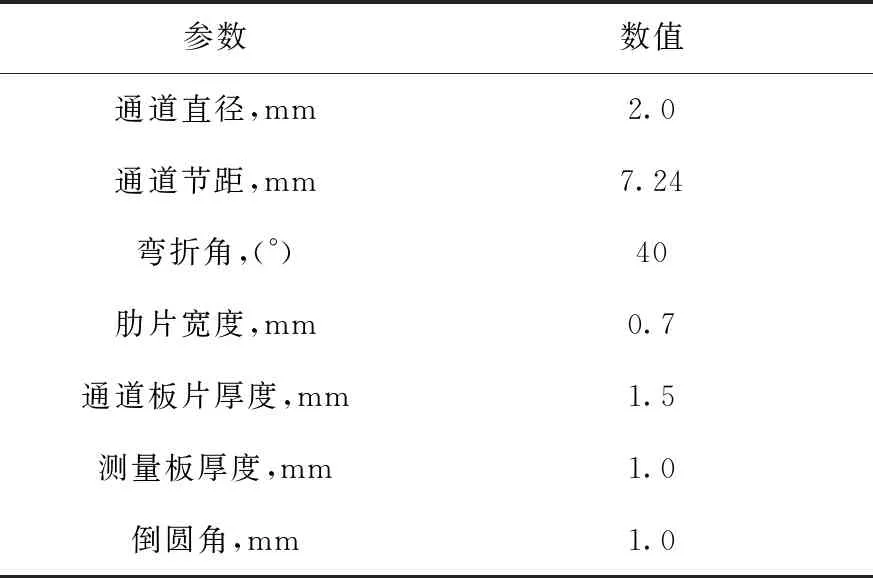
表1 Z字形通道PCHE参数

图3 试验本体装配图

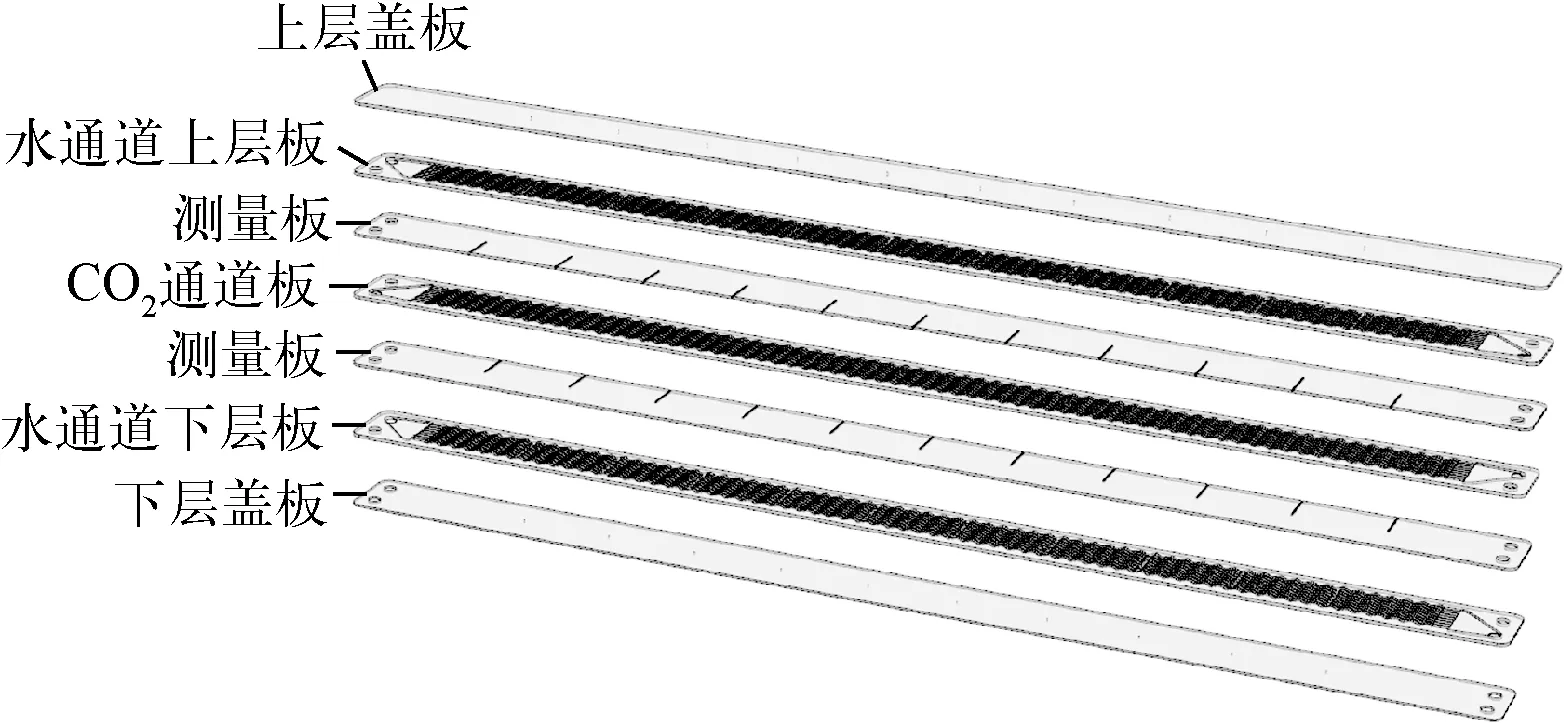
图4 换热元件组成

a——轴向温度测点;b——实物图;c——局部测点示意图

1.3 数据处理及不确定性分析

在Z字形PCHE内,换热器整体换热系数Ui及局部对数平均温差ΔTLMTD,i按下式计算:

(1)

(2)

ΔTLMTD,i=

(3)

其中:qh,i为局部热流密度;Qh,i为CO2的局部换热速率;ACO2,i为局部热通道的换热面积;TCO2,i和TH2O,i分别为CO2侧和水侧的局部主流温度。

在计算换热速率Qh,i前,首先基于冷热侧进出口温差分别计算CO2与水侧的换热速率Qh与Qc,评估实验过程中的热平衡率η(式(4)),所有数据结果的η值均在94.5%以上,因此认为实验数据有效。然后对上下水侧主流温度进行平均,得到水侧的换热速率Qc,i(式(5)),进一步得到热侧的换热速率Qh,i。

(4)

(5)

其中,Tbu和Tbl分别为上层和下层局部通道温度。

CO2通道内的主流温度Tb,i通过查询NIST数据库[15]的hi与系统压力p获得,焓值基于式(6)的热平衡公式计算:

hi+1=hi+QCO2,i/mCO2

(6)

本文采用整体法及分段法对计算结果进行了对比。整体法中,Uz与ΔTLMTD,z计算公式如式(7)、(8)所示,即通过常规进出口温度进行计算。

ΔTLMTD,z=

(7)

(8)

分段法中,对上述的局部计算结果进行平均获得Uf和ΔTLMTD,f,如式(9)、(10)所示。

(9)

(10)

实验过程中的测量不确定性基于Moffat[16]的方法进行计算。假设y是变量x1,x2,…,xn的函数,则y的绝对误差及相对误差计算公式如式(11)、(12)所示。从而得到对数平均温差及整体换热系数的相对误差分别为11.3%、18.9%。

(11)

(12)

2 结果分析

为排除进出口端头对换热分析的影响,本文仅取换热核心区域的结果进行对比,探讨不同工况条件对超临界CO2-水在核心区域换热性能的影响。试验工况范围列于表2。

表2 试验工况范围

2.1 CO2入口温度对整体换热性能的影响

热侧不同入口温度下的工况列于表3,工况A-1、A-2、A-3的入口温度分别为50.7、71.0、87.1 ℃。3种工况参数下的沿程参数变化示于图6。可以看出,随着入口温度的升高,整体对数平均温差水平提高,尤其在CO2入口位置提升明显。在超临界CO2与水进行换热的过程中,其热侧温度逐渐靠近拟临界区,在该区域内比热容显著升高,沿程温降减小,随着温度的继续降低并远离拟临界区,沿程温降将重新增大,冷热通道间出现温度夹点。因此,对数平均温差呈现中间低两边高的沿程分布趋势。同时,在拟临界区附近,由于超临界CO2强物性变化,整体换热系数U明显升高,最大值可达3 338 W/(m2·℃)。然而,随着入口温度的增大,拟临界区域及传热强化区域逐渐向末端移动,但几乎不影响强化传热峰值水平,同时,由于对数平均温差提升,工况A-3的换热速率相比工况A-1提升了22.4%。

表3 入口温度工况

图6 入口温度对沿程参数的影响

2.2 CO2入口质量流速对整体换热性能的影响

在热侧压力8.02 MPa、入口温度50 ℃下,不同入口质量流速(311.72、495.37 kg/(m2·s))下的工况列于表4。入口质量流速对沿程参数的影响示于图7。可以看出,随着入口质量流速的提升,超临界CO2沿程温度梯度降低,由于通道内CO2的湍流强度增大,换热能力提高,整体换热系数平均上升11.69%,且在拟临界区域传热强化效果更明显,其最大值从3 305 W/(m2·℃)升至4 193 W/(m2·℃),提高了26.87%。从图7b也可以看出整体换热系数沿程变化梯度更加明显。然而,在当前的工况下,对数平均温差水平及沿程分布趋势却没有明显改变,这是由于随着整体换热系数的增加,水侧温度的沿程变化速率增大,从而缩小了CO2流速变化带来的温度差异。为了更加直观地观察变物性特征下不同流速对CO2-水换热特性的影响,本文对不同温度下的整体换热系数进行了平均,结果如图8所示。可以看出,当CO2主流温度靠近拟临界区时,整体换热系数明显提升,且最大值对应的温度高于拟临界温度,这是由于拟临界温度处于缓冲层区域时,在拟临界区域内超临界CO2的比热容及导热系数等物性参数呈现较高水平,增强了边界层至对流主导区域的热输运性能,从而提高了局部换热能力,通道热输运效果更显著[17-18]。

表4 入口质量流速工况

2.3 CO2压力对整体换热性能的影响

不同压力入口工况如表5所列,工况C-1、C-2、C-3的入口压力分别为7.53、8.01、9.08 MPa。3种压力下的整体换热系数沿程分布如图9所示。通过对比可以发现,在7.53 MPa压力(工况C-1)下拟临界区域的整体换热系数相比其他两种工况更高,其值为3 811 W/(m2·℃),而由于工况C-1在出口位置更加接近拟临界温度,水侧温度上升快,且类气态温度下的比热容较小,该工况呈现更低的温度夹点,导致整体换热速率下降。当压力升高至8.01 MPa(工况C-2)时,拟临界温度上升,整体换热系数最大值向换热器中部移动,由于最大比热容相比7.5 MPa下降低,最大整体换热系数降低至3 488 W/(m2·℃),下降了8.48%。同时,由于8.01 MPa下在类气态区域的比热容较高,温度变化相对平缓,对数平均温差升高,从而提高了整体换热水平。当入口温度升高至9.08 MPa(工况C-3)时,拟临界区域靠近CO2入口位置,整体换热系数略有升高后很快下降至较低水平,由于在换热后半程趋向类液态转变过程,比热容快速降低,CO2温度曲线呈现快速下降特征,此时对数平均温差不再呈单调上升的趋势,而是在达到极大值后快速下降。同时,通过观察也可以发现,最小对数平均温差并不一定出现在拟临界温度位置,其主要与冷热流体的沿程热流分布(mcp)有关。通过对不同温度下的整体换热系数进行平均,得到不同压力下整体换热系数随CO2主流温度的变化曲线,如图10所示。7.5、8.0、9.0 MPa所对应的整体换热系数峰值分别为3 828.3、3 466.0、3 281.8 W/(m2·℃)。可以看出,当压力较高时,整体换热系数的峰值明显下降,且随着压力的升高,整体换热系数随温度变化更加平缓。

表5 入口压力工况

图9 入口压力对沿程参数的影响

图10 不同入口压力下整体换热系数对比

2.4 水侧质量流速对整体换热性能的影响

在热侧压力8.02 MPa、入口温度50 ℃下,水侧不同质量流速工况列于表6。两种工况下的沿程参数示于图11。可以看出,相比于整体换热系数,对数平均温差变化更显著。当水侧入口质量流速为249.32 kg/(m2·s)时,CO2侧沿程温度变化速率逐渐递减,而水侧的沿程温度变化速率逐渐增加,换热器温度夹点出现在206.56 mm附近,对数平均温差呈现中间低两边高的分布趋势。随着水侧入口质量流速的提高,由于对数平均温差增大,CO2侧温度快速降低至拟临界温度以下,不同于工况D-1,工况D-2沿程温度下降梯度在CO2出口附近出现明显的升高,与工况C-3结果相似,对数平均温差出现极大值后迅速下降。然而,由于类液态下的CO2流体速度迅速减小,同时伴随着比热容等物性的下降,导致该区域内的整体换热系数处于较低水平。

表6 水侧流速工况

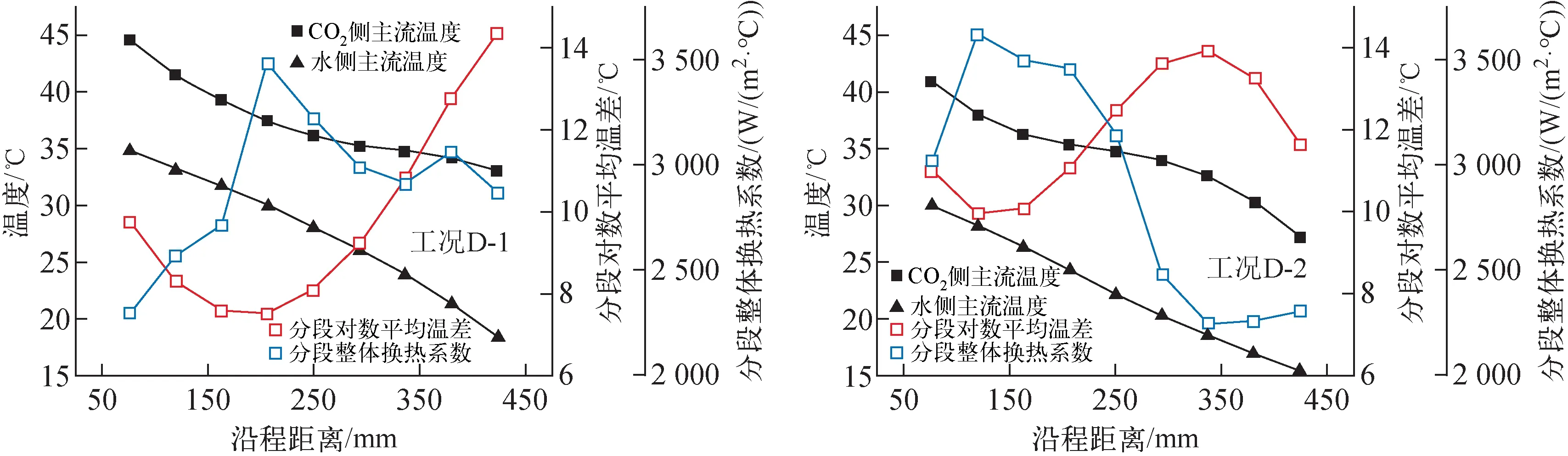
图11 水侧不同质量流速下沿程参数的对比

3 基于整体法与分段法的整体换热系数对比

由于超临界CO2在拟临界区域附近强烈的物性变化,且对数平均温差是基于常物性推导得到的,因此,仅通过进出口温度得到对数平均温差将带来一定偏差,进一步对整体换热系数评估带来影响。为了对比其差异性,本文基于分段法与整体法分别计算了上述工况下PCHE核心区域的平均对数平均温差和平均整体换热系数,结果列于表7。可以看出,在CO2从类气态靠近拟临界区工况中,由于CO2沿程比热容的快速上升,CO2沿程温降逐渐减小,基于整体法得到的对数平均温差明显小于基于分段法得到的结果,且随着入口温度及CO2入口流速的增大,两种方法得到的ΔTLMTD与U差异似乎也越大,U的最大相对误差分别达到59%及25%。而当出现跨拟临界温度工况时,如C-3与D-2,CO2主流温度快速降低并低于拟临界温度以下,沿程对数平均温差出现了极大值与极小值,对数平均温差呈现倒S型的分布趋势,处于高值下的ΔTLMTD与处于低值下的ΔTLMTD近似于“相互补偿”,此时基于分段法平均得到的对数平均温差与常规法得到的对数平均温差更为接近,使得整体换热系数的差异反而减小,从表7可以看到,在C-3与D-2工况下,最大相对误差在5%以内。可以看出,基于整体法得到的对数平均温差的精度取决于局部对数平均温差的分布趋势,并不能够准确表征在强变物性工况下的预冷器整体换热能力,从而可能给评估结果带来影响,因此,建议采用分段方式对靠近CO2临界区域位置运行的PCHE整体换热系数及对数平均温差进行评估,以提高对PCHE设计及评估的准确性。

表7 基于整体法与分段法的参数对比

4 结论

本文基于超临界CO2试验平台,开展了不同工况下复杂微小通道内超临界CO2-水的换热试验研究,探究了压力、温度及流速等参数对超临界CO2-水整体换热特性的影响。得到如下主要结论。

1) 超临界CO2在拟临界区表现出的强变物性特性,使得超临界CO2-水整体换热性能在拟临界区域达到峰值。同时,由于拟临界区在边界层区域的增强作用更为显著,整体换热系数峰值所对应的主流温度略高于拟临界温度。

2) 在当前实验工况下,入口温度的变化对局部整体换热系数的影响较小。同时,较高温度对应的CO2类气态区域的整体换热系数明显小于拟临界区域;当超临界CO2质量流速增加时,通道内的湍流强度增强,整体换热系数显著增加;改变超临界CO2系统的压力时,其物性的变化显著影响整体换热系数水平;超临界CO2的压力增加降低了整体换热系数的峰值,但其随温度的整体分布则更为平缓。

3) 在靠近拟临界工况下,分段法和整体法的计算结果呈现明显差异,而在跨越拟临界工况下,由于对数平均温差的倒S型分布,二者的误差显著减小。鉴于超临界CO2的强物性变化特点,建议基于分段法计算对数平均温差和整体换热系数,以更准确地设计和评估预冷器PCHE的整体换热性能。