装备振动功率谱密度统计归纳误差研究

申加康,徐 俊,张建军,李 贺,万 军

(1.中国航空综合技术研究所,北京 100028;2.西南技术工程研究所,重庆 400039)

GJB150A推荐根据实测数据来确定振动试验条件[1]。美军标MIL-STD-810H中给出了振动、冲击环境的多种统计归纳方法[2]。其中,对于符合正态分布的振动功率谱密度数据,常使用正态单边容差上限方法进行统计归纳[3]。近年来,众多专家对振动功率谱密度数据的归纳方法进行了研究,并将归纳方法应用于飞机、舰船、车辆等装备的试验条件确定[4-19],但尚未有专家对正态单边容差上限的估计误差进行研究。

正态单边容差上限的计算过程涉及到一个关于无限多的样本记录的极限运算,而工程上无法做到极限运算,工程上统计分析的结果只是一个关于上限真值的样本估计,因此对于实际的统计归纳结果一定会有统计误差。根据概率统计知识可知,样本越多,统计误差就越小。然而,通常情况下,获取实测振动数据成本较高,振动功率谱密度样本量不可能获取太多。例如,一个架次飞机试飞,往往就需要耗费大量的人力物力和财力。因此,有必要研究正态单边容差上限估计误差与样本量之间的关系,为预先定量确定实测次数提供参考。

本文推导了正态单边容差上限估计的均方根误差和百分比误差的数学公式,并给出了上限估计误差与样本量之间的定量关系。

1 基于正态单边容差上限方法的统计误差推导

1.1 正态单边容差上限定义

HB20237—2014《军用飞机平台环境测量数据归纳方法》[20]中对正态单边容差上限有着明确的定义。随机变量x的正态单边容差上限估计为在规定的置信度γ下,该值大于其真值xH的概率为100β%,由式(1)和式(2)给出

(1)

(2)

正态单边容差上限的NTL(N,β,γ)为

(3)

置信度取100γ%,分位点取100β%的正态单边容差上限称之为P(100β)/(100γ)上限,其物理意义为这个上限值以100γ%的置信度覆盖了100β%的测量数据点,常用的正态单边容差上限有P95/50上限和P99/90上限。

1.2 正态单边容差上限的均方根误差

由正态单边容差上限的定义可知,当总体期望和总体标准差确定时,100β%覆盖概率的正态单边容差上限xH也随之确定,因此正态单边容差上限xH也是反映总体的一个参数。

(4)

(5)

在进行公式推导之前,先给出概率统计中常用公式

(6)

(7)

(8)

(9)

其中,M的表达式为

(10)

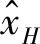
因为:

(11)

所以:

(12)

其中,

(13)

(14)

(15)

(16)

(17)

1.3 正态单边容差上限的百分比误差

正态单边容差上限的百分比误差

(18)

(19)

其中,cv=σx/μx在概率论中被称为变异系数,又称离散系数。根据功率谱密度的物理意义,此处cv为正值。

从式(19)中可以看出,当样本的数量N、置信度γ和覆盖概率100β%一定时,正态单边容差上限的百分比误差受各频点的功率谱密度值概率分布的变异系数cv影响。

需要说明的是,式(19)的百分比误差是一个期望误差,即由N个样本计算得到误差在ε附近波动。

2 正态单边容差上限的百分比误差仿真校验

基于实测振动功率谱密度样本统计归纳的过程,可认为是从某一确定的正态总体中随机选择有限个样本,并基于有限个样本估计总体的上限。由于样本选择的随机性,使得上限估计存在一定的误差。因此,为了验证,可采用如下思路验证式(19)的正确与否:

(1) 给定正态总体的期望和方差,生成一组呈正态分布的数据A,数据个数为1 000 000;

(4) 改变挑选的样本个数N,重复过程(2)～(3),得到不同样本数的上限估计的百分比误差。

根据上述思路,设计多组仿真案例,如表1所示。

表1 仿真案例表Tab.1 Simulation case table

分别计算表1中案例的P95/50上限的百分比误差、P99/90上限的百分比误差以及对应的按式(19)理论计算得到的误差,绘制上限估计误差随样本数量变化曲线,如图1和图2所示。

图1 案例1～案例4的P95/50上限估计误差随样本量的变化曲线Fig.1 The curve of P95/50 upper limit estimation error of case 1 to case 4 as a function of sample size

图2 案例1～案例4的P99/90上限估计误差随样本量的变化曲线Fig.2 The curve of P99/90 upper limit estimation error of case 1 to case 4 as a function of sample size

从图1和图2中可以看出:

(1) 案例1～案例4的仿真结果与理论计算结果基本一致,表明1.3节中推导的正态单边容差上限估计的百分比误差公式是正确的;

(2) 案例3和案例4的仿真结果基本一致,表明正态单边容差上限估计的百分比误差与总体方差和期望的大小无关,而与二者的比值——变异系数相关;

(3) 总体分布的变异系数越大,正态单边容差上限估计的误差也就越大;

(4) 样本量越大,正态单边容差上限估计的误差越小。

3 基于正态单边容差方法的振动功率谱统计归纳误差与样本量的关系

根据正态单边容差上限的百分比误差公式,即可确定样本量与上限估计误差的关系。然而在工程应用中,受限于实测成本,很难获得大量的功率谱密度样本,所以很难获知功率谱密度值概率分布的总体变异系数。因此,需要对功率谱密度值的总体分布情况进行合理的假设。

根据正态分布的性质可知,呈正态分布的变量其值落在[ux-3σx,ux+3σx]的概率为0.997 3,所以,可认为ux-3σx是正态分布的最小值。同时,考虑到功率谱密度均为正值,因此有:

ux-3σx>0

(20)

即:

cv<1/3

(21)

因此有:

(22)

式(22)是基于正态分布的3σ原则的简化得到,存在大小不满足的情况,但这种情况的发生是小概率事件。因此式(22)对于确定正态单边容差上限估计误差的最大值有一定的指导意义。

不同总体分布变异系数的P95/50上限估计误差随样本量的变化曲线如图3所示,不同总体分布变异系数的P99/90上限估计误差随样本量的变化曲线如图4所示。

图3 不同变异系数的P95/50上限估计误差随样本量的变化曲线Fig.3 The curve of the P95/50 upper limit estimation error of different coefficients of variation as a function of sample size

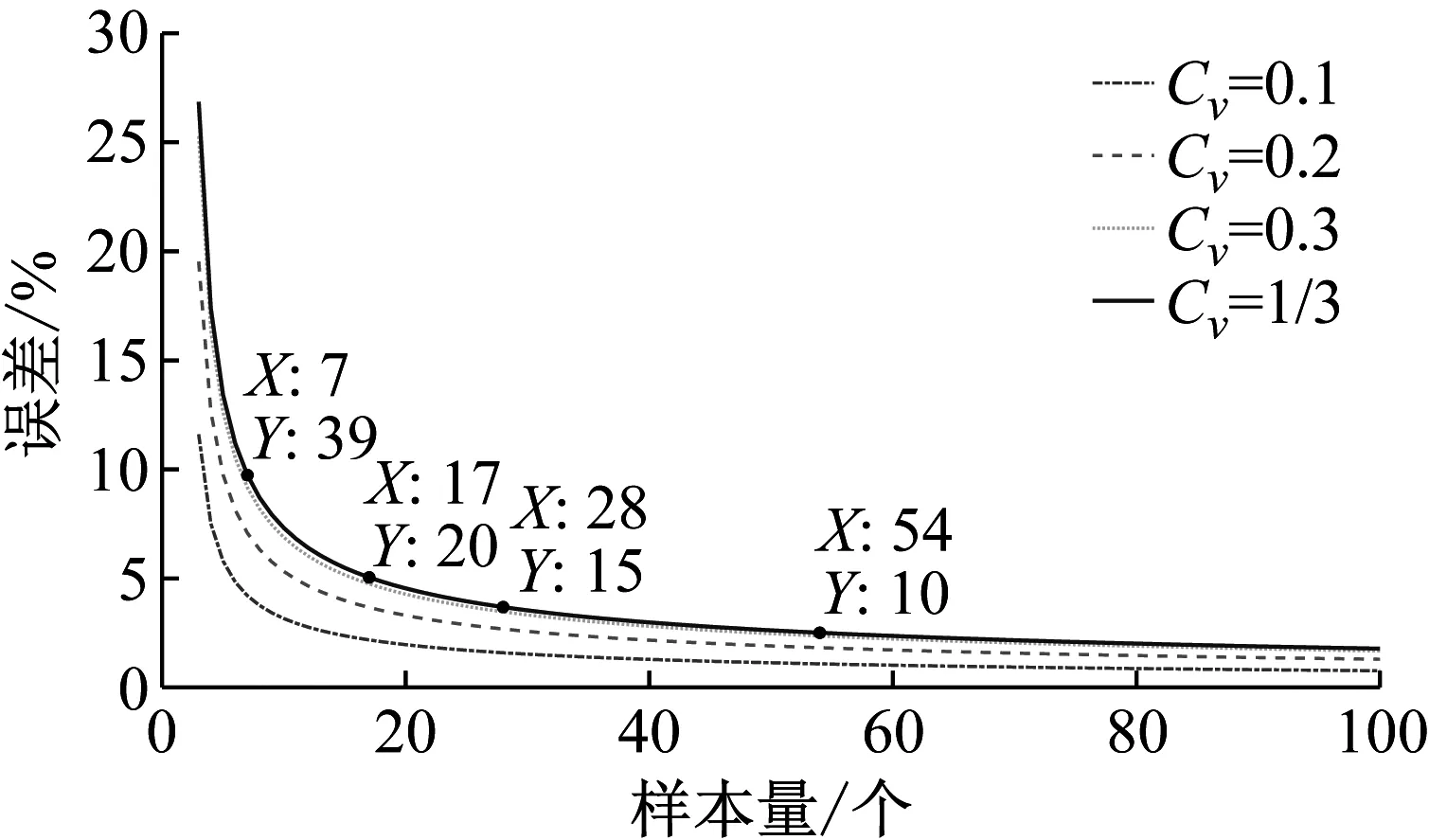
图4 不同变异系数的P99/90上限估计误差随样本量的变化曲线Fig.4 The curve of the P99/90 upper limit estimation error of different coefficients of variation as a function of sample size

从图3中可以看出:

(1) 5个样本可使P95/50上限估计的误差不超过20%;

(2) 9个样本可使P95/50上限估计的误差不超过15%;

(3) 20个样本可使P95/50上限估计的误差不超过10%;

(4) 70个样本可使P95/50上限估计的误差不超过5%。

从图4中可以看出:

(1) 7个样本可使P99/90上限估计的误差不超过40%;

(2) 17个样本可使P99/90上限估计的误差不超过20%;

(3) 28个样本可使P99/90上限估计的误差不超过15%;

(4) 54个样本可使P99/90上限估计的误差不超过10%。

4 小样本量振动功率谱统计归纳方法研究

通过前3章内容可以看出,当样本量较小时,采用正态单边容差上限方法进行振动功率谱统计归纳时误差较大,而Bootstrap法在小样本量统计归纳则具有一定优势,因此可对比正态单边容差上限法估计误差和自助容差上限法估计误差随样本量的变化关系。

自助容差上限估计的详细步骤如下:

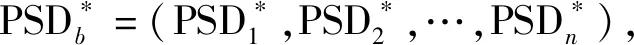
(5) 重复(3),(4)步N次,N≥1 000;

为了对比小样本下正态单边容差上限估计和自助容差上限估计误差,采用如下思路研究自助容差上限估计误差随样本量的变化关系:

(1) 给定正态总体的期望和标准差,生成一组呈正态分布的数据A,数据个数为1 000 000;

(2) 从A中随机挑选N个样本计算其自助容差上限xu(N,γ,β);

(4) 改变挑选的样本个数N,重复过程(2)～(3),得到不同样本数的自助容差上限估计的百分比误差。

假定某一带宽内的功率谱密度样本服从正态分布N(0.1,(1/30)2),采用自助容差上限方法分别计算覆盖概率为95%、置信度为50%的估计上限和覆盖概率为99%、置信度为90%的估计上限,并分别计算其百分比误差,并与变异系数为1/3的正态单边容差上限的百分比误差的理论解(式(22)的)对比,如图5和6所示。

图5 覆盖概率95%置信度50%的上限估计误差随样本量的变化曲线Fig.5 The curve of the Estimation error of upper tolerance limit with coverage probability of 95% and confidence of 50% versus sample size curve

从图5中和图6可以看出:

图6 覆盖概率99%置信度90%的上限估计误差随样本量的变化曲线Fig.6 The curve of the Estimation error of upper tolerance limit with coverage probability of 99% and confidence of 90% versus sample size curve

(1) 统计归纳覆盖概率为95%,置信度为50%的上限时,自助容差上限相比正态单边容差上限没有优势;

(2) 统计归纳覆盖概率为99%,置信度为90%的上限时,且当样本量小于20时,自助容差上限方法相比正态单边容差上限方法能明显降低估计上限的误差,而当样本量较大时,自助容差上限相比正态单边容差上限没有优势。

因此,当统计归纳小样本量(样本量小于20)覆盖概率为99%,置信度为90%的上限时,优先选用自助容差上限方法。

5 结 论

本文根据正态单边容差上限的定义,推导了正态单边容差上限估计的均方根误差和百分比误差的公式,并结合数值仿真结果,校验了公式的正确性。同时给出了振动功率谱密度P95/50和P99/90上限估计在不同样本量时的最大误差。最后,对比了正态单边容差上限和自助容差上限估计误差随样本量的变化关系。

本文得到以下结论:

(1) 正态单边容差上限的估计误差与样本个数和总体分布的变异系数相关;

(2) 正态单边容差上限的估计误差随样本量的增加而减小;

(3) 正态单边容差上限的估计误差随变异系数的增加而增加;

(4) 当样本量小于20时,统计归纳覆盖概率为99%、置信度为90%的上限时,自助容差上限估计误差明显小于正态单边容差上限方法。