高速柔性转子-非定心SFD系统响应特征分析与试验验证

2023-09-20唐振寰成晓鸣

振动与冲击 2023年17期

卢愈,唐振寰,成晓鸣,邓婷

(中国航发湖南动力机械研究所,湖南株洲 412000)

某型航空发动机动力涡轮转子为跨二阶临界转速工作的多支点、大长径比柔性转子系统,由于整机结构设计的空间限制,且转子系统需要在靠近临界的宽广转速范围内长时间变转速稳定运行,因此拟通过在转子支承处设置非定心挤压油膜阻尼器(squeeze film damper,SFD)实现预期目标[1]。与定心型挤压油膜阻尼器相比,非定心挤压油膜阻尼器结构更为简单紧凑,但是具有更强的非线性特征,而且在转子进动中必须考虑初始静偏心的影响[2];同时为了降低转子因较强的非线性而产生多频振动响应,从而导致结构疲劳破坏[3],工程设计中迫切需求开展转子-支承系统非线性动力学特征分析,进而设计合理的非定心挤压油膜间隙。

国家的税制改革中规定了配合国家住房制度的改革，即企业和行政事业单位如果按照房改成本价进行住房的出售人取得的收入将免征增值税。当前，我国在进行大中型林场的棚户区改革建设，如果建立千套住房，每套住房的成本价是45万元的话，千套住房实现降低税负4500万元，这是进行营改增之后为林场提供的福利政策，同时也使林场的职工更加热爱林业建设。因此可以说营改增的利好政策主要包括三点：政府进行财政补助的利好；银行给予贷款房屋的利好；税收部门进行税收减免的利好。

文献[4]研究了挤压油膜阻尼器转子的不平衡响应稳定性和分岔特征,发现挤压油膜阻尼器可能导致系统的非协调进动;文献[5-6]基于CFD方法分析了挤压油膜阻尼器中心槽、进油孔和进油压力对挤压油膜压力分布的影响,得到了理论上的最佳供油槽深度;文献[7]开展了静偏心对挤压油膜减振特性影响的理论推导,并基于Jeffcott转子开展了转子响应研究,发现静偏心显著影响转子系统的轴心轨迹;文献[8]设计了转子试验器,开展了静偏心对挤压油膜阻尼器减振特性影响的实验研究,发现静偏心较大时转子系统出现非协调进动,转子振动临界峰值出现波动;文献[9]推导了静偏心条件下挤压油膜阻尼器的油膜力表征公式,发现静偏心程度增加会导致转子系统临界转速增加及其对应幅值降低;文献[10]开展了转子-挤压油膜阻尼器减振效率的理论研究,并分析了较低转速下减振效果不佳的原因;文献[11]通过考虑挤压油膜阻尼器的非线性力,揭示了轴承共腔-双转子系统耦合振动的机理,并在转子试验和某型涡轴发动机整机试验中得到了验证。

本文针对某型航空发动机动力涡轮转子的结构特征建立了多支点柔性转子-非定心SFD系统动力学模型,通过模态综合法对转子有限元模型进行缩聚,在支承处考虑了转子自重下沉引起的挤压油膜静偏心,采用数值方法求解系统运动微分方程,结合转子系统不平衡响应、分岔图、庞家莱截面、频谱等特征,开展了不同挤压油膜间隙的转子系统动力学特性研究,提出了一种油膜间隙设计方法,并通过了转子试验验证,为航空发动机转子减振设计提供理论和技术支持。

1 转子系统建模

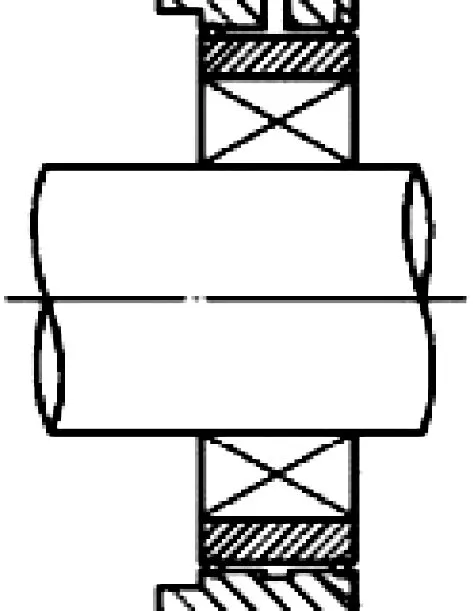
首先在ANSYS软件中采用基于Timoshenko梁理论的Beam189单元建立了某型航空发动机动力涡轮转子的有限元模型,并采用集中质量单元Mass21模拟叶片的集中质量和转动惯量,该转子共有4个支承,其中2#支点处采用了非定心SFD,其余3个支点为弹性支承,如图1所示。

图1 转子有限元模型Fig.1 Finite element model of rotor

1.1 运动微分方程

通过实验教学提高学生的动手能力和创新能力，这是改革实验教学的根本点和出发点。如果还是沿用母体学院的教学体系，对实验内容、实验方法按部就班地去完成，教学目标就很难实现。因为这些传统的实验内容大多是验证性实验，缺乏系统性和实用性，不能引导学生去解决实际工程中的问题，当然也谈不上培养学生的创造性思维能力。

(1)

与第1.2节的计算相比,可以发现本节的不平衡响应计算中,转子系统1阶临界的峰值并不明显,2阶临界存在多峰值现象,更为有效的描述了转子系统的响应特征。

通过加工和装配不同半径大小的2#支承轴承座,开展不同油膜间隙的动力涡轮模拟转子动力特性试验,试验前经过调整实测后油膜半径间隙与设计值0.05 mm、0.10 mm、0.15 mm保持一致。

综上所述，对于Hcy与Cys C的检测对于高血压早期肾损伤具备较高的特异性与灵活性，基于早期发现的高血压疾病患者我而言，肾功能损伤的具体程度显得极其重要，此外，早期治疗能够显著的降低患者治疗与预后产生的费用，在临床上非常值得推广应用。

(2)

(3)

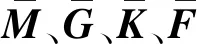
在图1所示的模型中,2#支点采用了非定心挤压油膜阻尼器支承,如图2所示。

(a)

采用固定界面模态综合法对模态子结构进行自由度缩减,具体步骤见文献[12]和[13],本文不再赘述,将内部自由度缩减至40个,以减小后续运动微分方程的数值求解计算量,因此将式(2)写成

(4)

式中:μ为滑油黏度;R为轴颈半径;L为SFD长度;c为油膜半径间隙;x、z分别为转子轴颈偏心在水平和垂直方向上的投影;I1、I2、I3为Sommerfeld积分,tanΨ=x/y。

读程学武的文章《纸糊的墙》（《杂文月刊》原创版2018年10月上），想到了游宇明的文章《“下地”的制度才叫制度》（《杂文月刊》原创版2018年7月上）。走进我们的办公室，各种规章制度挂满了墙。墙上的制度不叫制度，叫摆设，是专门给领导看的。下地的制度在工作人员心里，这才叫制度，是工作人员搞好工作的依据。制度要有操作性，不能原则上都正确，落实却无目标。切实可行的制度一定要下地，要落实。真正做到有制度必须执行，执行制度必须严格。

在本文的分析中,为了考虑静偏心的影响,计算了转子z方向的自重下沉量Δh,在式(4)的计算中,将偏心率ε的计算进行了修改。

分布式能源行业能效高、低排放、技术密集决定了其投资高，再加上承担园区供热管网建设，以及主要设备燃机属高端制造业，国产化进程有待时日，行业投资高于燃煤发电。

(5)

式中,Kx、Kz分别为水平和垂直方向上的弹性支承刚度。

将式(4)、式(5)代入式(3),采用Newmark-β法对非线性微分方程组进行求解,再将求解结果通过矩阵运算由模态空间转换到物理空间,即可得图1所示模型中各节点的动力学响应。

2014年1月17日，连任中国乒协主席；同年1月21日，当选为新一任中国足球协会主席；同年1月24日，连任中国羽毛球协会主席成功。

1.2 临界转速

该型航空发动机动力涡轮转子设计最高工作转速为17 000 r/min,慢车转速为3 500 r/min,变转速停留的工作范围为n～17 000 r/min(设计中期望n越低,则可变转速范围越大)。

基于图1的有限元模型,采用SAMCEF软件计算转子系统临界转速,当2#支点的刚度不同时,临界转速计算结果如表1所示。

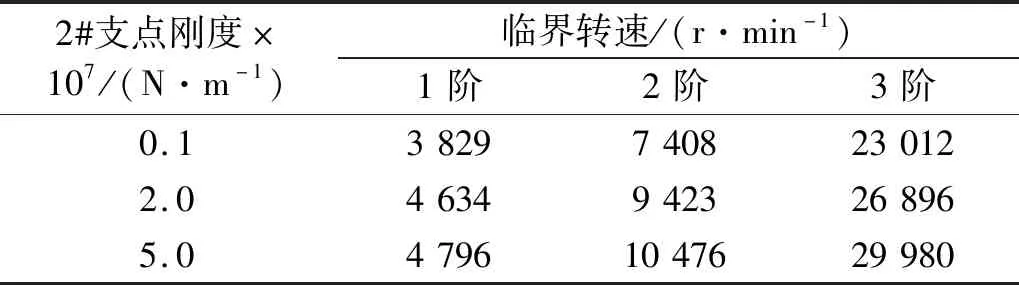
表1 转子系统临界转速Tab.1 Critical speed of the rotor system

多维尺度分析是基于数据空间距离来探索观察量的内在结构，以二维(三维)空间居多，将观察量以点分布的形式描述其在空间所处位置。不同观察量所呈现点的位置的空间距离远近代表了其相似性的高低。相似度越高的关键词越易聚拢形成学科热点。同时，越靠拢中心位置的关键词表明其中介中心性越强，与其相联系的关键词越多，其越处于所在研究的核心位置；反之则越少，越处于边缘。以22个高频关键词所构建的相异系数矩阵导至SPSS 21.0进行多维尺度分析(结果如图4)，设置标准Z分数，拟合参数值如下：Stress=0.24，RSQ=0.63。说明高频词间拟合度有待提升。

(6)

因此,2#支点刚度太小则1阶临界转速与慢车转速的裕度不足,2#支点刚度太大则可变转速范围减小。而由于2#支点为非定心SFD,其支承刚度随转速、偏心率等变化,因此采用传统有限元方法而不考虑支承刚度变化的临界转速计算与实际值存在较大误差。本文基于转子系统非线性特征分析,结合模拟转子试验,更为准确的计算了转子系统响应,验证了通过选择合适的油膜间隙,在保证具有一定裕度的情况下能够使转子系统在9 000～17 000 r/min的范围内实现长时稳定的变转速运行,从而实现工程设计目标。

2 转子系统响应特征

对于大长径比且跨临界转速工作的动力涡轮转子,其转子轴中点处的位移响应是工程设计中评判转子动力特性的一个重要依据,下文将开展图1所示转子模型的轴中点处竖直方向响应特征分析,为油膜间隙设计提供仿真计算基础。

2.1 非线性动力学特性

为了研究油膜间隙变化对转子系统非线性响应特征的影响,在转子系统2#支承处分别选择了0.05 mm、0.1 mm和0.15 mm三种不同的油膜间隙值,其他三个支承处刚度阻尼保持不变,通过求解方程(3)可得转子系统的响应,其不同油膜间隙下的响应分岔图如图3、图4和图5所示,图中纵坐标反映了转子轴中点位移响应的单峰值。

图3 转子系统分岔图(c=0.05 mm)Fig.3 Bifurcation diagram(c=0.05 mm)

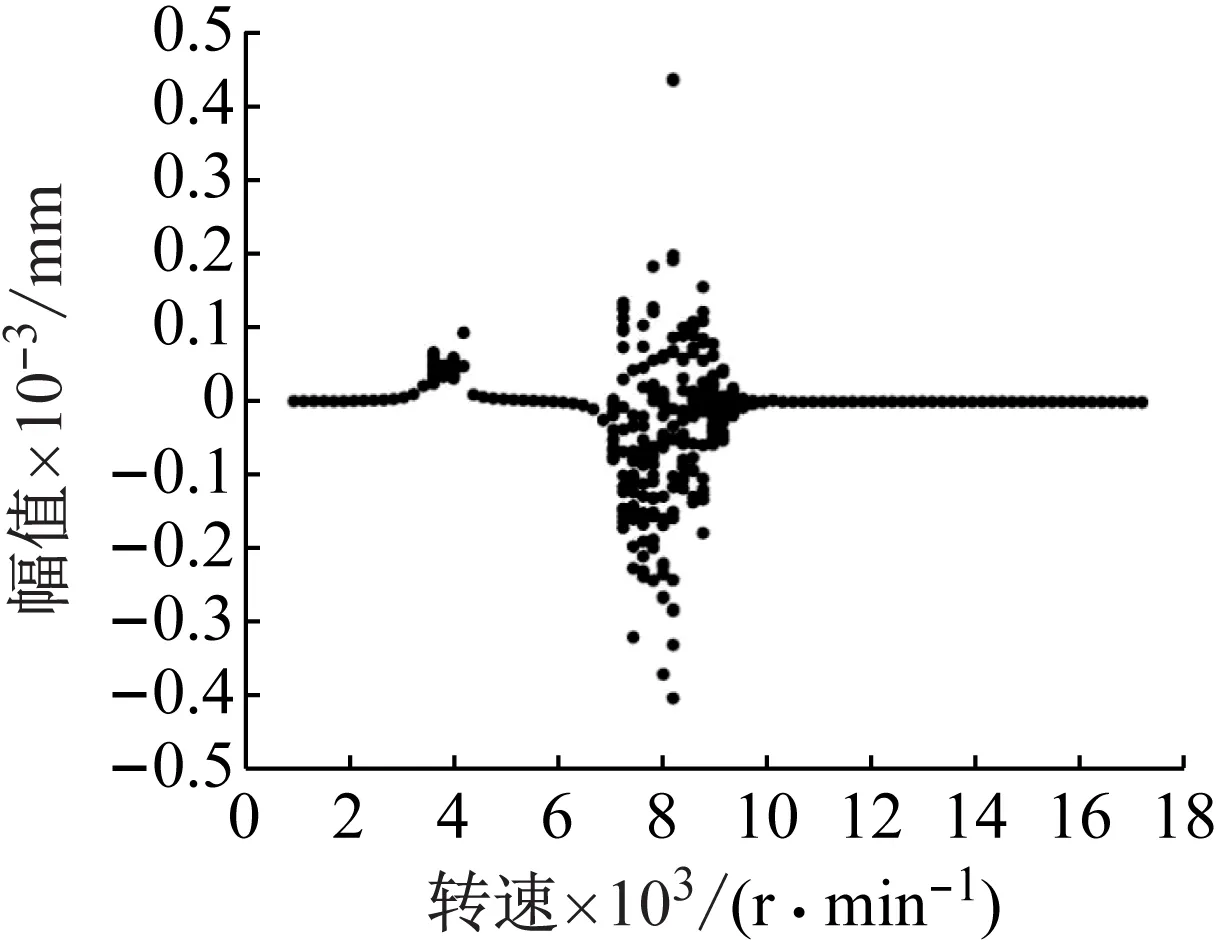
图4 转子系统分岔图(c=0.1 mm)Fig.4 Bifurcation diagram(c=0.1 mm)

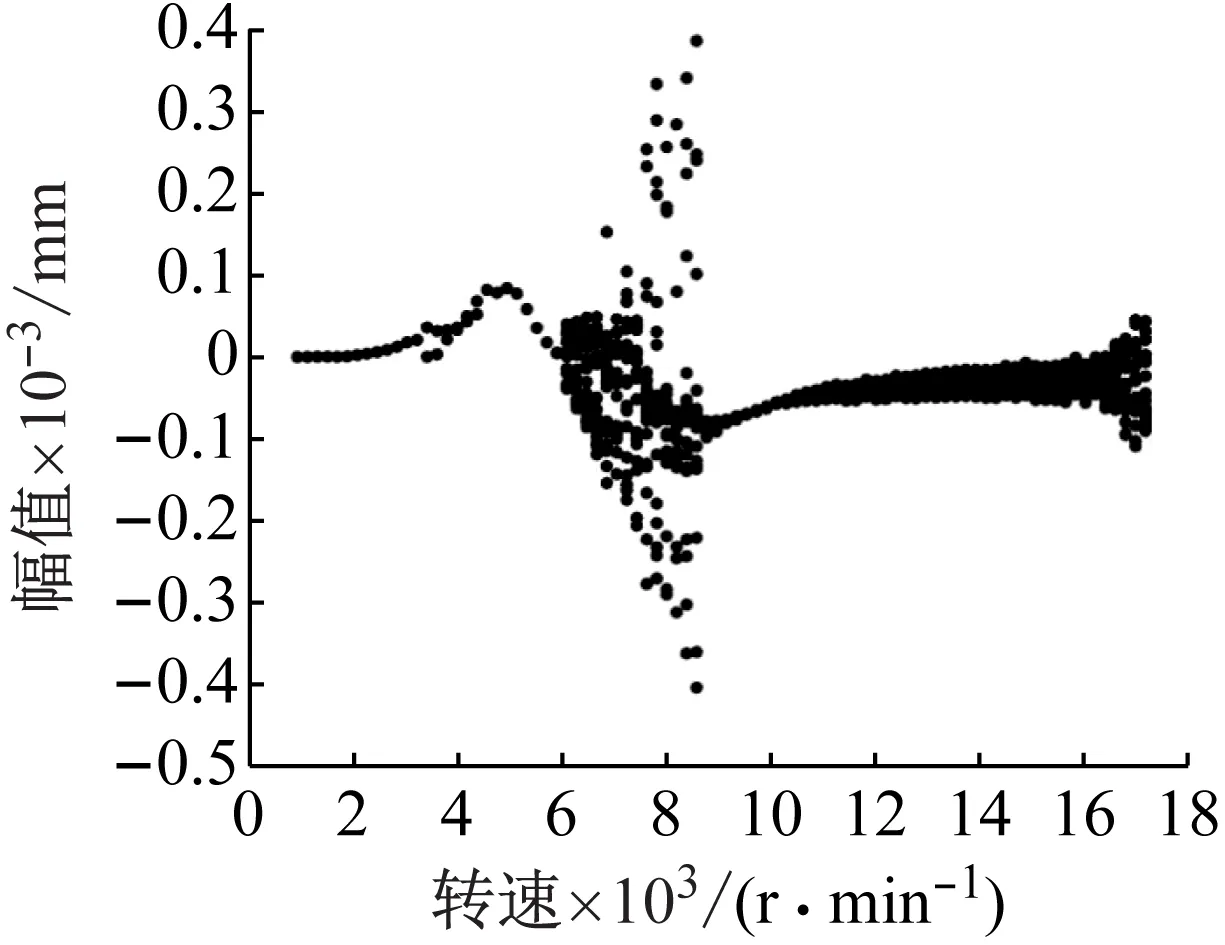
图5 转子系统分岔图(c=0.15 mm)Fig.5 Bifurcation diagram(c=0.15 mm)

对比图3～图5,可以发现由于非定心SFD的存在,转子系统响应具有明显的非线性特征,不同油膜间隙下其分岔图变化规律大体相似,均为在较低转速下转子为“单周期运动”,而后经过一次较短的分岔又回归到“单周期运动”,然后又经过倍周期分岔逐步进入“多倍周期运动”、“拟周期运动”或“混沌运动”,最后又逐渐回归“单周期运动”。而且油膜间隙的不同,明显导致了响应分岔点发生改变,“多倍周期运动”、“拟周期运动”或“混沌运动”等区域的转速范围存在较大差异[15]。

当油膜间隙较大(c=0.15 mm)时,与相对较小间隙时(c=0.1 mm)相比,在高转速下回归“单周期运动”后存在一定的发散和再次分岔,且频谱上存在更多的频率成分,其中不同油膜间隙下17 000 r/min转速的庞加莱截面和频谱如图6和图7所示。

在一般的设计规范中,转子临界转速与工作转速之间需满足20%的裕度,即:

(a) 庞家莱截面

为了使转子系统在高转速下长时间运行,避免因强非线性而造成动力特性较差,产生多频振动响应,影响转子系统长时间使用寿命[16],根据本节的仿真分析,非定心油膜间隙不宜太大。

2.2 不平衡响应特征

当非定心挤压油膜间隙变化时,转子轴中点处不平衡响应如图8所示(为与后续试验结果进行对比,图8中纵坐标为位移响应的有效值)。当油膜半径间隙为0.05 mm时,响应峰值为0.95 mm左右,对应的峰值转速在11 500 r/min附近;当油膜半径间隙为0.10 mm时,响应峰值为0.36 mm左右,对应的峰值转速在7 800 r/min附近;当油膜半径间隙为0.15 mm时,响应峰值为0.31 mm左右,对应的峰值转速在8 600 r/min附近。

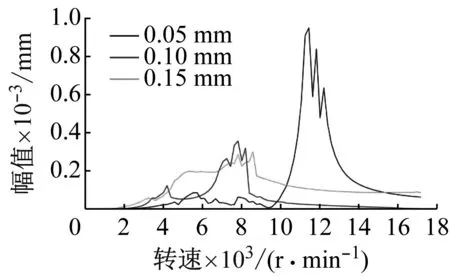
图8 转子中点处不平衡响应Fig.8 Unbalanced response at the midpoint of rotor

式中:M、G和K分别为转子系统质量矩阵、陀螺矩阵和刚度矩阵;Fe和FF分别为外部作用力(本文中为不平衡力和重力)和支承处作用力;u为位移向量。转子有限元模型有n=3 641个节点,则M、G、K维度为4n×4n,Fe、FF和u维度为4n×1。

（2）Mann-Kendall分析为非参数统计检验方法［4-5］。假设水文序列Xt无显著变化趋势，其标准化统计量为U，给定置信度α，若|U|＞Uα/2，存在显著变化趋势；反之，无显著变化趋势。其中，U为正值，呈上升趋势；反之，呈下降趋势。

可以发现当油膜半径间隙为0.05 mm时转子系统响应峰值和对应的转速显著增大,此时转子在峰值处将产生较大的载荷,不利于转子减振;且工程设计中要求转子系统拥有尽量大的变转速工作范围,若峰值转速过大,将导致转子变转速范围缩小;因此非定心挤压油膜间隙不宜太小。而且过响应峰值后的高转速下,当油膜半径间隙为0.15 mm时不平衡响应位移较大,与前文的非线性动力动力学特性相吻合。

2.3 对比分析

综合对比不同油膜间隙下,多支点柔性转子-非定心SFD系统非线性动力学特性和不平衡响应特征:当非定心挤压油膜间隙较小时,将导致转子系统不平衡响应峰值和对应的转速较大,不利于转子系统扩大工作转速范围;而当非定心挤压油膜间隙较大时,将导致转子系统具有更强的非线性特性,转子在高转速运行时产生复杂的多频振动响应,且过峰值后不平衡响应更大。为了满足工程设计中转子系统在更宽广的转速范围内长时间变转速稳定运行需求,由仿真模拟结果可知,当2#支承处的油膜半径间隙为0.1 mm时,转子系统峰值响应较小,具有较大的工作转速范围,且过峰值后不平衡响应较小。

3 转子系统试验

3.1 试验器设计

为了验证数值仿真结果,基于图1和图2的高速多支点柔性转子-非定心SFD系统,设计了动力涡轮模拟转子系统试验器,如图9所示。动力涡轮模拟转子主要由动力涡轮轴和动力涡轮一、二级模拟盘组成(为了避免气动力造成的影响,以模拟盘代替真实涡轮盘和叶片,确保模拟盘质心、质量、转动惯量等与真实叶片盘保持一致),整个转子共有4个支点,其中2#支承为非定心挤压油膜,其他支承为鼠笼弹性支承。

忽略转子的轴向运动,考虑陀螺力矩,且将各支承处的作用力和不平衡力作为外力,则转子运动方程可写为

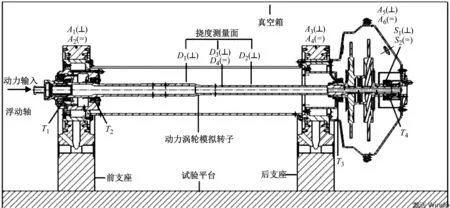
(a) 试验设计

以I表示内部自由度,以J表示界面物理自由度,则式(1)可写成

3.2 测试参数

动力涡轮模拟转子试验件前端与高速电机输入端通过浮动轴相连,试验中高速电机从0逐渐加速至17 500 r/min,试验期间供油压力为0.4～0.9 MPa,测量参数如表2所示。

表2 动力涡轮转子试验测试参数Tab.2 Power turbine rotor experiment test parameters

3.3 试验结果

表2中支座加速度、轴承温度、弹支应变测量主要为了保证转子试验的安全性,对于2#支承处不同油膜间隙的动力涡轮轴中点位移(RMS值即有效值)随转速变化的测量结果如图10所示。

(a) D1测点位移

3.4 仿真与试验对比

对比图8与图10,其中D3点为动力涡轮轴中点竖直方向的位移响应,可以发现理论与试验的转子系统在不同油膜间隙下不平衡响应变化规律相似;当油膜半径间隙为0.05 mm时,转子的响应峰值和对应转速较大;当油膜半径间隙为0.15 mm时,转子过峰值后位移响应较大;当油膜半径间隙为0.10 mm时,转子响应峰值较小且可工作转速范围较大,与第2章中系统响应特征的结论相吻合。上述结果验证了本文转子-非定心SFD非线性动力学模型的有效性,证明了2#支承处非定心油膜半径间隙取0.10 mm的合理性。

(3)中心度(centrality)：中心度用以衡量各节点在旅游经济网络中是否居于中心的地位，主要有3种表现形式：程度中心度、接近中心度和中介中心度[24]。程度中心度用来测量各城市节点的旅游经济交往能力，度数越高，该节点拥有的权利越大。接近中心度用来测量一个节点与其他节点的旅游经济往来的便利性，用一个节点与其他所有节点的捷径距离之和表示。中介中心度反映各节点在多大程度上位于其他节点交往路线的“中间”地位，并控制其他节点的交往能力。其值越高，控制力就越强，在旅游经济网络中就越具有垄断性地位。

本着分级回收的原则，对主厂房现有煤泥回收设备进行完善，淘汰原有3台SB6400筛网沉降离心机，更换2台唐山森普离心机和2台博润离心机，处理能力达到100 t/h以上，大幅度降低了洗水中的煤泥含量，一段浓缩机沉降效果明显加强。