三角代数上的局部广义李n导子

袁 鹤，俞慧玲，田 莹

(吉林师范大学 数学学院，吉林 四平 136000)

1 预备知识

设R是含有单位元的交换环，A和B是R上含有单位元的代数，设M是非零(A,B)-双模且既是左A-忠实模又是右B-忠实模，定义集合

容易看出，πA(Z(T))是Z(A)的子代数，πB(Z(T))是Z(B)的子代数，且存在唯一的代数同构τ:πA(Z(T))→πB(Z(T))，满足对于任意的a∈πA(Z(T)),m∈M，有am=mτ(a)[1].

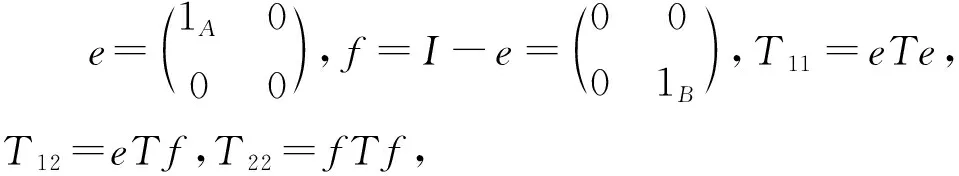
本文提到的线性映射均为R-线性映射.若代数T上线性映射d:T→T满足d(xy)=d(x)y+xd(y),x,y∈T，则称d为导子.若对于线性映射g:T→T，存在导子d:T→T满足g(xy)=g(x)y+xd(y),x,y∈T，则称g为广义导子，并称d为g的伴随导子.类似地，可以给出李导子及广义李导子的定义.

若线性映射θ:T→T满足

θ([x,y])=[θ(x),y]+[x,θ(y)],x,y∈T,

则称θ为李导子.若对于线性映射φ:T→T，存在李导子θ:T→T，满足

φ([x,y])=[φ(x),y]+[x,θ(y)],x,y∈T,

则称φ为广义李导子，并称θ为φ的伴随李导子.相应地，可以定义李n导子及广义李n导子.

设

若线性映射L:T→T满足

则称L为李n导子.同样地，若对于线性映射G:T→T，存在李n导子L:T→T满足：对于任意的x1,x2,…,xn∈T，有

则称G为广义李n导子，并称L为G的伴随李n导子.

2 主要结果

若对于线性映射δ:T→T及任意的x∈T，存在广义李n导子Gx:T→T满足δ(x)=Gx(x)，则称δ为局部广义李n导子.

由引理1知，只需研究三角代数上满足eG(f)f=0的广义李n导子的表达式便可以得到一般的广义李n导子的表达式.因此，假设本文的局部广义李n导子δ满足：对于任意的x∈T，存在T上满足eGx(f)f=0上的广义李n导子Gx，使得

δ(x)=Gx(x).

(1)

( i )eZ(T)e=Z(T11),fZ(T)f=Z(T22);

(ii)Z(A)={a:[[a,x],y]=0,∀x,y∈A}或Z(B)={b:[[b,x],y]=0,∀x,y∈B}.

则T上广义李n导子G可以表示成G(x)=g(x)+τ(x),x∈T，其中g:T→T为广义导子，τ:T→Z(T)满足τ(pn(x1,x2,…,xn))=0,∀x1,x2,…,xn∈T.

( i )A,B可由其中的幂等元生成;

(ii)eZ(T)e=Z(T11),fZ(T)f=Z(T22);

(iii)Z(A)={a:[[a,x],y]=0,∀x,y∈A}或Z(B)={b:[[b,x],y]=0,∀x,y∈B}.

则T上满足(1)的局部广义李n导子δ可以表示成δ(x)=G(x)+h(x),n≥2，其中G:T→T为广义导子，h:T→Z(T)满足h(pn(x1,x2,…,xn))=0,∀x,x1,…,xn∈T.

根据文献[8]引理2.2，结合引理3可得

其中P⊥=I-P,Q⊥=I-Q,τi满足τi(pn(x1,…,xn))=0,i∈{1,2,3,4},x1,…,xn∈T.

证明对于任意的A12∈T12，由A12=pn(A12,f,…,f)及引理2可得

其中DA12为广义李n导子GA12的伴随李n导子.上式两边左乘e右乘f，可得e[A12,DA12(f)]f=0，因此δ(A12)=eδ(A12)f.】

引理6在定理1的假设条件下，局部广义李n导子δ满足：对于任意的A11∈T11,A22∈T22，有fδ(A11)f∈Z(T22),eδ(A22)e∈Z(T11).

证明对于任意的A11∈T11,A22∈T22,A12∈T12，由pn(A11,A22,A12,f,…,f)=0可得

其中DA11为GA11的伴随李n导子，因此

即

因此，对于任意的A11∈T11,A22∈T22，有f[GA11(A11),A22]f=[fGA11(A11)f,A22]∈Z(T22)，由定理1的(iii)有fGA11(A11)f∈Z(T22)，即fδ(A11)f∈Z(T22).显然n=2时上式仍成立.

同理可得eδ(A22)e∈Z(T11).】

根据引理6，定义f1(A11)=fδ(A11)f∈Z(T22),f2(A22)=eδ(A22)e∈Z(T11)，则对于任意的x1,x2,…,xn∈T11，有

其中Dpn为Gpn的伴随李n导子.类似地，对于任意的y1,y2,…,yn∈T22有f2(pn(y1,y2,…,yn))=0.再定义h(x)=f1(exe)+η-1(f1(exe))+f2(fxf)+η(f2(fxf))，其中x∈T并且η为预备知识中的代数同构，则

令

G=δ-h.

(4)

由引理5及h(A12)=h(pn(A11,A12,f,…,f))=0可知，对任意的A12∈T12,A11∈T11,A22∈T22，有

显然，对于任意的广义导子g:T→T，有

事实上，一方面，对于任意的A11∈T11,A12∈T12，有

另一方面，对于任意的A12∈T12,A22∈T22，有

比较上面两式可得g(A12)∈T12.同时，对于任意的A11∈T11,A22∈T22，有

引理7在定理1的假设条件下，满足(4)式的G为广义导子，其伴随导子为d(x)=G(x)-G(I)x,x∈T.

证明首先证明对于任意的A11∈T11,A22∈T22,A12∈T12，有

其中d(x)=G(x)-G(I)x.

由于T上存在满足eGA11B11(f)f=0的广义李n导子GA11B11，使得GA11B11(A11B11)=δ(A11B11)，所以由文献[7]引理3.5可得δ(A11B11)∈T11+T22.根据文献[8]引理2.5、本文引理5及(8)～(12)式，有

上式两边左乘e右乘f，则由δ(A11B11)∈T11+T22及引理5，有

将δ=G+h代入得到

令B11=e，则

下证对于任意的A11∈T11,A12∈T12，有

由(16)式可知，当n=1时上式成立.设

于是结合(15)式可得

同理，对于任意的A12∈T12,A22∈T22，有

令d(x)=G(x)-G(I)x,x∈T，则d(A11A12)=d(A11)A12+A11d(A12).事实上，由(6),(7)及(17)式，有

其次，证明对于任意的A11,B11∈T11,A22,B22∈T22，有

一方面，对于任意的A11,B11∈T11,A12∈T12，有

另一方面，由(18)式可得

比较上面两式，则有

(G(A11B11)-G(A11)B11-A11d(B11))A12=0.

由T12的忠实性可得

G(A11B11)=G(A11)B11+A11d(B11).

类似地，一方面，对于任意的A12∈T12,A22,B22∈T22，有

另一方面，

比较上面两式，有

由T12的忠实性可得

G(A22B22)=G(A22)B22+A22d(B22).

最后，类似于(18)式的证明过程可得d为导子.】

定理1的证明由(3)及(4)式可知δ=G+h，其中h:T→Z(T)满足：对于任意的x1,x2,…,xn∈T，有h(pn(x1,x2,…,xn))=0.再由引理7知，G为广义导子.】