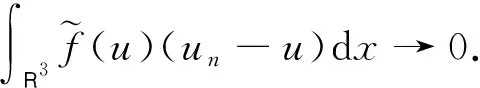一类薛定谔-泊松系统多重解的存在性
2023-09-19胡天群陈林松
胡天群,陈林松,周 鉴*
(贵州师范大学 数学科学学院,贵州 贵阳 550025)
多重解的存在性,其中位势函数V(x)是可变号的.当f和V满足适当条件时,利用变分法和Morse理论得到了该系统多个非平凡解的存在性.
0 引言
研究R3中的薛定谔-泊松系统

(1)
系统(1)由Bench等[1]首次提到,用来描述非线性稳态的薛定谔方程与静电场之间的相互作用,它广泛出现在量子力学模型和半导体理论[2-6].
2007年,Wang等[7]首次研究了具有不定位势的薛定谔-泊松系统,其中f是渐近线性的.Chen等[8]假设非线性项f是4-超线性的,通过局部环绕定理和喷泉定理,得到了系统(1)至少一个解和无穷多个解的存在性.Liu等[9]通过Morse理论也研究了f是4-超线性的情况,Alves等[10]利用形变引理和Miranda定理得到了系统(1)的一个变号解.当f为3次线性和非线性时,Liu等[11]研究了系统(1)的非平凡解的存在性.Lin等[12]研究了系统(1)的基态解的存在性,其中V(x)弱可微且渐近趋于常数.
以下假设以下条件成立:
(V)V∈C(R3)是下方有界的,且对任意实数G>0,有μ(V-1(-∞,G])<∞,这里μ表示R3上的Lebesgue测度;
(F1)f∈C(R3×R)且存在p∈(2,6),C>0,使得对任意的(x,t)∈R3×R,有
f(x,t)≤C(1+|t|p-1);

(F3)存在0 (F4)f关于变量t是奇函数,即f(x,-t)=-f(x,t). 众所周知,系统(1)具有变分结构,其解是H1(R3)×D1,2(R3)上泛函 的临界点问题,其中φu为泊松方程 -Δφ=u2 (3) 在H1(R3)中的唯一解.由文献[13]的定理2.2.1可知 (4) 首先介绍Schrödinger算子-Δ+V的特征值问题.考虑以下由极小极大值定义的递增序列λ1≤λ2≤…≤λn, (5) 如果λ∞是有限的,则λ∞是-Δ+V本质谱的底,并且对于任意的n∈N,不等式λn<λ∞意味着λn是有限重的特征值[14-15].如果V是下方有界的,则λn有定义且有限. 本文考虑系统(1)的多重解的存在性,得到如下主要结果: 定理1设条件(V)及(F1)~(F3)成立.若存在k≥1使得0∈(λk,λk+1),则系统(1)至少具有两个非平凡解. 定理2设条件(V)及(F1)~(F4)成立.若存在k≥1使得0∈(λk,λk+1),则系统(1)至少具有k对非平凡解. 需要指出的是,运用山路引理、喷泉定理、环绕定理、变分法等[7,8]来研究系统(1)时,通常对f做一些合适的假设(例如(AR)条件和当|u|→∞时F(x,u)/u4→+∞).然而,本文假设位势函数是可变号的,非线性项f是渐进线性的,没有(AR)条件和当|u|→∞时F(x,u)/u4→+∞,因此方法与前述文献有很大不同.本文对位势函数分区域进行讨论,利用Morse理论得到系统(1)的多重解的存在性,相比经典的变分法更直接. 由于V是下方有界的,所以可以选择m>2,使得对任意的x∈R3有 (6) 令 为H1(R3)的一个线性子空间,对任意的u,v∈E,定义 |u|s≤τs||u||, ∀u∈E, (7) 这里|·|s为Ls(R3)范数. 命题1[17]存在正常数a>0,对任意的u∈E,有 (8) 众所周知,在条件(F1)与(F2)下,泛函Φ属于C1(E,R),且对任意的u,v∈E,其导数为 Φ的临界点即为系统(1)的解. 下面回忆一些抽象的临界点理论.令X为Banach空间,Φ∈C1(X,R).设u是Φ的一个孤立临界点,Φ(u)=c,则Φ在u处的第q阶临界群定义为 Cq(Φ,u)=Hq(Φc,Φc{u}), 其中Φc:={u∈X:Φ(u)≤c},Hq(X,Y)是Z上拓扑对(X,Y)的第q阶奇异同调群.称Φ对于空间分解X=X-⊕X+在0处有一个局部环绕:若存在ρ>0使得 命题2[18]设Φ∈C1(X,R).若Φ对于空间分解X=X-⊕X+在0处有一个局部环绕,则0为Φ的一个临界点,且Cl(Φ,0)0,其中l=dimX-<∞. 定理A[19]设Φ∈C1(X,R)满足(PS)条件且Φ是下方有界的,若存在k≠0使得Ck(Φ,0)0,则Φ至少具有三个临界点. 定理B[20]设偶泛函Φ∈C1(X,R)满足(PS)条件且是下方有界的,如果Φ(0)=0,且存在集合K⊂X使得K通过奇映射与Sj-1同胚,则Φ至少具有j对不同的临界点,这里Sj-1表示j维单位球面,且supKΦ<0. 引理1对任意的u∈H1(R3),有不等式 证明由于φu是方程(3)的唯一解,所以 另一方面,可以推出 由此可见 引理2设条件(V),(F3)成立,则Φ是强制的,即当||u||→+∞时Φ(u)→+∞. 由条件(F3)可得 对任意的u∈E,有 因此只需证明Λ是下方有界的. 由(6)式可知V(x)≥-m,所以对任意的M>m+2h,x∈R3,有 故 相应地,将剩下的积分全部拆分到两个集合{V>M}和{V≤M}上,分明证明相应量的有界性. 条件(V)意味着{V≤M}具有有限测度.所以,应用Hölder不等式得到 因此 对于选择的M,m,上式右边显然是下方有界的. 考虑 为了验证能量泛函Φ满足(PS)条件,令 并将Φ改写成以下形式: 引理3设条件(V)与(F1)~(F3)成立,则泛函Φ满足(PS)条件,即任何满足supnΦ(un)<∞且Φ′(un)→0的(PS)序列{un)⊂E均存在收敛的子列. 由(9)和(16)式可知 通过文献[21]的引理2.3及un⇀u于E可知,当n→∞时,有 由条件(F1)和(F2)可知,对任意的C0>0,存在C1>0使得 通过(7)式及un⇀u于E,有 结合(17),(18)与(20)式可知||un-u||→0.】 引理4设条件(V),(F1),(F2)成立,则泛函Φ对于空间分解E=E-⊕E+在0处有一个局部环绕. 证明由于0∈(λk,λk+1).令E-=span{φ1,…,φk},E+=(E-)⊥,那么E-和E+是二次型Q(u)的负空间和正空间,其中 另外,dimE-=k<∞,且存在κ>0使得 ±Q(u)≥κ||u||2,u∈E±. (21) 由条件(F1)和(F2)可知,存在常数Cτ>0使得 若u∈E-,则由(7),(21)和(22)式,有 类似地,若u∈E+,则有 由于p>2,所以可选取充分小的ρ>0,使得:当u∈E-且||u||≤ρ时Φ(u)≤0;当u∈E+且0<||u||≤ρ时Φ(u)>0.】 定理1的证明根据引理2和引理3,Φ是强制的且满足(PS)条件,因此Φ是下方有界的.由引理4和命题2可知,Ck(Φ,0)0,其中k:=dimE-.由定理A可知,Φ至少有三个临界点.因此,系统(1)至少存在两个非平凡解. 定理2的证明由前面的讨论可知,Φ是下方有界的且满足(PS)条件.又由条件(F4)可知Φ为偶泛函.此外,对任意的ρ>0,令 Sρ={u∈E-:||u||=ρ}. 则由(23)式可知,存在足够小的正数ρ使得 由定理B可知,Φ至少有k对不同的非平凡临界点.】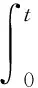



1 准备工作
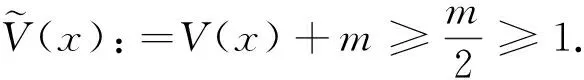

2 主要结果的证明