次线性算子的多线性交换子在变指标Herz型空间的有界性
2023-09-19张婉婧
张 婧,程 鑫,张婉婧
(1.伊犁师范大学 数学与统计学院,新疆 伊宁 835000;2.伊犁师范大学 应用数学研究所,新疆 伊宁 835000)
0 引言与主要结果
设f∈L1(Rn)具有紧支集,对∀x∉supp(f),T是次线性算子,定义
设b=(b1,b2,…,bm),bl∈BMO(Rn),l∈{1,2,…,m},m∈N,x∉supp(f),由次线性算子T与BMO(Rn)函数b生成的多线性交换子Tb定义为
其中K(x,y)是T的核函数.当m=1时,该算子为一阶交换子Tbf(x);当bl=b(1≤l≤m)时,该算子为m阶交换子.
近年来,随着对变指标函数空间的深入探讨,有关次线性算子及其交换子在变指标Herz型空间上的有界性引起了学者的关注.2010年,Izuki[1]建立了次线性算子在变指标Herz空间的有界性结果.近来,Wang等[2]证明了次线性算子从变指标Herz-Hardy空间到变指标Herz空间是有界的;王洪彬[3]证明了次线性算子一阶交换子在上述空间的有界性;程星星等[4-5]讨论了次线性算子和次线性算子的交换子的有界性;王盛荣等[6]建立了次线性算子在变指标Herz空间的加权有界性.
在变指标函数空间理论研究中,WANG等[7]证明了Littlewood-Paley算子的多线性交换子在变指标Lebesgue空间的有界性;赵欢等[8]建立了多线性Calderón-Zygmund算子与BMO(Rn)函数生成的多线性交换子在变指标Herz-Hardy空间的有界性.基于上述结果,本文考虑次线性算子与BMO(Rn)函数生成的多线性交换子在加权变指标Herz-Morrey空间和Herz-Hardy空间的有界性.
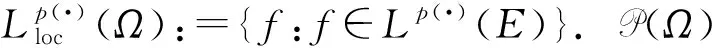
用B(Rn)表示满足p(·)∈P(Rn)且使得Hardy-Littlewood极大算子M在Lp(·)(Rn)上有界的函数p(·)的全体.
本文主要结果如下:
定理1设q(·)∈P(Rn),ωq(·)∈Aq(·),0 ( i )当k∈Z,supp(f)⊆Ak且|x|≥2k+1时,T满足尺寸条件 |Tf(x)|≤C||f||L1(Rn)/|x|n. (1) (ii)当k∈Z, supp(f)⊆Ak且|x|≤2k-2时,T满足尺寸条件 |Tf(x)|≤C2-kn||f||L1(Rn). (2) dist(x,suppf)≥|x|/2. 注2当b1=b2=…=bm=b时, 即交换子Tb为m阶交换子.所以定理1和定理2对m阶交换子的结论也成立. 当k∈Z时,令球 赋予如下范数: 则Lp(·)(Ω)是Banach空间,称为变指标Lebesgue空间. 引理1[2]设p(·)∈B(Rn),0<δ1,δ2<1,则存在正常数C,使得对所有Rn中的球B和所有可测子集S⊂B,都有 引理2[9]设p(·)∈P(Rn),若f∈Lp(·)(Rn),g∈Lp′(·)(Rn),则fg在Rn上可积,并且 其中rp=1+1/p--1/p+.不等式(4)称为相关于变指标Lp(Rn)空间的广义的Hölder不等式. 文献[14]定义的Muckenhoupt权函数Ap(p∈(1,∞))可以推广到变指标情形. 定义4[11]若q(·)∈P(Rn),且ω(x)是Rn上非负局部可积函数,则满足fω∈Lq(·)(Rn)的全体复值可测函数的集合为加权变指标Lebesgue空间Lq(·)(Rn,ω),记为Lq(·)(ωq(·)),其范数定义为||f||Lq(·)(ωq(·))=||fω||Lq(·). 由文献[11]的注1,Lq(·)(ωq(·))的对偶空间为Lq′(·)(ω-q′(·)),这里Lq′(·)(ω-q′(·))=Lq′(·)(Rn,ω-1). 引理3[11]若Hardy-Littlewood极大算子M在对偶空间Lq′(·)(ω-q′(·))上是有界的,则存在常数δ∈(0,1)和C>0,使得对所有Rn中的球B和所有可测子集S⊂B,都有 引理4[10,11]设q(·)∈B(Rn),则存在常数C>0,使得对所有Rn中的球B,有 定义5[2]设α∈R,0 其中 非齐次变指标Herz空间定义为 其中 定义6[13]设α∈R,0≤λ<∞,0 其中 非齐次加权变指标Herz-Morrey空间定义为 其中 其中N>n+1且 φ*是非切向极大算子,即 其中φt(x)=t-nφ(x/t). 定义7[2]设α∈R,0 ( i )齐次变指标Herz-Hardy空间定义为 (ii)非齐次变指标Herz-Hardy空间定义为 定义8[2]令nδ2≤α<∞,q(·)∈P(Rn)且非负整数s≥[α-nδ2], (a)Rn上的函数a称为中心(α,q(·))原子,如果它满足下列条件: ( i )对某个r>0,suppa⊂B(0,r)={x∈Rn:|x| (ii)||a||Lq(·)(Rn)≤|B(0,r)|-α/n. (b)Rn上的函数a称为限制型中心(α,q(·))原子,如果它满足条件(ii),(iii)及下列条件: (i′)对某个r≥1有suppa⊂B(0,r). 引理5[2]令nδ≤α<∞,0 (i),(ii)中的下确界是对f的所有上述分解而取的. BMO(Rn)空间是由满足如下条件的所有局部可积函数f构成的函数类: 特别地, 为了证明主要结果,首先建立如下引理,它是文献[10,11]中相应结果的推广. 引理6若m∈N,k>i(i,k∈Z),bl∈BMO(Rn),1≤l≤m,ωq(·)∈A1,则 这里上确界取遍Rn上的所有球B. 证明由广义Hölder不等式和引理4可以得到,对任意球B,有 令 则 因此 接下来证明(8)式.对于k,i∈Z,k>i,可以得到 所以 先对I1进行估计.因为k>j,所以根据Tb的定义及尺寸条件(1)可得 故由引理6、引理4以及引理3可得 对于||fj||Lq(·)(ωq(·)),有 所以,当k>j时有 当1 当0 接下来对I2进行估计.由Tb的Lq(·)(ωq(·))有界性,可以得到 最后对I3进行估计,I3的估计与I1类似.因为k 当1 当0 综上所述,有 那么对于次线性算子的多线性交换子,根据上述原子分解理论,有 根据Tb的定义、尺寸条件(3)及广义的Hölder不等式可以得到 先对F1进行估计.因为k>j,所以由引理6可以得到 由引理1及引理4可得 当0 当1 最后,估计F2.类似地,当0 当1 所以 需要说明的是,定理2的结果在非齐次的情况下也是成立的.




1 预备知识和记号






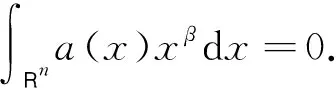
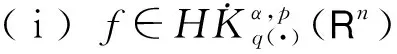




2 主要结果的证明



