触头系统结构对真空灭弧室温度场影响仿真

董华军, 温超阳, 刘林林, 郭方准

(大连交通大学 机械工程学院,辽宁 大连 116028)

0 引 言

随着真空灭弧室在小型化、大电流方向不断发展,由承载大额定电流而产生的温升过高的问题越来越受到重视[1-2]。温度过高对于真空灭弧室的机械强度及通流能力有着重要影响,因此,研究真空灭弧室的触头结构参数对其温度场分布的影响,对于真空灭弧室改善温升效应,优化其通流能力具有重要意义。

关于真空灭弧室温度场的研究方法,主要有解析法和数值分析法[3-10]。随着计算机仿真技术发展,温度场的数值算法得到推广,主要有有限元法和有限体积法[11],其中有限元法具有更高的稳定性和求解精度。通过磁热耦合的有限元法,人们对50 Hz真空灭弧室的温升分布进行了大量的研究。石磊团队建立了10 kV/5 kA真空断路器模型,模拟其温度场,研究散热器安放位置对温度分布的影响,但对于真空灭弧室发热过程中损耗分布没有分析;在此基础上,薄凯、叶逢春等引入多重边界条件,通过仿真不同电流条件下以及不同工况条件下触头温升过程,获得了触头温度与损耗分布。以上针对真空灭弧室的温度场研究,仅对灭弧室内部零部件等进行了简单的温升模拟,对于影响真空灭弧室温度分布的各项因素没有涉及,而在真空灭弧室工作过程中,诸如环境温度、风速等外部环境因素以及灭弧室自身结构参数等均对其温度分布有着较大影响。为探讨真空灭弧室温升影响条件,文献[5,9-10]等针对真空灭弧室安装工艺、散热系数、环境温度等外部因素对温升的影响,得到了真空断路器的温升情况与接触半径、接触位置和散热系数之间的变化关系。上述文献采用控制变量法对影响灭弧室温度场的外部环境因素进行了分析,对于真空灭弧室的散热设计有重要的参考意义。但针对真空灭弧室的各零件结构参数变化对于其温度场的影响,相关研究文献较少,结构变化会引起导电回路中电流密度分布变化,触头结构参数不合理,在通流过程中就会发生电流集中现象,造成触头温度过高,有巨大的安全隐患;再者在过去的研究中,为计算简便快捷大多采用磁热单向耦合法,忽略了仿真过程中电磁场与温度场之间的相互影响,但由于触头材料的温度特性,其物性参数会随着温度变化发生明显改变,若简单将其视为常数将会与实际情况产生误差[11]。因此在考虑材料物性参数的温度特性情况下,研究真空灭弧室各零件结构特别是触头结构参数变化对于真空灭弧室散热设计十分重要。

基于此,本文在考虑材料热物性参数的温度特性以及电流涡流效应的基础上,采用Ansys Maxwell与Transient Thermal软件,通过Feedback模块对真空灭弧室的温度场进行磁热双向耦合仿真分析。通过改变真空灭弧室结构参数,分析单一的结构变化对真空灭弧室的欧姆损耗以及各零部件最高温度的变化规律,为今后的触头结构设计和通流能力优化提供参考。

1 数学模型

1.1 涡流场仿真数学模型

(1)

涡流区内有

(2)

(3)

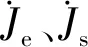
(4)

式中:Irms为所加载电流的有效值;S为导体横截面积。

该模型三维涡流场求解域边界条件如下:

1)在求解域边界面ΓH上施加无穷远边界条件,即

A|ΓH=0。

(5)

2)边界面ΓB为对称面,且磁感应强度法向分量为零,其边界条件为

Ay|ΓB=Az|ΓB=0。

(6)

采用有限元法计算得到真空灭弧室各部件平均损耗[14-15]为

(7)

式中:E为各部件单元总数;ΔVi为单元i的体积;ρe为单元电阻率;je和je*分别为单元电流密度的复共轭矢量。

1.2 温度场数学模型

对于真空灭弧室的热分析可假设如下[16]：

1)忽略真空灭弧室内部通过辐射散发的热量;

2)真空灭弧室材料各物理性能参数各向同性;

3)真空灭弧室表面的空气对流换热为无限空间自然对流换热;

4)环境温度不变。

根据傅里叶定律和能量守恒定律[17-18],可得真空灭弧室内部三维热传导微分方程

(8)

式中:ρ为材料密度;C为材料比热容;T为物体温度;t为时间;qv为单位体积内生成热。

真空灭弧室动、静触头导电杆外露部分及外壳外表面为对流换热边界条件,即

(9)

2 真空灭弧室有限元模型

首先利用Solidworks对真空灭弧室导电回路建模,模型相关参数如下:触头直径70 mm、杯厚8 mm、导杆直径45 mm、触头片厚4 mm、开槽长度30 mm、开槽角度25°。各零件图如图1所示,主要包括触头片、触头杯座、触头支撑盘、外壳。

图1 真空灭弧室三维模型

真空灭弧室在闭合时,动静触头表面的接触不是理想的面接触,而是离散的若干个点接触。为模拟真空灭弧室的动静触头接触情况,可用一圆柱体等效触头间接触斑点[19]。等效导电半径r为

(10)

式中:F为触头间预压力;ξ为触头表面接触系数,范围0.3～1,可反应接触表面的粗糙程度和弹塑性强度;H为材料布氏硬度。

初始模型建立好后,分别改变以下参数进行单因素仿真:触头直径改为55、60、65、70、75 mm;触头片厚改为3、4、5 mm;触头片开槽长度改为15、20、25、30 mm;杯厚改为4、6、8、10 mm;导杆直径改为30、35、40、45、50、55 mm。

3 仿真与分析

将灭弧室的几何模型保存成特定格式,并导入Ansys workbench中的Maxwell 3D模块进行涡流场仿真,材料设置如表1所示[20],其中电导率为20 ℃下数值。不同温度电导率计算公式如下:

表1 材料属性

(11)

添加激励为1 250 A,频率50 Hz,考虑灭弧室金属导体的涡流损耗,求解后得到真空灭弧室导电回路的欧姆损耗,将其导入温度场模块,计算系统的温度场,通过Feedback模块实现热场与涡流场的数据联动,实现双向耦合。环境温度采取软件默认的22 ℃,对流换热系数10 W/(m2·k),各材料不同温度下的热导率、比热容数值可由文献[21]查得。

3.1 初始模型对比仿真结果分析

从图2中看出2种耦合方式均在触头接触处颜色最深,说明电流密度值在接触处最大,电流密度沿触头片径向递减,且双向耦合电流密度略高于单向。由于实际中,接触电阻是以收缩电阻以及膜电阻的形式存在,而真空环境中,膜电阻可忽略,所以电流会集中于触头面的微小凸起,而电流密度图中,电流密度最大就位于接触电阻位置,说明接触电阻建模正确。在图3中,欧姆损耗的分布对应电流密度分布,其最大值仍然位于触头接触处,沿触头径向递减,仍然是双向耦合略高于单向,可见考虑材料热物性参数温度特性对于电流密度及损耗大小有着重要影响。因此,可预测真空灭弧室导电回路的温度最高值也位于触头接触处,且双向耦合模型温度高于单项耦合。

图2 电流密度云图

图3 欧姆损耗分布云图

图4为2种耦合方式温度场云图,左侧为单向耦合结果,右侧为双向耦合结果。温度分布以触头片为原点,随着轴向长度增加温度逐渐下降,在动静导杆部分,温度呈对称分布,这是由于在触头接触处电流产生收缩现象,形成收缩电阻,导致温度升高。最高温度位于触头接触处,数值为双向86.829 ℃,单向76.023 ℃。各零件的温度场如图4所示:触头片的温度由中心向边缘逐渐递减,由于开槽存在偏角,将触头片分割成6个部分,每部分槽端之间距离比触头边缘槽尾之间距离要窄,因此电流在槽端处有一定程度集中,所以此处的温度会比边缘稍高,这也是云图中产生“梅花”形状的原因;触头杯座杯指顶端温度最高,沿杯指旋向逐渐降低;支撑盘与触头片接触一侧温度最高,沿轴向递减,这与整体温度云图中一致;外壳温度两边高中间低,这是因为外壳两端与金属端盖接触,由于真空环境下,热量主要通过导体热传导传递,热辐射可忽略不计,所以外壳温度是由两端向中间递减。图5为2种耦合方式下,真空灭弧室各零部件温度随时间变化情况。由图可知当时间达到6 000 s以后,温升不在明显,温度趋于稳定,且触头片的温度变化曲线与真空灭弧室整体温度变化曲线几乎重合。

通过比较2种耦合方式发现双向耦合无论是整体温度还是单个零件温度均高于单项耦合,由材料电导率公式也可知,当温度升高时,电导率会随之降低,意味着材料电阻会增大,因此双向耦合温度会高于单项耦合,此外,本仿真结果最高温度为86.829 ℃,文献[22]在电流为1 250 A下实验结果为80.3 ℃,本文与之相比误差为7.9%,误差较小,仿真结果可用于真空灭弧室温度场分析中。下文将分析双向耦合下温升分布随结构变化情况。

为方便分析结构对温度的影响,将每种结构的变化引起的损耗变化以及温度变化用曲线图表示。

3.2 改变导杆直径的仿真结果分析

图6所示为改变导杆直径后,灭弧室的欧姆损耗及温度变化曲线。由图看出,当导杆直径由30 mm增大到55 mm过程中,真空灭弧室的欧姆损耗随导杆直径的增大而减小,当导杆直径为50 mm时损耗下降不再明显;图6(b)为温度时变曲线,可得当时间道道6 000 s后各导杆直径下,真空灭弧室最高温度区域稳定,增长不再明显,且对应损耗图六条时变曲线之间间距越来越小。由于导电杆直径的大小直接影响其电阻的大小,直径越大,其截面积就越大,因此电阻就越小,最终导致导电回路温升降低。但导杆直径不能无限增大,这会加重操动机构的负载,因此在设计导杆时,在满足使用要求的前提下,因尽可能减小导杆直径。

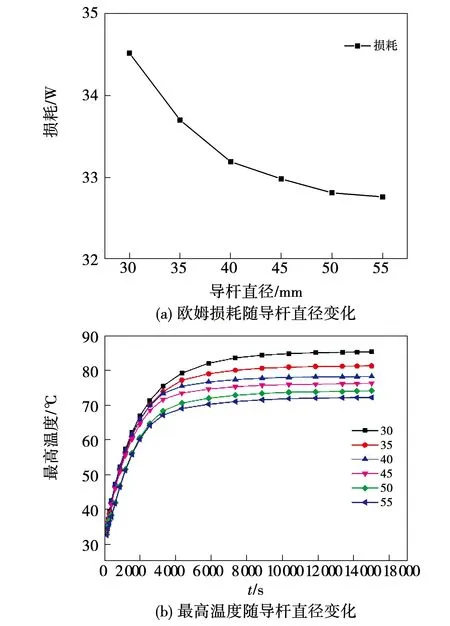
图6 相关量与导杆直径的关系曲线

3.3 改变触头直径的仿真结果分析

图7为改变触头直径后损耗、温度变化曲线。可以看出,当触头直径由55 mm增大到75 mm过程中,损耗迅速下降,但当触头直径超过60 mm时,损耗下降趋势不在明显;温度时变曲线对应损耗曲线,触头直径由55 mm到60 mm时迅速下降,之后下降趋势变缓,各触头直径下温度均在6 000 s后趋于稳定。因此继续增大触头直径对温升的降低意义不大,还会增大操动机构的负载。之所以会有这样的趋势是因为在杯厚不变的情况下,当触头直径增大时,触头片与触头杯座的接触面积会增大,两部分的接触电阻就会减小,所以温升开始下降非常明显,但在整个回路电阻中,主要是触头片之间的接触电阻决定温升大小,在触头预压力不变的前提下,接触半径不会改变,因此整体的回路电阻变化不大,这也是当触头直径增大到60 mm以后温升下降趋势不在明显的原因。

图7 相关量与触头直径的关系曲线

3.4 改变触头杯厚的仿真结果分析

图8是改变触头杯厚时,损耗和温度变化曲线。随着杯厚的增加,真空灭弧室损耗先迅速下降后下降减缓,而温度时变曲线也随杯座厚度的增加逐渐下降,当杯厚增大到8 mm后,继续增大杯厚对于降低温升的效果不在明显。增大触头杯厚降低温升的原理与增大触头直径相同,都是增加了触头片与触头杯座的接触面积,降低了接触电阻,但由于主要电阻仍位触头片之间的接触电阻,且杯厚持续增大不利于灭弧室的小型化,还会增大操动机构的负载,因此杯厚为8 mm时效果最佳。

图8 相关量与杯座厚度的关系曲线

3.5 改变开槽长度的仿真结果分析

图9为触头片开槽长度对欧姆损耗和温度的影响变化曲线。分析可知,随着开槽长度的变大,触头片之间接触面积会减小,接触电阻变大,导体电阻的增大致使电流流过时产生的欧姆损耗增多,最终导致温度增大。在触头片开槽有利于减小触头片上产生的涡流,进而减小由涡流产生的剩余磁场,有利于真空灭弧室的开断,但在存在一定偏角开槽的触头片上,一味的增加槽长,会导致两槽之间距离减小,使电流经过此处时路径增长,电流密度增大,温升就会变大。因此有文献指出槽长因控制在触头直径2/3以内,所以,在设计过程中,开槽长度不能过大。从最高温度变化的范围看,相较于导杆直径、触头直径与杯厚,开槽长度对最高温度的影响较小。

图9 相关量与开槽长度的关系曲线

3.6 改变触头片厚的仿真结果分析

表2、图10分别是改变触头片厚度引起的损耗和温度变化。分析可知,当增大触头片厚度时,导体产生的欧姆损耗会随之降低,灭弧室最高温度也会降低,如图11所示,这是由于触头片厚度的增加导致流经触头片中心的电流密度降低,且触头片越厚,其内部电流密度分布越均匀,有利于降低由电流集中带来的温升效应,但由于厚度变化范围有限,导致灭弧室最高温度变化不大。在设计触头片厚度时,要考虑触头开断时磁场滞后时间,根据相关文献,厚度越大,磁场滞后时间越长,因此在满足温升要求的前提下,应使厚度尽可能小。

表2 损耗随触头片厚度变化

图10 最高温度随触头片厚度变化

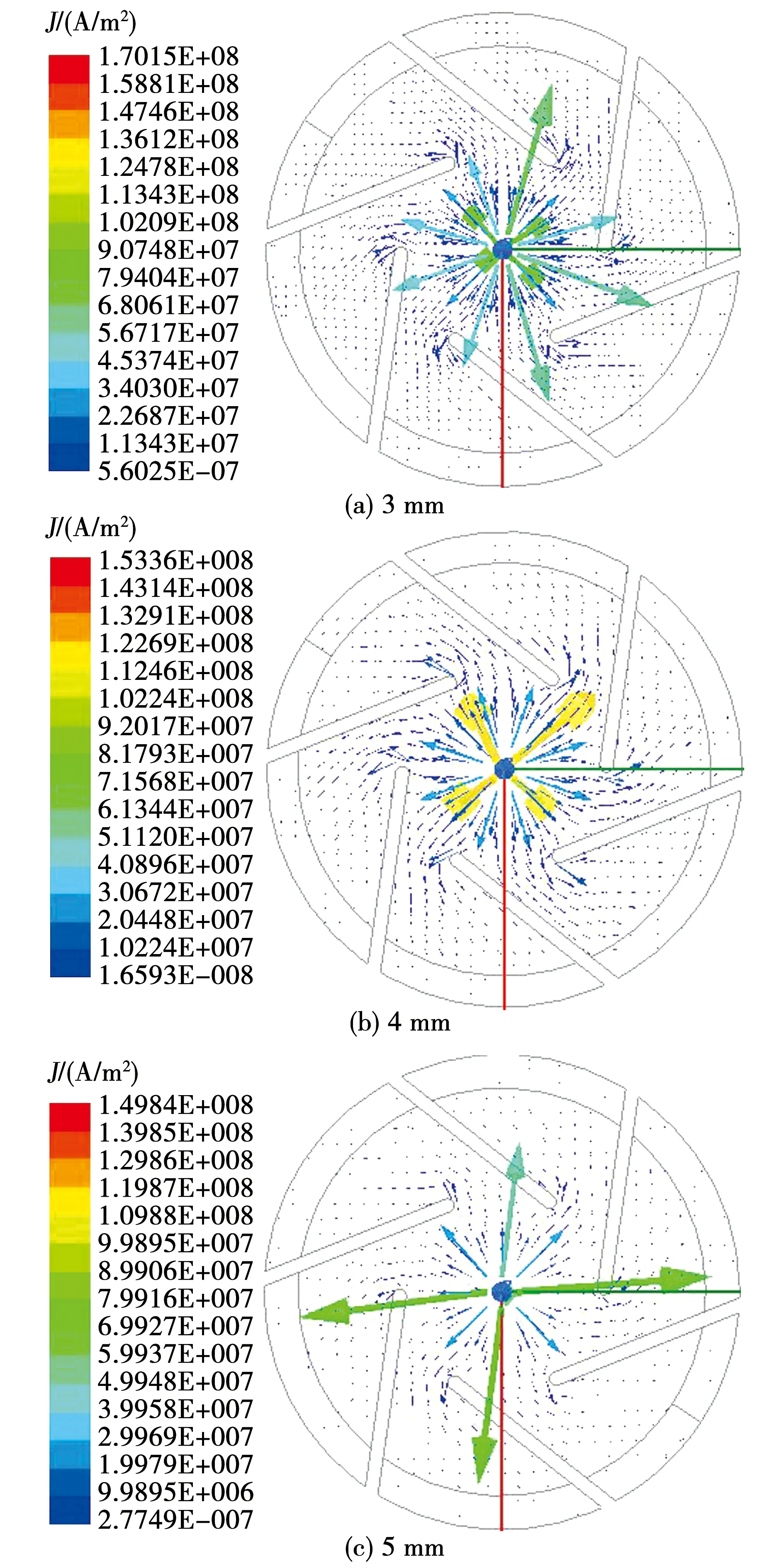
图11 改变触头片厚度时电流密度分布云图

4 讨 论

通过对上述仿真结果数据进行整理,触头系统结构对真空灭弧室温度场的影响结果如表3所示。

表3 结构对温度场的影响结果

从表3看导杆直径、触头直径、触头杯厚与触头片厚对真空灭弧室的温度场均有影响,而开槽长度对其影响较小。根据上文针对结构参数变化对于灭弧室温度场影响分析,可得出真空灭弧室最佳结构参数:导杆直径55 mm、触头直径65 mm、触头杯厚8 mm、开槽长度20 mm、触头片厚度5 mm。将此参数下的模型进行温度场仿真如图12所示,真空灭弧室最高温度为70.952 ℃,与优化前相比温度降低18.3%,由此可得改变触头系统及导杆的结构参数对于降低真空灭弧室温度是有效的。

图12 优化后真空灭弧室温度场

5 结 论

本文通过磁热双向耦合仿真方法,考虑材料温度特性的情况下,研究了真空灭弧室触头的5种结构参数变化对其温度场的影响,得出以下结论:

1)真空灭弧室的最高温度位于动、静触头的接触位置,且通过灭弧室各部分零件将热量通过热传导向外传递,经磁—热双向联动,灭弧室最高温度在6 000 s后趋于稳定;

2)真空灭弧室导电回路产生的欧姆损耗与灭弧室最高温度随着导杆直径、触头直径、触头杯厚、触头片厚增加而降低,随开槽长度增加而上量上升,且导杆直径、触头直径、触头杯厚对温度的影响较大,而开槽长度与触头片厚对温度影响较小;

3)经过本文分析,在本文参数范围内,真空灭弧室最佳结构参数为:导杆直径55 mm、触头直径65 mm、触头杯厚8 mm、开槽长度20 mm、触头片厚度5 mm,此模型最高温度较优化前降低18.3%。