不同绕组绕法对高频变压器分布电容及波形的影响
2023-09-19叶志军胡杰林晓明曾文辉罗继亮
叶志军, 胡杰, 林晓明, 曾文辉, 罗继亮
(1.华侨大学 信息科学与工程学院,福建 厦门 361021; 2.福州天宇电气股份有限公司,福建 福州 350012; 3.国网泉州供电公司,福建 泉州 362000)
0 引 言
21世纪以来,随着绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)、金属-氧化物半导体场效应晶体管(metal-oxide-semiconductor field-effect transistor,MOSFET)等电力电子开关器件的发展和非晶、纳米晶合金材料的普及,高频化已成为磁性元件的主要发展动态[1-2]。提升工作频率能保证设备在正常运行的前提下,尽可能地减小铁磁元件的质量和体积,提高整体设备的功率密度[3]。高频变压器作为电子电路中重要的磁性元件,在整个电路中起着原边和副边的电气隔离、调节电压的作用。与传统变压器相比,高频变压器在性能效率、制造成本、运输安装等方面都具有更明显的优势,其应用场合从最早的通讯设备和计算机电源扩展到如今的大容量直流-直流变换器和电动汽车等新兴领域,因此高频变压器未来具有广阔的发展前景[4]。
由于工作在高频工况下,分布电容对高频变压器的影响不可忽视,如在开关电源中,分布电容对电路系统的影响是复杂多变的,但集中表现在影响绕组的高频阻抗特性[6]、增加整机功耗[7]、损坏开关元器件[8]、电磁干扰(electromagnetic interference,EMI)[9]4个方面。
近年来关于高频变压器分布电容的研究比较广泛且深入,文献[10]提出了三电容、四电容和六电容等效模型,并以电路分析的方法推导了几类等效模型的转换方法,最后通过双绕组变压器验证了转化的可行性。文献[11]指出减小变压器层间电容和层间电压有利于提高运行可靠性,并且设计了Z型绕法和三角形绕法的变压器,大幅改善了电压分布。文献[12]通过MATLAB软件仿真分析,总结并得出了输出波形与分布电容之间的关系,并在此基础上验证了优化绕组结构是一种减小分布电容的有效方法。文献[13]以反激式开关电源为例,研究绕组不同的绕法和排列布局对分布电容大小的影响,得出改变变压器分布电容值可以有效抑制开断时的电流尖峰。文献[14]根据特定频率下漏感和分布电容将会产生谐振电流,并以电流的变化特点提出一种新的测量分布电容的方法。文献[15]将绝缘层的厚度作为分布电容的主要影响因素,通过Maxwell仿真得到了不同层间距下的分布电容值,并绘制了分布电容值与层间距的变化曲线,确定了最优绝缘厚度,且绕制的实物样机测试效率为99.4%。
综上所述,现有的参考文献大都关注于电容等效模型、不同的绕法和排列布局对分布电容的影响等方面的研究,而忽略了高频变压器分布电容最终对电源尖峰电流的影响。
本文根据静电场理论分析高频变压器绕组中的电位分布情况,推导分布电容的计算公式,并通过3种不同绕法的高频变压器实验验证理论的正确性,提出分布电容的大小是影响开关电源原边电流尖峰的重要因素。
1 分布电容的计算方法
计算分布电容通常是通过计算绕组间的电场能量W,再以电容储能公式等效出来,即
(1)
式中:ε为绕组间的介电常数;E表示绕组间的电场强度的大小;V代表绕组的体积大小;u表示相邻的绕组层间的电压;U1为输入电压等级;d为绕组间的间隙长度。由公式可以看出,高频变压器分布电容的大小与层间的电压分布有关,而层间的电压分布又与变压器的绕组绕法密切相关,所以当采用不同绕法时,变压器的分布电容也不相同。目前变压器的绕组绕法主要有C型绕法、Z型绕法和分段式绕法3种。
1.1 C型绕组分布电容计算
对于C型绕法的绕组情况,其绕法示意图如图1(a)所示,电位分布如图1(b)所示,每两层间的电位分布如图1(c)所示。
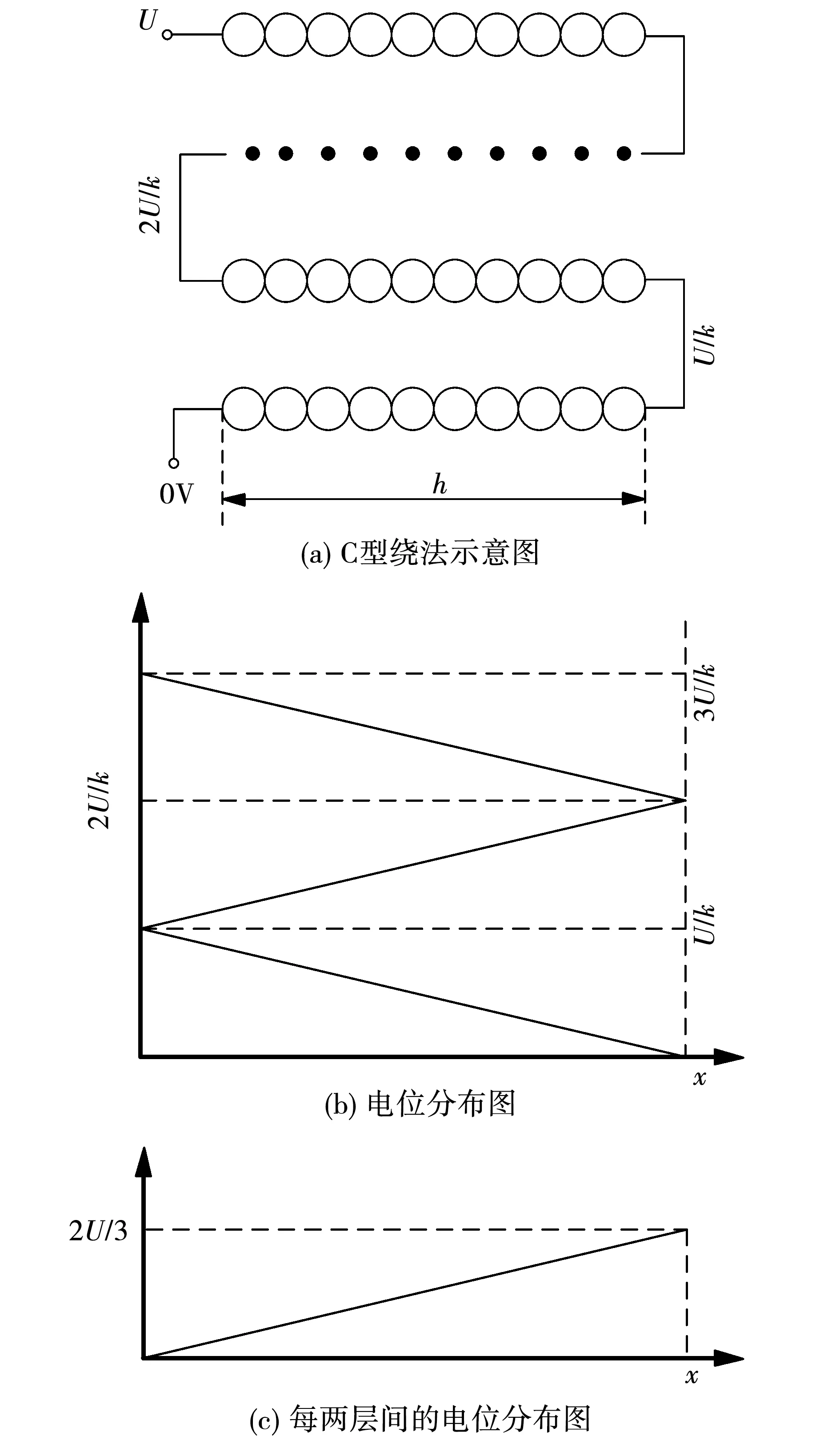
图1 C型绕法绕组模型及电位分布图
设绕组层数为p,层间距离为Δk,由图1(c)可知每两层间随高度h的电压差分布都是从0 V线性上升到2/pU,所以层间任意高度x的电场强度为
(2)
代入电场能量公式求得两层间绕组存储的电场能量为
(3)
则每层间的分布电容大小为
(4)
原边线圈总的分布电容为
(5)
1.2 Z型绕法分布电容计算
当采用Z型绕法时,其绕法示意图如图2(a)所示,电位分布如图2(b)所示,每两层间的电位分布如图2(c)所示。

图2 Z型绕法绕组模型及电位分布图
在绕组的各个绝缘间隙中电压随线圈的高度成线性变化,且每一层的变化率相同,如图2(c)所示,各层间的电压差ΔU=U1/p,则每层间的电场强度为
(6)
一层间存储的能量为
(7)
由电场能量公式等于分布电容能量得两匝线圈之间的电容为
(8)
则原边线圈总的分布电容为
(9)
1.3 分段式绕法分布电容计算
采用分段式绕法时,其绕法示意图如图3(a)所示,电位分布如图3(b)所示,每一段中两层间的电位分布如图3(c)所示。
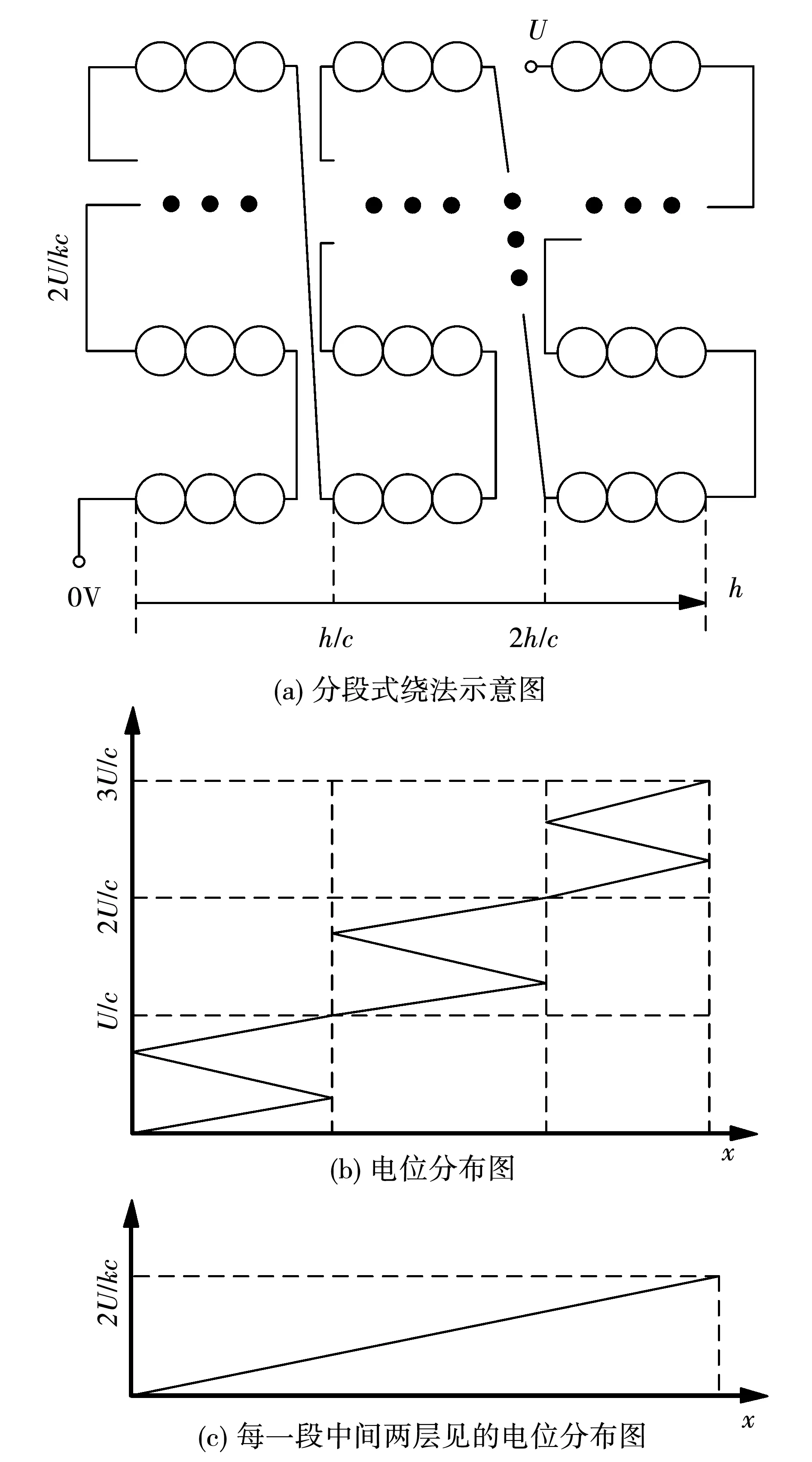
图3 分段式绕法模型及电位分布图
图3(a)中,分段式绕法的绕组类似于多个C型绕法的绕组相串联,设c为分段数,则每一段C型绕法绕组的电压为U/c,图3(b)所示为分段数和层数为3时的绕组电位分布图。在每一段分段式绕法的两层中,其电势差为
(10)
代入电场能量公式求得两层间绕组存储的电场能量为
(11)
则每层间的分布电容大小为
(12)
原边线圈总的分布电容为
(13)
2 实验模型及计算方法的验证
2.1 高频变压器实验模型
本文设计并绕制了3台不同绕法的高频变压器,分别为C型、Z型和分段式绕法。磁芯采用EPC46型铁氧体磁芯,导线采用直径为2 mm的圆导线,一次侧8匝,二次侧68匝,绕组高度为18 mm,绕组等效长度为60 mm,绕组间的绝缘距离为0.8 mm。绕制的变压器实物如图4所示。

图4 3种不同绕法的高频变压器实物图
2.2 有限元仿真模型与分布电容计算
通过Ansys Maxwell进行模型仿真,在软件中采用静电场求解器对高频变压器的分布电容模型进行分析,设置各材料属性,在设置激励时按照模拟电压在绕组上线性增加的条件将绕组分为若干个小块,在小块上按照一定梯度设置激励模拟电压线性增加的条件。如图5所示为不同绕法电场强度分布云图。

图5 不同绕法电场强度分布云图
对于C型绕法,从图中可以看出,其电场强度分布是不均匀的,分布规律为从上端到下端电场强度由零逐渐上升到最大值;而Z型绕法的绕组间电场强度处处相等;对于分段式绕法,图中将绕组分为两段,每一段都是一个C型绕法,因为其电位梯度的距离减小,所以其层间电场强度较小,但由于分段数较小,在分段处形成了较大的匝间电场能量,如图5(c)中绕组中间部分。通过Maxwell自带的场计算器可计算所选区域中的电场能量,通过下式可求出绕组中分布电容的大小,求出的分布电容大小如表1所示:

表1 不同绕法分布电容仿真大小
(14)
2.3 测量系统的搭建及分布电容测量
高频变压器分布电容不是一个实际的电容器结构,而是一个等效电容,将绕组中分布的电场能量集总到一个电容中存储的能量,此电容在等效电路中就表示为分布电容。其测量方法常采用谐振法测量,基本原理为高频变压器二次侧空载,其等效电路如图6所示。
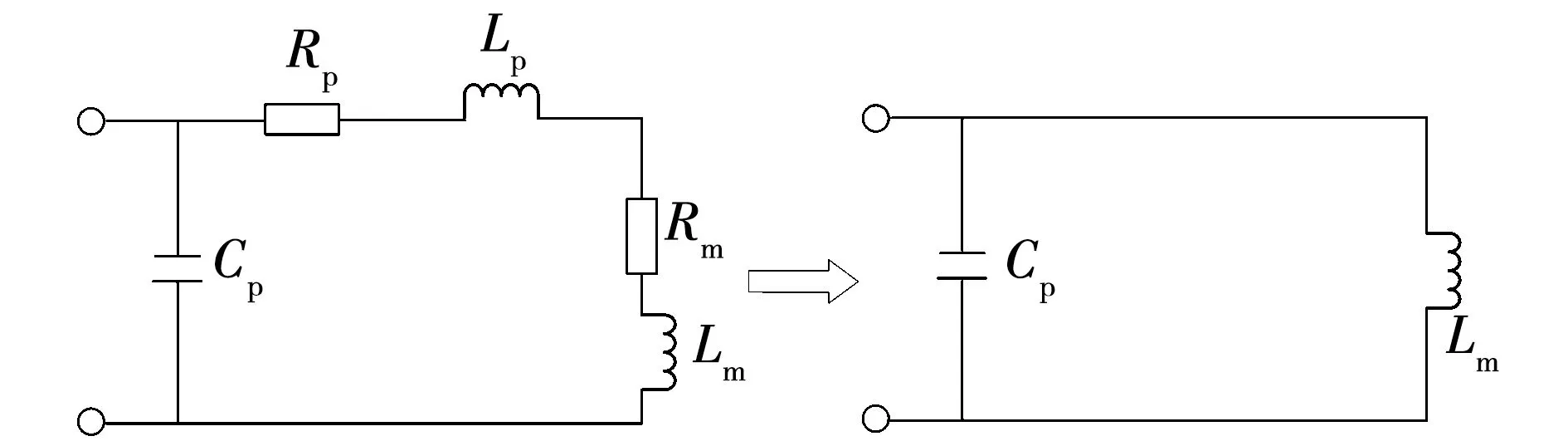
图6 高频变压器分布电容测试原理
图6中:Rp为一次侧绕组等效电阻;Lp为一次侧漏感;Rm为励磁电阻;Lm为励磁电感。由于磁芯的导磁系数比空气的导磁系数要大的多,所以Xm≫Xp,Rm≫Rp,故Zm≫Zp。又由于高频变压器绕组发生谐振时工作在较高的频率,Xm=ωL≫Rm,所以高频变压器在二次侧空载时可以等效为励磁电感和分布电容并联,在一次侧接入阻抗分析仪,进行频率扫描,当高频变压器励磁电感和分布电容发生谐振时,阻抗角为零度,可得到谐振关系式为
(15)
从谐振关系式可以解得分布电容计算式为
(16)
实际测量时采用BODE100阻抗分析仪对3种不同绕法的高频变压器进行测量,其测量结果见图7~图12。
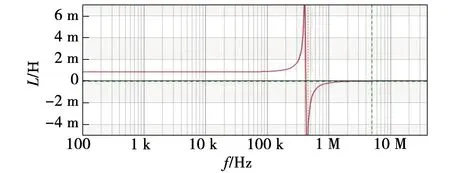
图8 C型绕法电感随频率变化图

图9 Z型绕法阻抗角随频率变化图

图10 Z型绕法电感随频率变化图
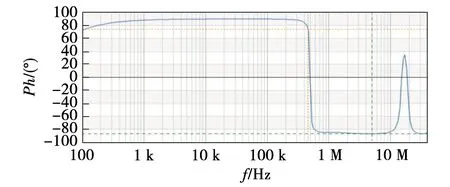
图11 分段式绕法阻抗角随频率变化图

图12 分段式绕法电感随频率变化图
在实验中分别将3个高频变压器样机在100 Hz~10 MHz的宽频范围内测量了其电感和分布电容参数,如表2所示。
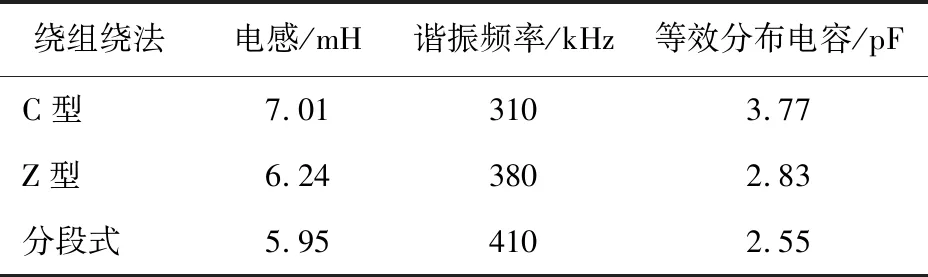
表2 高频变压器绕组参数测量结果
2.4 结果比较与分析
结合理论分析、有限元仿真法和高频变压器实物样机测试,其分布电容模型计算、仿真、测量比对如表3、表4所示。

表3 高频变压器分布电容模型验证

表4 分布电容误差分析表
表4中误差1的计算公式为
(17)
误差2的计算公式为
(18)
式中:Ccal为分布电容理论计算值;Cexp为分布电容测量值;CFEM为分布电容仿真值。分析表4可知,C型绕法、Z型绕法及分段式绕法的理论计算值、仿真值以及测量值之间的误差均在10%以内,验证了上述提出的计算分布电容方法的正确性,从而得出了C形绕法最大,Z形绕法次之,分段式绕法最小的结论。
3 分布电容对高频变压器工作电路的影响
为了探究分布电容对高频变压器工作电路的影响,本文将所绕制的3种不同绕法的高频变压器接入其工作电路中,本文所选用的电路为推挽电路,其原理图如图13所示。

图13 推挽电路原理图
当u1为高电平,u2为低电平时,Q1饱和导通,Q2截止,输入电压通过Q1加在变压器原边N2和N3上,在变压器线圈上产生感应电动势,副边二极管D1和D4导通流过电流。当u2电压高于u1,Q2饱和导通,Q1截止,此时N1和N4上的电压为输入电压,负半周期的工作原理和正半周期相同。
当开关管导通瞬间,不仅是开关管的电压瞬时跃变,绕组两端的电压也快速跃变,由零上升为电源电压,在高频变压器的工作状态中需要考虑分布电容,因此较大的尖峰电流将会在高频变压器原边产生,如图14所示。

图14 原边电流波形图
使用Ansoft Maxwell与Simpleror联合仿真的方式对推挽变换器进行仿真。通过比较3种不同绕制方法的高频变压器在电路中的产生的原边电流尖峰大小来判断分布电容对开关电源的影响。首先在Ansoft Maxwell软件下通过建模得到C型绕法、Z型绕法、分段式绕法的高频变压器模型,通过调用Ansoft Maxwell软件与Simpleror软件的连接,在Simpleror软件中建立仿真的逆变及整流部分,如图15所示。

图15 推挽电路仿真图
其仿真得结果如图16~图19。
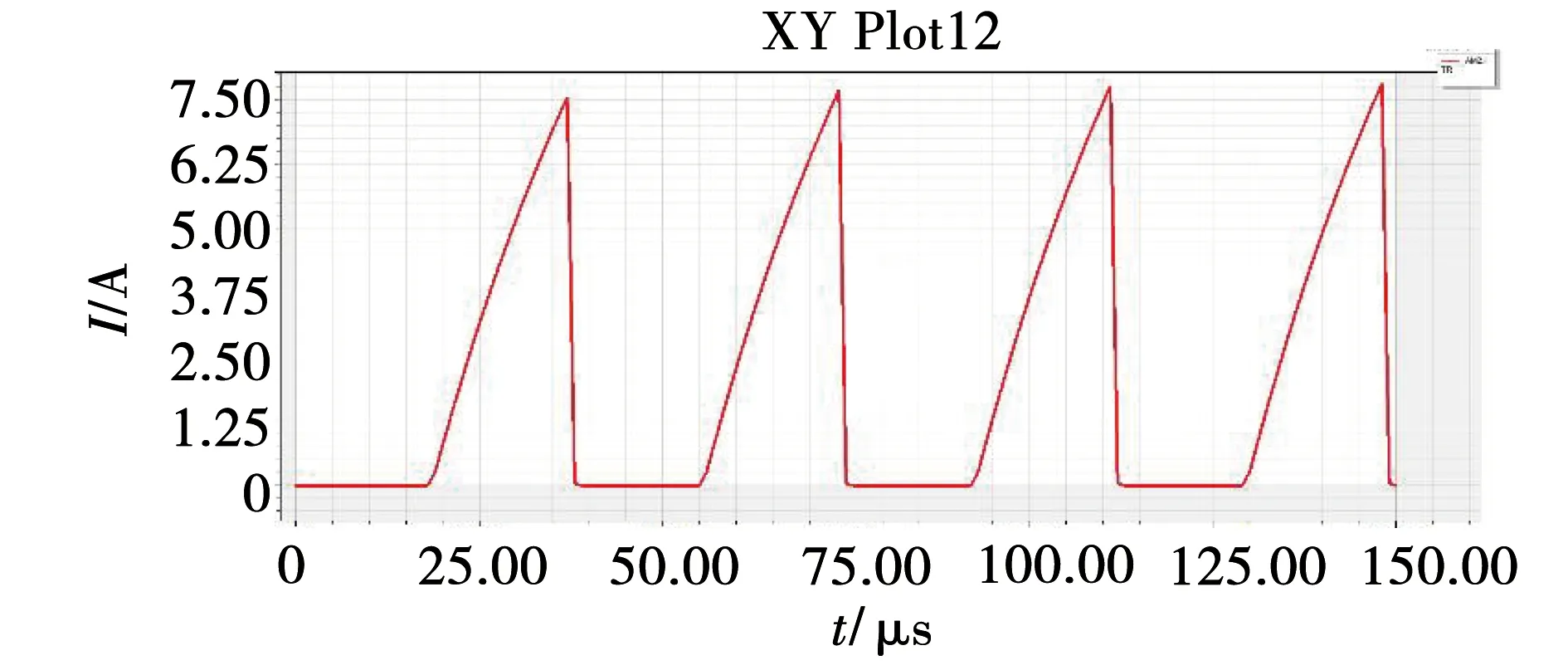
图16 不考虑分布电容原边电流仿真图

图17 C型绕法原边电流仿真图

图18 Z型绕法原边电流仿真图
从图17中可以看出,C型绕法的原边电流尖峰为3.8 A,Z型绕法的原边电流尖峰为3.2 A,分段式绕法的原边电流尖峰为2.8 A,C型绕法的最大,分段式绕法的最小,而理想的高频变压器不存在电流尖峰。
在实际测量中,将3种不同绕法的高频变压器带入推挽电路中,通过一台示波器测量原边电流的波形,测量结果如图20~图22所示。

图20 C型绕法原边电流波形测量图
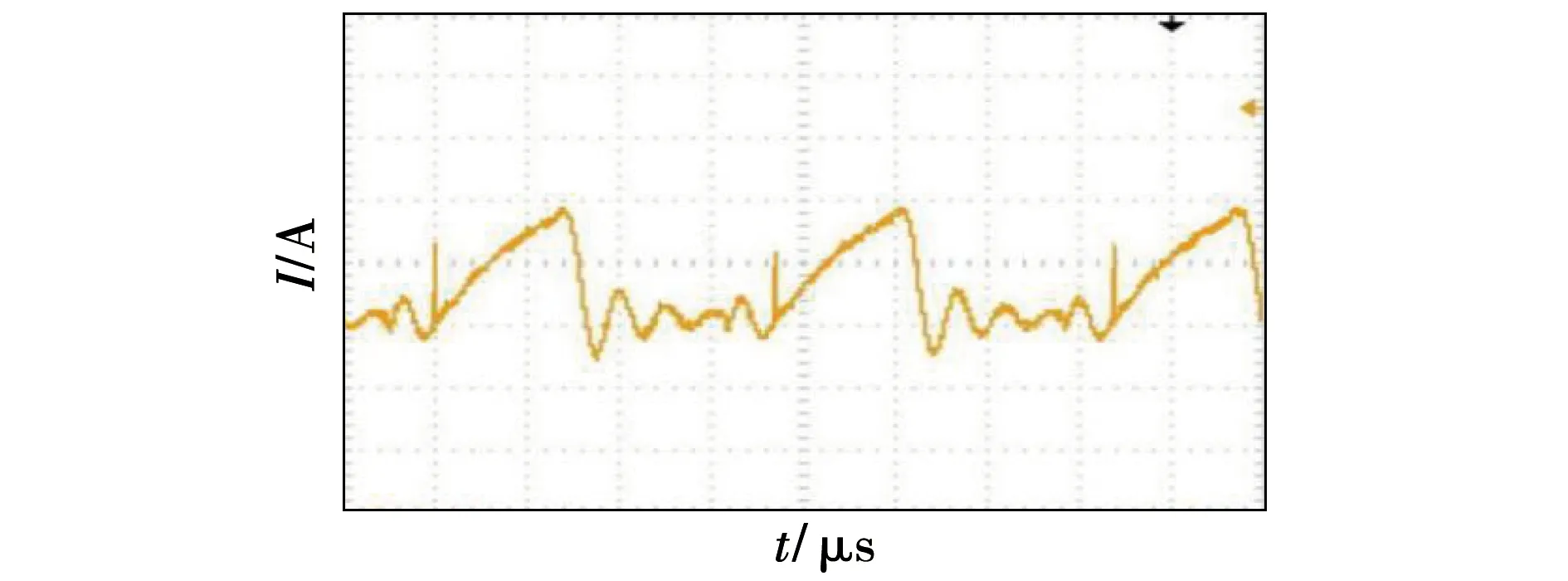
图21 Z型绕法原边电流波形测量图

图22 分段式绕法原边电流波形测量图
从实际测量的结果可以看出,C型绕法的高频变压器原边产生的电流尖峰为3.4 A,Z型绕法为2.8 A,分段式绕法为1.9 A。从上述结果分析可以得出,若高频变压器的分布电容越大,则原边尖峰电流的值也越大,对其工作电路的影响也越不利。采用C型绕法分布电容最大,分段式绕法最小。而通过改变高频变压器的绕法,可以减小分布电容的大小,从而削减原边电流尖峰。
4 结 论
本文基于静电场理论推导了高频变压器分布电容的计算方法,并考虑了绕组绕法对分布电容大小的影响,在此基础上,针对3种不同绕法的绕组,通过有限元的方法建立了相应仿真模型,并实际绕制了3种不同绕法的高频变压器实物模型,通过一台阻抗分析仪实际测量了分布电容大小。对比计算、仿真和测量的结果,验证了高频变压器分布电容的正确性。
还将3种不同绕法的高频变压器带入推挽式开关电源中,分析分布电容对电路运行的影响。使用Ansys Maxwell与Simplorer软件进行联合仿真,并将C型绕法、Z型绕法及分段式绕法变压器接入到推挽式开关电源中,再对变压器一次侧绕组电流进行测量。测量结果表明,分布电容越大,原边引起的电流尖峰越大,而通过改变绕组绕法的方式,能有效减小分布电容,从而削减原边的尖峰电流。
