遗传算法对三线圈无线电能传输系统参数优化

杨云虎, 梁大壮, 洪若飞, 徐寒

(安徽工业大学 安徽省高校电力电子与运动控制重点实验室,安徽 马鞍山 243000)

0 引 言

无线电能传输(wireless power transmission,WPT)也被称为感应电能传输,它通过电磁场耦合来进行能量传输[1-3]。由于消除了电源和负载之间的物理接触,WPT系统可以大大提高电气设备的灵活性和安全性。

两线圈WPT系统相关理论目前比较完善,广泛应用于手机等电子产品、生物医学植入物等[4-5]短距离无线充电的场合。虽然两线圈WPT系统结构简单,但在传输距离较长的情况下,存在能量传输效率低、抗偏移性能差等问题。三线圈WPT系统是在两线圈中间加一个中继线圈,它不仅能大大增加了能量的传输距离,而且能提升抗偏移性能,因此相对两线圈WPT系统,三线圈WPT系统具有传输距离远、传输效率高和抗偏移性强等优点。目前,三线圈WPT系统得到了较多的研究与应用,如单发射双接收的三线圈WPT系统可用于同时为多个小功率移动装置无线供电[6],双发射单接收的三线圈WPT系统[7]以及带有中继线圈的单发射单接收三线圈WPT系统[8]也已应用至电动汽车等无线充电领域,不仅能提升能量传输距离,而且能提升系统的抗偏移性能。

文献[9]介绍了一种两线圈的无线电能传输系统,并使用遗传算法优化了多个参数,但并未考虑到输出功率。文献[10]通过改进的遗传算法来优化微机器人胶囊无线电能传输系统的谐振频率、线圈匝数、线圈半径等参数,使系统的输出功率达到86.6 mW,传输效率达到8.01%,虽然将效率与输出功率的乘积作为目标函数进行优化,但并没有将线圈之间的距离作为优化变量。文献[11]仅仅针对提高传输效率的问题,将传输效率、传输距离、电压增益等指标作为目标函数,使用多目标优化算法来优化系统参数。文献[12]提出了一种基于遗传算法的数值优化方法,通过考虑频率、线圈内半径、线圈长度、线圈电感、线圈电阻和匝数等设计约束,给出了保证最高线圈品质因数的最佳线圈参数,但并没有考虑到提高品质因数给系统输出功率和效率带来的影响。

由于以上文献研究的不足,本文以三线圈的线圈匝数、线圈边长、线圈距离和频率等9个变量作为优化变量,使用遗传算法计算出系统效率与输出功率的乘积的最大值,以此来求取效率的最大化与输出功率最大化的折中值,实现系统性能的最优。

1 三线圈系统模型分析

1.1 电路模型分析

图1为三线圈无线电能传输系统原理图,U为逆变器输出电压有效值,R1、R2和RL分别为发射电路寄生电阻、中继电路寄生电阻和接收线圈负载,C1、C2和C3分别为发射线圈补偿电容、中继线圈补偿电容和接收线圈补偿电容,I1、I2和I3分别为发射线圈电流、中继线圈电流和接收线圈电流的有效值。

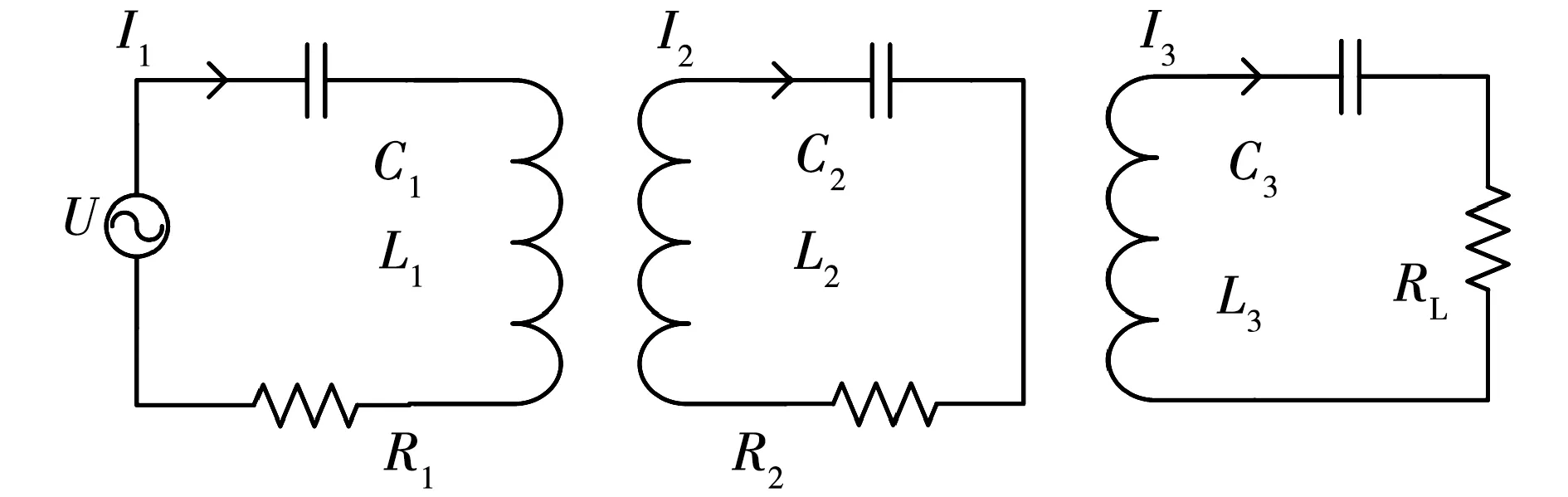
图1 三线圈无线电能传输系统原理图

由基尔霍夫定律可知

(1)

其中:M12为发射线圈与中继线圈之间的互感;M23为中继线圈与接收线圈之间的互感;M13为发射线圈与接收线圈之间的互感。

可将Z1、Z2和Z3表示如下:

(2)

各线圈消耗的功率可表示为:

(3)

则系统效率可表示为

(4)

即

η=

(5)

对以上建立的三线圈输出功率模型与效率模型进行Matlab三维可视化,得到三线圈系统输出功率与互感M12和互感M23变化的关系,如图2(a)所示,三线圈系统传输效率与互感M12和互感M23变化关系,如图2(b)所示。

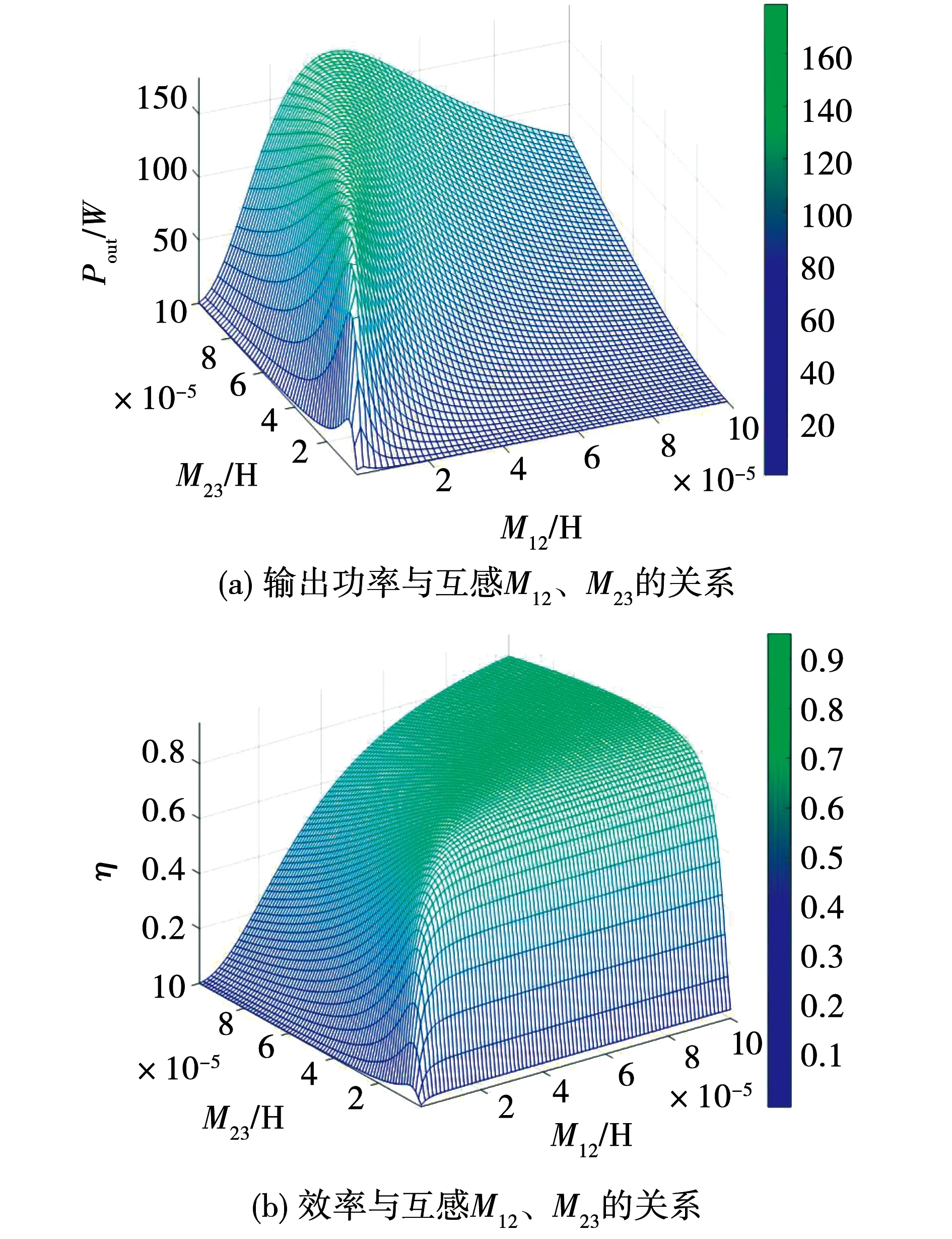
图2 效率与输出功率三维曲面图

从图2(a)中可以看出,系统的输出功率随互感M23的增大而增大,系统的输出功率随M12的增大时先增大,后减小。从图2(b)中可以看出,系统效率随M23的增大是先增大后减小,系统效率随M12的增大而增大。从两图中可看出,在同一互感范围内,系统的效率与输出功率不能同时达到最大值。因此,本文将优化的目标函数定为效率与输出功率的乘积,取效率最大值与输出功率最大值的折中值。

1.2 效率与输出功率模型分析

系统效率与输出功率可表示如下

ηPout=

(6)

改变三线圈的线圈匝数、边长和距离的实质就是改变线圈互感,忽略发射线圈与接收线圈之间的互感,则同轴方形平面线圈互感的计算公式可表示如下:

(7)

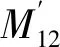
2×(2v-z-z′)]

(8)

其中:a1和a2为线圈边长;μ0为真空磁导率,μ0=4π×10-7H/m。t、t′、v、z和z′物理意义如图3所示。

图3 同轴矩形回路互感

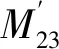
线圈电阻R的计算公式可表示为

(9)

其中:ρ为铜的电导率,室温条件下ρ=1.75×10-7;S为导线的横截面积;a为线圈边长;r′为线圈导线半径;l为线圈总长;N为线圈匝数。为减少集肤效应和邻近效应,也为了避免因缆线太粗而降低互感计算的精度,所有线圈均采用Φ0.1×130Litz线绕制。

由以上公式可以得到一个以线圈匝数N1、N2和N3、线圈中心匝边长a1、a2和a3、频率f、发射线圈与中继线圈之间的距离D12、中继线圈与接收线圈之间的距离D23为参数的效率与输出功率优化模型如下:

ηPout=ψ(N1,N2,N3,a1,a2,a3,f,D12,D23)。

(10)

因此,三线圈无线电能传输系统的优化目标如下

Min(-ψ(N1,N2,N3,a1,a2,a3,f,D12,D23))。

(11)

2 非线性约束条件分析

为避免算法陷入局部最优解,也为了避免在实际应用中能量的太多浪费,因此限制其最低效率为80%,限制条件如下:

η≥80%。

(12)

图4为利用Ansoft Maxwell辅助分析发射线圈的有限元模型。

图4 发射线圈有限元模型

从图4(a)、图4(b)可以看出在发射线圈内部,距离发射线圈边缘越远,磁场分布就越少,且线圈边缘附近的磁场最强,线圈中心点磁场为零,因此,为避免因3个线圈尺寸差异过大造成磁通损失,加入以下线圈匝数和线圈边长的非线性约束条件:

(13)

为简化系统模型,必须使互感M13忽略不计,因此加入以下非线性约束条件:

(14)

除了以上的约束条件之外,对N1、N2、N3、a1、a2、a3、f、D12、D23也有以下相应的边界约束:

(15)

由以上可得整个系统的数学优化模型如下:

(16)

3 遗传算法的编码实现

因为9个变量所组成的目标函数极为复杂且非线性约束条件的存在使目标函数变得不连续,所以传统的需要目标函数的导数值等其他一些辅助信息才能确定搜索方向的算法(如最小二乘估计算法与BP神经网络算法)不适用于此类优化。

遗传算法仅使用由目标函数值变换得来的适应度函数值,无需目标函数的导数值等其他一些辅助信息,因此使用遗传算法来解决此类问题就显得比较方便。另外,遗传算法的选择、交叉、变异等运算都是以一种概率的方式进行,其搜索过程的灵活性是其他算法无法比拟的。遗传算法的操作流程图程如图5所示。

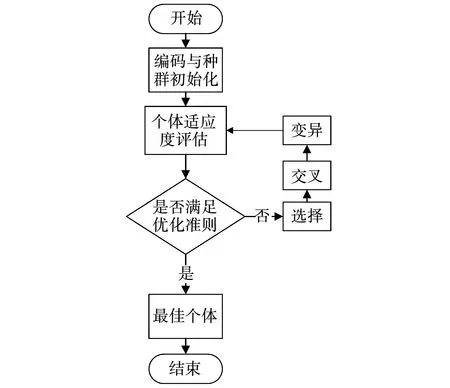
图5 遗传算法工作流程图

3.1 编码与种群的初始化

编码是遗传算法需要解决的问题,迄今为止人们已经提出了许多编码方法,浮点编码方法适用于在遗传算法中表示范围较大的数字,也适用于较大空间的遗传搜索,并且也便于处理复杂的决策变量约束条件,因此本文对优化变量采取浮点编码的方法,则优化参数的染色体为

X=[x1,x2,x3,x4,x5,x6,x7,x8,x9]=

(N1,N2,N3,a1,a2,a3,f,D12,D23)。

(17)

一般情况下,初始种群越大,算法搜索时间就越长,算法不容易遍历整个空间,容易出现局部最优解,初始种群选取过少的话容易使算法出现早熟,种群单一。一般来讲,初始种群选择为20～100。但考虑到优化变量较多,将种群数量选取为500,迭代次数为55。

3.2 个体的适应度评估

个体适应度评估就是根据个体适应度大小来评估各个个体的优劣程度,从而决定其遗传到下一代概率的大小,本文中,适应度函数设置为

fi=-ψ(N1,N2,N3,a1,a2,a3,f,D12,D23)。

(18)

3.3 遗传算子

3.3.1 选择

选择运算使用比例选择算子,比例选择算子是利用比例于各个个体适应度的概率决定其子孙遗传可能的一种选择方法。若种群数为M,个体i的适应度为fi,则个体i被选取的概率Pi为

(19)

个体选择概率给定后,产生0～1之间的均匀随机数来决定哪个个体参与交配,个体被选择的概率高,则可能被多次选中,其基因会在种群中不断扩大。个体被选择概率小,则被选择的次数也少,其基因在种群中不断减少,以此来达到优胜劣汰的目的。

3.3.2 交叉

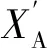
(20)

其中α为换算系数,其取值在-0.25～1.25之间,此算法能将搜索范围扩大。

3.3.3 变异

(21)

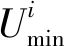
因为有9个待优化的变量,所以不可避免的会产生多个近似最优解,尽管实现最优解的变量组合不只一种,但ηPout的值基本相同,表1中列出了算法计算出的最优解与次优解。

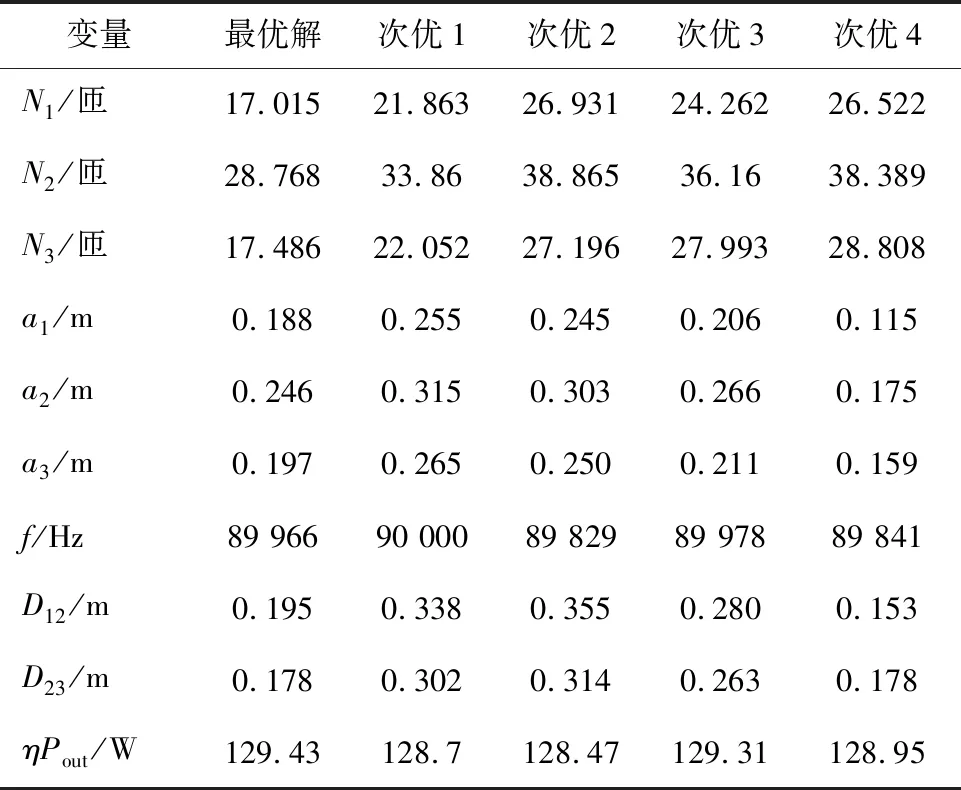
表1 最优解与次优解

虽然这几种次优解的ηPout基本相同,但是这几种次优解的线圈匝数、线圈中心匝边长均大于最优解的匝数与边长,为节省有色金属资源,采用了使用有色金属较少的最优解。另外,这几种次优解的传输距离都过长,不满足实际应用。

下图6为最优解遗传优化迭代曲线。

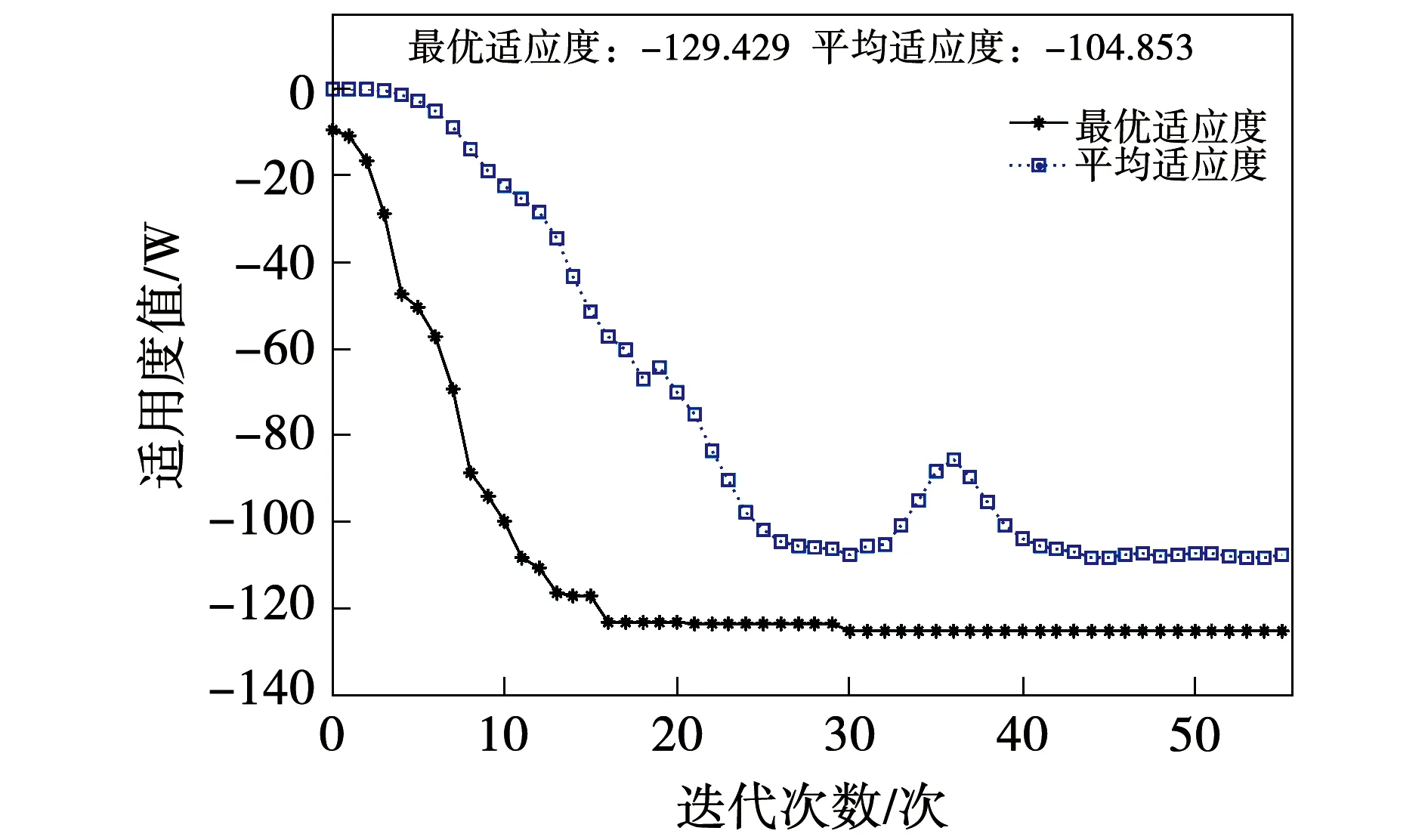
图6 遗传优化迭代曲线

4 仿真与实验验证

根据遗传算法计算出的最优解,可得电路中的参数,如表2所示。

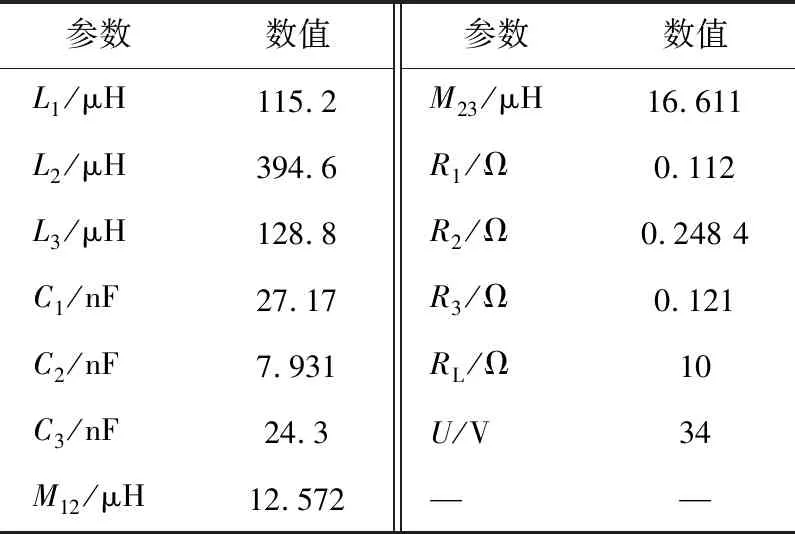
表2 三线圈无线电能传输系统参数

通过Simulink仿真可得出ηPout=123.23 W,其中η=0.810 2,Pout=152.10 W,与遗传算法计算出的结果相符合。

图7(a)为三线圈WPT实验平台,图7(b)为最优解时逆变器输出电压波形与线圈电流波形,电压与电流有效值以及频率均在图7(b)中标注。

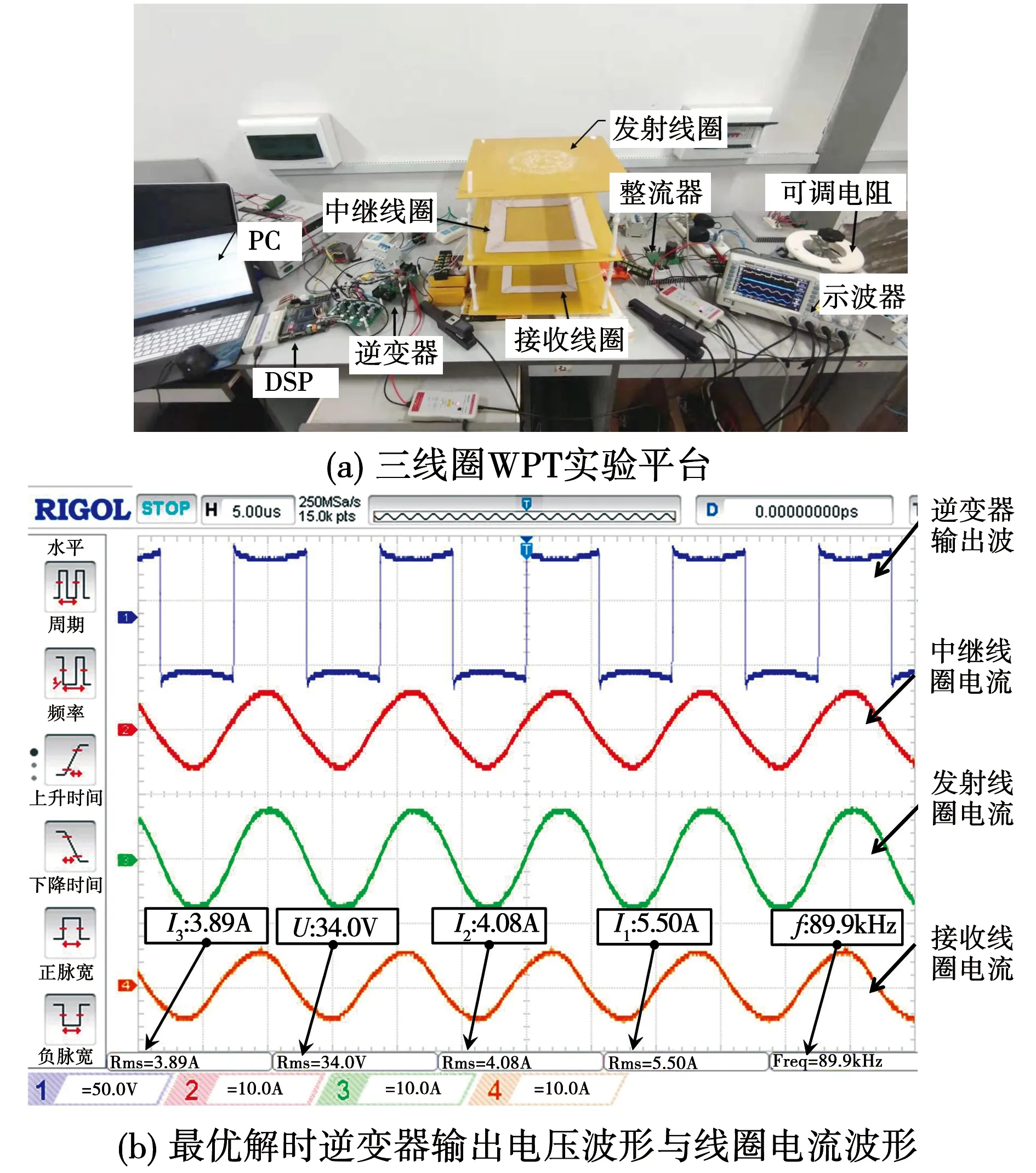
图7 实验平台和波形图

图8为通过仿真和实验来验证算法优化的正确性,图8(a)、图8(b)、图8(c)、图8(d)分别为其他变量为最优值的条件下,通过减小D12、增大D23、增大D13以及减小D12的同时,保持D13不变来验证最优匝数合理性所得的折线图。

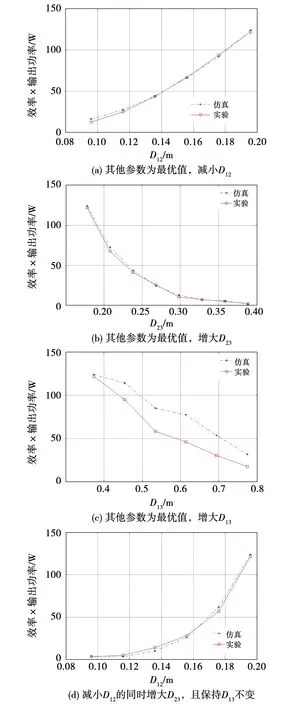
图8 线圈距离最优解的实验与仿真验证

图8(a)中,D12的最优值为0.195 m,若继续增加D12来验证,会使互感超出公式(14)的这个非线性约束条件,即超出了合理的搜索范围,超出了这个合理范围的验证是没有意义的。图8(d)中,如果通过增大D12,减小D23,且D13不变来验证距离的最优性,则系统效率会迅速降低,超出公式(12)这个约束条件,即效率低于80%,超出这个效率的非线性约束条件,系统的实用性会降低,没有验证的意义。图8(b)、图8(c)在一定范围内验证其最优性也是为了避免其范围超出第二节所设置的非线性约束条件。

由图8(a)中可以看出,当固定接收线圈与中继线圈之间的距离以及其他变量为最优值,且逐渐减小发射线圈与中继线圈之间的距离D12时,仿真和实验的结果表明效率与输出功率的乘积在逐渐下降。图8(b)为固定发射线圈与中继线圈之间的距离以及其他条件为最优值,逐渐增加中继线圈与接收线圈之间的距离D23所得到的折线图,从图中可以看出,仿真和实验所得的效率与输出功率的乘积都在逐渐下降。图8(c)为保持中继线圈位置和其他变量不变时,同时等距离增加D12与D23的距离所得到的折线图。当逐渐减小发射线圈与接收线圈之间的距离时,能看出效率与输出功率的乘积随着距离D13的增加而逐渐下降,图8(d)亦如此。以上四幅仿真与实验所得的数据对比图验证了线圈之间的距离为最优解。

美国汽车工程师协会(SAE)将轻型电动汽车无线充电的标准频带范围确定在85 kHz,频带范围为81.38～90 kHz。为满足这一标准,本文中频率参数f选择范围为85～90 kHz,图9(a)为逐渐减小频率f来验证f的最优性,从图9(a)中可以看出,在这一标准频带内,算法所计算出的f是最优的。由于单独增大或减小中心匝边长a2都会超出公式(13)中的非线性约束条件|a1-a2|≤0.06或者非线性约束条件|a2-a3|≤0.06,即超出合理的寻优范围,因此,验证a2的最优性是没有意义的。从图9(c)图中可以看出,当逐渐减小发射线圈的匝数N1时,效率与输出功率的乘积逐渐下降,如果增大最优匝N1来验证,则验证范围超出公式(13)中的非线性约束条件|N1-N2|≤12,单独增大和减小N2、N3都会超出非线性约束条件|N1-N2|≤12或者|N2-N3|≤12,即超出合理的优化范围,因此,没有验证的意义,同理图9(b)、图9(d)中若有超出合理优化范围的验证也是没有意义的。从图9(b)、图9(c)、图9(d)这两个图中可以看出,遗传算法所得的中心匝边长与匝数是最优的。

图9 工作频率、线圈匝数和线圈中心匝边长最优解的实验与仿真验证

5 结 论

本文建立了以线圈匝数、线圈边长、频率和线圈距离等参数为优化变量的优化模型,并考虑到磁矢线最大化利用等因素而加入了非线性约束条件。为了实现系统的整体最优,将效率与输出功率的乘积作为优化目标,然后通过遗传算法对系统模型进行计算,将计算出的最优参数通过仿真和实验进行验证,仿真和实验结果表明,遗传算法计算出的结果是最优的,满足实际应用要求。

本文采用的遗传算法不仅对三线圈无线电能传输系统能进行有效分析,且研究方法简单,研究结果精准,而且可推广到类似的多参数、多约束条件且数学模型复杂的系统中去。