永磁直线电机端部力抑制措施

韩雪岩, 刘景铭, 朱龙飞

(沈阳工业大学 国家稀土永磁电机工程技术研究中心,辽宁 沈阳 110870)

0 引 言

随着近几年《中国制造2025》计划顺利实施,我国高端数控机床和机器人领域也在高速发展,而与此相关的直线电机及直接驱动方式也将大面积替代传统旋转电机+滚珠丝杆驱动方式,因此克服了传统伺服系统中由机械转换机构带来的效率低、体积大、精确度低等缺陷,趋向于高精确度与高可靠性方向发展。永磁直线同步电机(permanent magnet linear synchronous motor,PMLSM)由于其定位精确度高,响应速度快,高刚度与可靠性的同时,维护简单且噪声低,被广泛应用到高精确度数控机床,光刻机等工业自动化领域中[1-4]。

然而,随着PMLSM直接驱动方式实现机床进给系统零传动,PMLSM自身推力波动也会直接作用于伺服控制系统,影响电机控制精确度与运行平稳性。所以削弱PMLSM推力波动将会极大提高电机应用范围与控制精确度。

目前PMLSM推力波动来源可分为端部力、齿槽力、电磁脉动力、摩擦力、负载扰动等,其中摩擦力和负载扰动属于外部干扰[5],在推力波动中占比较小,而电磁脉动力是由于电枢绕组合成磁动势和空载反电势存在谐波波形,导致电磁推力包含谐波成分不能平稳输出的力[6],常规解决手段为在控制器中施加电流滤波器[7]。根据上述分析,推力波动主要由端部力和齿槽力产生,端部力和齿槽力也合称为磁阻力。相比之下,端部力对电机推力波动的影响程度较大,所以针对端部力的削弱对降低推力波动具有重要意义。

针对如何削弱端部力,国内外学者提出了多种优化措施。文献[8]中对端部力用傅里叶级数推导出直线电机最优长度公式,但计算仅停留在理论层面,并未验证计算公式的可行性。文献[9]中利用解析计算,从削弱谐波角度优化电机动子长度,可有效降低端部力,但计算基础模型过于理想,无法对通用电机求解。文献[10]提出磁块结构,改变磁块参数可有效削弱端部力,并进行实验验证。但考虑到磁块结构相关参数较多,并未进行多参数优化,只是进行局部求解,不能保证端部力最大程度削弱。文献[11]中通过对PMLSM端齿处开倒角,可有效的削弱端部力,并用有限元仿真进行验证,但文献中对边齿开倒角并未从理论角度分析原因,只是单纯的利用有限元分析进行优化。

本文首先通过实验平台验证仿真计算磁阻力结果的准确性,然后设计一台11极12槽永磁直线同步电机,并从初级结构和端齿结构两方面削弱端部力。针对初级结构,通过解析计算和有限元仿真,计算出最优初级长度;针对端齿结构,分别采用底部倒角结构,端部磁块结构,梯形磁块结构3种方法削弱端部力。其中针对梯形磁块结构,采用Kriging 模型与多目标遗传算法相结合对结构优化设计。最后对比优化措施,选出最优结构,满足电机性能指标。

1 空载推力波动计算实验验证

本文采用已有11极12槽直线电机样机进行实验,验证空载推力波动仿真结果的准确性。直线电机样机结构参数如表1所示,直线电机样机图如图1所示,直线电机实验原理图如图2所示。

图1 直线电机样机图

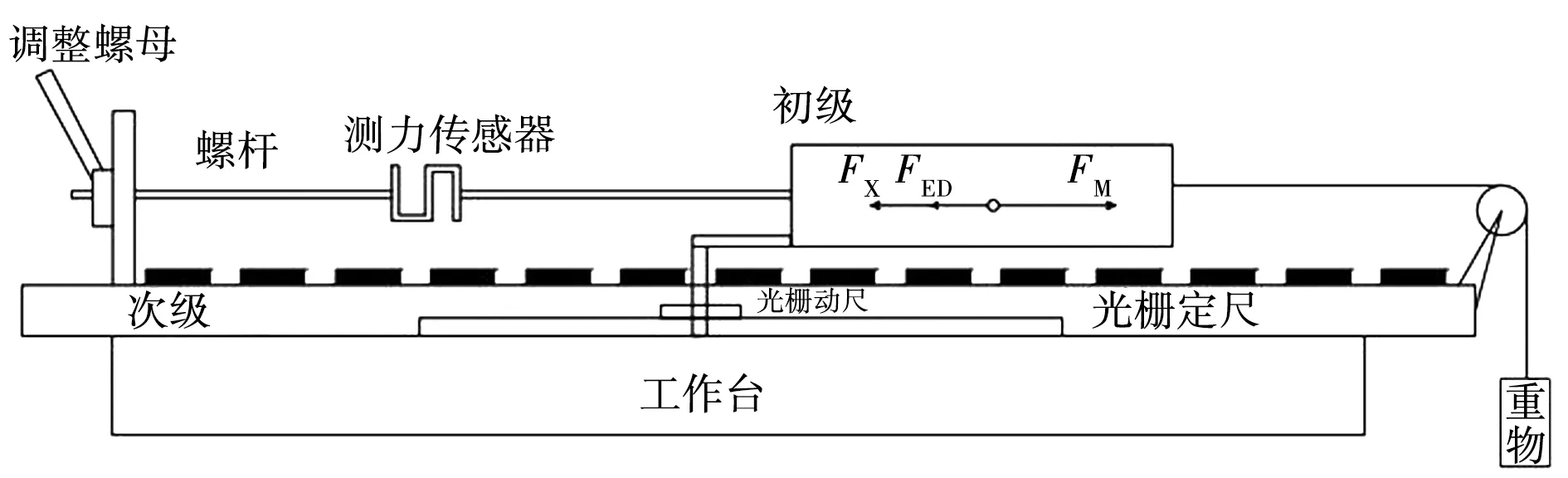
图2 直线电机实验原理图

表1 样机结构参数

实验中空载推力波动的计算原理如下:

空载测量时的计算公式为

FED=FM-FX。

其中:FM为重物负载产生的力;FED为空载推力波动;FX为由测力计测出的拉力。实验中空载推力波动通过重物负载力与测力计拉力相减得到。

对于重物重量产生的拉力可以认为是由测力计产生的拉力和空载推力波动与之平衡。首先对电机模型进行实验测试。实验测试空载推力波动结果与仿真结果如图3、图4所示。实验值与计算值的比较如表2所示。

图3 实验测试空载推力波动波形

图4 有限元仿真空载推力波动波形

表2 直线电机空载推力波动的实验值与计算值

实验测得曲线与有限元仿真曲线存在一定误差,这是由于实验受到测试平台的限制,只能0.5 mm测试一点数据。而考虑到直线电机在推力波动一个周期内位移16 mm,一个周期只能取32个点。对于11极12槽电机,齿距15 mm,每经过15 mm齿槽力波形经过11个周期,用32个点测量得到的结果不精确,所以实验结果相比于有限元仿真结果存在误差,二者曲线只能大致吻合。而推力波动峰峰值误差在2.7%左右,仿真结果与实验数据相差不大,初步验证仿真计算结果的准确性。

2 直线电机初始模型设计

本文参考实验样机,设计一台11极12槽永磁直线电机,电机仿真模型如图5所示。电机性能指标参考雅科贝思公司AKM系列直线电机,直线电机性能指标如表3所示,电机主要尺寸参数如表4所示。

图5 电机仿真模型

表3 直线电机性能指标

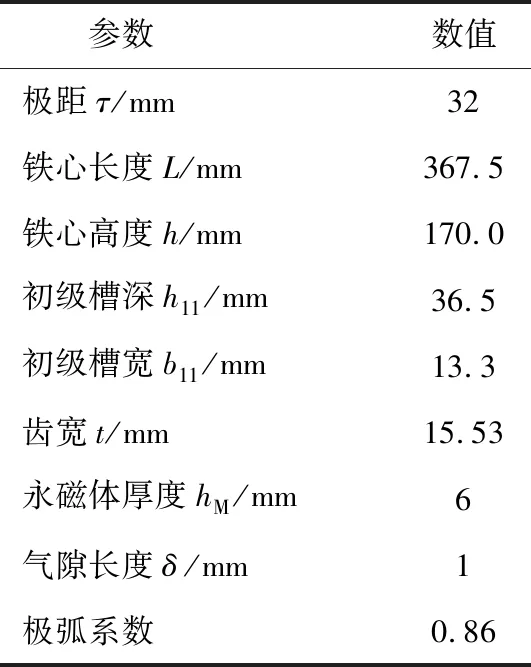
表4 电机主要尺寸参数

对电机的推力与推力波动进行有限元仿真,如图6所示。

图6 电机推力波形

直线电机平均推力2 012.3 N,推力波动峰峰值283 N,由于电机推力波动百分比14.4%≥5%,不满足电机推力波动性能指标,所以后文从初级长度和端齿结构两方面抑制端部力,降低电机推力波动。

3 电机初级长度优化

由于本文直线电机动子长度大于2倍极距,所以端部力可等效2个半无穷长度电枢端部受力的合力。如图7所示,左右端部力波形近似周期为一个极距的正弦波,通过改变动子长度来调节左右端部力互差相位,即可削弱端部力。

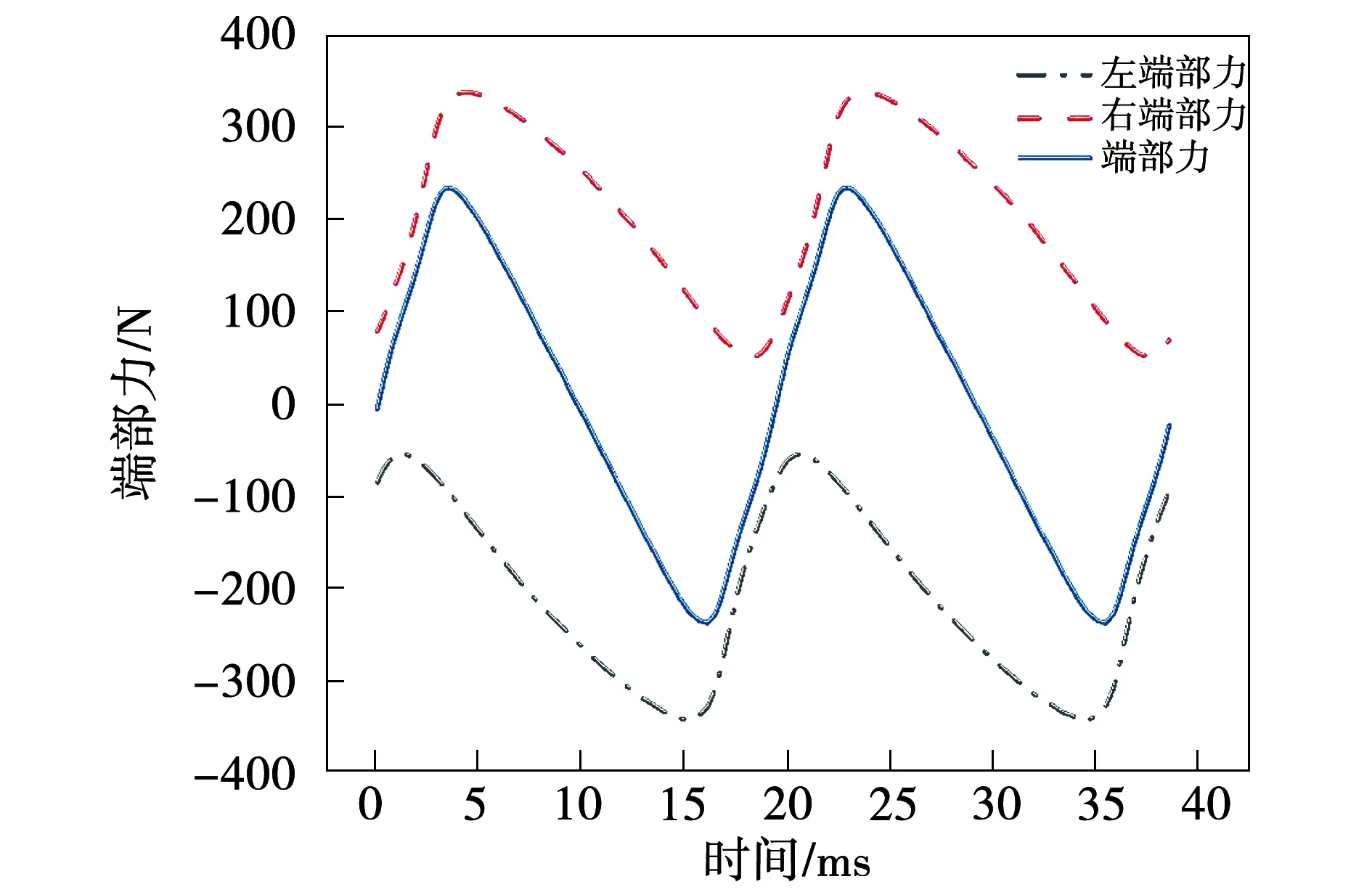
图7 端部力波形

将左右端部力波形用傅里叶表达式表示,对其合力进行解析计算。左右两端端部力表达式以及合力表达式分别为:

(1)

(2)

(3)

式中:σ=L-mτ,L为初级长度;m为任意正整数;FR、FL分别为左右端部力;F为端部力合力。

对式(3)进一步整理可得

(4)

考虑到单一结果对直线电机最优长度选择的不准确性,所以对式(4)可以分成两种情况考虑,确定最优长度范围。

第一种情况,满足下式:

(5)

(6)

第二种情况,当x=L时,满足下式:

(7)

(8)

式中:n取值为1;k为任意正整数(这里取值为1)。

根据式(6)、式(8),分别计算出2个长度值为368 mm和374 mm,即合适初级长度在368～374 mm范围内。并在此范围利用有限元分析计算电机推力波动峰峰值和平均推力,确定电机最优初级长度。电机368～374 mm推力波动峰峰值和平均推力如表5所示,变化趋势如图8所示。

图8 不同初级长度推力和推力波动峰峰值变化图

表5 电机不同初级长度平均推力和推力波动峰峰值

由表中数据可知,直线电机初级长度为371 mm时,电机的推力波动峰峰值最小为195.7 N,相比于初始模型,电机推力波动削弱了30.8%,验证了解析计算结果的可靠性,利用解析式计算出直线电机可选初级长度范围,避免大量利用有限元仿真,节省时间。

相比于初始长度367.5 mm,初级长度371 mm时,电机推力增加满足性能指标要求,推力波动虽然不满足性能指标但也有大幅度削弱,所以后文在此电机初级长度基础上对电机推力波动进行优化。

4 电机端齿结构优化

根据文献[12],利用能量法对端部力进行解析计算,即

(9)

得其幅值为

(10)

式中:δ为等效气隙长度;μ0为真空磁导率;k1为磁通压缩系数;τ为极距;lef为动子铁心叠压长度;φm为端部纵向磁通最大值。

由式(10)可知,电机的端部纵向磁通最大值对端部力影响程度最大,所以本文通过优化边齿结构抑制纵向磁通,降低端部力。本文分别采用电机边齿倒角结构,端部磁块结构和一种新型的梯形磁块结构3种边齿结构对比计算。

4.1 边齿倒角结构

由于电机边齿底部磁密较大,所以本文对边齿底部削角,抑制纵向磁通,降低端部力。倒角设计方案如图9所示,削角前后电机边齿处磁力线变化如图10所示。

图9 倒角设计方案

图10 削角后端部磁力线分布图

由图10可知,底部削角对直线电机端齿底部磁力线有明显改善。验证了底部倒角削弱端部力的可行性。本文对倒角长度x和倒角高度y参数化计算。图11为不同倒角长度与高度时永磁直线同步电机的推力与推力波动变化图。

由图11(a)可见,随着倒角长度x和倒角高度y增加,电机的推力逐渐减小,在x<14 mm且y<2.4 mm时,电机推力大于2 000 N,满足性能指标。所以在此区域内,选取推力波动最小值点。

由图11(b)可见,当倒角横向长度x=12 mm,纵向长度y为2 mm时,电机推力波动为最小值,降低到117.3 N,且推力为2 004.2 N,推力满足指标要求,相比于电机最优初级长度时,推力波动削弱58.5%。

4.2 端部磁块结构

端部磁块结构的想法来源于电器学中分磁环的理论,其结构如图12所示,在磁极端面一部分套上一个导体块作为分磁环,分磁环存在可以使通过正常支路磁通与经过有分磁环支路磁通之间出现了相位差[13]。

图12 分磁环结构图

而本文参考电器学中分磁环结构放置方法,在电机端齿外侧合适位置贴加一种与铁心材料相同的端部磁块结构,电机端部磁块结构见图13。

图13 电机端部磁块结构

由于电机端齿底部纵向磁通密度较大,所以应用端部磁块结构调节电机纵向磁通分布。通过调整磁块位置,抑制纵向磁通,进而削弱端部力。但考虑到电机总长需要满足最优初级长度,添加磁块会导致电机总长变长,所以将一部分电机初级长度等效成端部磁块,这样既能保证电机最优长度不变还能利用磁块结构削弱推力波动。电机磁块等效图见图14。

图14 端部磁块等效图

考虑到纵向磁通的削弱的同时,负载推力也有所削弱,为了满足电机性能指标,需要选择合适的位置来放置端部磁块。所以本文主要针对磁块长度a,磁块高度b,磁块上移高度h,3个结构参数进行参数化计算。

由于对3个结构参数进行参数化分析,计算量较大,所以先利用控制变量法,计算单个变量对直线电机推力与推力波动的影响情况。然后对主要结构参数进行参数化计算。单个变量对推力与推力波动的影响情况见图15。

图15 单个变量对推力与推力波动的影响情况

由图15可见,磁块高度b对电机的推力与推力波动影响最小,这是因为边齿纵向磁通集中在边齿底部,磁块变高对纵向磁通影响不显著。基于图中变化情况,本文确定电机磁块高度为14 mm,然后利用有限元分析磁块长度a和磁块上移高度h对推力和推力波动的影响情况,结果见图16。

图16 不同磁块长度和磁块上移高度电机的推力和推力波动

图16(a)显示,推力随着磁块长度a增加和磁块上移高度h增加而降低。当磁块长度a≤8 mm,磁块上移高度h≤1.6 mm时,推力大于2 000 N,满足指标要求,所以在此区域内,选取推力波动最小值点。

图16(b)显示,在推力满足性能指标范围内,当磁块长度a=8 mm,h=1.4 mm时,电机推力波动最小值为90.7 N。

所以初步选取磁块长度a为8 mm,磁块高度b为14 mm,磁块上移高度h为1.2 mm,电机推力波动为90.7 N,推力为2 003.2 N,相比于电机初始模型,推力波动削弱67.9%。

4.3 梯形磁块结构

由于电机边齿倒角和磁块结构都可以对电机纵向磁通进行削弱,降低端部力,抑制电机推力波动。所以本文提出一种新结构,将磁块结构与倒角结构相结合,在边齿处贴上一个近似梯形的磁块结构,最大程度上削弱电机端部力。含梯形磁块结构见图17。

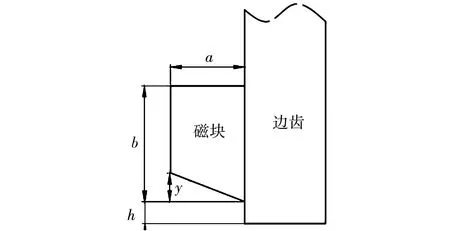
图17 梯形磁块结构

考虑到边齿处磁块优化变量较多,参数化计算较为复杂,本文利用Kriging代理模型与多目标遗传算法结合的优化方法,对多结构参数进行寻优,最大程度削弱端部力,满足电机指标要求。

其优化过程为:

首先确定约束与优化目标:确定4个优化变量的取值范围,明确优化目标推力与推力波动。

其次选取样本空间:利用拉丁超立方试验设计,对4个优化变量进行随机取样,构建样本空间,并用有限元分析计算各样本点的推力与推力波动。

然后构建代理模型:利用已有样本空间构建Kriging代理模型

最后目标寻优,利用多目标遗传算法对优化目标推力与推力波动进行优化收敛,获得pareto解集选择最优参数结构。

1)确定约束与优化目标。

针对磁块上移高度h,磁块长度a,磁块高度b和倒角高度y约束条件为:

(11)

优化目标是保证推力和推力波动满足如下指标要求:

(12)

式中:F为电机平均推力;Fpk2pk为电机推力波动峰峰值。

2)选取样本空间。

本文采用拉丁超立方抽样(Latin hypercube,LH),是一种从多元参数分布中近似随机抽样的方法。样本点选取中设置样本维度为4,样本点为150,对抽样选出的样本点进行有限元计算,计算出电机的平均推力与推力波动峰峰值,为后面的Kriging代理模型的搭建提供数据准备。

3)代理模型搭建。

在150个样本点的基础上,搭建Kriging代理模型,并在此基础上进行优化设计,得到预测更加准确的改进Kriging代理模型,降低模型的预测误差。改进Kriging代理模型流程图见图18。

图18 改进Kriging代理模型流程图

构建代理模型后,选取10个验证点对代理模型的误差进行检验,代理模型检验误差见表6。

表6 代理模型检验误差

由表中数据可知,在经过改进后得到Kriging模型极大程度上降低了原模型的误差,提高了预测精确度。

4)目标寻优。

在改进Kriging代理模型的基础上,利用多目标遗传算法来实现永磁直线同步电机梯形磁块结构的多目标优化。设定初始样本数为4 000,每次迭代样本选取800,经过10次迭代,选取2个最优结构参数。迭代过程见图19,优化结果见表7,表8。

图19 推力波动峰峰值和推力迭代过程

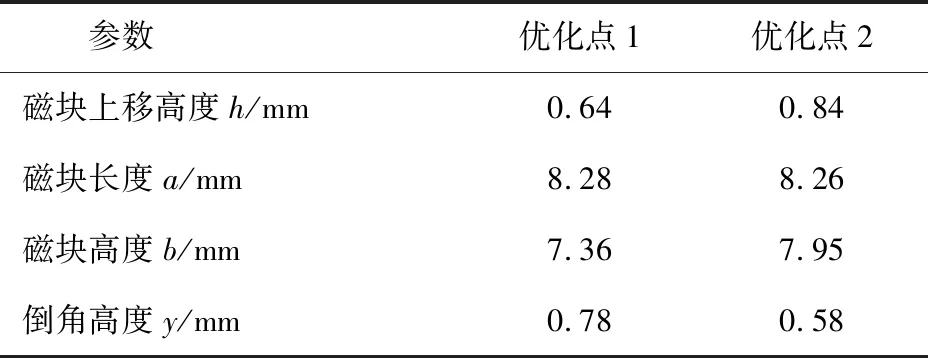
表7 电机最优梯形磁块结构参数

表8 电机优化结果

由表中优化结果可知,针对电机推力,Kriging模型对电机推力的优化准确度很高,误差值几乎可以忽略,电机推力也稳定在2 000 N附近。

针对电机推力波动,误差值也稳定在平均误差之下,最优点推力波动峰峰值也降低到84.15 N。相比于电机初始模型,推力波动削弱了70.2%,推力波动百分比为4.2%,满足电机指标要求。

最后对4种措施进行对比:初级长度优化,倒角优化,端部磁块结构,梯形磁块结构优化数据对比见表9。

对比数据可得,选择梯形磁块结构,推力2 000.2 N,推力波动峰峰值84.15 N,推力波动百分比为4.2%,满足电机性能指标。

5 结 论

本文首先通过实验平台对一台现有样机的磁阻力进行实验,将实验测得空载推力波动数据与仿真值对比,其差值小于2.7%,由此验证了仿真计算的准确性。然后针对11极12槽永磁直线电机推力波动难以达到性能指标要求,从初级长度与端齿结构两方面削弱端部力,降低推力波动,结论如下:

1)针对电机初级角度,利用傅里叶分解,推导出直线电机最优长度计算公式,可计算出电机最优初级长度范围,提高公式通用性。并在此范围内利用有限元仿真进一步优化电机长度,可得电机最优长度为371 mm,推力波动195.7 N,相比于原始电机,推力波动削弱了30.8%。

2)针对端齿结构,分别采用底部倒角结构,端部磁块结构,以及梯形磁块结构,3种方法削弱端部力,降低推力波动,可将电机推力波动分别削弱58.5%、67.9%、70.2%。其中,考虑到梯形磁块结构的多参数的计算复杂性,选用基于Kriging代理模型的多目标遗传算法的优化方案,在满足电机性能指标的基础上可最大程度削弱端部力,降低推力波动。

最后选择梯形磁块结构,推力2 000.2 N,推力波动峰峰值84.15 N,推力波动百分比为4.2%,满足电机性能指标。但是由于磁块为导电物质,在磁场变化下容易引起涡流损耗,可能导致磁块温度过高对电机本体造成影响,需要后续实验进一步分析。