对两道绳、杆连接体问题的深入研究
2023-09-19黄尚鹏
黄尚鹏
(湖北省监利市实验高级中学)
本文先对一道绳连接体问题运用两种方法寻找系统总动能最大时的位置,阐释“保守力学体系在系统的平衡位置势能取极值”这一结论;再对2015年高考全国Ⅱ卷一道杆连接体问题进行定量研究,求出滑块的最大速度和最大加速度以及杆对滑块的作用力随杆与竖直方向的夹角的变化规律,并为本题的定性解答提供理论依据,以体现高考命题的科学性.
1 绳连接体问题的深入研究
1.1 对原题的分析与解答

图1
方法1 矢量三角形法
如图2所示,假设小球A在A'位置时,A、B组成的系统静止,此时轻杆与水平方向成θ角,A'P段的轻绳与水平方向成α角.对小球A、B进行受力分析,小球B受力平衡,轻绳的拉力FT=mg,小球A受重力2mg、轻杆的弹力FN和轻绳的拉力FT的作用,且这三个力平衡,构成一个封闭的矢量三角形.在矢量三角形中,由正弦定理得
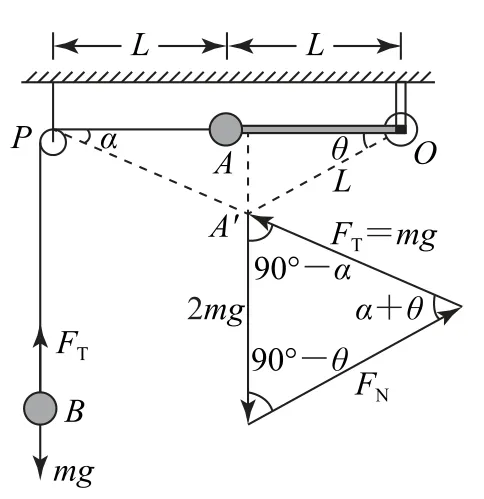
图2
联立式①②,得sinα=cosθ,故α+θ=90°,此时轻绳与轻杆夹角为90°.
将α+θ=90°代入式①,得,故此时轻杆与水平方向的夹角θ=60°.
方法2 正交分解法
如图3所示,对小球A受力分析,由平衡条件得水平方向:竖直方向:
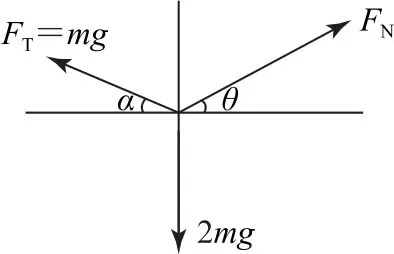
图3
2)寻找系统总动能最大时的位置.
如图4所示,假设小球A运动到A'位置时,轻杆与水平方向成θ角,A'P段的轻绳与水平方向成α角.由机械能守恒定律可知,当系统的总动能最大时,系统的总势能最小,系统势能减少最多,下面我们用两种方法寻找系统总动能最大时的位置.
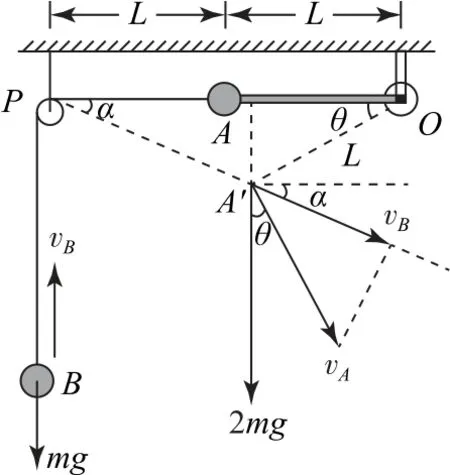
图4
方法1 数学方法
在△POA'中,由余弦定理得
故当轻杆与水平方向的夹角θ=60°时,即在系统静止时的平衡位置,A、B组成的系统总动能最大.
方法2 物理方法
根据重力做功与重力势能变化的关系WG=-ΔEp可知,当系统的重力做正功时,系统的重力势能减少,当系统的重力做负功时,系统的重力势能增加,故当系统的重力总功率为零时,系统势能取极值.或者对系统应用动能定理W合=ΔEk,当系统的合外力做功最多时,系统的总动能增加最多,故当系统的重力总功率为零时,系统的总动能最大.设此时小球A的速度为vA(vA与轻杆垂直),小球B的速度为vB,则
联立式①②③,得sinα=cosθ,故α+θ=90°,此时轻绳与轻杆夹角为90°,即在系统静止时的平衡位置,A、B组成的系统总动能最大.
1.2 总结
1)本题要寻找系统总动能最大时的位置,常规思路是根据机械能守恒定律得出系统总动能的表达式,然后利用数学工具求极值,考查利用数学知识解决物理问题的能力.方法1以θ为自变量,利用导数工具,根据复合函数的导数公式求解,由一阶导数为零求出极值出现的位置.方法2是物理解法,根据“系统的重力总功率为零时系统的总动能最大”这一条件巧解,属于特殊快捷解法,要求考生具有敏锐的洞察力,一般考生难以想到.
2)本题得出系统在静止时的平衡位置总动能最大,这是一种巧合还是必然呢? 其实理论力学中根据分析力学原理可得出这样一个基本结论:保守力学体系在系统的平衡位置势能取极值,本题就是根据这一结论改编而成的.为进一步理解这一思想,笔者再举一个典型例子.如图5所示,半径为r的光滑半球形碗O固定在水平面上,一长度为l、质量为m的均质棒斜靠在碗缘,一端A在碗内,另一端B在碗外,棒静止时与水平方向的夹角为α,试证明:

图5
我们知道如果一个力所做的功与具体路径无关,这种力叫作保守力.在保守力场中,保守力所做的功等于势能的减少.保守力学体系处于平衡状态时势能取极值,根据系统势函数一阶导数为零,可得出系统在保守力以及约束力等作用下的平衡位置,因此此平衡问题也可用能量的观点求解.如图6所示,选碗口所在的水平面为重力势能参考面,则棒的势函数

图6
以α为自变量,对势函数求一阶导数,并令导数为零,寻找平衡位置,即
为验证上述解法是否正确,尝试用其他观点求解本题.如图7所示,对棒进行受力分析,由三力汇交原理知,弹力FN1、弹力FN2和重力mg的作用线相交于一点E.由几何关系得lOA=lOD=lOE=r,∠DOE=2α,∠AEC=90°-2α,∠ACE=90°+α.在△ACE中,由正弦定理得所以有
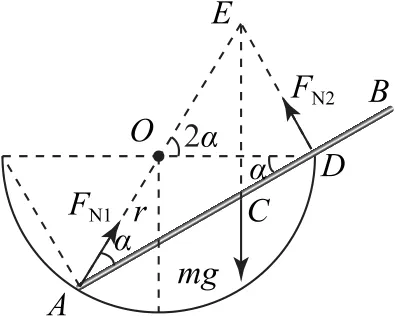
图7
2 杆连接体问题的深入研究

图8
A.a落地前,轻杆对b一直做正功
B.a落地时速度大小为
C.a下落过程中,其加速度大小始终不大于g
D.a落地前,当a的机械能最小时,b对地面的压力大小为mg
2.1 滑块a 落地前,滑块b 的最大速度
为方便起见,我们假设初始时刻轻杆沿竖直方向,杆长为L,由于受到轻微扰动,整个系统由静止开始运动.
如图9所示,设某时刻滑块a、b的速度分别为va、vb,此时刻杆与竖直方向的夹角为θ,根据两滑块沿杆方向的分速度相等得

图9
由系统机械能守恒,得
2.2 滑块a 落地前,滑块a 的最大加速度
如图10所示,由速度矢量三角形得滑块b相对滑块a的速度与两滑块的速度大小关系为

图10
滑块a的a0-cosθ图像是抛物线的一部分,如图11所示,其中当cosθ=2 3时,滑块a的加速度a0=g,这是不难理解的,因为由前面的分析可知,此时b的速度最大,b的加速度为零,杆对两滑块的作用力F=0.
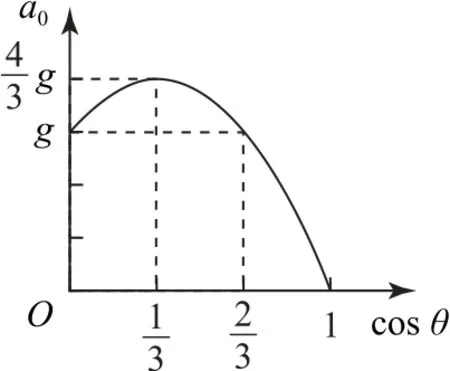
图11
2.3 滑块a 落地前,杆对滑块的作用力F 随杆与竖直方向的夹角θ 的变化规律
如图12所示,设杆对两滑块的作用力为F(下面我们约定用正值表示推力,负值表示拉力),对两滑块受力分析,设地面对滑块b的支持力为FN,在地面参考系中,滑块b在竖直方向处于静止,由平衡条件得

图12
选滑块a为参照系(非惯性系),研究滑块b相对滑块a的运动,为使牛顿运动定律成立,必须引入惯性力,惯性力的大小
滑块b相对滑块a做圆周运动,向心力为指向圆心的合力
3)滑块a的加速度大小,化简得a0=(-3cos2θ+2cosθ+1)g,这与前面得出的结论完全一致.
(完)
