基于个体传染病模型研究个体行为改变对甲型H1N1的影响

闫琴玲, 肖燕妮

(1 长安大学 理学院, 陕西 西安 710064; 2 西安交通大学 数学与统计学院,陕西 西安 710049)

当突发性传染病传播到社区时,个体可以通过改善个人卫生、保持社交距离、服用抗病毒药物、自愿接种疫苗等措施改变自己的行为,从而保护自己免受感染。数学模型可以提供一套强有力的工具来刻画个体行为改变的过程,并已被广泛用于证实非药物干预措施的有效性。为了解人类行为改变如何有助于减缓传染病的传播,研究者对仓室模型进行了研究[1-6]。仓室模型可以反映与传播有关的健康状况(如SIR模型中的易感者、感染者和恢复者)、年龄或其他相关个体特征,并通过单个参数来衡量。但这种建模方法忽略了同一仓室内个体在感染性、敏感性、免疫水平和行为方面的差异。然而,由于计算能力和计算模型的限制,以往的数学模型仅限于研究种群水平上具有行为改变机制的仓室模型[1,4,7-9]。

个体水平的传染病模型(individual behavior models,IBMs)通过个体与其环境之间的相互作用可以揭示个体行为改变对突发性传染病的影响[10]。更具体地说,IBMs可以根据构建的网络结构追踪到每个个体的行为和感染状态[11]。此外,每个个体的特有属性或状态变量,如空间位置、生理特征或社交行为,会随时间而改变[12-13]。因此,IBMs可以用来刻画个体之间的异质性以及相互作用,从而有助于评估实施传染病定向干预措施的有效性。

然而,大多数研究者主要考虑IBMs模拟[14-16],或从网络角度量化真实人群中的异质性[17],很少综合考虑这两种方法[18]。Liu等[19]提出用IBMs刻画公共卫生部门的响应和个体行为改变的模型。此外,文献[20-22]的研究建立了一个基于IBMs斑块网络的动态系统,并将ABC舍选法应用于生态系统模型IBMs的参数估计。 结果表明,ABC方法可以用来对复杂系统进行参数化以及对以稳健方式存在的群体进行动态评估。然而,目前尚无研究者基于IBMs和网络结构,通过结合基于序列蒙特卡罗的近似贝叶斯计算方法(ABC SMC)和观测数据,研究突发性传染病暴发期间个体行为改变对整个疫情趋势的影响。

个体行为改变是突发性传染病传播过程中的重要组成部分,并且对个体和决策者采取相应的干预措施非常重要[1,4,7-9,23-25]。因此,将与疾病信息相关的行为改变嵌入传染病传播模型至关重要。那么,在个体水平上,个体行为改变如何影响突发性传染病暴发期间整个疫情的动态发展成为关键问题。

因此,本文首先搜集到西安市第八医院(陕西省传染病院)报告的甲型H1N1流感(A/H1N1)的新增病例数和累计病例数(如图1所示)。然后,利用个体决策心理模型(LHBM)、社交网络、IBMs以及ABC SMC方法,研究个体行为改变如何影响突发性传染病的动态变化。为刻画个体行为改变对突发性传染病传播的关键作用,将个体的社交网络嵌入HBM模型(记作LHBM)。此外,因为每个个体都有其自身的特点并根据其自身特点做出相应的决策,因此通过对IBMs进行随机模拟来研究个体间的异质性以及相互作用对突发性传染病动态传播的影响。

图1 陕西省2009年9月3日至10月10日A/H1N1病例数Fig.1 The hospital notifications for A/H1N1 during 3rd September to 10th October 2009 in Shaanxi Province

1 基于4种社交网络和A/H1N1的LHBM模型的建立

LHBM模型通过以往经验刻画其与情景信息之间的关系,从而可以用于刻画突发性传染病暴发期间的行为决策。因此,基于Durham等[23]提出的主要观点,引入并介绍LHBM模型之间的4种关系(包括自觉易感性、自觉严重性、自觉障碍和自觉利益)。LHBM模型的详细描述见文献[25]。

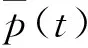
表1 在4种经典的社交网络结构下,模型所有未知参数的均值和标准差的取值范围及其估计值Tab.1 The ranges and the reasonable estimated values of means and standard deviations for all unknownparameters of model with different social networks

图2 基于4种社交网络的LHBM、IBMs与ABC SMC方法相结合的流程图Fig.2 The scheme of the LHBM and IBMs combining with ABC SMC methods based on social networks

2 基于ABC SMC方法的IBMs参数估计与模型拟合

2.1 基于社交网络的IBMs的建立

为了解在社交网络中突发性传染病的传播机制,考虑到个体之间的异质性和相互作用,我们需要发展IBMs。它可以刻画在每个状态给定的条件下,每个个体是易感者、感染者或恢复者的概率。更具体地说,IBMs通过在个体水平上考虑社交网络结构、异质性和个体之间的连接模式建立模型,可以研究疫情的动态变化[15]。因此,本节使用基于网络的IBMs,在受突发性传染病A/H1N1大规模影响的社区中,模拟个体之间的相互作用。

首先,为刻画传染病传播过程发生的感染事件及恢复事件,我们建立IBMs。然后,由经验及文献[25]可知,每个易感个体都可能受到周围信息环境的影响(例如有关该种传染病的媒体报道量、医院报告的新增病例数、接触的人数、与他人的亲密关系以及个体之间的距离等),并且可以用个体行为改变pi(t)来刻画。此外,基于文献[25]中的模型选择结果,我们将行为改变率以指数函数形式嵌入发病率中。因此对于易感个体i,传播率(或感染强度)定义为

βi(t)=βe-αpi(t)。

(1)

式中:β是基线传播率;pi(t)是个体i在第t天的行为改变率;α为校准常数。

对于感染个体j,我们假设其恢复不受周围环境影响,因此感染个体j的恢复率定义为

γj=γ。

(2)

由于人们生活作息习惯以天为周期,从而本文模型中以天为单位。因此,根据文献[26],事件率φ和概率P之间的关系可表示为

P=1-eφ·Δt。

(3)

从而得到在IBMs中,到下一个事件发生所需要的时间

(4)

式中:R1和R2是从均匀分布U(0,1)中产生的随机数;βi和γj是个体的传播率和恢复率;分母部分表示只有感染和恢复两个事件发生。

因此,如果不等式

(5)

成立,则将发生感染事件,否则发生恢复事件[26]。此外,网络在考虑个体之间的相互影响方面发挥着重要作用。 当每个个体只与少部分人直接接触时,这些方法尤其有效[27]。再者,由于他们的社交接触,通过网络我们可以很好地了解个体感染的传播机制。因此,基于网络的IBMs可以在一个简单的框架中刻画个体水平复杂的结构[28]。

此外,考虑到计算成本、计算复杂度,且为使残差绝对值的和最小,我们选择规则网络来模拟IBMs中的网络(见表1)。我们用一个连接矩阵(G=(Gij),如果个体i和j有连接,则Gij为1,否则为0)刻画网络中所有接触到的个体,由规则网络的特性和A/H1N1的传播特点可知,该矩阵为稀疏矩阵。如果要对以上模型进行模拟,需要给定参数α、β和γ的值,而实际中参数的取值往往是未知的。因此,下面基于观测数据,将IBMs和ABC SMC方法相结合来进行参数估计和模型拟合。

2.2 IBMs参数估计与模型拟合

ABC SMC方法是在不计算似然函数解析表达式(基于数据,依赖于模型参数)的情况下,通过多次对模型进行模拟来近似估计参数的后验分布[29]。因此,我们利用ABC SMC方法,对IBMs进行参数估计和模型拟合。

(6)

此外,我们用模拟的累计病例数与观测数据之间的平方和除以观测数据的平方(相对残差平方和RRSS,记作SRRS)来计算拟合优度,即

(7)

基于上述IBMs和ABC SMC算法,参数估计和模型拟合结果分别如图4b和图5a所示。图4给出了参数α、β和γ后验分布的箱型图,包括最大值、上四分位数、中位数、下四分位数、最小值和95%置信区间。

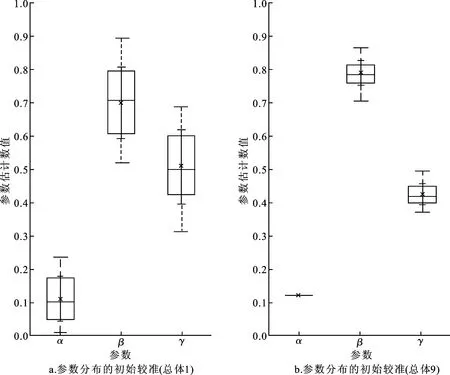
图4 参数α、β、γ的分布Fig.4 Distributions of parameter α,β and γ注:网络版为彩图。星号表示中位数,绿线部分表示95%置信区间。方框图包括最大值、上四分位、中位数、下四分位和最小值。

图5 基于IBMs、规则网络以及ABC SMC的参数估计结果拟合累计病例数及参数α、β、γ的模型随机性结果Fig.5 Fits of IBMs with regular networks for the number of accumulated infected individuals based on the parameter values of ABC parameter estimation and the stochastic results of model of the parameter α,β,γ注:黑圈是观测数据,黑线是平均值,阴影区域是总体9的100次模拟结果的均值±标准差。

通过将图4a与4b进行比较,易知: 通过再校准,数据对所有参数的后验分布提供有用的信息,从而使得参数估计结果更准确,特别是参数α。

当选择总体9时,图5a给出了9月3日至10月10日模拟的平均累计病例数和区间(平均值±标准差,分别为黑线和阴影区)所示。很明显,模型拟合很好,并且所有观测值在区间(平均值±标准差)内。拟合优度为3.35%,这也说明模拟的平均累计病例数对观测数据拟合效果很好。

3 敏感性分析

为研究模型随机性、ABC重新校准不确定性以及其他(未校准)参数初始校准不确定性的影响,我们利用IBMs分析参数α、β和γ的不确定性,并对每组参数随机模拟100次[29]。首先,我们从其后验分布众数(总体9)中抽取再校准参数,并将其他参数固定到其初始校准平均值(总体1),从而得到了模型随机性的影响。其次,从其后验分布(总体9)中抽取再校准参数,并将其他参数固定到初始校准平均值(总体1),探讨模型随机性和ABC再校准不确定性共同作用的影响。最后,从其后验分布(总体9)中抽取再校准参数,从与初始校准相对应的均值和标准差的正态分布中抽取其他参数(总体1),研究模型随机性、ABC再校准不确定性以及初始校准不确定性的共同影响。其中,上述参数的抽样方法采用的是拉丁超立方体抽样(Latin hypercube sampling,LHS)方法。

上述3个参数的模型随机性结果如图5b～d所示,其给出了上述重新校准参数变化对模拟的累计病例数的影响。由图可知: 所有参数对模拟的累计病例数都有很大影响,尤其是β。此外,与图5a中的SRSS相比,SRSS减少(增加)1.37%(5.15%、1.84%),这是因为通过对接触传播率β(校准常数α,恢复率γ)进行了再校准,从而进一步说明个体行为改变对突发性传染病疫情有影响。

为探讨个体行为改变对突发性传染病的影响,我们假设个体行为变化率pi(t)分别下降50%和100%,则到10月10日,模拟的平均累计病例数分别增加2.11%和8.56%。 然而,如果个体的行为改变率pi(t)增加25%和50%,则到10月10日,模拟的平均累计病例数将分别减少1.89%和7.56%,如图6所示。以上结果表明:个体行为改变率会显著影响医院报告的累计病例数。

图6 基于ABC参数估计的参数值,进行个体行为改变率对IBMs的敏感性分析Fig.6 The sensitivity analyses of IBMs with respect to the individuals’ rate of behavior change based on the parameter values for the ABC parameter estimation注:黑圈为观测数据,黑线为均值,阴影区为总体9的100次模拟结果的均值±标准差。

4 结语

基于IBMs的研究表明,在传染病传播过程中,随着随机性越来越大,基于观测数据对其进行参数化在统计计算上也越具有挑战性。然而,ABC SMC已经作为一种有效的方法被广泛应用于群体模型的参数推断[25,30]。因此,我们将IBMs、ABC SMC与个体行为改变有效结合来研究个体行为改变对疫情的影响,从而可以提升公共卫生控制策略,加强突发性传染病的缓解措施。本文的创新之处在于:首先,为更加准确地刻画个体行为改变的影响,我们实现了不同模型在个体水平上与个体行为改变率的耦合。其次,我们通过ABC SMC方法实现了IBMs的参数估计和模型拟合,这是在突发性传染病研究方面的首次尝试。再次,我们在LHBM中模拟了个体决策和4种社交网络,然后将个体行为改变率以指数函数的形式嵌入到基于社交网络的IBMs发病率中,研究了个体行为改变对2009年陕西省A/H1N1流感疫情的影响。

我们应用一种基于社交网络的IBMs来刻画传染病传播过程中个体间的异质性和相互作用,该模型对模拟传染病暴发的趋势具有一定的指导意义。采用ABC SMC方法进行参数估计、模型拟合以及敏感性分析,结果表明: 所有参数,特别是β,对模拟的累计病例数都有很大影响; 模型随机性、ABC再校准不确定性和初始校准不确定性的共同作用降低了参数估计的误差,提高了对观测数据的拟合; 个体行为改变率的变化会显著影响报告的累计病例数。

敏感性分析发现,个体行为改变对疫情初期感染人数的影响不大,但对后期感染人数的影响很大。其可能有两方面原因: 一方面,行为改变影响的延迟可能是A/H1N1感染的潜伏期和应对突发性传染病暴发所需要的行为改变时间引起的;另一方面,在2009年A/H1N1等突发性传染病暴发时,感染病例数量较少,行为改变的影响不明显。然而,初期过后,随着感染病例迅速增加,人们开始采取相应的保护措施,因此个体行为改变对传染病后期的发展具有重要影响。

我们的研究有以下两个局限性。首先,考虑所提出的所有网络会增加计算成本和复杂性,我们应用ABC SMC方法仅对基于规则网络的IBMs进行随机模拟和参数估计。 其次,由于计算量大,模型拟合不太理想,因此有必要对算法和研究方法进行改进。

综上,本文通过建立LHBM,把个体行为改变率的函数以指数形式嵌入IBMs中,再利用ABC SMC方法推断IBMs中参数的后验分布并进行模型拟合。研究表明: 将ABC SMC和IBMs相结合有助于分析行为改变对突发性传染病暴发的影响,而且个体行为改变率的变化会显著影响医院报告的累计病例数。因此,媒体宣传应集中在如何引导个体的行为改变,而且个体的积极响应对于突发性传染病的缓解和控制至关重要。