分相级联大容量高压直流变压器拓扑及控制策略

吴小丹，殷子寒，朱海勇

（1.南京南瑞继保电气有限公司，江苏省 南京市 211102；2.南瑞集团有限公司（国网电力科学研究院有限公司），江苏省 南京市 211106）

0 引言

发展以风电及光伏为主体的新能源系统，是实现中国“碳达峰·碳中和”目标的一项重要手段［1］。目前，实现大规模新能源接入和送出主要通过高压交流输电系统和柔性直流输电系统［2-4］。近年来，采用柔性低频输电系统的海上风电送出也成为学术界和工业界的研究热点［5-6］。

在传统交流接入方式中，通过升压接入高压交流系统，但交流系统固有的对地电容过大现象会导致输送的有功功率受到限制，这一现象在大容量、远距离的集中式新能源送出场合尤为显著。基于模块化多电平换流器（modular multilevel converter，MMC）的柔性直流输电系统送出可有效解决传统交流送出方案存在的上述问题，从而得到广泛应用。然而，基于MMC 构建的交流系统和新能源逆变器为主体的系统之间存在较为复杂的功角及电压等稳定性问题，在故障过程中还存在直流故障电流难以切除及负序电流抑制等一系列复杂难题［7-8］。

因此，基于全直流系统的新能源送出方案得到了广泛关注［9-11］。在该方案中，以各级直流变压器（direct current transformer，DCT）为核心设备构建的直流系统可实现新能源系统的汇集及送出，并经过直流-直流变换直接接入柔性直流输电等汇集系统。显然，整个直流送出系统中不存在相位、功角、频率及负序等问题，可大幅度提高成套系统的稳定性及可靠性。此外，相比工频变压器，在DCT 中采用中频变压器进行交流部分的隔离可有效降低变压器的体积和重量，进一步降低直流变压器功率模组直流电容的容值，有效提升DCT 能量密度，从而实现减小成套系统占地面积和总体投资的目的［12］。因此，开展基于全直流方式下新能源送出方案的相关研究，具有重要的现实意义和工程应用价值。

高压大容量DCT 是实现全直流送出的关键设备，也是实现电能有效变换的基础。目前，主流的DCT 拓扑有晶闸管谐振型拓扑［13］、双有源型拓扑［14-16］、有源桥和晶闸管等混合型拓扑［17-18］以及基于MMC 的组合式拓扑等［10，19］。在具体的组合方式上，又有输入并联输出串联（IPOS）等4 种方式［20］。在高压大容量应用场合，可满足功率双向传递的主要是基于MMC 型的拓扑，文献［10］给出了基于MMC 带隔离和非隔离的典型DCT 拓扑，并给出了对比分析。文献［10，21-22］提出了基于单相MMC的隔离型DCT 及控制策略。该拓扑具有一定成本优势，而和单相电力电子变换器拓扑类似，该拓扑存在中频二倍频电流波动流入直流侧的潜在风险［23］。文献［22，24］提出了基于三相MMC 的隔离型DCT，但是该拓扑的高压侧对功率器件数目需求较多，其占地和成本仍不可忽视。面向未来满足全直流大容量新能源送出工程应用的现实需求，实现百兆瓦级的大容量换流、降低单相MMC 型直流侧二倍频电流注入、实现中高压直流侧能量双向传输、满足换流阀轻量化及减少占地等一系列现实需求仍应在实际应用中予以克服。

为此，本文提出了一种适用于高压大容量应用场合且可实现电能双向传递的DCT 拓扑，其高压侧采用基于半H 桥的3 个单相MMC 级联的方式，中压侧采用三相MMC 形式，并通过中频变压器进行隔离［25］。该拓扑具备良好的电能输出质量且对功率器件的需求较少。然后，提出了实现高、中压侧完全解耦的控制方案。在高压侧，通过5 个层级的逐级层次化控制实现高压侧3 个级联单相MMC 桥臂功率模组直流侧电容电压的完全稳定。在此基础上，通过V/f闭环控制构建400 Hz 中频系统以实现高压和中压直流间的能量转换。中压侧三相MMC则通过dq旋转坐标系统下的正、负序双闭环控制，并附加静止坐标系统下的桥臂环流抑制实现中压侧输出直流电压的稳定。最后，搭建电磁暂态仿真模型，并通过稳态、动态及暂态仿真全面验证所提拓扑及控制策略的有效性和可行性。

1 分相级联高压直流变压器拓扑及控制要求

1.1 分相级联高压直流变压器拓扑

图1 给出了所提分相级联高压直流变压器的拓扑结构。其中，各子模块（SM）均采用半H 桥结构。高压侧通过3 个单相MMC 串联而成，从而满足接入高压柔性直流输电系统的需要，各单相MMC 输出的交流端口接入中频交流变压器，中频变压器降压后接入中压三相MMC。

图1 分相级联高压直流变压器拓扑Fig.1 Topology of split-phase cascaded high-voltage DC transformer

为便于分析，图1 中直流变压器高压侧3 个单相MMC 分别定义为HMMC1、HMMC2、HMMC3。HMMCi（i=1，2，3）的4 个桥臂电流分别为ipai、inai、ipbi、inbi，HMMCi桥臂xy(x=p，n；y=a，b)的第j号功率模块的电容电压表示为udc，xyij(j=1，2，…，N)，其中，N为高压侧各桥臂功率模组的数目。其余桥臂功率模组电容电压定义类似。高压侧各MMC 输出的交流电压分别为uhA、uhB、uhC，流入高压侧MMC的三相交流电流分别为ihA、ihB、ihC；高压侧MMC 桥臂电感为Lh；高压侧直流母线电压为uhd，流出高压侧直流母线的电流为ihd；经过中频变压器后的中压侧MMC 交流电压分别为umA、umB、umC，流入中压侧MMC 的三相交流电流分别为imA、imB、imC；中压侧MMC 的6 个桥臂电流分别为ipAm、inAm、ipBm、inBm、ipCm及inCm；中压侧MMC 桥臂电感为Lm；中压侧直流母线电压为umd，流入中压侧直流母线的电流为imd。

1.2 性能及经济性对比分析

重点对比分相级联MMC 型DCT、附录A 图A1 所示三相MMC 型DCT 及附录A 图A2 所示单相MMC 型DCT。3 种典型拓扑的主要性能及经济性对比如表1 所示。表中：nh和nm分别为所提DCT拓扑高压侧和中压侧单个桥臂模块数目；IGBT 表示绝缘栅双极型晶体管。

表1 基于MMC 拓扑的DCT 性能及经济性对比Table 1 Performance and economic comparison of DCT based on MMC topology

由表1 可见，相比附录A 图A1 给出的三相MMC 隔离型DCT，所提拓扑在高压侧可减少约1/3 的功率器件，换流阀的成本优势明显。而相比附录A 图A2 给出的单相MMC 隔离型DCT 存在的二倍频波动现象，所提拓扑则可实现三相中频交流功率在高压及中压直流侧送入及送出侧的自平衡，在未来工程应用中无须考虑在高压及中压侧设置高频滤波器以滤除二倍中频谐波电流的问题。

对中频变压器，由后续章节分析及仿真可见，该变压器3 个独立绕组间均耐受差模中频交流电压，因此，其三相绕组磁设计等可沿用常规变压器的设计方法。而通过适当增强变压器三相绕组对地及绕组间的绝缘能力，即可满足中频变压器三相绕组对地存在的直流电压偏置要求。此外，综合考虑中频变压器体积、重量、损耗及DCT 中频侧控制保护系统对频率的要求［22］，本文选取中频频率为400 Hz。

综上所述，所提分相级联高压直流变压器可以兼顾高性能及良好的经济性，未来具有显著的工程应用前景。

1.3 分相级联高压直流变压器控制要求

为实现图1 所示的直流变压器在控制上的完全解耦，将控制策略分别设计为高压侧控制及中压侧控制，且确保两侧控制之间没有强关联性。

1.3.1 高压侧控制要求

为实现高压侧3 个单相MMC 桥臂直流侧电压的稳定，提出5 个层级的均压策略。通过逐级控制，实现高压侧3 个单相MMC 各桥臂功率模组电容电压的完全稳定。

高压侧第1 层控制通过从高压直流母线吸收有功直流电流ihd，实现高压侧3 个单相MMC 所有桥臂功率模组电容电压总和的稳定；高压侧第2 层控制在第1 层控制稳定的基础上，通过调节3 个MMC 桥臂输出电压的共模直流分量Δuhbg，i来微调各MMC间的有功功率，进而实现各MMC 间桥臂功率模组电容电压总和的均衡；高压侧第3 层控制在第1、2层控制稳定的基础上，通过调节各MMC 桥臂内的直流环流Δihdcciry，i实现其A 相（含有pa 及na 桥臂）和B 相（含有pb 及nb 桥臂）2 个桥臂间功率模组电容电压的均衡；高压侧第4 层控制在第1 至3 层控制稳定的基础上，通过调节各MMC 桥臂内的中频交流环流Δi′haccirxy，i实现其A 相和B 相各自上、下桥臂间功率模组电容电压的均衡；高压侧第5 层控制在第1 至4层控制稳定的基础上，通过桥臂内的均压控制实现桥臂内各功率模组电容电压的均衡。

通过所设计的5 层均压控制策略，可以实现高压侧3 个单相MMC 所有桥臂功率模组电容电压的完全均衡。此外，在设计第3、4 层均压控制策略时，需确保注入的环流分量不流入直流变压器的高压直流母线及高压中频交流侧，从而确保高压侧桥臂均压控制的完全解耦。

在高压侧3 个单相MMC 功率模组电容电压完全稳定的基础上，通过V/f开环或闭环控制实现高压侧中频电压uhA、uhB、uhC的稳定输出，中频变压器进而感应出中压侧中频电压umA、umB、umC。

1.3.2 中压侧控制要求

由于中压侧MMC 为三相拓扑结构，三相交流输入侧采用dq旋转坐标系统下的控制方法。此外，为实现对桥臂环流的抑制，本文采用静止坐标系统下的桥臂电流直接控制策略。

通过高、中压侧的控制，可实现高压直流至中压直流的转换，从而满足中压侧光伏等直流设备接入的需求。同时，也可以满足高压侧向中压侧供电的需求，即实现有功潮流的双向流动。

2 控制策略的提出及实现

以下分别对所提拓扑的控制策略作出具体说明。

2.1 高压侧控制策略

图2 给出了分相级联直流变压器高压侧的控制框图。其中，V/f控制采用闭环控制策略。

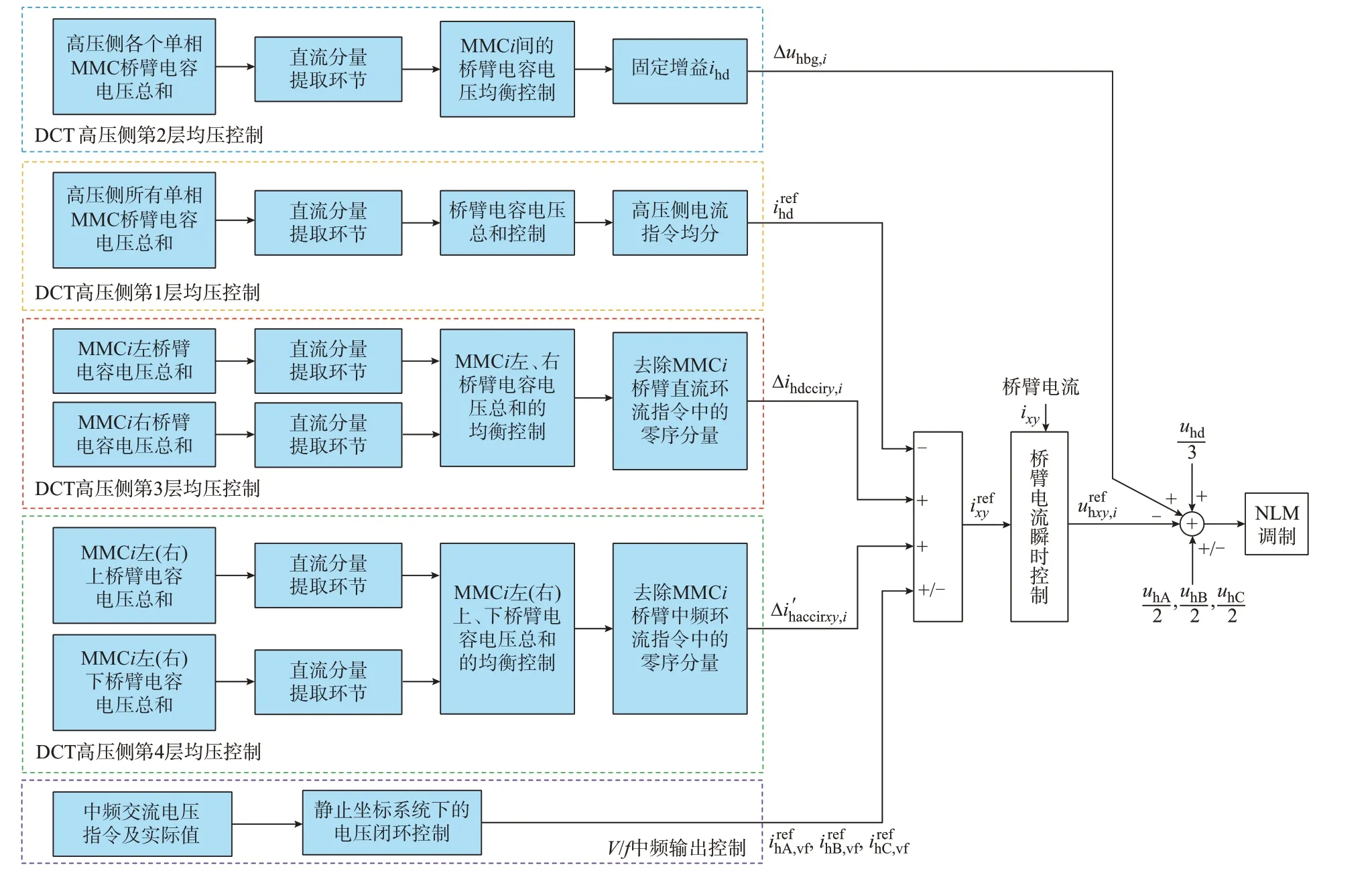
图2 直流变压器高压侧控制策略Fig.2 Control strategy of DC transformer on high-voltage side

2.1.1 高压侧第1 层控制

第1 层控制需实现高压侧3 个单相MMC 所有功率模组电容电压的稳定。将高压直流母线视为电源，通过从高压直流母线注入直流电流ihd实现这一目标。

假定高压侧3 个单相MMC 所有功率模组电容电压总和为uhdc，1，在直流变压器处于稳定状态后可得：

式中：C为高压侧功率模组电容容值。

根据小信号分析法，在稳态工作点附近作局部线性化，且视中频交流侧输出有功功率为扰动，去除式（1）中的更高阶分量后可得：

式中：Uhd为高压侧直流电压的稳态值；Uhdc，1为高压侧3 个MMC 所有桥臂功率模组电容电压总和的稳态值；Δihd、Δuhdc，1分别为ihd、uhdc，1在稳态运行工作点附近对应的变化值。

根据式（2），可得到高压侧直流输出电流ihd的控制参考值在时域系统中的控制方程为：

式中：kdc，p1和kdc，i1分别为第1 层控制器的比例、积分参数；为高压侧3 个MMC 所有功率模组电容电压总和的指令值。

本层闭环控制框图如附录A 图A3（a）所示。同时由式（3）可见，第1 层比例-积分（PI）控制器呈现导纳性质。

2.1.2 高压侧第2 层控制

由于各MMC 均流过高压侧直流电流ihd，如图3（a）所示，通过调节各MMC 桥臂输出电压中的直流共模分量Δuhbg，i，并和ihd耦合产生有功功率，进而调节3 个单相MMC 间的有功平衡。

图3 高压侧第2 至4 层均压控制框图Fig.3 Block diagram of voltage equalization control for the 2nd to 4th layers at high-voltage side

假定为满足本层控制目标，控制单相MMCi桥臂输出电压中共模直流分量的变化量为Δuhbg，i，且由此导致的高压侧各MMC 的4 个桥臂电容电压总和的变化量为Δuhdcall，i。由功率守恒关系可得：

式中：Uhdcall，i为高压侧MMCi的4 个桥臂功率模组电容电压的总和，在稳态情况下应为Uhdc，1的1/3。

第1 层控制确保了3 个单相MMC 桥臂电容电压总和的稳定。因此，本层控制只需确保Δuhdcall，i间保持一致。定义高压侧MMC 桥臂电容电压总和的平均值uhdcall，avg为：

式中：uhdcall，i为HMMCi的4 个桥臂功率模组电容电压的总和。

根据式（4）、式（5），为确保本层控制不影响第1层控制，可得本层控制在时域系统中的控制方程为：

式中：kdc，p2和kdc，i2分别为第2 层控制器的比例、积分参数。

本层闭环控制框图如附录A 图A3（b）所示。同时由式（6）可见，第2 层PI 控制器呈现标幺特性。

2.1.3 高压侧第3 层控制

第3 层控制需实现各MMC 左、右2 个桥臂功率模组电容电压总和的均衡。由于3 个单相MMC 控制策略一致，以HMMC1 的环流控制为例进行说明。

如图3（b）所示，控制桥臂内附加直流环流Δihdccira，1和Δihdccirb，1使得该环流和左、右2 个桥臂输出电压中的稳态直流分量uhd/3 耦合产生有功功率，进而调节左、右桥臂间的功率平衡。假定由Δihdccira，1、Δihdccirb，1导致的HMMC1 左、右桥臂功率模组电容电压总和的变化量分别为Δuhdca，1、Δuhdcb，1，则根据能量守恒定律可得：

式中：Uhdcy，i(y=a，b)分别为HMMCi左、右2 个桥臂功率模组电容电压的总和，在稳态情况下Uhdca，i、Uhdcb，i应相等且为Uhdcall，i的1/2。

同时，本层控制产生的直流环流应只在各个MMC 内部流通而不流入中频交流侧及直流侧，从而确保本层控制不影响第1、2 层的控制。根据式（7），可得到时域下的控制方程为：

式中：uhdca，i和uhdcb，i分别为HMMCi左、右桥臂功率模组电容电压的总和；kdc，p3和kdc，i3分别为第3 层控制器的比例、积分参数。

本层闭环控制框图如附录A 图A3（c）所示。同时由式（8）可见，第3 层PI 控制器呈现导纳特性。

2.1.4 高压侧第4 层控制

第4 层控制需实现各MMC 上、下2 个桥臂功率模组电容电压总和的均衡。对HMMC1 而言，需实现pa 和na 桥臂以及pb 和nb 桥臂间的功率均衡。以实现HMMC1 桥臂pa、na 间功率均衡为例，假定HMMC1 桥臂pa、na 功率模组电容电压总和分别为uhdcpa，1、uhdcna，1。如图3（c）所示，控制桥臂内附加中频环流为Δihaccira，1，使得该环流和中频交流输出相电压0.5uhA耦合产生有功功率，进而调节桥臂pa、na 间的功率平衡。假定由Δihaccira，1导致的桥臂pa 电容电压波动为Δuhdcpa，1，则根据桥臂功率平衡原则可得：

式中：Vh为中频变压器高压侧相电压峰值；ΔIhaccira，i为流经桥臂pa 中频环流的峰值；Uhdcpa，i为桥臂pa 功率模组电容电压的总和，在稳态情况下应为Uhdca，i的1/2。

根据式（9），可得到时域下的电流控制方程为：

式中：kdc，p4和kdc，i4分别为第4 层控制器的比例、积分参数；uhdcpa，i和uhdcna，i分别为HMMCi的A 相上、下桥臂功率模组电容电压总和。

由于本层控制产生的环流为中频交流分量，因此，需将式（10）产生的电流指令值转换为瞬时值。同时，为保证调节桥臂pa、na 功率平衡过程中产生的中频环流不流入中频交流侧，则HMMC1 桥臂pa、na 的中频环流Δihaccirpa，1和Δihaccirna，1应为：

式中：θhA为直流变压器高压侧输出A 相电压的锁相环角度。

同样，推导过程适用于桥臂pb、nb 的中频环流指令Δihaccirpb，1和Δihaccirnb，1，表示为：

式中：ΔIhaccirb，1为对HMMC1 的pb、nb 桥臂进行均压控制产生的中频环流指令，计算过程类似式（10），不再赘述。

为同时满足本层控制的环流不流入高压直流侧及高压交流侧的目标，需进一步对式（11）、式（12）产生的中频环流指令做进一步修正。首先，求取pa和pb 两个上桥臂及na 和nb 两个下桥臂的零序电流指令Δihaccirp0，1和Δihaccirn0，1如下：

将式（11）、式（12）产生的中频环流指令减去式（13）给出的零序分量，即可得到HMMC1 桥臂pa、pb、na、nb 经过修正后的中频环流指令为：

对HMMC2、HMMC3 的pa、na 桥臂的均压控制以及pb、nb 桥臂的均压控制过程类似，不再赘述。

可以验证，式（13）、式（14）给出的中频环流指令可同时满足不流入高压直流侧及中频交流侧，而仅在各单相MMC 内部流通的要求。

本层闭环控制框图如附录A 图A3（d）所示。同时可见，第4 层PI 控制器呈现导纳特性。

2.1.5 高压侧第5 层控制

如前所述，第5 层控制需实现各MMC 各桥臂内功率模组电容电压的均衡。本文采用最近电平逼近法（NLM），实现过程不再赘述。

2.1.6 高压侧中频交流输出V/f闭环控制

为实现中频变压器输出交流电压的稳定，采用自产锁相环下的V/f闭环控制产生uhA、uhB、uhC。控制目标为产生各HMMCi桥臂中的中频电流指令。

由于所提拓扑高压侧为分相级联型，3 个单相MMC 输出中频交流电压互相独立且相位互差120°。因此，采用静止坐标系统下的闭环控制以实现3 个单相中频交流电压的稳定运行。以HMMC1控制建立A 相中频交流电压为例，其控制输出电流参考值在时域的控制方程为：

HMMC2、HMMC3 通过V/f闭环控制建立B、C 相中频交流电压的控制过程类似，不再赘述。

2.1.7 高压侧HMMC 电流指令生成

如前所述，高压侧3 个单相MMC 的电流指令由4 个部分组成：1）由2.1.1 节闭环产生的直流电流；2）由2.1.3 节闭环产生的直流环流；3）由2.1.4 节闭环产生的中频环流；4）由2.1.6 节V/f闭环产生的中频输入电流。

对HMMC1 而言，桥臂pa、na、pb、nb 的电流指令可表示为：

对HMMC2 及HMMC3 的桥臂电流指令生成过程完全类似，不再赘述。

2.1.8 高压侧HMMC 桥臂电压参考值生成

由2.1.7 节可知，桥臂电流同时含有直流及中频交流分量。为便于控制，本文采用静止坐标系统下的桥臂电流瞬时值控制策略。

以HMMC1 桥臂pa 为例进行分析，其电路及对应的控制策略如图4 所示。图中：Gc（s）为桥臂电流控制器，由于桥臂电流同时含有直流分量及中频分量，Gc（s）可使用比例控制器为HMMC1 的pa桥臂输出电压指令的参考值。

图4 高压侧桥臂瞬时控制策略Fig.4 Instantaneous control strategy for bridge arm on high-voltage side

根据MMC 桥臂的投切规则，并考虑叠加第2层控制输出，得到HMMC1 桥臂pa、na、pb、nb 的电压参考值的闭环控制方程为：

HMMC2 及HMMC3 的桥臂电压控制方程类似，不再赘述。

2.2 中压侧控制策略

在完成直流变压器的高压侧控制后，中频变压器的中压侧将会感应出中压中频电压。而中压侧为三相MMC 结构，本文采用正、负序下的经典双序闭环控制［26］，如图5 所示。图中为三相中压MMC直流母线电压参考值为三相中压MMC 正序电流参考值；umdp、umqp分别为umz（z=A，B，C）中正序分量对应的d、q值；umdn、umqn分别为umz中负序分量对应的d、q值；imdp、imqp分别为imz中正序分量对应的d、q值；imdn、imqn分别为imz中负序分量对应的d、q值；θpll，m为对umz中正序分量进行锁相得到的角度；Gi（s）为电流内环控制器；ωm为中压侧系统的角频率；icir，pA为桥臂pA 的环流；Gi，cir（s）为桥臂环流控制器；(x=p，n；z=A，B，C)为桥臂xz环流控制输出；和(z=A，B，C)分别为中压侧MMC 三相桥臂正、负序电压参考值。图5 中，将正序q轴无功电流指令设置为0，以保证中频侧输出为功率因数状态。同时，通过负序电流控制将中频侧输出负序电流控制为0。此外，为抑制桥臂环流带来的附加损耗，采用静止坐标系统下的直接控制将环流抑制为0。Gi，cir(s)采用比例控制器，控制框图如图5（c）所示。6 个桥臂的环流icir，xz(x=p，n；z=A，B，C)可表示为：

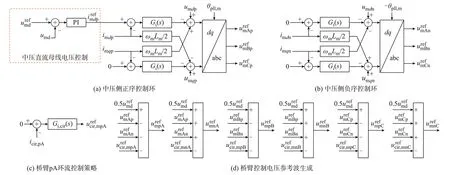
图5 中压侧闭环控制框图Fig.5 Block diagram of closed-loop control on medium-voltage side

采用比例控制器并设置一定的带宽即可满足对中压侧MMC 桥臂环流的有效抑制。将图5（a）正序控制环输出、图5（b）负序控制环输出及图5（c）的桥臂环流抑制环输出按照图5（d）进行综合，即可得到中压侧三相MMC 的6 个桥臂电压控制参考值。

3 仿真验证

3.1 仿真设置

通过PSCAD/EMTDC 验证所提直流变压器拓扑及控制策略的有效性，仿真接线如图1 所示。直流变压器的高压侧接入±200 kV 柔性直流输电系统高压母线，经直流变压器转换后生成±20 kV 中压母线。中频变压器额定相电压的变比为57 kV/12 kV，频率为400 Hz。仿真中±20 kV 侧接入共计4 组光伏，每组光伏系统额定功率为24 MW，各组光伏通过最大功率点跟踪（MPPT）控制后经Boost 变换器升压为1.5 kV，并经1.5 kV/40 kV 升压后接入直流变压器所构建的中压母线。直流变压器中压侧MMC 控制为功率因数模式，直流变压器参数见附录B 表B1。

3.2 仿真结果

分别通过稳态、动态及暂态仿真验证所提拓扑及其控制策略的有效性。

3.2.1 稳态运行仿真

控制光伏系统向DCT 送入有功功率96 MW。图6 给出了稳态下的仿真波形。

图6 稳态运行仿真波形Fig.6 Simulation waveforms in steady-state operation

图6（a）和（b）分别为DCT 的高压直流侧输入电压和中压直流侧输出电压。由图6（a）和（b）可见，中压侧输出正、负极之间电压为40 kV，稳态运行下输出电压稳定。图6（c）和（d）分别为DCT 的高压侧直流输出电流和中压侧直流输入电流。由图6（c）和（d）可见，高、中压侧直流电流稳定，满足设定的输出有功功率要求。

图6（e）和（f）分别为DCT 的高压侧三相输出电压和三相输入电流。图6（g）和（h）分别为DCT 的中压侧三相输出电压和三相输入电流。由图6（e）和（g）可见，中频变压器两侧中频交流电压稳定，频率为400 Hz。由图6（f）和（h）可见，中频变压器两侧电流稳定且保持为单位功率因数运行状态。

图6（i）为DCT 高压侧3 个单相MMC 在a1、a2、a3点的电压波形。图6（j）为DCT 高压侧3 个单相MMC 在b1、b2、b3点的电压波形。由图6（i）可见，a1、a2、a3点电压分别存在200/3、0、-200/3 kV 的直流偏置，而由图6（j）可见，b1、b2、b3点电压存在的直流偏置完全类似。这一点符合预期和设计要求，即传递至中频变压器中压侧的交流电压为无直流分量的差模电压。

图6（k）为DCT 高压侧HMMC1 桥臂pa、na、pb、nb 的电容电压平均值波形。图6（l）为DCT 高压侧HMMC1桥臂pa、na、pb、nb的电流波形。由图6（k）可见，HMMC1 桥臂电容电压平均值稳定在控制系统设定的2.1 kV，均压特性良好且波动以400 Hz 的中频率为主。由图6（l）可见，HMMC1 桥臂电流中同时存在直流及中频分量，且在正常运行时，其环流成分较小。由图6（k）、（l）可见，单相MMC 中处于斜对角位置桥臂的电流和电容电压波动一致，例如桥臂pa 和桥臂nb 电流完全一致，其电容电压波动也完全一致。而上、下桥臂的电流和电容电压波动反相，例如，桥臂pa 和桥臂na 电流和电容电压波动相位互反180°。这些特点均符合单相MMC 桥臂运行特征。

3.2.2 动态运行仿真

为验证所提DCT 拓扑及控制策略在功率动态阶跃下的控制性能，控制光伏系统向DCT 送入的有功功率从48 MW 阶跃至96 MW，附录A 图A4 给出了其动态运行仿真波形。由图A4 可见，所提DCT及控制策略在动态阶跃过程中特性良好，DCT 高压侧直流电流响应时间约为5 ms，HMMC1、HMMC2及HMMC3 桥臂电流响应迅速。而在动态功率阶跃过程中，HMMC1、HMMC2 及HMMC3 桥臂pa、pb、na、nb 电容电压控制稳定且一致，表明所提控制策略在动态过程具有良好的均衡控制特性。

3.2.3 暂态运行仿真

为进一步验证所提DCT 拓扑及控制策略在暂态扰动下的控制性能，控制光伏系统向DCT 送入有功功率48 MW，并使得高压直流侧输入电压正极对地电压从200 kV 跌落为100 kV 以模拟直流变压器直流电源在输入侧的扰动。附录A 图A5 给出了其动态运行仿真波形。由图A5 可见，在暂态扰动过程中，HMMC1、HMMC2 及HMMC3 桥臂pa、pb、na、nb 电容电压控制稳定，且具有良好的均衡特性和控制响应速度。而在高压直流输入侧处于扰动期间，±20 kV 中压母线电压始终维持稳定，光伏系统有功功率送出同时保持稳定。综合上述仿真结果表明，所提拓扑及控制策略具有良好的稳定性和鲁棒性。

4 结语

面向未来大容量、高电压及能量双向传递要求下新能源全直流送出的工程前景，提出了基于MMC 的分相级联大容量高压直流变压器拓扑及控制策略。首先，介绍了该拓扑实现高、中压直流转换的机理及控制要求，并给出实现高、中压侧完全解耦的控制策略。高压侧设计5 个层次化电容电压控制架构实现3 个单相MMC 的完全稳定，并通过3 个单相V/f闭环控制建立中频交流电压。中压侧MMC采用电流双序控制，并在静止坐标系统下进行桥臂环流抑制以实现中压侧直流输出电压的稳定。而交流侧通过中频变压器实现高、中压侧电气隔离。最后，搭建电磁暂态仿真模型，通过稳态、动态及暂态仿真实验全面验证所提拓扑及控制策略的有效性。

本文所提的控制策略也可用于基于MMC 的柔性直流输电系统及其他直流变压器拓扑等应用场合。所提拓扑在故障条件下存在的过电压及抑制、保护配置等仍需进一步深入研究。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。