计及高比例风电暂态电压安全的主从协同动态无功优化方法

薛 霖，牛 涛，方斯顿，陈冠宏

（输配电装备及系统安全与新技术国家重点实验室（重庆大学），重庆市 400044）

0 引言

在“碳达峰·碳中和”背景下，以风电为代表的清洁能源在电力系统中的占比与日俱增。然而，大规模、高比例风电并网会导致并网节点附近网架结构薄弱、短路容量变小、无功电压支撑进一步短缺等问题。因此，近年来大规模风电场连锁脱网事故频繁发生，给风电的安全运行带来巨大挑战［1］。在传统水火电厂逐步减少、清洁可再生能源占比不断攀升的趋势下，维持合理的电压运行水平、预留充足的无功备用，对保证故障或扰动后系统能有足够的快速动态无功支撑尤为重要［2］。

针对含高比例风电系统的无功功率/电压预防控制和无功储备评估问题，目前已有学者进行了大量研究，主要包括本地集中式无功优化［3］、分布式无功电压控制［4］、多目标无功优化方法［5］等，对保障风电场的电压安全和稳定运行具有重大意义。文献［6-7］分别提出了故障前的大规模风电场无功电压预防控制策略和故障后的紧急控制策略。文献［8］提出了在不同的N-1 场景下，旨在最小化总发电量和安全控制成本的风电场电压预防控制方法。为精确计及风电出力的波动性，文献［9-11］提出基于模型预测控制方法，不断更新调整无功设备协调控制策略，保证系统安全运行。上述方法均为集中式优化策略，若要实现整个大系统的电压安全，需要同时保证主网和大规模风电场子站中每台机组的电压安全。通常，对于调度中心而言，难以直接获取风电场内部网络细节，也给集中式优化策略的在线实际应用带来巨大挑战［12］。

含高比例风电馈入的电力系统呈现典型的“主-从”特征，其电压安全相关的运行优化问题，可拆分成一个主问题和多个对应的独立子问题［13］。文献［14-15］提出了一种新的风电电压安全协调控制框架，实现对风电场的网损及节点电压的优化。为了避免过多的数据交互和保证风电场内部每台机组的电压安全，文献［16-17］提出了基于自治电压安全域的风电场无功功率/电压计算方法，虽然能充分考虑在设定场景下大规模风电系统每台机组的电压安全，但仅考虑故障前后的准稳态过程，无法精准刻画故障期间风电机组的电压暂态特性。文献［18］提出了一种两阶段鲁棒优化模型，对离散型和连续型无功补偿器进行协调，找到一种鲁棒最优解，但在风电渗透率过高、负荷过载等极端场景下，计算结果相对保守。此外，文献［19-20］针对风电机组电压波动大、连锁脱网等问题，提出了分层分级的无功功率控制策略。虽然该方法可以有效应对不确定性，避免保守决策，但当考虑大规模场站内所有机组的暂态特性时，还存在计算效率低的问题［21］。

计及所有N-1 场景和全部风电机组暂态特性的无功备用优化问题，本质上是特定形式的暂态安全约束最优潮流（transient security constrained optimal power flow，TSCOPF）问题，其计算规模异常庞大，上述已有文献中提出的无功备用优化方法，难以在计及暂态约束的同时实现大规模TSCOPF 问题的快速计算，无法直接用于高比例风电系统的无功储备优化在线评估及应用。为此，本文提出一种计及暂态约束的广义主从分裂（generalized masterslave splitting，GMSS）算法，实现主从系统的协同优化，计算出能够保证系统电压安全的无功备用裕度，同时保证计算的精度和收敛性。

1 计及暂态约束的高比例风电系统全局无功备用优化模型

通常，大规模风电通过升压变压器接入并网点（POC）母线，之后再集中汇入公共耦合点（PCC）母线接入主网。主网的集中控制器通过协调调度各个风电子站控制中心，形成主网系统和风电场子站的两级控制结构，如图1 所示。

图1 主网-风电两级结构示意图Fig.1 Schematic diagram of two-level structure of power grid and wind power

1.1 高比例风电系统全局无功备用优化模型

正常高比例风电系统的动态无功备用优化是计算出保证风电场运行和发生潜在N-1 扰动时，维持主网和各风电场子站母线电压都在安全裕度内，保障系统不诱发大规模连锁脱网的动态无功补偿设备需要预留的裕度。为保证无功备用评估的精度，需将风电系统和主网系统的暂态约束共同纳入最优潮流模型中，构建TSCOPF 模型。该模型的详细表述如下。

1）全局目标函数

本文选取主网中同步发电机和高比例风电系统中的静止无功补偿器（SVC）的无功出力作为控制变量，计算出调度周期内能够保证系统电压安全运行的最大动态无功备用裕度。

2）交流潮流等式约束

式中：Pg和Qg分别为同步发电机g注入的有功功率和无功功率；和分别为风电机组w发出的有功功率和无功功率；Qs为SVCs发出的无功功率；Pl和Ql分别为负荷l所消耗的有功功率和无功功率；Vi为节点i的电压幅值；Gij、Bij、θij分别为线路ij的电导、电纳和相角；B为系统节点集合。

3）不等式约束

不等式约束主要包括系统正常运行下各项变量运行限制。

4）暂态稳定约束

电力系统的暂态过程可以用以下微分-代数方程组描述。设整个系统在故障前处于稳态运行，式（4）表示稳态运行时的方程；在tbe时刻系统发生故障，tcl时刻故障切除，tf时刻系统暂态稳定仿真结束，则故障中和故障后系统微分代数方程分别由式（5）和式（6）描述。

在t=(0，tbe]阶段，有

在t∈(tbe，tcl]阶段，有

在t∈(tcl，tf]阶段，有

式中：x为系统的状态变量，包括发电机功角、直轴交轴暂态电势等；y为系统的代数变量，包括系统电压幅值、相角、线路传输功率等；u为系统的控制变量，包括主子站的无功控制设备；f0(·)、f1(·)、f2(·)、g0(·)、g1(·)、g2(·)为系统微分代数方程的紧凑形式，包括5 阶的双馈感应式风电机组、4 阶同步发电机、感应电机负载以及动态无功补偿装置的动力学方程［22］。式（4）—式（6）刻画出了系统在不同N-1 故障场景下的暂态特性。

由于风电场中风电机组在空间上呈辐射状分布，无功设备出力调节幅度在一定范围的前提下，本文采用轨迹灵敏度分析法将上述微分方程转化为代数方程。通过调整风电场出口母线上SVC 和系统同步发电机的无功变化，来记录各台风电机组母线终端电压曲线的变化，进而计算无功电压灵敏度系数，如式（7）所示。

为了保证在故障扰动情况下风电机组不脱网运行，风电机组机端暂态电压需要满足故障后的电压安全准则，如式（8）所示。

1.2 高比例风电系统无功备用优化问题的主从分解

随着风电渗透率逐渐升高，原始问题（式（1）—式（8））的规模也逐渐增大。若直接求解上述优化问题，集中式主站的存储和计算资源将面临巨大的求解压力，时间上也难以满足在线控制需求。因此，考虑将原始优化问题进行等价分解，实现主从协同求解，降低问题求解规模。为了推导方便，重新将上述全局无功备用优化模型写成如式（9）所示紧凑形式。

式中：下标M、B、S 分别表示主系统、边界系统、子系统；c(·)表示求最大动态无功备用裕度；u为控制变量，主要考虑的是同步发电机g和SVCs的无功出力Qg和Qs，u=[Qg，Qs]T；f(·)为系统的潮流约束；h(·)为系统的微分方程约束；g(·)为系统的不等式约束；λM、、wM、λB、、wB、λS、、wS为相应的等式约束和不等式约束的拉格朗日乘子。

主系统和子系统的耦合约束分别为边界系统的潮流等式约束fB(·)、微分方程约束hB(·)。首先，引入广义主从分裂算法将主从耦合项fB(·)进行拆分，得到主网和风电系统的潮流约束：

式中：fMB(·)、fBS(·)分别为主系统注入边界系统的功率和边界系统注入子系统的功率。

传统分解算法未考虑对含有微分方程约束的问题分裂，并且微分方程约束导致问题难以直接求解。因此，采用1.1 节中轨迹灵敏度方法将主系统、子系统、边界系统的微分方程转化为近似的代数方程，再对边界系统的代数方程进行拆分，即

式中：下标0 表示当前运行状态对应变量，下标1 表示在改变控制变量情形下的运行状态对应变量。不失一般性，可以认为主系统和子系统的控制变量主要对各自系统的状态变量有影响，且共同影响边界系统的状态变量。

2 主从分裂式无功备用优化模型

通过对边界系统的主从耦合约束条件分解，分别得到一个主网优化主问题和若干个风电场站优化子问题，下面给出详细模型。

2.1 主网侧主问题优化模型

主网侧的主问题，主要优化在主网中的运行约束和主网与边界系统的耦合约束下，同步发电机最大的无功备用容量。

1）目标函数

2）交流潮流等式约束

式中：Pi为节点i处有功功率；θi为节点i处相角；BM和BB分别为主系统和边界系统的节点合集。其中，式（13）和式（14）分别为主系统的潮流约束和主系统与边界系统耦合的潮流约束；式（14）中子系统的状态变量是通过自治求解子系统优化问题传递给主网侧优化模型的交互变量。

3）不等式约束

式中：LM为主系统的传输线路合集，包括电压幅值、线路传输功率、机组出力等约束。

4）电压暂态稳定约束

式中：Vz，t为发生第z个故障后t时刻的暂态电压；Vcur，t为当前状态的母线电压；和为发生第z个故障后t时刻的无功电压灵敏度系数；为子系统的控制变量，同样是通过自治求解子系统优化问题传递而来的交互变量。

2.2 风电场侧子问题优化模型

风电场侧子问题主要优化在子系统运行约束下，能够保证每台风电机组电压安全的SVC 最大无功备用容量。

1）目标函数

2）交流潮流等式约束

式中：BS为子系统的节点合集；子系统的状态变量是通过求解主系统优化模型传递给子系统优化模型的交互变量。

3）不等式约束

式中：LS为子系统的传输线路集合。

4）电压暂态稳定约束

3 主从优化模型的协同求解

3.1 边界一致性收敛判据

主网系统和各个风电子系统通过不断交替、更新边界系统的状态变量和相应的拉格朗日乘子变量实现主从系统协同优化计算，该算法的收敛性证明见附录B。为实现整个系统的无功备用评估，每个子工作站将各自风电场站的特定信息上传到主工作站，主工作站将协调所有风电场的运行状态，计算出边界耦合变量，并将信息发送回各自的风电场，具体见附录C 图C1。

在交替迭代过程中，如果主网系统和风电子系统n的边界参量在第k次和第k+1 次迭代的结果相差很小，则认为其满足边界一致性收敛条件。若主网系统和N个风电子系统都满足边界一致性收敛判据，则说明整个系统的协同求解完成。详细的边界一致性收敛判据见式（21）。

式中：下标n表示风电子系统n对应的变量；上标（k）表示第k次迭代对应的变量；xB=[VB，θB]T为边界系统的状态变量；λB=[]T和分别为边界系统的潮流方程和暂态电压方程的拉格朗日乘子；ε为收敛阈值。

3.2 主从协同求解算法

为了方便推导，给出主优化问题的紧凑形式见式（22）。

基于KKT 条件的异质分解，在给定边界系统初值的情况下，主问题式（22）和子问题式（23）分别为两个独立的非线性优化问题。可采用原对偶内点法分别交替求解主、子问题，基于边界信息一致性实现协同优化求解。本文是首先给定边界系统的初值从风电系统子问题开始计算，详细的主从协同优化求解流程如图2 所示。

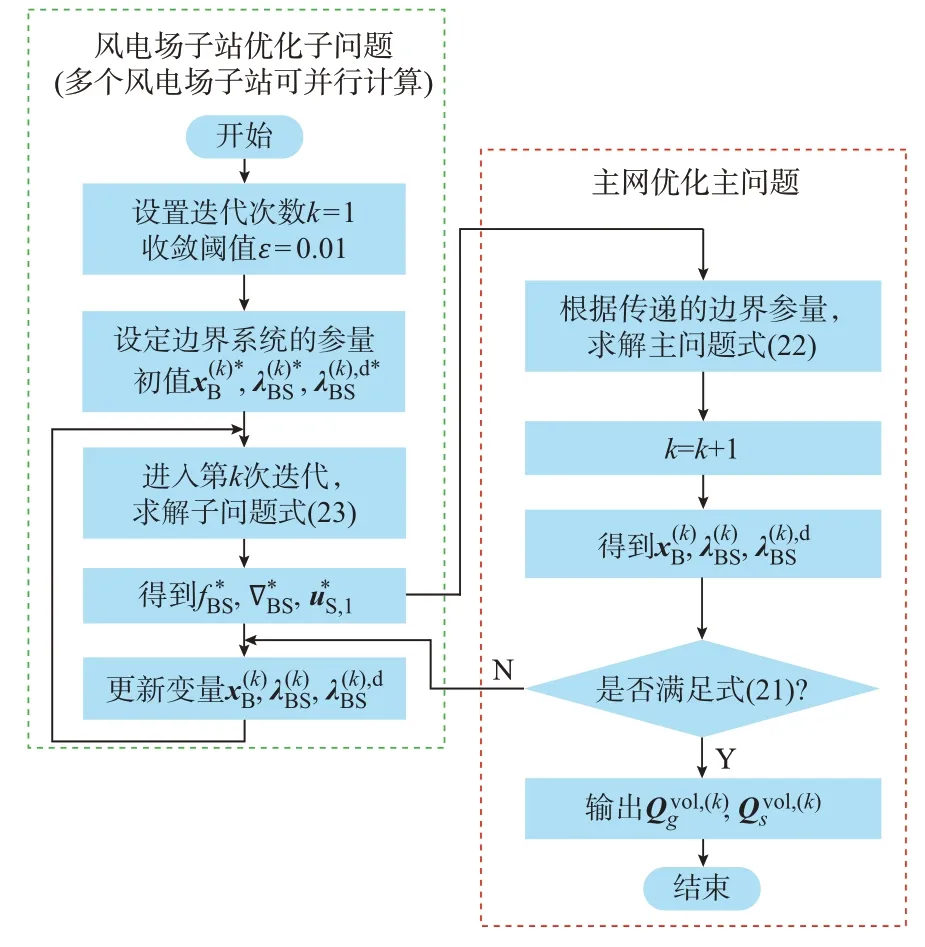
图2 主从协同优化算法的流程图Fig.2 Flow chart of master-slave cooperative optimization algorithm

4 算例分析

4.1 算例系统介绍

本节利用中国北部地区的某实际风电基地测试本文方法的精确性和时效性。此风电系统中包含5 个风电场，其接线示意图见附录C 图C2。5 个风电场QSY、WHP、DJH、GT 和LY 分别被记为风电场1、2、3、4、5。220 kV 的变电站（PCC）是5 个风电场的集中并网点，风电场通过汇集各条馈线再通过35 kV/110 kV 升压变压器并入110 kV 变电站（POC）。每个风电场出口处配备一定容量的SVC，在主网侧配备一定容量的同步发电机。由于本文中风电基地无功备用评估对应的时间尺度约为5 min，并未考虑有载调压器和电容电抗器等慢调节无功设备的动作。

本文利用PSAT 软件包进行电力系统时域仿真，无功备用优化模型通过MATLAB R2019a 编程实现，计算机所配置的处理器为Intel（R） Core（TM） i5-9500 CPU @ 3.00 GHz 以及8 GB 的RAM。由于本文的优化问题属于非线性优化，因此调用IPOPT 商业求解器进行求解。

4.2 算法性能对比分析

4.2.1 最优性分析

为验证本文方法的精确性，假设风电场1 出口处母线在1 s 时发生三相短路接地故障（0.1 s 后故障切除），系统的时域仿真总时长为6 s，仿真步长取0.01 s。基于时域仿真计算出的无功设备详细参数如附录C 表C1 所示。在此场景下，风电渗透水平为40%，针对TSCOPF 问题，分别采用集中式优化（下文简称TSCOPF-CO）和本文中计及暂态约束的广义主从分裂（下文简称TSCOPF-GMSS）算法分别进行系统的无功优化，记录下能够保证整个系统暂态电压安全的各个无功设备的无功备用容量裕度，如图3 所示。可以看到在精度上，利用两种算法计算出来的无功裕度基本一致，由于SVC 安装在风电出口母线侧，需要吸收风电机组发出的无功功率，所以是负值；而主网侧的同步发电机的无功裕度［0.12， 1.67］ p.u.为正值，是为了平衡主网负荷的无功消耗而发出无功功率。图3 中的绿色部分为能够保证系统电压安全运行的动态无功备用裕度。在计算精度上，本文的算法可以和集中式算法保持高度一致，证明了本文算法分解的最优性。

图3 TSCOPF-CO 和TSCOPF-GMSS 算法的精度对比Fig.3 Accuracy comparison of TSCOPF-CO and TSCOPF-GMSS algorithms

为了验证本文算法的有效性，对优化前后的风电场进行时域仿真验证，得到5 个风电场POC 母线的电压曲线，见附录C 图C3。图C3（a）表示在未进行无功优化时，POC1 的电压在故障情形下出现了振荡并且在故障后4 s 左右发生了越限。经过本文的无功优化后，将无功设备的出力控制在上述给定的无功裕度内，发现系统中所有POC 母线电压在故障后都处于电压安全范围内，如图C3（b）所示。证明了本文计算的无功备用裕度的有效性，能够保证整个系统的安全运行，避免连锁脱网事故的发生。

4.2.2 收敛性分析

为了验证本文算法的收敛性，在当前断面下，分别对比集中式优化算法和本文算法的计算时间，如附录C 表C2 所示。其中，利用本文算法求解时，子系统的求解时间取决于计算时间最长的风电子站（WHP），计算时间为4.646 7 s，总计算时间为主网侧计算时间加上计算时间最长的风电子站，为10.604 2 s，远小于集中式优化的37.632 1 s，表明在保证计算精度的前提下，大大提升了计算效率。

4.2.3 与其他算法的对比分析

为了进一步验证本文算法在不同场景下均能保持良好的最优性和收敛性，在风电场2、3、4、5 的出口处分别设置4 个N-1 故障场景，并与基于SCOPF 模型的文献［18］算法进行对比，得到不同算法在不同场景下的计算精度和计算时间。

附录C 图C4 为4 种典型故障场景下不同算法的计算精度对比。由于本文算法保证了分解前后的KKT 条件一致性，计算结果和原始集中式优化算法的结果一样。文献［18］提出了未计及风电机组暂态特性的电压预防控制策略并利用Benders 分解算法（下文简称SCOPF-Benders）求解，以避免大规模连锁脱网事故发生，因此，导致计算结果过于乐观。图C4（a）中，针对主网侧的同步发电机的无功裕度计算，SCOPF-Benders 计算得到的上边界和下边界的最大误差分别为55.06% 和25.64%；图C4（b）中，针对子站侧的SVC 的无功裕度计算，SCOPFBenders 计算得到的上边界和下边界的最大误差分别为15.99% 和9.93%。因此，SCOPF-Benders 未能较好地保证计算精度。

图4 分别展示了SCOPF-Benders 和TSCOPFGMSS 算法所计算的动态无功备用裕度的有效性。如图4（a）所示，以风电场1 为例，在SCOPF-Benders计算的动态无功备用裕度下，风电场1 内部的18 台风电机组（WT1 至WT18）在3.2 s 以后有明显电压越限现象，这是由于SCOPF-Benders 只关注N-1场景后的母线电压安全，未计及暂态过程的波动。如图4（b）所示，在TSCOPF-GMSS 计算的动态无功备用裕度下，风电场1 内部的18 台风电机组能够保证电压安全运行，避免连锁脱网事故的发生。因此，表明在高比例风电系统中考虑暂态约束对于风电场的电压安全运行至关重要。

图4 采用TSCOPF-GMSS 和SCOPF-Benders 时的风电场1 电压对比Fig.4 Voltage comparison of wind farm 1 by using TSCOPF-GMSS and SCOPF-Benders

附录C 表C3 展示了不同场景下本文算法与其他算法的计算时间。在4 种N-1 场景下，SCOPFBenders 的计算时间与本文算法TSCOPF-GMSS相似，平均计算时长均约为13.33 s，相较于原模型的平均计算时间44.31 s 有显著的减少。综上所述，本文算法在计算精度上能够保证和传统集中式优化的精度一致，在计算时间上与SCOPF-Benders 大致相同。因此，TSCOPF-GMSS 在分解优化过程能够兼顾计算时间和计算精度，在保证无功备用裕度计算精度的前提下，计算时间约为原始模型计算时间的30%。

4.3 实际大系统算例验证与分析

为进一步验证本文算法对实际大规模风电汇集区域的有效性，本节利用中国张北风电基地的万全风电汇集区域为测试系统。该系统的拓扑结构如附录C 图C5 所示。该大规模风电汇集区域电网具备20 kV 火电场1 000 MW、8 个风电场共计850 MW，包括的电压等级有35、110、220 kV，且汇集在同一并网点上集中外送，除PCC 汇集站和DJH 风电场POC 母线的电压等级是220 kV 外，其余风电场POC 母线的电压等级均为110 kV，其中，ZB 变电站为系统的并网点。该8 个风电场汇集场站的动态无功补偿设备参数见附录C 表C4。同样，在此系统中分别测试本文算法的精确性和收敛性，并与其他算法进行对比。

首先，为了验证本文算法能够被实际在线应用，在当前断面（风电渗透率为46%）下，记录了在7 个不同N-1 场景下不同算法对于实际风电汇集区域无功备用优化的计算时间，如附录C 表C5 所示。这里的故障场景考虑的是最为严重的三相短路接地故障。表C5 展示了不同故障场景下本文算法与其他算法的计算时间对比。虽然由于系统规模的增大导致本文算法TSCOPF-GMSS 的求解时间有所增加，但相较于传统的集中式优化TSCOPF-CO 的平均计算时间62.23 s，TSCOPF-GMSS 的平均计算时间为17.93 s，约为原始计算时间的28.81%，与未计及暂态约束的SCOPF-Benders 的计算时间相当，满足在线应用的要求。此外，可以看出系统规模越大，TSCOPF-GMSS 所提升的效率也越明显。这是由于TSCOPF-CO 需要计及大规模系统内所有节点，而TSCOPF-GMSS 对于风电子系统可以进行并行计算，子系统的求解时间取决于计算时间最长的风电子站，大大提升了计算效率。

图5 展示了在当前断面下不同算法所计算的动态无功备用裕度。相较于5 个风电场的小规模系统，该实际大规模风电汇集区域的平均动态无功备用裕度（图中的绿色区域）增大了25.23%。这是由于随着风电规模的增大，实际风电出力波动也相应增大，为了保证整个风电系统的电压都能够在安全域内，需要预留更多的动态无功备用裕度。从计算精度上来看，由于TSCOPF-GMSS 是基于KKT 条件一致性进行原始问题的分解，TSCOPF-GMSS 和TSCOPF-CO 所计算的动态无功备用裕度基本一致，保证了解的一致性。然而，由于SCOPF-Benders未计及风电的暂态电压特性，导致计算出的无功备用裕度偏大，最大误差达51.62%，未能较好地确保计算精度。

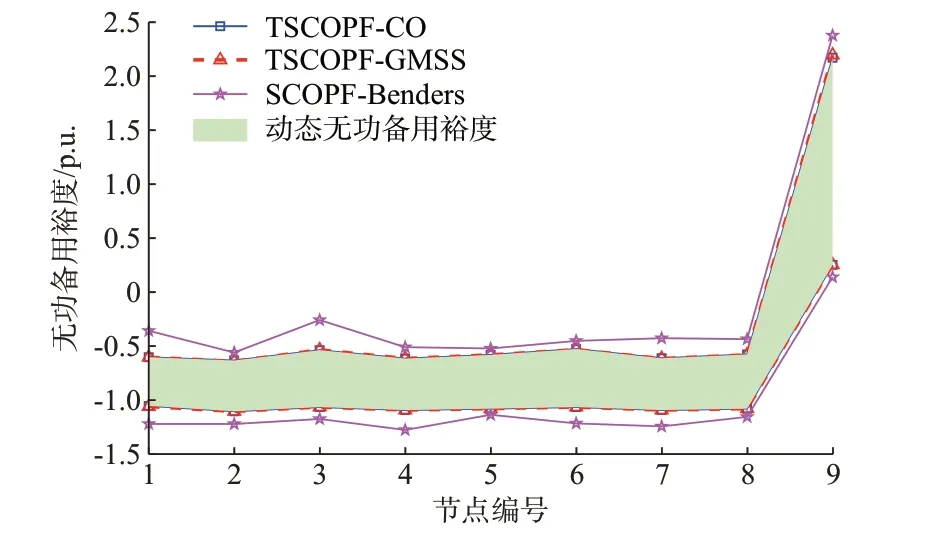
图5 不同算法的计算精度对比Fig.5 Comparison of computational accuracy of different algorithms

为了验证大规模风电汇集区域的动态无功备用裕度的可行性和有效性，附录C 图C6 给出了在当前动态无功备用裕度下，TSCOPF-GMSS 和SCOPFBenders 对于大规模风电汇集站的电压仿真验证对比。通过时域仿真可以得出，TSCOPF-GMSS 下风电机组暂态电压安全是可以保证的，可以避免连锁脱网事故的发生。然而，SCOPF-Benders 下的风力机组部分暂态电压超出了电压安全范围，如图C6（a）所示。例如，在SCOPF-Benders 下，风电场WF3 和WF6 电压在4.2～5.1 s 明显超出电压安全范围，并且风电场WF1 在故障过程中还出现了电压振荡，表明SCOPF-Benders 不能完全保证系统中所有风电机组的电压安全。

综上所述，经过实际大系统的验证，TSCOPFGMSS 和SCOPF-Benders 的总计算时间相似，约为原始模型计算时间的28.81%，说明TSCOPFGMSS 和SCOPF-Benders 都可以有效地缩短计算时间。但是，SCOPF-Benders 直接利用简化的稳态模型会导致最终的动态无功备用计算精度出现较大的偏差。此外，通过时域仿真验证，SCOPF-Benders无法完全保证风电机组的暂态电压安全性。因此，TSCOPF-GMSS 在保证计算精度的前提下，与原始的集中式优化算法相比，能够大幅度提升计算效率，并且能够保证系统中所有风电机组的暂态电压安全。

5 结语

本文针对高比例风电系统的电压安全问题，提出一种计及暂态约束的广义主从分裂优化算法。首先，与传统的集中式优化算法相比，基于KKT 条件推导分解后主、子问题优化模型，保证了计算精度。通过实际大规模风电系统仿真验证了其计算时间约为原始模型计算时间的28.81%，保证了在线应用。然后，与基于Benders 分解的风电汇集区域电压控制策略SCOPF-Benders 相比，由于本文计及了所有风电机组的暂态特性，所计算的无功裕度能够保证故障情形下的风电机组电压安全，并且计算时间和SCOPF-Benders 的计算时间基本相当。

未来，本文所提算法将扩展到含整数变量的优化问题，根据边界耦合方程推导分解后的模型形式，保证在含整数变量情况下计算的精确性和收敛性是需要研究的方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。