考虑小干扰同步稳定约束的电网新能源承载能力评估方法

2023-09-18孙荣富王小路邢纪奎

电力系统自动化 2023年17期

孙荣富，袁辉，王小路，丁然，邢纪奎

（1.国网冀北电力有限公司，北京市 100054；2.浙江大学电气工程学院，浙江省杭州市 310027）

0 引言

伴随中国“2030 年前实现碳达峰、2060 年前实现碳中和”战略目标的提出，大力发展以风电、光伏为代表的新能源已成为能源转型的必然选择［1］。在此背景下，中国电力系统将从以同步机为主导的传统电力系统逐渐演变为高比例新能源电力系统［2-3］。变流器作为新能源设备接入电网的主要接口，目前大多采用基于锁相环同步的跟网型控制方式（下文简称“跟网型变流器”）。然而，随着以跟网型变流器为接口的新能源数量和容量的增加，高比例新能源电力系统电网电压支撑强度（短路比）逐渐降低，容易引发锁相环主导的小干扰同步稳定问题［4-16］。例如：2015 年，中国新疆哈密风电基地出现了直驱风机与弱交流电网相互作用引发的振荡失稳问题，造成某电厂同步机脱网［2］；美国得克萨斯州因风电场引发的振荡事故，引发大规模风电机组脱网。小干扰同步稳定逐渐成为制约电网新能源承载能力的主要因素之一［17］。

目前，关于电网新能源承载能力评估已取得不少研究成果［18-20］。例如：文献［19］提出了一种基于非时序分析模型的新能源消纳能力量化评估方法，并分析了负荷、新能源装机容量、常规机组调峰率以及备用水平对新能源弃电率的影响；文献［20］在传统时序生产模拟模型的基础上，加入输电网潮流约束，提出了一种考虑输电网潮流约束的时序生产模拟模型，用于评估系统新能源年度消纳水平，所提模型考虑了线路容量约束和节点电压幅值约束对新能源消纳能力的影响。然而，文献［18-20］主要关注计及电力电量平衡和新能源出力随机性的灵活性规划以及计及电压越限的安全问题。

目前，仅有部分文献探讨了考虑小干扰同步稳定约束的电网新能源承载评估问题［21-23］。例如：文献［21］基于线性化系统状态空间模型，提出一种考虑特征值稳定约束的微网新能源机组出力优化方法；文献［22］针对多新能源场站并联接入电网场景，基于阻抗分析法提出了一种考虑小干扰同步稳定约束的电网新能源最大接入容量评估方法。大规模新能源并网场景下，系统具有设备数量多、动态模型维数高等特点，基于特征值稳定约束的电网新能源承载评估方法面临“维数灾”的问题；特征值计算需要已知系统的详细参数，而新能源设备由于厂商出于商业保密的目的，一般是“黑箱”模型，难以构造精确的系统线性化状态空间模型用于特征值计算；此外，文献［22］所提基于阻抗分析的电网新能源承载评估方法，假定新能源机组并联接入电网，难以考虑新能源场站空间分布及容量分配差异对稳定性的影响，适用场景受限。

为此，本文针对考虑小干扰同步稳定性约束的电网新能源承载能力评估问题，基于前期所提广义短路比理论，将小干扰同步稳定约束转化为广义短路比约束，构建电网新能源承载能力评估模型。进一步，将所构建的优化问题转化为具有网络结构保持和凸性质的半定规划问题，确保能够得到全局最优解，且可以考虑跟网型和构网型新能源设备并存的场景。最后，仿真验证了所提方法的有效性。

1 电网新能源承载能力评估问题描述

考虑图1 所示含n台新能源设备的多馈入系统，节点1，2，…，n为新能源设备馈入节点，节点n+1，n+2，…，n+m为中间无源节点，节点n+m+1 为外部等值电网节点，为简化分析，该外部等值节点近似为无穷大节点。其中，新能源设备采用常用的跟网型和构网型控制策略［24］。

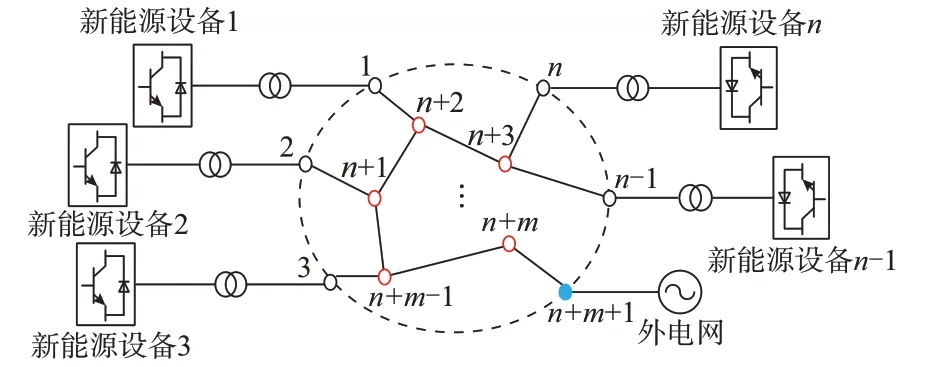
图1 新能源多馈入系统Fig.1 Multi-feed system with renewable energy

对于上述新能源多馈入电力系统，本文拟讨论的问题为：在网络参数、新能源设备控制参数和系统小干扰同步稳定裕度要求给定的情况下，如何评估电网新能源承载能力，即新能源最大可接入容量？

传统电力系统小干扰稳定约束相关优化问题，通常将系统主导特征根的阻尼比作为小干扰稳定量化指标。基于该传统分析思路，考虑小干扰同步稳定约束的电网新能源承载能力评估问题，具体可表示为：

式中：SBi为第i台新能源设备容量；ξ为小干扰同步稳定裕度；ξmin为给定的小干扰同步稳定裕度要求，这里设为3%。

然而，基于阻尼比约束的电网新能源承载能力评估问题（式（1））面临如下几个难题：1）阻尼比计算需要构建系统的状态空间模型，其前提是系统参数已知，然而新能源设备一般是“黑箱”模型，内部参数未知，难以构建精确的高比例新能源电力系统状态空间模型；2）新能源设备内部动态复杂，大规模新能源场景下，系统特征值计算将面临“维数灾”的问题，计算代价大。

为解决上述难题，将介绍一种新的新能源小干扰同步稳定裕度指标——广义短路比。

2 广义短路比理论回顾

针对图1 所示的新能源多馈入系统，给定如下假设条件：

假设1：交流网络连通且网络线路的阻抗比τ相同（τ=R/X，其中R、X分别为线路电阻和电抗）；

假设2：稳态时电力电子设备间母线相角差可近似忽略不计。

基于上述假设条件，适用于小干扰同步稳定性分析的多跟网型新能源并网系统闭环特征方程可表示为：

式中：Gi（s）为第i台新能源设备传递函数矩阵；γ（s）为网络线路动态传递函数矩阵，具体可参考文献［25］；SB为SBi组成的对角矩阵；Bred为仅保留新能源设备节点的网络节点压缩导纳阵；I2为单位矩阵；⊗表示Kronecker 积。

当新能源设备同构时，文献［16］指出，新能源多馈入系统闭环特征方程式（2）具有可解耦性质，这些解耦后单馈入系统的设备动态相同、短路比不同，其中，短路比最小的新能源单馈入系统代表了原新能源多馈入系统的稳定性。为此，文献［16］类比单馈入系统短路比的定义，将代表原新能源多馈入系统稳定性的解耦后新能源单馈入系统短路比定义为广义短路比。其中，该新能源单馈入系统闭环特征方程可表示为：

式中：G(s)为设备的传递函数矩阵；γgSCR为广义短路比，为拓展导纳矩阵S-1BBred的最小特征值。

当新能源设备异构时，文献［26］指出，利用模态摄动理论可构造近似代表原异构新能源多馈入系统稳定性的等效同构多馈入系统，进而原异构新能源多馈入系统稳定性可由该同构系统解耦后的最弱等效单机系统表示。其闭环特征方程表示为：

广义短路比的优势在于：将复杂的新能源多馈入系统小干扰同步稳定裕度量化问题转化为等效单机系统稳定裕度量化问题，其只需要通过求解等效单机系统的广义短路比和其临界值，即可避免对系统进行详细建模。值得一提的是，单新能源设备并网系统稳定性与电网强度呈正相关性，故不仅可以定义代表系统临界稳定的临界广义短路比。同时，可以定义代表任一给定稳定裕度下系统广义短路比数值γgSCR，ξ，具体描述如下：

式中：arg{·}表示求方程的根；sc=-σc+jωc为系统主导特征根，其中σc和ωc分别为实部和虚部，阻尼比为系统给定稳定裕度。特别地，当阻尼比ξc=0 时，式（6）得到的γgSCR，ξ为系统临界广义短路比。

观察式（6）可知，当新能源设备同构时，仅需根据单机系统即可求得γgSCR，ξ；当新能源设备异构时，等效单机系统包含各个异构设备的动态，相比于新能源设备同构情况，γgSCR，ξ的计算难度增加。参考文献［26］可知，等效单机系统的稳定性常介于异构系统中不同设备单机并网系统的稳定性之间。换句话说，如果已知异构系统中不同设备单机并网系统对应的短路比γgSCR，ξi，那么等效单机系统的γgSCR，ξ介于γgSCR，ξi之间。

此外，由文献［24］可知，对于锁相环主导的小干扰同步稳定问题，构网型新能源设备接入电网时，可看成接入节点增加一条等效电纳为SBVSMBp的对地支路（Bp为单位容量新能源设备的等效电纳，SBVSM为新能源设备容量），即构网型新能源设备接入电网主要影响系统的广义短路比而不影响系统的临界广义短路比。

3 电网新能源承载能力评估方法

第2 章指出，广义短路比可用于评估新能源多馈入系统小干扰同步稳定裕度。为此，将广义短路比替换式（1）中的阻尼比约束，电网新能源承载能力评估模型可表示为：

目前，实际电网中主要以锁相环同步的跟网型新能源设备为主。然而，典型跟网型新能源设备缺乏对电网的电压支撑，高比例新能源电力系统背景下振荡问题突出。已有研究表明，构网型变流器接入电网能有效提升系统的电压支撑强度［24］，在实际电网配置构网型新能源设备逐渐受到重视，未来电网可能呈现跟网型/构网型新能源设备混联的趋势［27］。考虑到跟网型新能源设备和构网型新能源设备结构的差异性，下面将分两种场景讨论计及考虑小干扰同步稳定约束的电网新能源承载能力评估问题。

1）场景1——多跟网型新能源设备并网系统

此时，优化问题式（7）可进一步表示为：

考虑到实际情况，新能源设备容量SBi需要大于等于0。

优化问题式（8）中，考虑到求解过程中新能源设备的容量可能会为0，此时对角矩阵SB为半正定矩阵且不可逆，故难以直接通过S-1BBred求解γgSCR，ξ。由于Bred为正定矩阵，故S-1BBred的最小特征值为SBZred（Zred为Bred的逆）最大特征值的倒数。在此基础上，可将优化问题式（8）转化为：

式中：λmax为求解矩阵的最大特征值。

优化模型式（9）的好处在于能够考虑新能源设备容量为0 的情况。此外，考虑到异构时γgSCR，ξ的求取涉及各异构设备动态（参考式（6）），计算较为困难，参考上文分析，取γgSCR，ξ的上界γUgSCR，ξ，将优化问题式（9）表示为：

步骤1：构造原新能源多馈入系统中各个跟网型新能源设备对应的单机并网系统。当新能源设备为“黑箱”模型时，基于物理实验平台或数字仿真平台，搭建各个新能源设备对应的单机并网系统；当新能源设备为“白箱”模型时，可直接构造每个新能源设备对应单机并网系统的闭环特征方程。

步骤2：计算给定稳定裕度阈值下，各个跟网型新能源设备单机并网系统对应的短路比，即计算γgSCR，ξi（i=1，2，…，n）。当新能源设备为“黑箱”模型时，可采用实验法的思路，对各个单机系统注入一个小扰动，记录新能源设备的时域仿真波形，根据波形的峰值和峰值间的时间间隔信息，可评估对应短路比下系统主导特征值的阻尼比信息。如果阻尼比达到给定阈值，则对应的短路比为该单机系统在给定稳定裕度下对应短路比，即γgSCR，ξi；如果阻尼比未达到给定阈值，则改变短路比数值；重复上述实验，直到获取该单机系统给定稳定裕度阈值下对应的γgSCR，ξi。当新能源设备为“白箱”模型时，可采用解析法的思路，通过求解单机系统的闭环特征方程，得到不同短路比下系统主导特征值的阻尼比，进而获取给定稳定裕度阈值下各个新能源设备单机并网系统对应的短路比γgSCR，ξi。

步骤3：取γgSCR，ξi(i=1，2，…，n)的最大值，即原新能源多馈入系统给定稳定裕度下广义短路比的上界。

需要注意的是，实际中可以根据新能源设备的厂商和型号信息，将各新能源设备进行分类，对于同一厂商和型号的同构设备，只需计算一台新能源设备的γgSCR，ξ，即可减少求解的计算代价。

值得一提的是，相较于传统基于阻尼比约束的优化问题式（1），优化问题式（9）避免了系统动态模型的详细建模，大大简化了优化问题式（1）的求解难度，适用于大规模新能源并网场景。此外，适用于新能源设备参数未知场景（可采用实验法求得）。

然而，优化问题式（10）涉及特征值约束，是个非光滑、非线性优化问题，直接对其求解很难保证找到优化问题的全局最优解。由矩阵不等式性质可知，可将优化问题式（10）中的特征值不等式约束等价变化为如下形式：

式中：I为单位矩阵。

此外，由于优化问题式（10）中的最大特征值λmax(SBZred)等价于（Z为网络结构保持的网络阻抗矩阵），矩阵不等式（11）可进一步表示为：

式中：B为结构保持的网络导纳矩阵，B=Z-1。

将式（12）代入式（10），可将优化问题式（10）等价转化为如下考虑网络结构保持的半定规划问题：

值得一提的是，对于实际中给定的连通网络，新能源的总容量总是有界的，且总能找到充分小的新能源容量分配使系统广义短路比大于，这说明半定规划问题式（13）存在下界且存在严格可行解。结合文献［28］可知，具有凸性质的半定规划问题式（13）总是存在全局最优解，该问题可通过内点法高效求解。还需值得注意的是，优化模型式（13）保留了网络结构信息，可用于指导分析考虑无源节点辅助设备接入的相关优化问题，同时由于保留了网络导纳矩阵的稀疏性，可提升原优化问题的求解效率。

2）场景2——电网中允许接入一定容量的构网型新能源设备

此时，优化问题式（7）可表示为：

式中：SBSVMi为第i台构网型新能源设备的容量。考虑到构网型新能源设备仍处于实验阶段，未来相当长一段时间电网配置的构网型新能源可能有限，为此给定S0代表允许接入的构网型新能源设备最大总容量；γgSCR为拓展导纳矩阵S-1BB′red的最小特征值，其中，B′red为考虑构网型新能源设备接入后电网的等效导纳矩阵，具体如式（15）所示。

式中：SBSVM为SBSVMi组成的对角矩阵；Bp为Bpi组成的对角矩阵，其中，Bpi为第i台构网型新能源设备的单位容量下的等效导纳。

为便于优化问题式（14）的求解，用γgSCR，ξ的上界替换优化问题式（14）里不等式约束中的γgSCR，ξ，并且结合式（11）、式（12）和式（15），可将优化问题式（14）中的第1 个不等式表示为：

将式（16）代入式（14），可将优化问题式（14）转换为如下半定规划问题：

当跟网型新能源设备同构时，优化问题式（17）与原优化问题式（14）等价，即优化问题式（17）的最优解为原优化问题式（14）的全局最优解；当跟网型新能源设备异构时，优化问题式（17）相较于原优化问题式（14）较为保守，故优化问题式（17）的最优解可理解为原优化问题式（14）的次优解。

综上所述，本文所提基于广义短路比的电网新能源承载能力评估方法流程如图2 所示。具体流程总结如下：

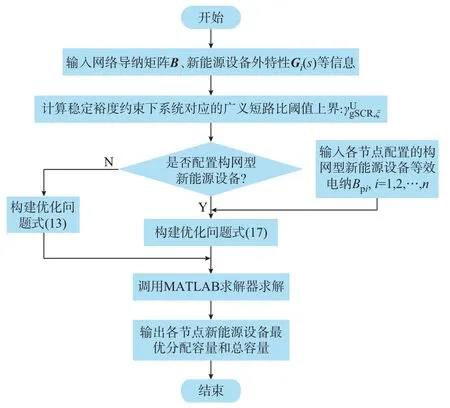
图2 考虑小干扰同步稳定约束的电网新能源承载能力评估流程图Fig.2 Flow chart of assessment for accommodable renewable energy capacity of grid considering small-signal synchronous stability constraints

首先，求解网络节点导纳矩阵B，并获得给定的新能源设备外特性Gi（s）信息以及能够配置新能源设备的节点信息。

其次，计算给定小干扰同步稳定裕度约束下原新能源多馈入系统广义短路比上界，可采用实验法或解析法获得，具体计算流程参考上文介绍。

然后，根据是否接入构网型新能源设备两种场景，构造相应的电网新能源承载能力评估模型。具体地，当不考虑构网型新能源设备接入时，构造优化问题式（13）；当考虑构网型新能源设备接入时，结合各个节点配置的构网型新能源设备等效电纳信息Bpi（i=1，2，…，n），构造优化问题式（17）。

最后，针对不同场景下所构造的半定规划问题，调用MATLAB 求解器进行求解，输出计算得到的各节点新能源设备最优分配容量和总容量信息。

4 算例分析

为验证所提电网新能源承载能力评估方法的有效性，在MATLAB/Simulink 环境下搭建如图3 所示39 节点系统。图3 中：新能源设备控制参数见附录A 表A1，网络参数参考文献［29］；节点1～12 为可以放置新能源设备的节点，其中，新能源设备可代表风电场。下文算例分析中考虑3 种情况：1）仅考虑接入跟网型新能源设备且设备同构；2）仅考虑接入跟网型新能源设备且设备异构；3）在情况2 的基础上，允许加入构网型新能源设备。

图3 12 机39 节点系统Fig.3 12-machine 39-bus system

4.1 情况1：仅接入跟网型新能源设备且设备同构

各新能源设备都采用恒直流电压控制模式。通过单新能源设备并网系统实验可得，当阻尼比为0.03 时，γgSCR，ξ=3.1。采用YALMIP 求解器求解，迭代过程中半定规划问题式（13）的对偶间隙变化如图4 黑色虚线所示（黑色虚线与蓝色实线代表的对偶间隙轨迹近似相同，黑色虚线被蓝色实线覆盖）。由图4 可知，迭代到第12 次时，对偶间隙小于10-6，近似为0。这说明情况1 下半定规划问题式（13）找到了全局最优解。求得的半定规划问题式（13）最优解见附录A 表A2，电网最大可承载新能源容量为

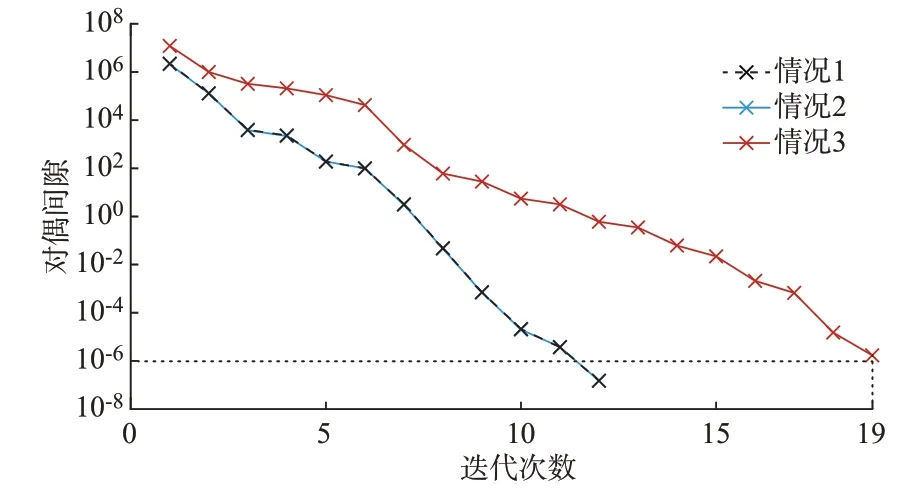
图4 情况1～3 下所提评估模型迭代求解过程的对偶间隙Fig.4 Dual gap of iterative solution process for proposed assessment models in scenarios 1～3

此外，以等容量分配方法为对比案例。令各新能源设备容量相等且等比例增加，计算系统相应主导特征值的阻尼比，直到系统稳定裕度达到阈值。计算得到等容量分配方法下电网允许接入的新能源设备最大总容量为10.02 p.u.（此时各新能源设备容量为0.835 p.u.）。对比可知，本文所提方法可提升26.1%的电网新能源承载能力，这说明相比于等容量分配方法，本文所提方法能有效提升电网新能源承载能力。

进一步地，结合时域仿真分析验证所提电网新能源承载能力评估方法的有效性。将12.64 p.u.平均分配给各新能源设备（SBi=1.053 p.u.）。在附录A 表A2 所示容量分配方法（方法1）和各新能源设备容量为1.053 p.u 的分配方法（方法2）下，各新能源设备有功功率时域波形如图5 所示。图中：t=1 s时，节点39 电压跌落0.05 p.u.，0.05 s 后故障恢复。由图5 可以看出，如果将半定规划问题式（13）求得的承载总容量平均分配给各新能源设备，系统由稳定变为不稳定。因此，与等容量分配方法相比，本文所提电网新能源承载能力评估方法更优，仿真结果说明了所提方法的有效性。

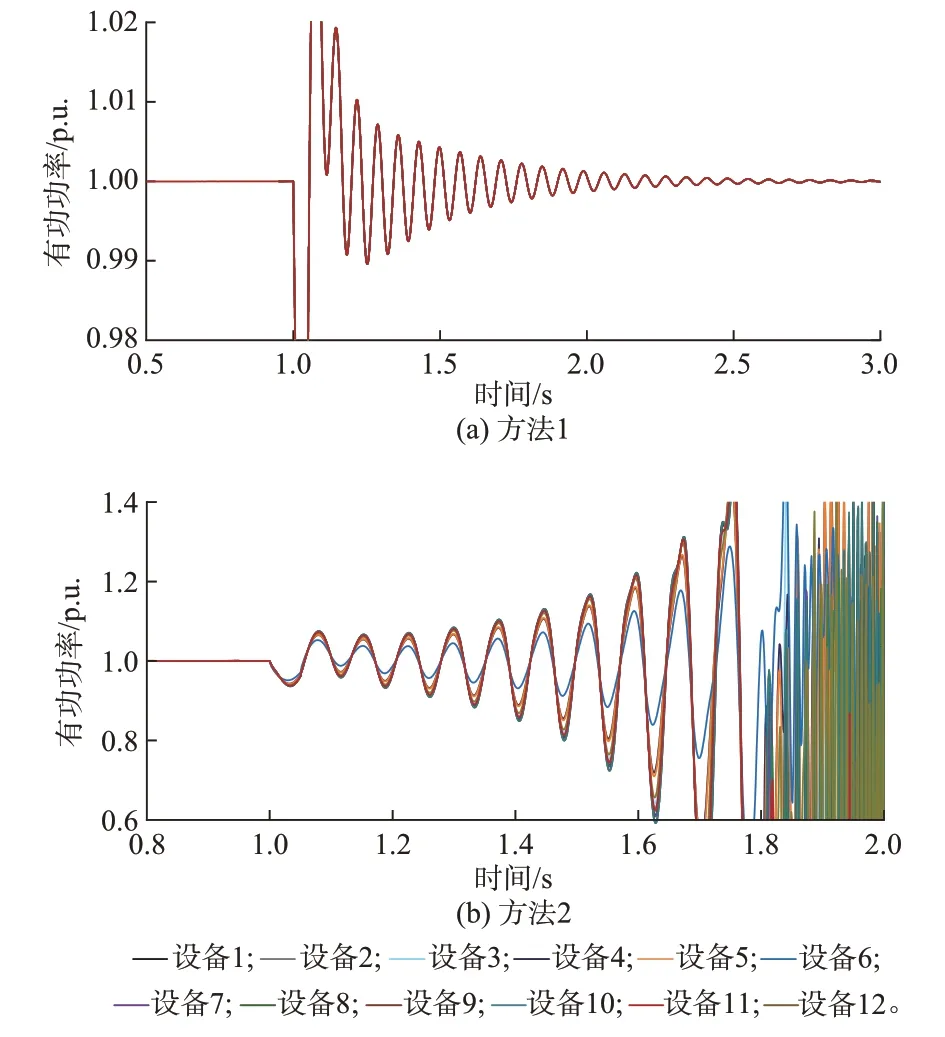
图5 不同容量分配方法下的时域波形（情况1）Fig.5 Time-domain waveforms with different capacity allocation methods （case 1）

4.2 情况2：仅接入跟网型新能源设备且设备异构

为构造异构新能源多馈入系统算例，考虑新能源设备1～4 采用恒有功功率外环，其余新能源设备采用直流电压外环；设备1～4 的锁相环的比例、积分参数设为23 和7 800，设备9～12 锁相环的比例、积分参数设为25 和7 200。

首先，说明异构新能源多馈入系统稳定性常介于异构系统中不同新能源设备对应的单机并网系统稳定性之间。考虑如下不同情况：令新能源设备5～12 容量为1 p.u.，新能源设备1～4 的容量由1 p.u.减小到0.1 p.u.，此时系统对应的γgSCR由2.6 增加到3.77。附录A 图A1 给出了这些情况下原新能源多馈入系统主导特征值的阻尼比曲线。此外，还给出了当γgSCR由2.6 变化到3.77 时，原新能源多馈入系统中不同设备构成的单机并网系统里稳定性最弱单机系统和最强单机系统阻尼比变化曲线。由附录A图A1 可以看出，随着γgSCR的变化，原新能源多馈入系统稳定性介于原系统中不同新能源设备对应的最弱单机并网系统和最强单机并网系统的稳定性之间。

其次，说明所提电网新能源承载能力评估方法适用于异构场景。由附录A 图A1 可以看出，阻尼比为0.03 时，系统为3.3。将其代入半定规划问题式（13）并利用YALMIP 求解器求解。求解迭代过程中，优化问题的对偶间隙变化如图4 蓝色实线所示。由图4 可知，迭代到第12 次时对偶间隙近似为0，说明情况2 下优化问题式（13）找到了全局最优解。各节点新能源设备容量最优分配见附录A表A3，电网可接入新能源最大总容量为=11.87 p.u.。此外，以等容量分配方法作为对比，求得该方法下电网可接入的新能源设备最大总容量为9.78 p.u.（各节点新能源设备容量为0.815 p.u.）。与等容量分配方法相比，采用本文所提方法，新能源承载能力提升了21.4%，故本文所提方法更优。

需要说明的是，当新能源设备控制参数变化时，其主要通过影响系统的γgSCR，ξ和进而影响电网新能源的承载能力。当新能源设备控制参数变差时，给定稳定裕度下，系统对应的电网强度γgSCR，ξ增大，电网可接入的新能源设备总容量减小。如果γgSCR，ξ的上界也增大，那么基于所构造的半定规划模型，求解得到的新能源设备接入最大总容量也变小。反之，如果新能源设备控制参数改善时，给定稳定裕度下，电网可接入的新能源设备总容量增大。例如：将新能源设备1～4 锁相环的比例、积分参数设为22 和7 900，计算得到为3.5，代入优化问题式（13），求解得到电网能接入的新能源设备最大总容量为11.192 p.u.。对比上述为3.3 对应的最大接入容量11.87 p.u.可知，当增大时，电网能接入的新能源设备最大总容量减小。

进一步地，结合时域仿真分析验证所提电网新能源承载能力评估方法的有效性。在附录A 表A3所示容量分配方法（方法3）和各新能源设备容量都为0.989 p.u.、总容量为11.87 p.u.分配方法（方法4）下，各新能源设备有功功率时域波形如图6 所示。其中，t=1 s 时，节点39 电压跌落0.05 p.u.，0.05 s 后故障恢复。由图6 可知，将半定规划问题式（13）求得的电网可接入的新能源设备最大总容量平均分配给各新能源设备时，系统由稳定变为不稳定。故相较于等容量分配法，本文所提电网新能源承载能力评估方法更优。

图6 不同容量分配方法下的时域波形图（情况2）Fig.6 Time-domain waveforms with different capacity allocations （case 2）

4.3 情况3：考虑构网型新能源设备接入且跟网型设备间异构

在情况2 的基础上，为便于分析，假设单位容量下各构网型新能源设备外特性等效电纳为1.3 p.u.，且图3 中39 节点系统可接入的构网型新能源设备容量为1 p.u.。在此基础上，利用YALMIP 求解器求解优化问题式（17），求解迭代过程中，对偶间隙变化如图4 红色实线所示。由图4 可知，迭代到第19 次时对偶间隙约为10-6，近似为0。这说明优化问题式（17）找到了全局最优解。求得的各节点跟网型和构网型新能源设备容量最优分配结果如附录A 表A4 所示，总容量为13.237 p.u.。与情况2 求得的电网可接入新能源设备的最大总容量（11.87 p.u.）对比可以发现，构网型新能源设备接入有利于提升小干扰同步稳定约束下电网新能源承载能力。

此外，为说明本文所提方法的有效性，这里选取以下4 种场景作为对比案例，计算相应的电网新能源设备最大可接入总容量：

场景1：构网型新能源设备全部装在节点1，等容量增加节点1～12 接入的跟网型新能源设备容量，直到系统阻尼比达到0.03；

场景2：构网型新能源设备全部装在节点5，等容量增加节点1～12 接入的跟网型新能源设备容量，直到系统阻尼比达到0.03；

场景3：构网型新能源设备全部装在节点10，等容量增加节点1～12 接入的跟网型新能源设备容量，直到系统阻尼比达到0.03；

场景4：构网型新能源设备等容量分配在节点1～12，等容量增加节点1～12 接入的跟网型新能源设备容量，直到系统阻尼比达到0.03。

计算可得，上述4 种场景下电网新能源可接入最大容量分别为10.26、10.116、10.32、10.224 p.u.。此外，本文所提方法计算得到的电网新能源最大接入容量为13.237 p.u.。可以看出，相比于上述4 种场景的新能源配置方法，本文所提方法至少能提升28.3%的新能源设备可接入容量，说明了本文所提方法能有效增加小干扰同步稳定约束下电网的新能源承载能力。