RRPRR型五杆机构开式轨迹综合研究
2023-09-18辛军炜邓援超宋志成蔡宇飞
辛军炜, 邓援超, 宋志成, 蔡宇飞
(湖北工业大学 机械工程学院,武汉 430068,E-mail:yiyuansdiy@163.com)
平面五杆机构是杆数最少的二自由度机构[1],由于运动副都为低副,其承载能力大,因此在工程上应用广泛。相对于四杆机构,五杆机构具有较高的柔性,其中RRPRR型五杆机构的可动性不受杆长条件的约束[2],末端工作点具有较高的柔性,可实现较复杂的运动轨迹。
在连杆轨迹生成的研究中,由于傅里叶描述符对轨迹有很好的描述,且轨迹曲线的平移、缩放、旋转对曲线的特征参数没有影响,通过曲线特征参数拟合的方法得到了广泛应用。主流的方法有通过数值图谱法将曲线的特征参数存储在计算机中后使用模糊识别算法进行匹配,以及采用拟合算法通过曲线的特征参数进行连杆参数拟合。褚金奎等[3]通过谐波特征参数法,对连杆机构的尺寸,机构安装位置,连杆上工作点的位置参数进行综合,建立了数值图谱库;冯立艳等[4]通过建立机构实际尺寸和安装参数与傅里叶特征谐波参数之间的关系,结合遗传算法对五杆机构的特征尺寸进行优化拟合;李学刚等[5]通过将五杆机构进行拆分,提出采用傅里叶级数法对平面五杆机构轨迹代数求解的方法;丁健生等[6]基于最小二乘法,利用傅里叶级数对位置点近似逼近,实现了少位置离散点特征提取的方法;Uesaka等[7]提出了一种将曲线总曲率的复指数函数通过扩展的傅里叶系数展开,从而得到的新的傅里叶描述符,使之适用于开式曲线和闭式曲线的拟合。Yue等[8]构建了由常用平面连杆机构生成的开、闭平面曲线库,从而将连杆曲线生成问题转化为库搜索问题和局部优化问题。
目前采用傅里叶级数法的连杆轨迹曲线综合中,由于傅里叶级数的性质,多是针对整周采样点进行的连杆曲线拟合。工程实际中,往往只给出了部分轨迹的采样点,如在包装机械中,往往只需要机构满足一部分轨迹曲线,对整周的轨迹并没有要求,针对这一问题,研究借鉴了傅里叶描述符的特点,通过与最小二乘法结合,借助遗传算法,对开式曲线进行拟合。
1 开式曲线的傅里叶描述符
在傅里叶级数理论中,任何周期函数都可以由正弦函数以及余弦函数组成的无穷级数表示。通过在复平面中建立坐标系,用傅里叶级数的复数形式表示由连杆运动轨迹曲线所形成的复函数,且此过程可逆。
本篇论文的开式曲线的傅里叶描述符采用最小二乘法,通过定义傅里叶描述符对任务轨迹曲线进行拟合,当只给出了部分的连杆运动轨迹时,首先建立该连杆机构任务点的傅里叶级数的复数方程,之后将经拟合后的傅里叶系数与复数方程的系数进行匹配,根据复数方程中杆件的相互关系得出连杆机构的各个参数。
对于平面连杆机构的运动轨迹可以看做一个复函数在复平面上形成的曲线,当连杆曲柄转动一周时,工作点所形成的曲线可以看做周期函数的采样,这些采样点可表示为复数形式z(t)=x(t)+jy(t),一个等时间间隔采样的点数为N的离散傅里叶逆变换(IDFT)可表示为
(1)
此时z为原函数,An为傅里叶系数,其中n=0,1,…,N-1。则傅里叶系数An可表示为
(2)
以上公式为封闭曲线的傅里叶展开式。在开式曲线中,由于其采样点未包含整周采样点信息,我们无法直接使用傅里叶变换。在此,我们使用最小二乘法去近似拟合曲线的傅里叶系数,称之为开式傅里叶描述符。它们的形式为
(3)
其中:p为谐波成分的阶数,且k∈[-p,p];系数αk为傅里叶描述符的系数,代表每个圆周运动的半径(为|αk|)和初始相位(为∠αk)的复矢量,通过首尾相接,分别以角速度kω0运动从而得到z(t)[9],这些旋转矢量又叫做谐波分量。
根据离散傅里叶级数理论,低阶谐波成分用来描述曲线的轮廓,高阶谐波成分用于描述曲线细节。故阶数越高,傅里叶表达式的项数越多,对曲线的描述也就越精确。当谐波成分为3阶时,对曲线轨迹点的拟合误差已经小于1%(下文有例证),可以满足实际需求,若需要进一步提高拟合的精度,则可以通过提高拟合的阶数[10]。
最小二乘法又称最小平方法,通过最小化平方误差得到与目标数据点匹配的最佳函数匹配,常用于曲线拟合。采用构建误差函数进行最小二乘法拟合来求解系数αk,通过最小化Δ值,从而得到最佳的系数值αk
(4)
式(4)中的z(t)为原始曲线,可将其转为复数矩阵形式求解
GX=Y
(5)
对式(5)使用LU分解进行运算[11]
(6)
其中:θi=ω0ti;k,m∈[-p,p];且p为谐波成分的阶数。至此,经过解矩阵方程,我们可以得到矩阵X,矩阵X中各个αm即为轨迹曲线各阶次的傅里叶系数αk,进而得到拟合曲线的函数表达式z(t)。
2 RRPRR型五杆机构连杆曲线分析
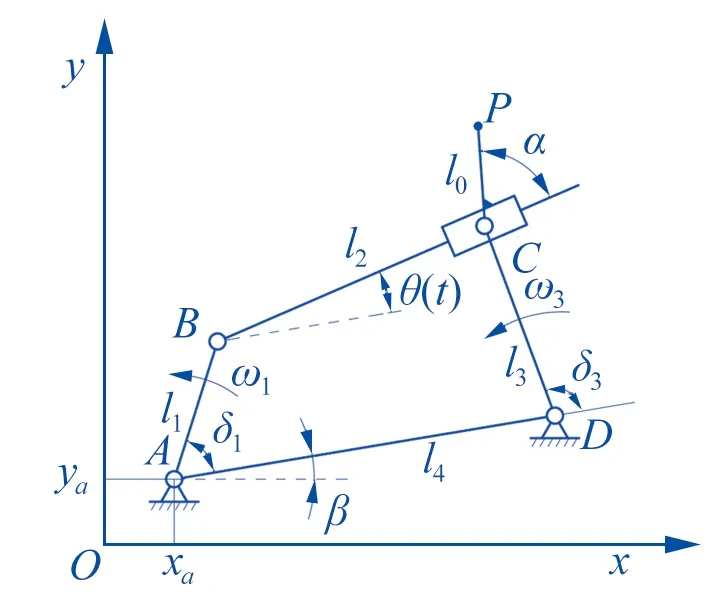
▲图1 一般位置下滑块五杆机构运动简图
如图1所示,该RRPRR型五杆机构有两个自由度,以曲柄AB与曲柄DC为主动件,转动角速度分别为ω1和ω3,与机架AD的初始转角分别为δ1和δ3,并设δ1和δ3的初始的相位差为δh,其中角β为机架AD与x轴之间的夹角,角θ为连杆BC与机架AD间的夹角,并随着连杆机构运动的时间而变化。A点坐标为(xa,ya),BC间的距离l2随滑块C的运动而变化,滑块C上固连展杆CP的长度为l0,展杆CP与杆BC之间的夹角为α,当曲柄AB和曲柄CD转动时,工作点P运动所行成的轨迹即为五杆机构的轨迹曲线。
如图1,设曲柄AB与曲柄DC转动的角速度比ω1∶ω3=h∶v,且h和v均为任意整数。δ1和δ3的关系为
δ1=δh+δ3
(7)

(8)
通过ABCDA形成的闭环,得到对应的矢量方程为
(9)
式(9)的复数形式为
(10)
将式(10)取共轭后得到
(11)
将式(9)和式(10)相除消l2后,即可得到以连杆摆动角θ(t)为变量的转角函数ejθ(t):
(12)
式中:“±”号表示同一机构的两种构型,取“+”号表示该机构为正装机构,“-”号表示该机构为反装机构。本篇论文采用正装机构,式(12)的转角函数取正号。
在RRPRR型双自由度五杆机构中,影响机构工作点P轨迹曲线的因素有:两原动件角速度比ω1∶ω3以及10个位置参数l1、l3、l4、l0、α、xa、ya、β、δ1、δ3[12]。其中l1、l3、l4为基础尺寸,l2为关联尺寸与l1、l3、l4的取值有关,在保证杆长l2满足连杆持续运动条件下,l2的取值不影响连杆机构运动轨迹。当基础尺寸给定时,展杆参数l0和α决定工作点P的运动轨迹的形状和大小,xa、ya和β决定连杆轨迹的位置和方向,δ1的取值与δ3和δh有关,且其中δ1和δ3决定了工作点P的初始位置。
当曲柄AB和曲柄DC转动方向相同时,满足该五杆机构能够连续转动的杆长条件为[13]
(13)
当连杆机构整周转动时,转角函数ejθ(t)的傅里叶变换为

(14)
式(14)中:ck为第k次谐波分量的幅值;φk为第k次谐波分量的初相位;θ(t)是连杆BC相对于机架AD的摆角θ的函数。
当给出的拟合点少于一个周期,即为一个开式曲线时,转角函数ejθ(t)则不是一个周期函数,不能采用傅里叶变化得到系数ckejφk的值,但可通过第一节中最小二乘法拟合的方法获得。
3 平面五杆机构的谐波特征参数
如图2(a)所示,滑块五杆机构在标准位置下,A点位于坐标原点O点,机架AD与x轴重合,且曲柄DC与机架AD共线,此时曲柄AB与机架AD的初始夹角为δh。曲柄AB与曲柄DC转动的角速度比ω1∶ω3=h∶v,且h和v均为任意整数。

▲图2 两种位置下滑块五杆机构运动简图
代入转角函数ejθ(t)的傅里叶级数表达式后,此时工作点P点的轨迹曲线则通过傅里叶描述符的形式表达,具体为
rP(t)=rAD+rDC(t)+rCP(t)=l4+l3ejvωt+
l0ejα(c0ejφ0+c1ejφ1ejωt+c-1ejφ-1e-jωt+c2ejφ2ej2ωt+
c-2ejφ-2e-j2ωt+…+ckejφkejkωt)
(15)
当曲柄DC以恒定角速度vω转动δ3的角位移时,P点的傅里叶级数展开式为
rP(t)′=l4+l3ejδ3ejvωt+l0ej[α+θ(t+δ3/v)]=
l4+l3ejδ3ejvωt+l0ejα[c0ejφ0+c1ej(φ1+δ3/v)ejωt+
c-1ej(φ-1-δ3/v)e-jωt+c2ej(φ2+2δ3/v)ej2ωt+
c-2ej(φ-2-2δ3/v)e-j2ωt+…+ckej(φk+kδ3/v)ejkωt]
(16)
如图2(b)所示,一般位置下五杆机构的配置中:A点相对于原点O有R的位置偏移以及μ的角偏移,其坐标的向量表示为Rejμ,且机架AD相对于x轴有β的角度;当曲柄DC相对于机架AD以恒定角速度vω转动δ3的角位移时,曲柄AB以hω的角速度转动,并相对于机架AD有δ1=δh+hδ3/v的角位移。五杆机构P点轨迹曲线的傅里叶表达式为
rP(t)′=[Rejμ+l4ejβ+l0c0ej(α+β+φ0)]+
l0c1ej(α+β+φ1+δ3/v)ejωt+l0c-1ej(α+β+φ-1-δ3/v)e-jωt+
[l3ej(δ3+β)+l0cvej(α+β+φv+δ3)]ejvωt…+
l0ckej(α+β+φk+kδ3/v)ejkωt+…
(17)
将式(17)中0次和v次谐波分量的系数分别进行合并,经整理得到rp(t)′的傅里叶系数
(18)
其中:Ck=ckejφk,k为谐波成分的次数,且k∈[-p,p],p为正整数。
4 基于傅里叶描述符的曲线拟合
首先,针对给定的期望轨迹点,傅里叶描述符理论上有无穷多项,但对于实际问题,我们采用有限阶数的傅里叶描述符[14],即可较好近似定义任务轨迹曲线R
(19)
其中:p为谐波成分的阶数,x(t)+jy(t)即为期望轨迹点R在复平面上的坐标,期望轨迹点傅里叶系数Rk的值可由第一节中的最小二乘法解出。
连杆机构工作点轨迹P通过有限阶数的傅里叶级数可以近似表示为
(20)
其中:p为谐波成分的阶数,Pk为连杆机构轨迹的傅里叶系数。当任务曲线R与连杆曲线P拟合时,满足
Rk=Pk,k∈[-p,p]
(21)
于是对于任务曲线R的傅里叶系数,满足
(22)
其中:Ck=ckejφk,从R的傅里叶系数我们观察到,R0、Rv、Rk均包含展杆参数l0ej(α+β),定义
(23)
即
K1+jK2=l0ej(α+β)
(24)
针对RRPRR型五杆机构的10个参数,我们设解集
M={l1、l3、l4、xa、ya、δ3、δh、K1、K2、β}
(25)
连杆机构各杆尺寸按比例缩放不影响连杆转角,为便于程序化求解,将解集M分别定义为解集
(26)
针对多参数的非线性优化问题,目前已经有粒子群算法、蚁群算法、遗传算法等算法,其中遗传算法是基于生物进化理论而产生的随机全局优化算法,该算法适合较复杂的优化问题,相比于传统优化算法,遗传算法可以获得很好的效果[15]。采用遗传算法计算系数Rk的最小二乘解,通过最小化误差函数I1,使任务曲线尽可能穿过所提供的目标点
(27)

(28)
即误差函数的取值与K1、K2无关,由此
(29)

通过优化算法对l3/l1、l4/l1、δ3、δh的值进行搜索后,当I1在许可误差范围内时,可得到解集M1{l3/l1、l4/l1、δ3、δh、K1、K2},同时也得到了Ckejkδ3/v的值,由式(22)中的v次谐波成分
Rv=l3ej(δ3+β)+Cvl0ej(α+β)ejδ3/v
(30)
将已知量带入式(30),分离实部和虚部后相除,消去l3即可获得β,后代入β即可获得l3。得到l3后代入解集M1即可得到l1和l4。
由式(23),根据已知K1、K2、β的值,可解出l0和α。
由式(22)中的0次谐波成分
R0=Rejμ+l4ejβ+C0l0ej(α+β)
(31)
通过代入已知参数,将式(31)分离实部虚部可得到Rejμ的值,因
Rejμ=xa+jya
(32)
由式(32)即可得xa和ya。
到此已解出l1、l4、l0、α,解集M2{l3、xa、ya、β}的全部参数,RRPRR型五杆机构的连杆参数已经全部解出。
5 综合实例
为进一步验证开式傅里叶描述符在连杆曲线拟合过程中的实际效果,给出了两个应用实例,分别为整周采样点下的拟合与开式曲线下的拟合。
5.1 整周采样点下的拟合
整周采样点下的拟合相当于拟合角度为360°,对于开式傅里叶描述符同样适用。给定32个期望轨迹点,如图3所示,对应位置的坐标见表1。

表1 期望轨迹的取样点坐标

▲图3 期望轨迹点
设定实例中曲柄AB和曲柄DC传动比ω1∶ω3为1∶1。根据给定的坐标点,使用MATLAB编写程序,利用遗传算法对坐标点进行拟合,拟合误差为1.0850e-05,拟合效果如图4所示。

▲图4 整周采样点下的拟合
从32个取样点中,计算不同阶数下的拟合误差,随机选取其中7个拟合点为例,列出不同阶数下轨迹点的拟合误差,如表2。

表2 各个位置点在不同阶数下的拟合误差
从表2中可以看出,当阶数k为3阶时,坐标点的拟合误差已经小于1%;当阶数为5时,拟合误差已经减少到0.5%以下。
5.2 开式曲线下的拟合
在某纸盒生产过程中,需要将纸张从纸张定位装置移送到纸堆,从而完成纸张的送料,如图5所示。

▲图5 纸张送料示意图
根据预定的纸张移动轨迹,从轨迹中选取16个点作为期望的轨迹点,并设曲柄AB和曲柄DC的传动比ω1∶ω3为1∶1,坐标点如表3。

表3 给定的拟合坐标点
因拟合的路径是开式曲线,我们需要设定其拟合的角度,分别为110°、120°、130°、140°,拟合效果如图6所示。
根据拟合的结果,当拟合角度为120°时,拟合误差最小,拟合效果满足预期,得出的数据如下:
通过分离实部和虚部,可以解出解集M2={l3、xa、ya、β},其中

▲图6 不同拟合角度的拟合误差
由K1、K2以及β的值,求解出α以及l0的值。
α=1.109 0,l0=3.810 6
由以上的公式,可以得知该拟合的RRPRR型五杆机构的10个参数,汇总如下:
机架原点A的坐标(xa,ya)为:(41.982 4,11.947 6);
曲柄AB的杆长为17.287 9 mm;
曲柄CD的杆长为13.200 1mm;
机架AD的长度为17.050 2 mm;
机架AD与x轴夹角β为0.460 6 rad;
曲柄AB初始角度δ1为1.137 4 rad;
曲柄CD初始角度δ3为0.209 3 rad;
连杆CP的长度为3.810 6 mm;
连杆CP与BC间夹角α为1.109 0 rad。
因此,本实例选用拟合角度拟合角度为120°时的机构作为纸张输送机构。
6 结论
研究采用基于傅里叶描述符的最小二乘法拟合连杆轨迹曲线,并给出了该方法在RRPRR型五杆机构开式曲线的拟合过程,取得了较好的拟合效果,为后续连杆机构开式曲线的拟合提供了可借鉴的方法。在综合案例中,采用的遗传算法通过给定不同的拟合角度对其进行拟合求解,从而获得满足预期结果的连杆机构。经过改造的傅里叶描述符克服了原有必须取样整周期采样点的连杆曲线拟合,更加符合实际工程应用。
