拨动式压电旋转发电机设计与测试
2023-09-18贺春山刘亚鑫盖厚君林佳颖田晓超
贺春山, 刘亚鑫, 盖厚君, 杨 杰, 林佳颖, 田晓超
(长春大学 机械与车辆工程学院,长春 130022,E-mail:hecs@ccu.edu.cn)
近年来,随着微机电系统及集成电路迅速发展,低功率电子设备广泛应用在各个领域,急需一种稳定、安全、寿命长的电源来满足电子产品的供电需求。由于传统锂电池无法满足微电子设备供电需求,特别是在能量密度、寿命和维护成本[1-2]等方面,低功率设备的普及引起了对供电方式的关注。目前,发电方式有很多种,如热电发电,静电发电,电磁发电,压电发电及摩擦发电。热电发电机可以将加热通量直接转化为电能,但体积较小,没有活动部件,并且造价昂贵、效率较低[3]。静电发电能以较小的结构尺寸输出高电压,但是需要较小的间隙和起始电压才能实现高功率密度发电,能量收集系统的更加复杂[4]。电磁发电系统有运行稳定和输出高电流的特性,受到低频激励时,输出功率密度低[5-8]。
摩擦发电系统具有高功率密度,存在电流密度低并且电荷收集困难[9]。压电发电因其能量密度高,机电耦合强,结构简单以及与微机电系统的兼容性强而受到广泛关注[10-18]。
目前国内外在压电振动能量收集器方面的研究,对形式各异的悬臂梁仍是研究重点[19-21]。Zhang等人[22]研制了一种用于风能收集的压电旋转发电机。Chen等人[23]研究了一种拨动式压电发电机,由转轴、风扇叶片、敲击杆和压电悬臂粱组成。Cheng Yan等人[24]设计了以螺旋连杆、定子、转子为基础的线性-旋转转换结构。
本文设计了一种拨动式压电旋转发电机,并从理论和实验两个方面进行研究,研究悬臂式压电振子和万向球数量及转速等对系统发电能力的影响规律。可以调节压电振子与万向球的数量来调节发电量。此微型发电机适用于各种转速较低的场合,收集的电量可以满足微小型功率电器的供电需求。
1 结构设计与工作机理
压电旋转发电机的结构示意图如图1所示,主要由悬臂式压电振子、万向球、轴承、旋转轴、顶板和支座组成。压电陶瓷材料双面贴置在金属基板上,为双晶片压电振子。支座上嵌入万向球,起到拨动压电振子变形的作用。当旋转轴转动时,带动顶盘旋转进而带动压电振子旋转,旋转的压电振子与万向球接触,压电振子被万向球拨动进而发生形变,由于压电材料的正压电效应,压电陶瓷表面产生电荷,进而起到发电效果。
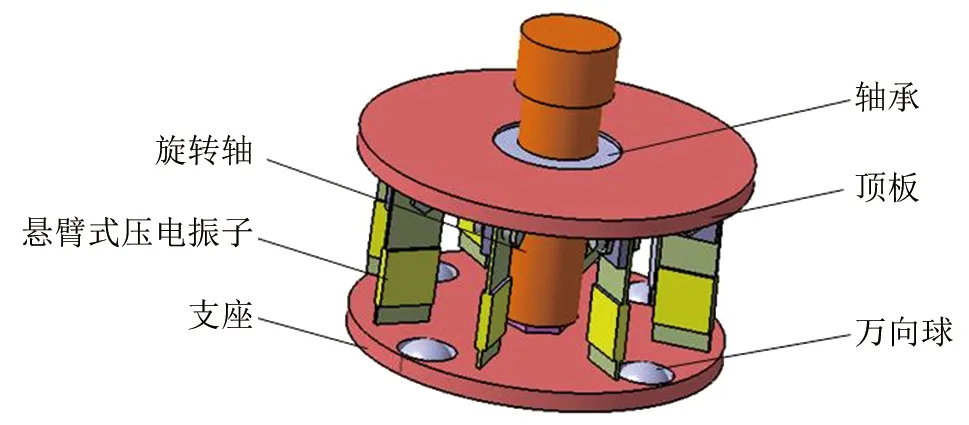
▲图1 压电旋转发电机结构示意图
2 理论建模与仿真分析
2.1 理论建模
压电旋转发电机系统的动力学方程为:
Mx″+Cx′+Kx∑θv=F
(1)
(2)
式中:M为系统等效质量;C为等效阻尼;K为压电振子等效刚度;θ为压电振子等效机电耦合项;Cp为压电层等效电容;RS为压电振子等效电阻;v为等效电阻两端电压;x为发电机在横向方向上的尖端位移;X为外部作用力。
外部作用力为:
F=mg+Fmn
(3)
式中:m为压电振子等效质量;g为重力加速度;Fmn是压电振子与万向球碰撞时的弯曲力。
压电旋转发电机在外部作用力F下的开路输出电压为:
(4)
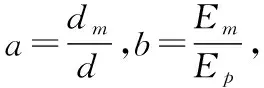
c=a4(1-b)2-2a(2a2-3a+2)×(1-a)+1
其中:g31为压电电压系数;dm为金属基板厚度;d为压电陶瓷厚度;Em为金属基板的杨氏模量;Ep为压电陶瓷的杨氏模量;lp为压电振子长度;Wp为压电振子的宽度。
将式(3)代入式(4)得:
(5)
由式(5)可以得出,发电机输出电压与压电振子与万向球碰撞时的弯曲力以及速度有关。
压电梁产生的功率P为:
(6)
式中:R1为负载电阻;Rs为压电片元件等效电阻。
2.2 仿真分析
采用压电陶瓷是PZT-5,金属基板选用铍青铜,压电陶瓷和金属基板采用矩形结构。压电陶瓷和铍青铜材料参数如表1所示。压电陶瓷和铍青铜尺寸参数如表2所示。

表1 压电陶瓷和铍青铜材料参数表

表2 压电陶瓷和铍青铜尺寸参数表 mm
PZT-5的刚度系数矩阵(单位×109Pa)、压电系数矩阵(单位×10-12C/N)、介电常数矩阵(单位×10-9F/m)为:
通过对压电振子的仿真,得出压电振子一阶共振频率为147 Hz,代入式(3)可求得压电振子自由端受到的作用力,得出仿真结果如图2所示。
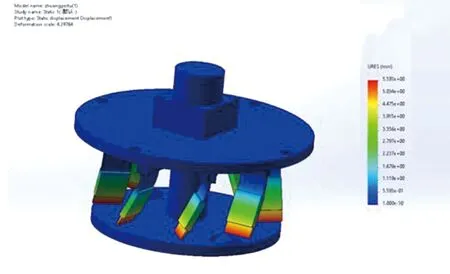
▲图2 系统仿真结构图
在压电振子一阶共振频率下,压电振子自由端最大位移为5.594 mm。
通过式(5)可以计算出单个压电振子单个万向球输出电压与自由端位移的关系如图3所示。转速与电压的关系如图4所示。
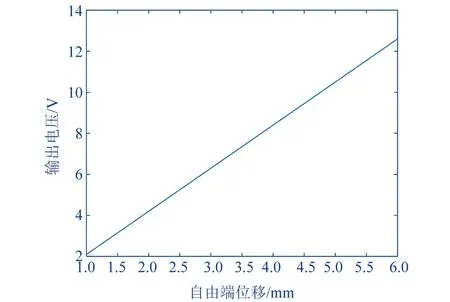
▲图3 输出电压与自由端位移的关系图
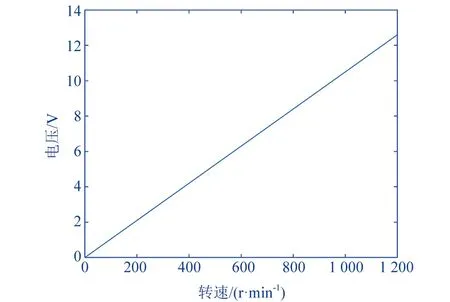
▲图4 转速与输出电压的关系图
从图中可以看出输出电压分别与转速、自由端位移成正比。
3 实验测试
3.1 测试装置
实验测试装置如图5所示。主要由示波器、旋转发电机样机、支撑架以及驱动电机组成。驱动电机用于驱动顶盘转动。

▲图5 实验测试装置
3.2 自由端位移转速与输出电压的关系
当压电振子个数为1,万向球数量为1时,不同压电振子自由端位移转速与输出电压的关系如图6所示。
从图中可以看出,当转速增大时,输出电压随自由端位移的增大而增大,而自由端位移越大,输出电压越高。由于考虑到压电振子脆性较大,不易产生较大形变,故对自由端位移进行限制。当转速达到1 200 r/min时,输出电压最大为12.6 V。
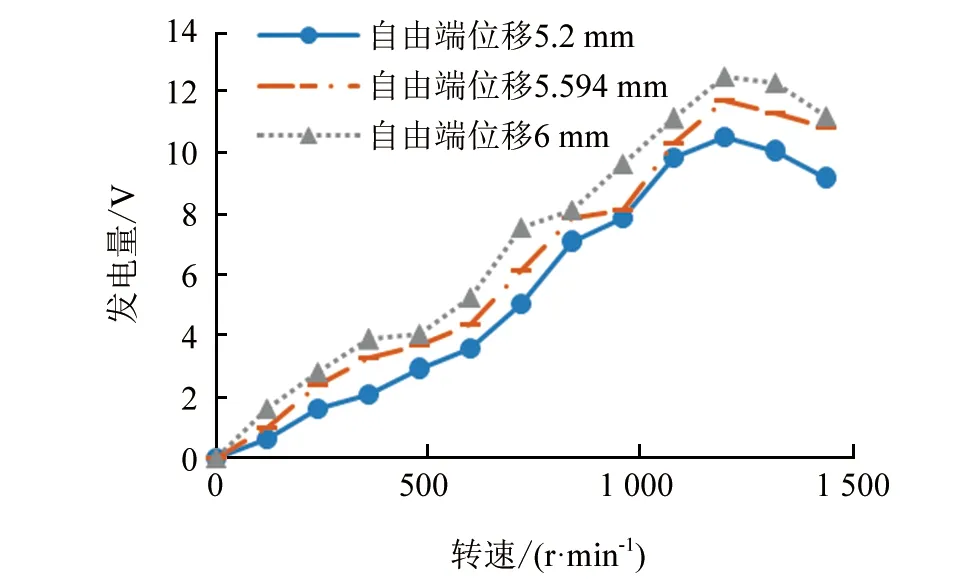
▲图6 不同压电振子自由端位移转速与输出电压的关系图
3.3 不同数量万向球转速与输出电压的关系
通过自由端最大位移进而确定万向球位置,当自由端最大位移为6 mm,压电振子个数为1时,不同数量的万向球转速与输出电压的关系如图7所示。
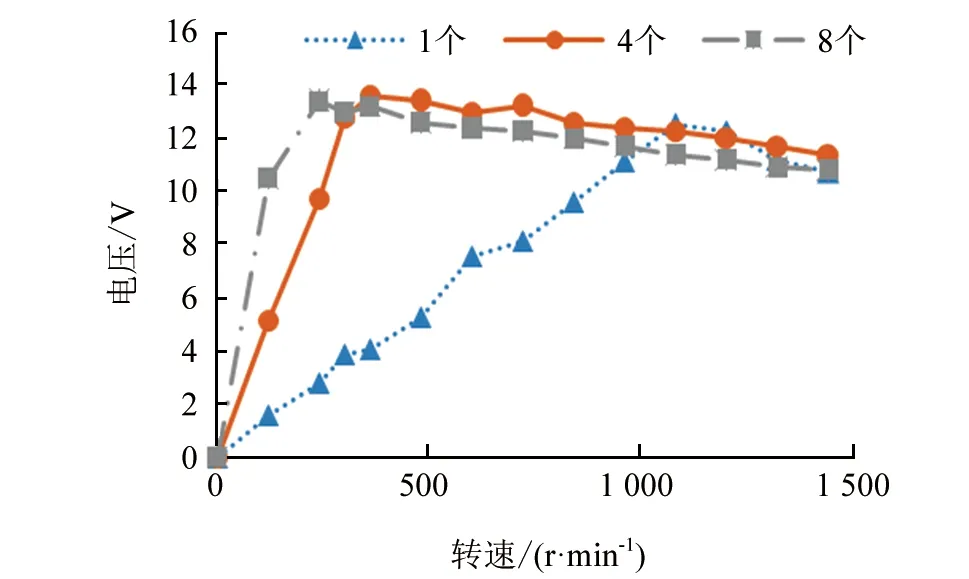
▲图7 不同数量万向球转速与输出电压的关系图
从图中可以看出,当万向球个数为4时,输出电压最高可达13.7 V。万向球不宜过多,这是由于在转速达到一定后,由于万向球过多,压电振子未来得及回弹就与下一个万向球相撞击,压电振子的形变量减小,输出电量会减小。
3.4 不同数量压电振子转速与输出电压的关系
当自由端最大位移为6 mm,万向球个数为4时,不同数量压电振子转速与输出电压的关系如图8所示。
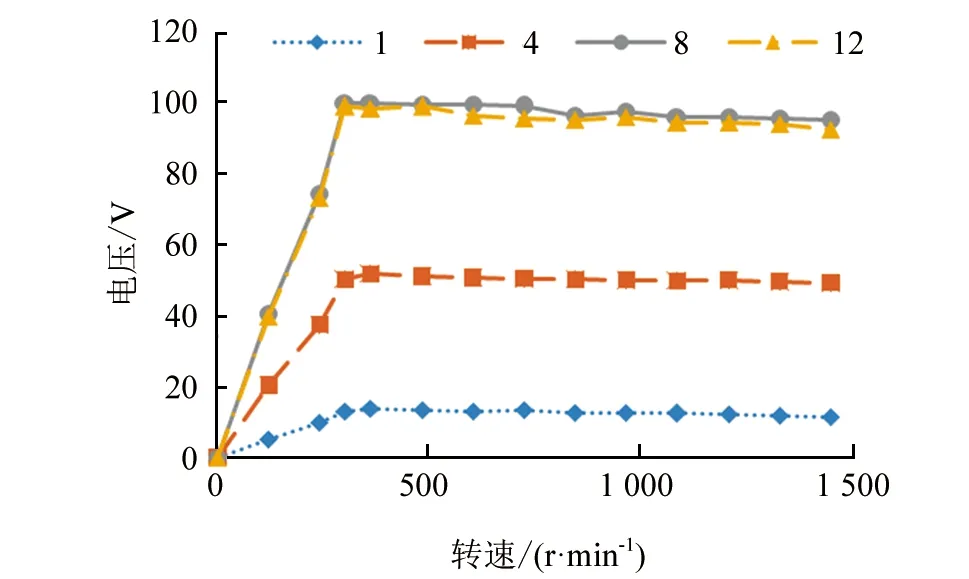
▲图8 不同数量压电振子转速与输出电压的关系
从图中可以看出,当压电振子数量为8时,输出电压最高为99.6 V。压电振子不宜过多,因为压电振子数量过多时,自由端产生的位移互相干涉,无法形成最大位移,变形受到限制,输出电压会降低。
3.5 输出功率与负载电阻的关系
由公式(6)可知,平均功率随着电压的增加而升高。当万向球个数为4、压电振子个数为8、自由端位移为6 mm时,对平均功率的理论值与实验值进行分析。本实验电路中各内阻之和约为60 KΩ。
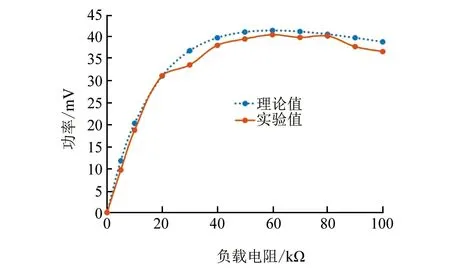
▲图9 输出功率与负载电阻的关系曲线
从图中可以看出当负载电阻与电路内阻一致时,输出功率达到最佳为40.36 mW,理论值与测量值相符。
4 结论
通过理论与仿真分析得出了压电旋转发电机的输出电压与压电振子数量、万向球数量及压电振子自由端位移的关系。当压电振子质心旋转半径为45 mm时,自由端位移为6 mm,压电振子个数为8,万向球个数为4时,压电旋转发电机具有最佳的发电性能,输出电压可达99.6 V,输出功率为40.36 mW。可满足低功率微电子设备的供电需求。
