物流AGV机器人行驶动态特性分析
2023-09-18吕世霞朱亚东
吕世霞, 王 枭, 朱亚东
(1.北京电子科技职业学院 汽车工程学院,北京 100176,E-mail: lv675367979@126.com;2.北方工业大学 机械与材料工程学院,北京 100144;3.北京石油化工学院 机械工程学院,北京 102617)
国内外诸多智能制造工厂已将物流AGV(Automated Guided Vehicle)机器人作为搬运货物的主要工具,而机器人的行驶动态特性是整车性能评价的重要指标,不仅直接影响车载仪器设备的稳定性和行驶安全性,还间接影响到机器人的动力性、经济性及零部件使用寿命等指标[1],合理的悬架系统参数匹配对改善机器人的行驶动态特性具有重要作用。对悬架设计而言,传统的悬架参数匹配主要是通过设计人员的经验和理论模型分析法来实现的,随着数值模拟技术的发展,运用虚拟样机平台与试验设计相结合对悬架参数进行优化,并进行行驶平顺性分析[2-4],这种方法以其真实可靠、精度高等特点,成为研究机器人等移动平台行驶动态特性较常采用的方法。
谢步庆设计了一种轮式移动机器人,建立了整机悬架系统振动模型,优化了悬架系统结构参数,为机器人行驶平顺性提供了有效的悬架系统参数[5]。刘晋浩等设计了一款具有减振性能的草方格铺设机器人,建立了整机系统动力学模型,进行了机器人平顺性评价[6]。Caicedo等基于悬架系统动力学模型,研究了不平路面激励对车身稳定性影响[7]。上述研究所建模型较为简单,精度较低,同时未对机器人行驶动态特性进行深入分析。
本文设计了一种应用于物流AGV机器人的悬架系统,采用参数可调的独立驱动转向的纵臂式结构,建立整车的四轮系振动耦合响应模型及悬架参数优化模型,并进行仿真与试验研究。
1 物流AGV机器人移动系统结构设计
物流AGV机器人结构如图1所示,其驱动机构由四个舵轮构成,机器人具有高灵活性的特点,满足仓储车间等较复杂环境的使用要求。由于路面激励等产生的振动会导致轮子出现行走偏差,影响机器人的运动控制。通过为每个驱动机构设计独立悬架,从而降低路面激励对机器人造成的振动影响,实现平稳转运。

▲图1 物流AGV机器人结构图
由于悬架机构采用被动式减振器,不具备主动改变机构减振性能的条件,故在机构的底部增加了调节块,通过改变减振器角度以及纵臂长度来调节悬架系统参数,提高机构的适应性。悬架系统结构如图2所示,支架结构通过中间码盘与从动齿轮相连,前端与减振装置通过横辊相连,后端与纵臂铰接。当路面不平度激励作用车轮上时,支架结构由于减振装置作用会产生相对车轮回转中心的俯仰运动,支架结构承受纵臂与减振器的支反力,同时支架具有较长距离的悬臂特性。与传统结构相比,所设计的舵轮悬架系统具有高度集成、高空间利用率等优点,能够充分保证物流AGV机器人的运动性能。

▲图2 悬架系统三维模型与物理样机
2 动力学模型的建立
2.1 路面激励建模
根据机器人行驶在随机路面的实际情况,将机器人行驶状态分为匀加速、匀速、匀减速三种状态。在加速时,加速度恒定;当加速度为0时,位移与时间呈现线性变化;当加速度为小于0的常数时,位移为时间的二次多项式,综合描述如公式(1)。
(1)
式中:Vv为最大速度;Ta为加速时间段。
基于高斯白噪声的振动系统输入与输出关系[8]:
(2)
式中:v为车速;f0为下截止空间频率,取0.011 Hz;w(s)为空间域内均值为零的Gauss白噪声,功率谱密度Gq(n0)取0.64×10-6m3,n0取0.1/m。
基于式(2)进行路面激励建模,其功率谱密度与标准路面具有良好的一致性[9]。设左前轮、右前轮、左后轮和右后轮的空间域路面不平度为q1(s)、q2(s)、q3(s)、q4(s),根据时间—空间域之间的变换关系以及相关函数等效法进行换算,得到左前轮路面非平稳激励的时域方程:
(3)
式中:w(t)为时间域内均值为零的Gauss白噪声。
基于Bogsjo提出的描述左前轮与右前轮与之间的时域相关函数coh(n)[10]:
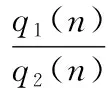
(4)
式中:B为左右轮的轮距。
根据时间域和空间域之间的变换关系以及指数函数的一阶Pade逼近[11]和傅里叶逆变换,可以得到右前轮、左后轮和右后轮路面非平稳激励的时域方程:
(5)
(6)
(7)
(8)
式中:L为前后轮的轮距。
根据式(5)、(6)、(7)、(8),进行数值建模,如图3所示。
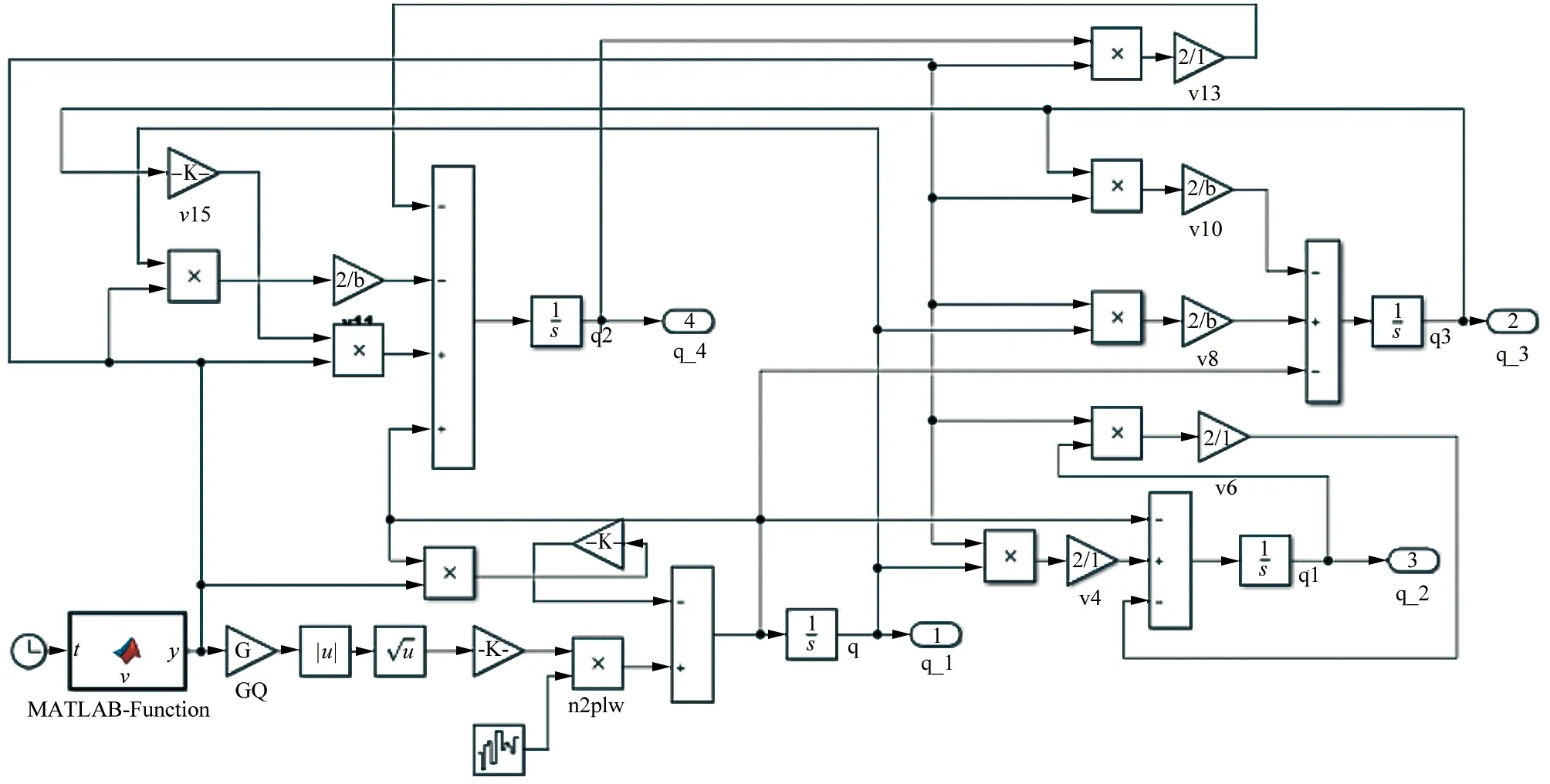
▲图3 四轮普通路面激励模型
2.2 动力学建模
机器人行驶时,轮系及悬架系统受到路面的冲击,使车体产生耦合的振动响应,其中车身垂向加速度、侧倾角加速度、俯仰角加速度、悬架动挠度、车轮动载荷是研究机器人行驶平顺性较常用的评价指标[12],一般垂向加速度能够直观体现机器人的垂直方向上振动幅度大小,路面左右或者前后发生变化会引起侧倾角加速度或俯仰角加速度的变化;悬架动挠度、车轮动载荷更多是机械结构的约束,从结构设计上保证悬架伸缩行程大于悬架动挠度,而车轮动载荷如果过大则会对车轮造成破坏,太小会使车轮出现悬空问题。
将图2所示悬架系统简化为具有线弹性系数的弹簧和一定阻尼的阻尼器。兼顾四个非悬挂质量的四个垂向自由度,进而建立整车的四轮系振动耦合模型[13]如图4所示。

▲图4 四轮系振动耦合响应模型
四轮系振动耦合响应模型由地面、轮胎、悬架系统及车身组成,图中的相关参数如表1所示。
表1 四轮系振动响应模型参数表
四轮系振动耦合响应模型的动力学微分方程可以通过矩阵形式表示:
(9)
式中:[M]为质量矩阵,[C]为阻尼矩阵,[K]为刚度矩阵,[Kz]为输入系数矩阵,q为路面输入。
假设机器人直线行驶,速度恒定,根据牛顿第二定律,可得到机器人车身垂直方向的运动微分方程:
(10)
机器人侧倾运动微分方程:
(11)
机器人俯仰运动微分方程:
(12)
悬架下端垂向运动微分方程:
(13)
每个轮系的簧载质量产生的位移及速度:
(14)
根据方程(10)、(11)、(12)、(13)、(14),进行数值建模,如图5所示。

▲图5 系统反馈模块
3 悬架系统参数优化设计
3.1 设计变量的确立
通过选择合理的悬架刚度系数和阻尼系数以降低路面激励对机器人造成的振动影响,实现安全、平稳转运。因此,将弹簧等效刚度系数k、阻尼元件等效阻尼系数c作为优化模型的输入参数。
3.2 目标函数的确立
(15)
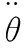
(16)
式中:a为加权加速度。
3.3 约束条件的确立
为了保证机器人行驶的平顺性以及减振系统的有效性,设计变量和状态变量需要满足一定约束条件。机器人设计变量约束条件:
机器人悬架系统的固有频率取值范围为[2.5,6.5],因此,可得到悬架固有频率的约束[15]:
(17)
根据机器人工作情况,同时兼顾行驶平顺性和稳定性,对悬架系统阻尼比取极值,得到阻尼比的取值范围:
(18)
式中:rm为轮子刚度与悬架刚度之比,rk为簧上质量与簧下质量之比。
由机器人基本设计参数可得,车身侧倾、俯仰转动惯量24.6 kg·m2、93.4 kg·m2,簧上质量400 kg,每个减振舵轮重20 kg,轮子刚度2 000 000 N/m,前后轮距1.43 m,左右轮距0.50 m,代入式(17)、(18)可得悬架刚度系数取值范围为[12 324,83 314],阻尼系数的取值范围为[557,4 833]。
3.4 优化结果分析
基于最小二乘法参数辨识方法是求解线性或非线性系统等多种数学寻优问题较常用的方法[16]。经过14次迭代计算收敛,迭代过程如图6所示。初选弹簧刚度系数k=80 000 N/m,阻尼元件的阻尼系数c=1 500 N·s/m;寻优后,刚度系数k=40 012 N/m,阻尼系数c=1 002 N·s/m。
4 对比分析
基于MATLAB/Simulink建立的连续普通路面模型,结合机器人实际行驶时的工作环境和状态参数,在MATLAB-Function模块中设置初始时刻t0=0 s,最大速度Vv=0.5 m/s,总加速时间为30 s,加速时间段Ta=10 s。模拟机器人满载直线行驶在B级普通路面,Gq(n0)=64×10-6m3,机器人行驶状态为前10 s加速行驶,10 s~20 s匀速行驶,20 s~30 s减速行驶。机器人仿真分析下不同响应量时域波形如图7所示。
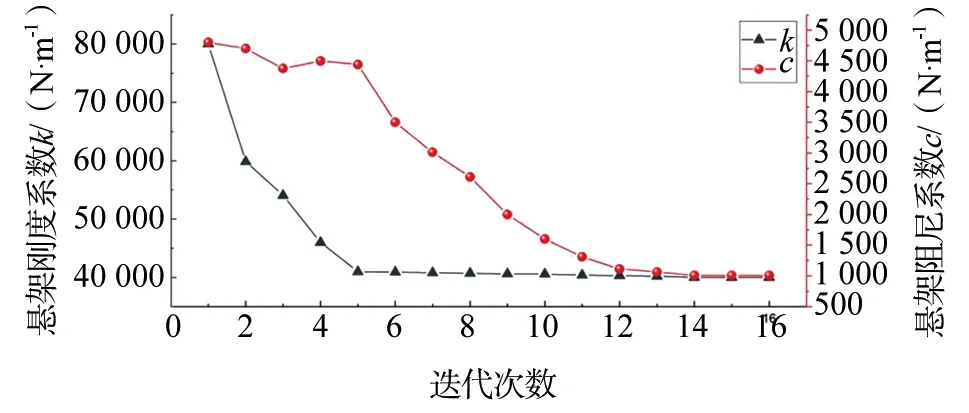
▲图6 刚度系数和阻尼系数迭代过程
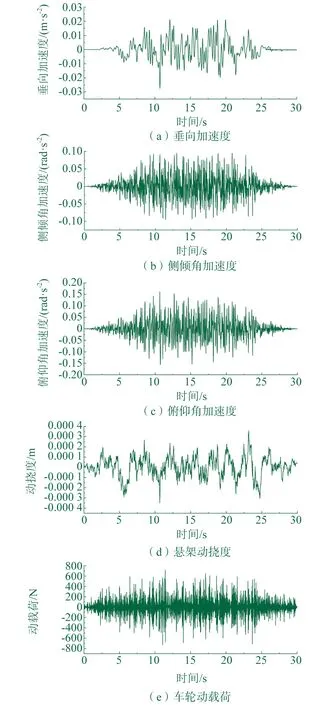
▲图7 机器人仿真分析是不同响应量时域波形

▲图8 试验系统搭建
试验时,将加速度计布置方案如图8所示,分别放在车体上表面几何中心、舵轮悬架上顶板以及车体上表面前后左右两端对称各布置一处。启动无线测量系统记录加速度时间历程,数据采集时长50 s,采集10次,采样率f=40 Hz,负重采用等重量的实验室相关设备代替,机器人以加速度0.05 m/s2满载直线行驶在普通路面,最终处理数时保证其加速、匀速、减速时间分别为10 s。绘制车体振动响应量时域波形如图9所示。
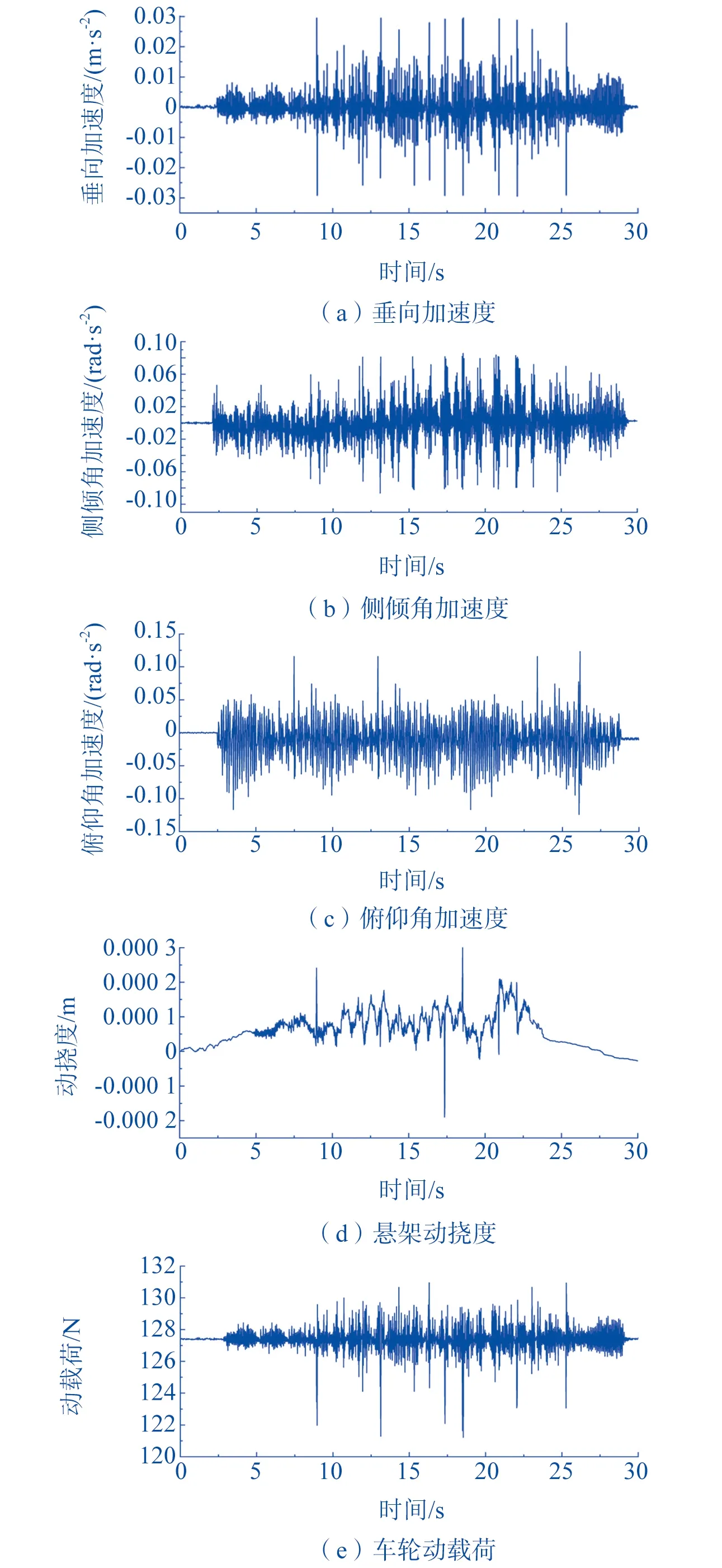
▲图9 机器人试验测试时不同响应量时域波形
对图7、图9中各个振动响应量的数据进行量化分析,计算出有效值和最大值如表2所示。
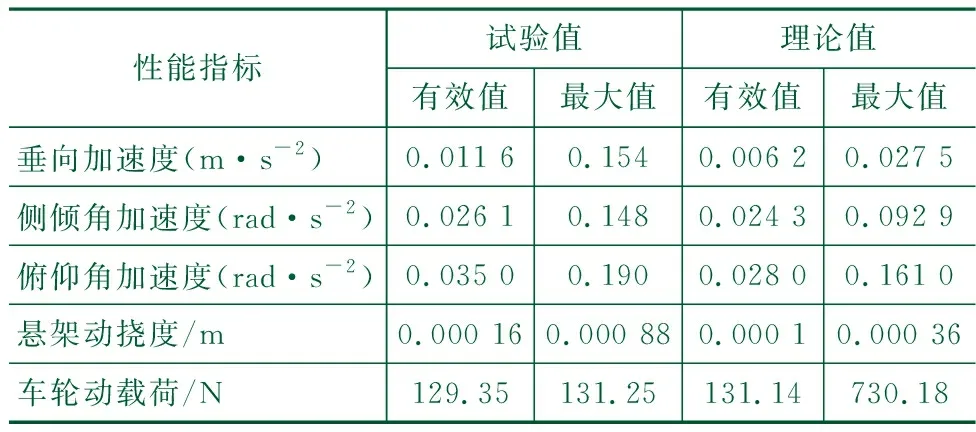
表2 振动响应量的考量指标

表3 车体行驶平顺性的评价表
以ISO2631制定的均方根值法对机器人的平顺性能进行定性评价[17]。将优化前后车身三个方向的加速度进行加权处理:
(19)

进一步对机器人的有效值进行量化对比分析,仿真分析与试验测试的加权加速度数值分别为0.052 m/s2和0.055 m/s2,实际测试的机器人行驶加权加速度值比理论值要大,同时对比仿真分析和试验测试获得的各个振动响应量有效值,可以看出,左前车轮动载荷和后悬架动挠度试验测试获得有效值要小于理论仿真值,其余的各个振动响应量试验测试的有效值均大于仿真值,这是因为在悬架系统机械加工时,调大了些悬架系统刚度与阻尼值,并且仿真模型与试验样机的约束载荷分布也可能有一定出入,但垂向加速度试验测试有效值、最大值与理论仿真有效值、最大值误差分别约为6.4%、7.2%<8%,较优于文献[18]。
仿真分析与试验测试的加权加速度数值均小于0.315 m/s2,人体主观感觉没有不舒适,评价仍然为优,与理论加权加速度值具有良好的一致性,表明对悬架系统建模分析是合理的,进一步说明所建立悬架系统能够有效改善系统行驶动态特性。
5 结论
(1) 所设计的独立驱动转向的纵臂式悬架结构形式简单、通用性良好,在B级路面可以有效提高物流AGV机器人的平顺性和稳定性。
(2) 基于最小二乘法参数辨识方法进行了悬架系统参数调校,仿真与试验结果表明,试验加权加速度值与理论加权加速值均在最优水平,两者具有良好的一致性,验证了对悬架系统建模分析的合理性。
(3) 所构建的整车四轮系振动耦合响应模型为移动机器人在结构化道路下的平顺性优化设计提供了理论依据。
