横置椭圆形砂岩隧洞裂纹扩展特征与破坏征兆研究
2023-09-15朝文文徐培元张黎明王建新张素磊王在泉
朝文文, 徐培元, 张黎明, *, 王建新, 张素磊, 王在泉, 丛 宇
(1. 青岛理工大学理学院, 山东 青岛 266033; 2. 青岛理工大学土木工程学院,山东 青岛 266033; 3. 应急管理部国家自然灾害防治研究院, 北京 100085)
0 引言
水利、交通、矿山领域的地下工程建设中,受外部荷载及开挖卸荷过程应力重分布影响,围岩坍塌、冒顶、片帮问题频现[1-3]。将隧道(洞)围岩简化为含孔洞岩体试样,国内外学者对其裂纹扩展规律和破坏机制进行了大量的理论、试验和数值模拟研究。杜明瑞等[4]对含预制椭圆形孔洞板状砂岩进行了单轴压缩试验,发现岩样以剪切破坏为主,椭圆长短轴比增加,峰值强度降低。周亚楠等[5]对含充填椭圆形孔洞板状砂岩进行单轴压缩试验,发现随着充填物力学性能的增强,岩样的破坏模式由拉伸破坏向剪切破坏转变。李地元等[6]对含不同形状孔洞的大理岩进行单轴压缩试验,发现椭圆形岩样先在孔洞拱顶和拱底同时形成2条平行于加载方向的拉伸裂纹,最终岩样由1条剪切主裂纹和1条拉-剪混合裂纹贯通发生破坏。段进超等[7]利用MFPA2D软件对含单孔和双孔脆性材料单轴压缩下的破坏过程进行模拟,发现初始裂纹不一定是最后形成宏观贯通破坏的主裂纹,且非均质性是岩石类脆性材料发生局部破裂的根本原因。Zhong等[8]利用RFPA2D数值模拟含倒U形孔洞流纹岩的双轴压缩试验,发现在孔洞侧壁形成哑铃状压应力集中区,且孔洞转角处更容易产生压缩裂纹。
岩体破坏具有某些征兆,学者们对岩石破坏前兆进行了多角度的研究。张艳博等[9]采用可见光图像和远红外相结合的监测手段建立了岩爆监测的多物理场参数联合预警方法,发现可见光图像对岩爆的响应最为敏感。王创业等[10]对花岗岩单轴压缩试验过程中的AE时频域各特征参数进行联合分析,发现各参数的前兆响应时间存在差异,主频出现前兆特征时间较早,累计事件数出现前兆特征最晚。Liu等[11]采用DIC技术对含有双椭圆形孔洞砂岩进行单轴压缩试验,发现高应变局部化区域对应裂纹可能萌生的位置,裂纹扩展过程是高应变局部化区域的逐渐演化过程。Li等[12]利用声发射技术和DIC(digital image correlation)对含圆形孔洞花岗岩试样进行单轴压缩试验,发现试样的力学特性、表面应变场和声发射活动表现出一致性,声发射能量加速释放可作为岩石破坏的预警现象。此外,热红外技术[13-14]、电磁辐射技术[15]在岩体破坏预兆方面也进行了相关研究。
岩体破坏前兆现象复杂,识别困难,仅从单一角度识别破坏前兆信息有很大的局限性。因此,采用多种监测方法对岩体破坏进行综合预警具有重要的工程指导意义。学者们开展了大量小尺寸含孔洞岩样试验,但鲜有涉及大尺寸真实岩体隧洞试样破坏的试验研究;此外,传统的监测手段有限,在数据的采集及处理方面具有较大的局限性。
因此,本文开展大尺寸横置椭圆形真实砂岩隧洞模型试验,利用声发射测试系统和DIC测试方法解析横置椭圆形隧洞的渐进破坏过程,阐明横置椭圆形隧洞的表面裂纹和应变场演化规律,定量描述隧洞裂纹扩展过程中的分形特征,解译隧洞破坏时的不同物理场前兆信息。
1 椭圆形洞室试样双轴压缩试验
1.1 模型制备
在某地下能源储备洞库现场人工挖取大尺寸天然砂岩块体,为减小模型边界效应对试验结果的影响,确定模型几何相似比CL=15,容重相似比Cγ=1∶1。模型尺寸为500 mm×500 mm×100 mm(长×宽×厚),用水刀开凿贯穿试样的椭圆形孔洞,椭圆形长轴为110 mm、短轴为95 mm。隧洞原型及模型示意图见图1。
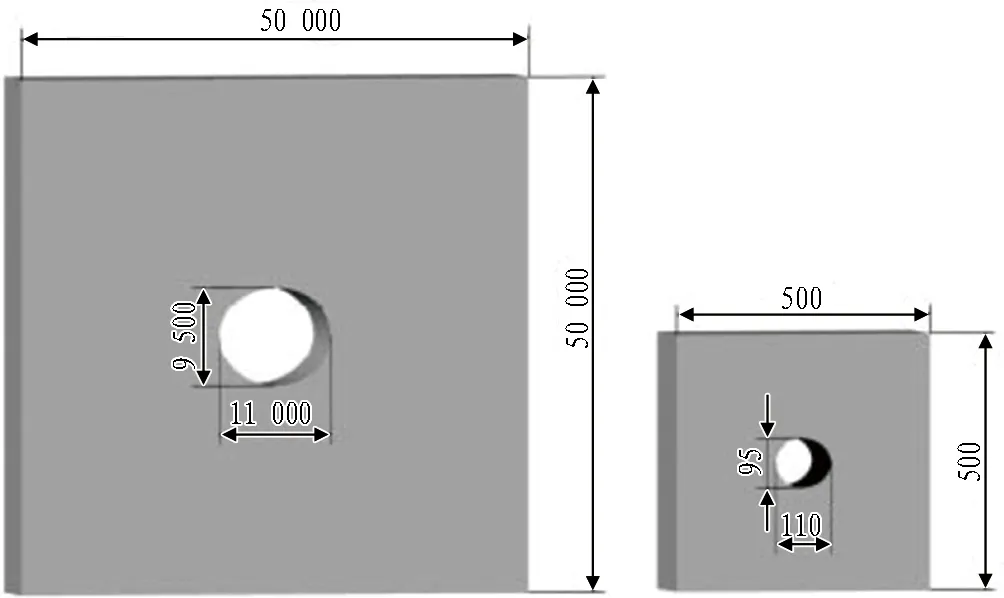
图1 隧洞原型及模型示意图(单位: mm)
采用单轴、巴西劈裂等试验测得砂岩干密度为2.65 kg/m3,弹性模量为9.1 GPa,内摩擦角为37°,黏聚力为9.60 MPa,泊松比为0.21,抗拉强度为4.6 MPa,单轴抗压强度为38 MPa,3 MPa围压下的完整砂岩强度约为43.9 MPa。
1.2 加载装置与监测系统
试验在岩石三轴试验机上完成,试验机能实时监控隧洞的荷载、变形信息,如图2所示。在隧洞模型左右两侧放置钢压板与液压泵相连,通过液压泵施加围压。为保证隧洞受力均匀,隧洞顶部、底部各垫设1块800 mm×300 mm×30 mm(长×宽×厚)钢压板,钢板和隧洞上、下、左、右4个侧面均涂抹凡士林油以减小摩擦。试验机竖向加载柱中心与隧洞中心在一条垂线上,防止隧洞偏心受压。
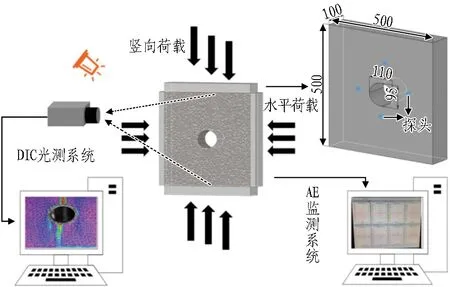
图2 试验加载装置与监测系统(单位: mm)
采用DIC光测技术记录隧洞表面位移场信息。隧洞表面用黑白哑光漆制作直径2~3 mm随机分布的黑色点状散斑。隧洞正前方放置1台高速摄像机,设置相机的拍摄分辨率为1 616 pixel×1 682 pixel,拍摄范围约为圆形孔洞洞周12×9 cm2,以1 fps速度拍摄试验过程。采用PCI-2型AE设备监测隧洞变形过程中的声发射现象,在隧洞背面洞周粘贴声为发射探头,门槛值为32 dB,2/4/6前置放大器增益值40 dB,采样频率为1 MHz。
1.3 加载方案
隧道开挖过程中,随着掌子面的推进,隧洞围岩承受的应力逐渐增加,因此设计竖向荷载采用分级加载并保载的方式。对同批次其他试件相同环境下进行单轴压缩预加载试验,通过计算3个试件的平均值得到该批次模型的极限承载能力为20 MPa左右。
隧洞双轴加载试验应力路径如图3所示。隧洞两侧施加围压3 MPa,竖向荷载Fz加载路径为: 采用应力控制,按照0.01 MPa/s的速度增加轴向应力至15 MPa,保载200 s;然后,通过位移控制方式以0.02 mm/min的速度每级增加荷载100 kN,并保载300 s,循环该加载过程,直至隧洞发生破坏。试验过程中,同步记录隧洞变形全过程的荷载、声发射和DIC光测试验数据。
2 隧洞裂纹扩展及应变场演化特征
2.1 隧洞表面宏观裂纹及应变场演化过程
隧洞表面宏观裂纹和应变场演化过程如图4所示。图中1—8代表裂纹萌生顺序,实线和虚线分别代表隧洞裂纹、表面岩体鼓起的轮廓线,裂纹角度为裂纹与水平方向夹角。
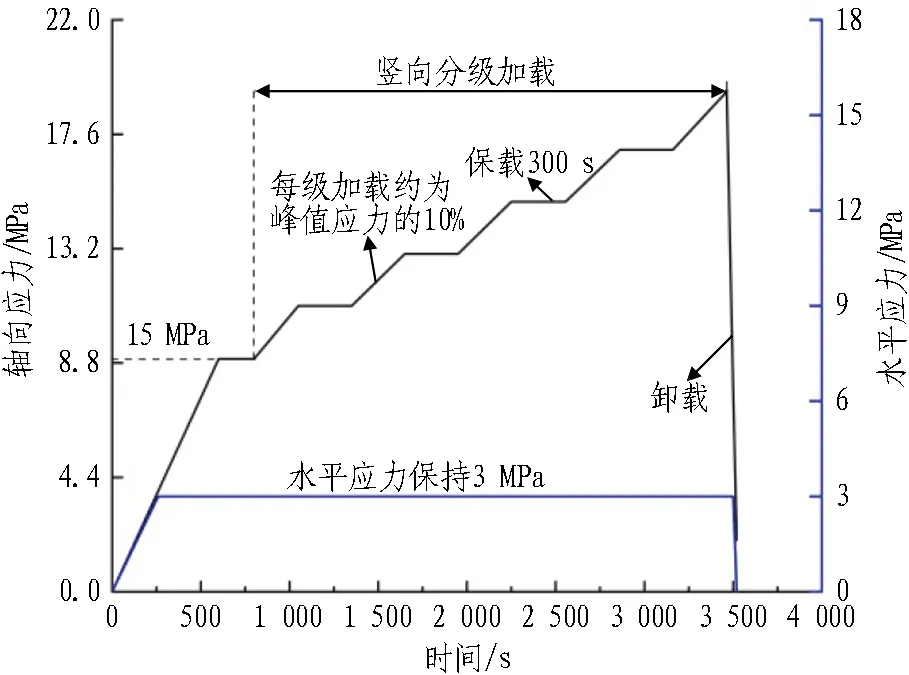
图3 隧洞双轴加载试验应力路径
1)加载至第1级荷载,t=938 s(轴向应力为8.9 MPa)时,隧洞表面无裂纹萌生,拱顶和拱底出现新应变集中区,范围小、量值较低,为0.001~0.005,如图4(a)所示。
2)t=938~1 566 s(轴向应力为8.9~13 MPa)时,处于第1级加载及保载过程,如图4(b)所示。拱顶、拱底分别出现1条竖向发展的张拉裂纹1和张拉裂纹2,长度分别为6、3 cm。此时,拱顶正上方和拱底下方均对应出现应变集中区,量值为0.003 0~0.006 8;而左拱腰出现1个椭圆形、小范围应变集中区,量值为0.002~0.003。
3)t=1 566~1 918 s(轴向应力为13~14.58 MPa)时,处于第2级加载及保载过程,如图4(c)所示。裂纹1、裂纹2未扩展。应力向两侧远端转移,在隧洞距左拱腰3 cm处出现1条沿80°斜向右下发展的剪切裂纹3,长度约12 cm。拱顶上方应变集中区无明显变化;拱底下方应变集中区范围缩小,量值减小为0.002 2~0.006 1;左拱腰原有椭圆形应变集中区沿80°斜向右下发展,量值为0.002 8~0.006 4。
4)t=1 918~2 218 s(轴向应力为14.58~15.6 MPa)时,处于第3级加载及保载过程,如图4(d)所示。裂纹1在剪切裂纹3出现后停止扩展,裂纹2闭合; 裂纹3从上端发展至隧洞洞口,长度增至14 cm。隧洞表面右侧壁上发生了细小岩块的剥落现象,同时隧洞右上方新萌生从上向下发展的远场裂纹4,与裂纹1平行,长度约6 cm。隧洞左拱腰应变集中区范围变大,量值增大为0.003~0.011;右上方出现新应变集中区,量值较低,为0.003~0.007 5。
5)t=2 218~2 487 s(轴向应力15.6~16.06 MPa)时,处于第3级保载过程,如图4(e)所示。裂纹1无明显变化,裂纹3沿下端向下发展至15 cm; 裂纹4下端沿120°发展至隧洞洞口,与附近微小裂纹贯通切割表面岩体剥落,岩体沿右侧洞壁向洞室底部滑落。隧洞右下方萌生远场裂纹5,长度约6 cm。隧洞拱顶应变集中区量值减小为0.001~0.006,但左、右两侧拱腰应变量值均有增大,分别为0.005~0.018、0.010~0.017。

(a) t=938 s,Fz=445 kN

(b) t=938~1 566 s,Fz=650 kN
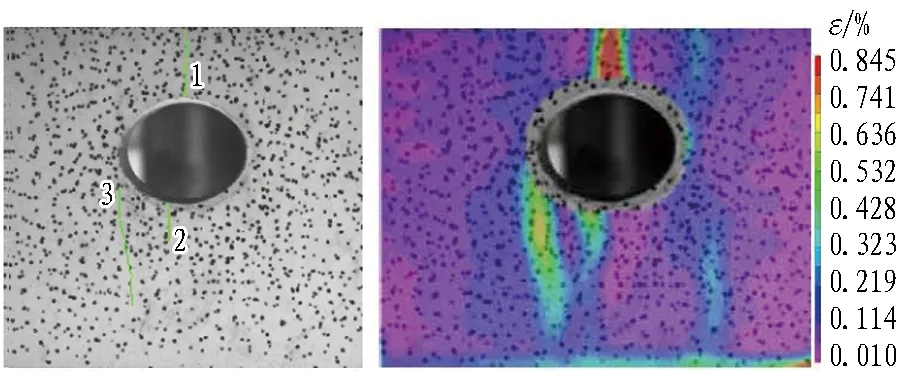
(c) t=1 566~1 918 s,Fz=729 kN
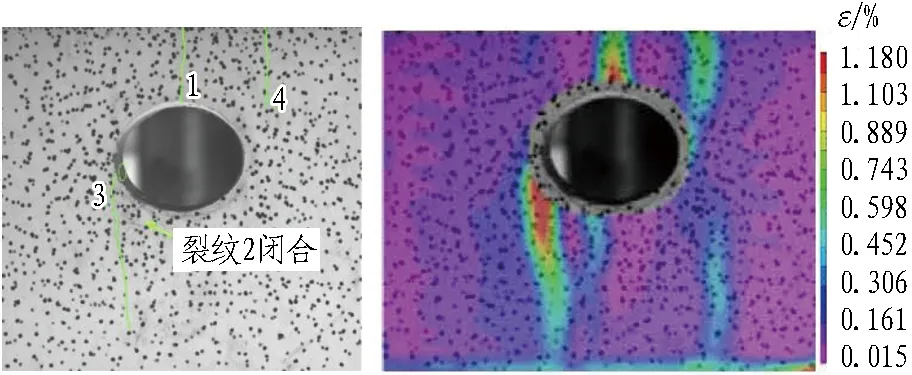
(d) t=1 918~2 218 s,Fz=780 kN
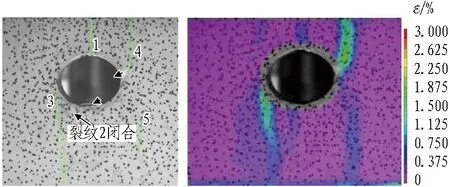
(e) t=2 218~2 487 s,Fz=804.38 kN
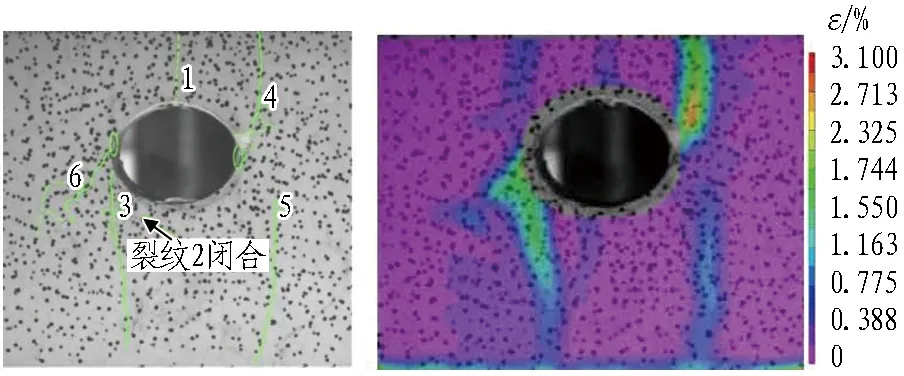
(f) t=2 487~3 094 s,Fz=917.11 kN
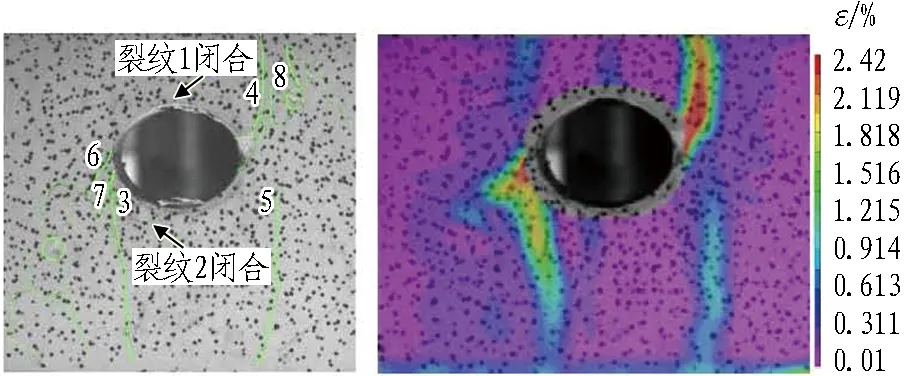
(g) t=3 094~3 462 s,Fz=961.41 kN
6)t=2 487~3 094 s(轴向应力16.06~18.34 MPa)时,处于第4级加载及保载过程,如图4(f)所示。裂纹3无明显变化,裂纹1宽度变窄,裂纹4附近出现微裂纹且岩体表面轻微鼓起,裂纹5继续竖直向下发展至长度14 cm。隧洞左侧拱腰处萌生1条沿150°斜向左下方发展的剪切裂纹6,且裂纹6下端附近岩体表面发生轻微鼓起。隧洞左、右两侧洞壁出现岩体板裂现象。隧洞拱顶应变集中区范围缩小,左拱腰应变集中区范围增大,右下方竖向应变集中区范围增大,右拱腰上方应变集中区范围不变,应变集中区量值变化均很小。
7)t=3 094~3 462 s(轴向应力18.34~19.24 MPa)时,处于第5级加载过程,如图4(g)所示。裂纹1闭合,裂纹3、4、5无变化。裂纹3上端与洞口交汇处萌生1条沿左下方100°方向发展的剪切裂纹7,长度约3 cm;裂纹4右侧萌生新微小裂纹8,长度约2.5 cm; 裂纹6左下方、裂纹4与裂纹8附近岩体鼓起,并有小体积岩体开始剥落。隧洞发生严重脆性破坏,发出“砰”的声响。隧洞表面应变集中区范围无变化,每个应变集中区量值增大0.002左右。
综上,隧洞受荷过程中出现3种裂纹形式。1)初始裂纹: 加载过程中,隧洞周边拉应力集中区形成的张拉裂纹。2)远场裂纹: 隧洞洞周远端形成的裂纹,属于张-剪复合裂纹。3)剪切裂纹: 隧洞附近压应力集中形成的剪切裂纹。据此对隧洞表面出现的裂纹类型进行判别,裂纹1、2形成于裂纹萌生阶段,出现在隧洞拱顶、拱底位置,属于张拉裂纹;裂纹3、4、6、7受到压应力集中作用,萌生于隧洞两侧拱腰,属于剪切裂纹;裂纹5、8萌生于隧洞远端,属于远场裂纹。
2.2 表面应变场方差演化规律
隧洞受荷过程中,表面应变场出现的局部应变集中区是一种应变分异现象,而应变场方差可综合反映水平、垂直和剪切应变场的应变分量数据偏离其均值的程度,应变场方差越大,应变分异现象越明显[16]。
隧洞应变场方差计算步骤为: 导出水平、竖向及剪切应变场数据矩阵,由式(1)计算应变场方差矩阵,然后由式(2)计算应变场方差。
(1)
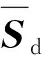
应变场方差
(2)
式中: |·|为矩阵行列式;p为张量维度,应变为二维张量,所以p=2。
隧洞变形过程应变场方差-轴向应变曲线如图5所示,表现出明显的阶段性变化。
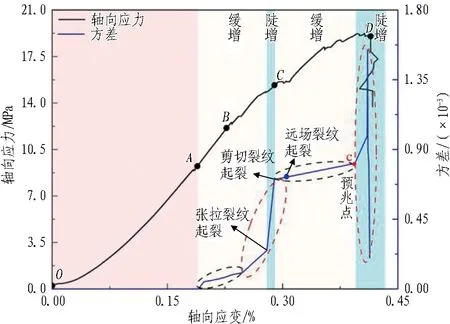
图5 隧洞表面应变场方差-轴向应变关系曲线
应变分量的方差矩阵
1)OA段(t=0~938 s,Fz=0~445 kN)。方差在0附近,隧洞处于内部微裂隙压密阶段,表面变形均匀,无应变集中区出现。
2)AB段(t=938~1 566 s,Fz=445~650 kN)。方差缓慢增加,隧洞拱顶和拱底出现应变集中区,表面应变场产生应变分异现象。
3)BC段(t=1 566~1 918 s,Fz=650~729 kN)。方差曲线由缓增转为陡增,隧洞拱顶及左拱腰出现应变集中区,拱底下方的应变集中区量值增大,故方差开始迅速增大。
4)CD段(t=1 918~3 462 s,Fz=729~962 kN)。方差呈现“缓增—陡增”的变化趋势,隧洞表面出现多个应变集中区,宏观上洞周远端出现远场裂纹。此后,隧洞表面应变集中区范围变化不明显,仅是应变数值不断增大。达到峰值荷载前隧洞表面裂纹开始不稳定发展,应变集中区贯通,形成大尺度的宏观裂纹,导致应变场分异程度陡增。
3 隧洞变形过程的声发射特征
3.1 声发射特征参数分析
岩体在变形过程中释放的声发射信号能反映岩体内部微裂纹的变化。图6和图7分别为隧洞加载过程中声发射振铃计数、幅值随时间变化曲线。
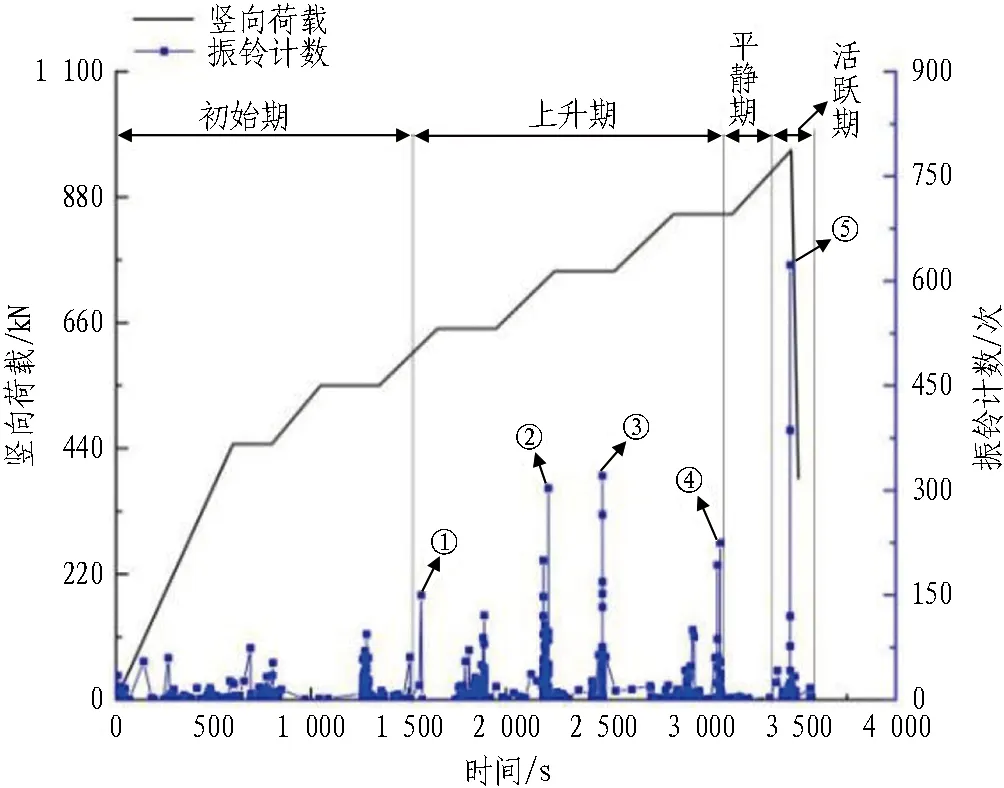
图6 声发射振铃计数-时间曲线

图7 声发射幅值-时间曲线
1)初始期(t=0~1 500 s,Fz<645 kN)。0~1 500 s时为加载初期,岩体内部微裂纹闭合产生了一些较弱的声发射事件,振铃计数在0~90次、幅值在0~59 dB波动。
2)上升期(t=1 500~3 100 s,Fz=645~920 kN)。t=1 500~1 566 s(Fz=645~650 kN)时,振铃计数和幅值出现第1次跃升(图中标注①),跃升时振铃计数为150次、幅值为63 dB,隧洞出现张拉裂纹1、张拉裂纹2(见图4(b))。t=1 566~2 218 s(Fz=650~780 kN)时,振铃计数和幅值出现第2次跃升(图中标注②),振铃计数达到200次、幅值为65 dB,隧洞萌生剪切裂纹3、远场裂纹4,左侧洞壁岩体剥落(见图4(d))。t=2 218~2 487 s(Fz=780~805 kN)时,振铃计数和幅值出现第3次跃升(图中标注③),跃升时振铃计数为321次、幅值为75 dB,隧洞萌生新的远场裂纹5,右侧洞壁岩体发生剥落(见图4(e))。t=2 487~3 094 s(Fz=805~917 kN)时,振铃计数和幅值出现第4次跃升(图中标注④),跃升时振铃计数为225次、幅值为70 dB,隧洞左侧洞壁出现新的剪切裂纹6(见图4(f))。
3)平静期(t=3 100~3 400 s,Fz=920~953 kN)。声发射活动进入平静期,振铃计数稳定在0次附近,幅值在32 dB左右波动,隧洞表面宏观裂纹无明显变化。
4)活跃期(t=3 400~3 500 s,Fz=953~762 kN)。振铃计数和幅值快速增至最大值,振铃计数623次、幅值90 dB,裂纹之间相互贯通,隧洞表面出现多条长裂纹(见图4(g))。
3.2 声发射b值特征
声发射b值(裂纹扩展尺度的函数)变化能够反映岩石内部微裂纹尺度的演化。b值增大,声发射小事件所占比例增加,以小尺度微破裂为主;b值不变,大小事件的分布不变,不同尺度的微破裂状态比较稳定;b值减小,大事件的比例增加,大尺度的破裂增多[17]。
采用最小二乘法计算b值,见式(3)。计算过程中,选取震级分档间距Δm=0.5,每100个声发射事件为1组数据,以50个事件为滑动窗口,得到隧洞变形全过程的声发射b值变化曲线如图8所示。
(3)
式中:Mi为第i档声发射事件的中数;Ni为第i时间段的声发射频度。
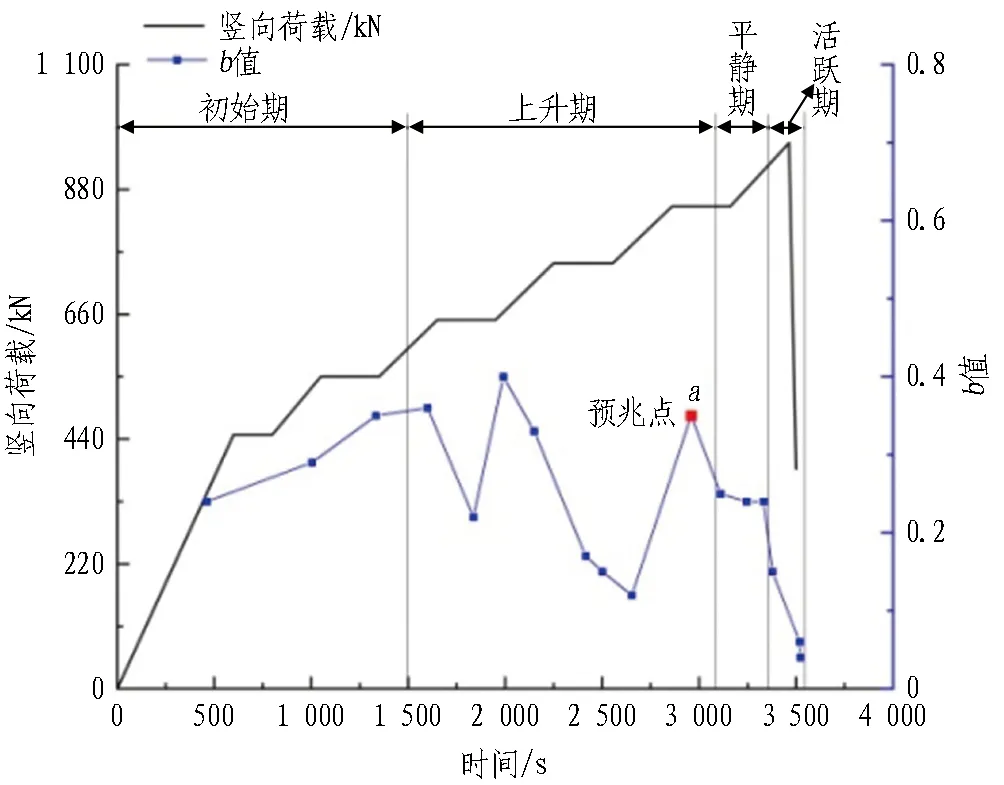
图8 声发射b值随时间变化曲线
初始期,声发射b值由0.24缓慢增加至0.35,隧洞内部的孔隙和微裂纹闭合。上升期,b值在0.12~0.4波动明显,声发射大小所占比例处于不停变化中,说明隧洞尺度不一的初始裂纹和新生裂纹发展不稳定。平静期,b值由0.35下降至0.25后趋于平稳,大事件比例稍有增加;随后,大小声发射事件分布不变,隧洞表面裂纹不再扩展。活跃期,临近峰值荷载时,b值大幅下降至0.04,声发射大事件所占比例增大,内部裂纹迅速扩展,相互贯通为更大的裂纹,隧洞发生脆性破坏。
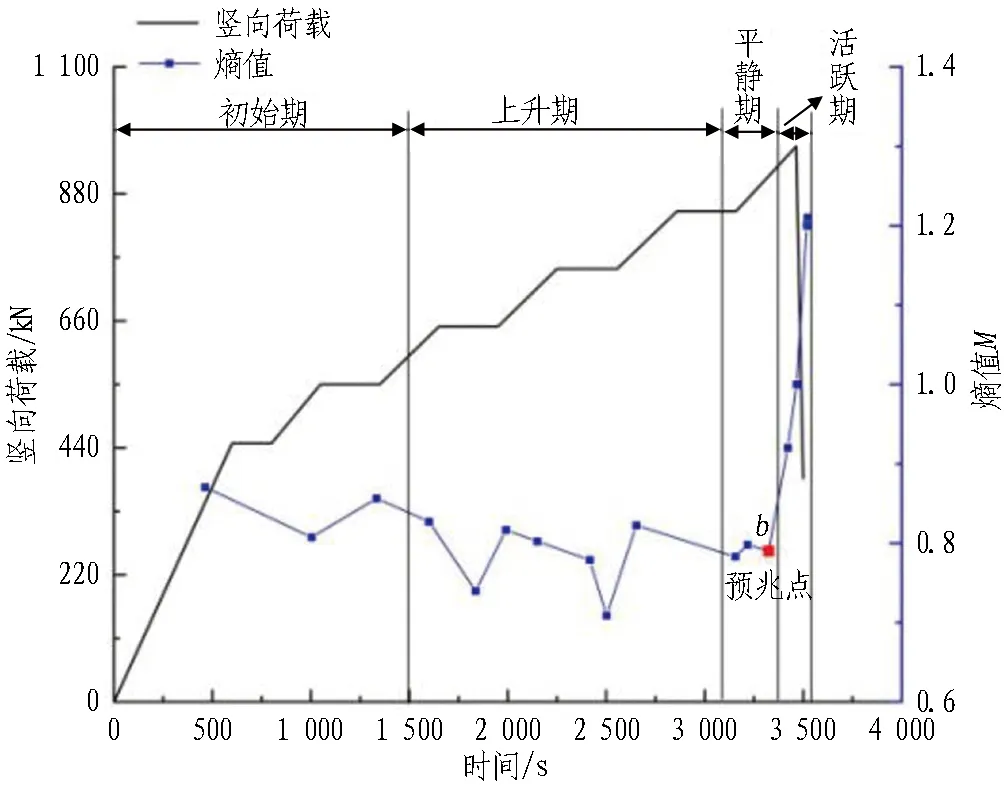
3.3 声发射熵值特征
声发射熵值能够反映隧洞变形过程中声发射事件的变化及能量的耗散[18]。试验获得的声发射信号是一个离散的样本空间X={xi},其中i=1,2,3,…,n,(n∈N)。每种信号出现的概率可表示为Pi=P(xi),且有:
(4)
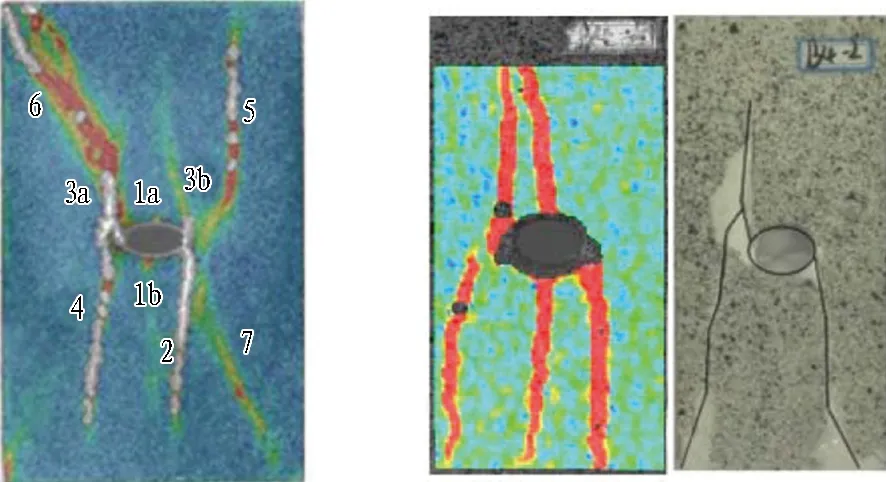
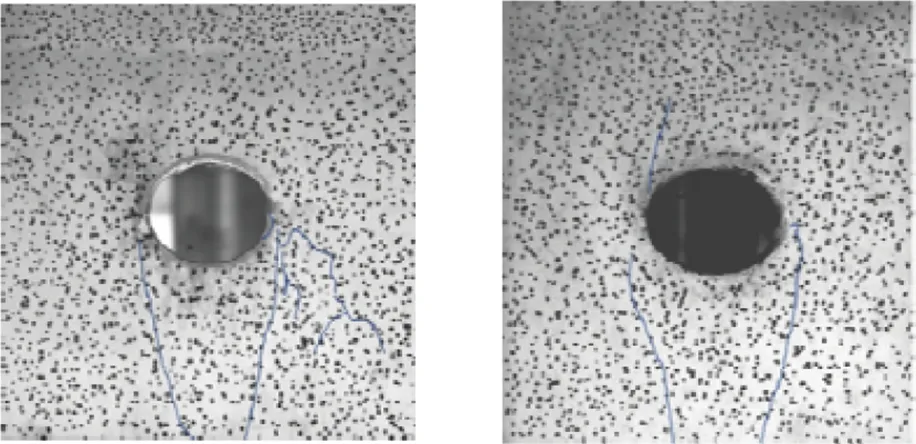
式中0 在时间序列上定义一个时间窗口,以窗口末尾时间作为计算熵值的时刻。设初始窗口宽为w∈N,窗口的移动因子σ∈N,则第m个滑动窗口内声发射事件数取值状态出现的概率 (5) 由式(4)、(5)得出第m个滑动窗口对应的累计熵值 (6) 式中:M(i)为归一化熵值;k为常数,k=1/log(i)(k≥0)。 编制Matlab程序计算声发射熵值。每100个声发射事件数为滑动窗口,得到隧洞变形全过程的声发射熵值变化如图9所示。 图9 声发射熵值随时间变化曲线 初始期和上升期,熵值在0.7~0.87波动,表明声发射事件少、能量小,隧洞裂纹渐进式扩展; 平静期,熵值保持在0.8附近,表明声发射事件不变,隧洞裂纹不发生变化; 活跃期,熵值瞬时突增至最大值1.21,表明声发射事件大量产生,能量突增,小裂纹扩展形成大尺寸裂纹,隧洞发生破坏。 分形维数广泛用于描述岩体破裂面的形貌特征,采用盒维数法[19]计算图像分形维数,公式为: (7) 式中:D为分形维数;Nr(A)为用于测量分形结构大小的函数;r为盒子的尺寸。 将高速摄像机获得的数字图像裁剪成相同尺寸的图像,通过Matlab编程实现隧洞宏观裂纹图像的读取和二值化处理,将得到的裂纹RGB图像转化为灰度图像。为避免隧洞空洞对图像采集的影响,图像处理时首先提取岩体的颜色对隧洞区域进行填充,然后计算其分形维数(见图10)。 图10 隧洞表面裂纹的分形维数-时间关系 隧洞裂纹扩展过程的分形维数变化可分为3个阶段。1)线性阶段(Ⅰ)。隧洞处于弹性变形阶段,无肉眼可见的裂纹出现(见图4(a)),分形维数维持在0附近。2)裂纹稳定扩展阶段(Ⅱ)。隧洞拱顶及拱底萌生张拉裂纹(见图4(b)),分形维数快速增至1.11(K1点);随后,隧洞左拱腰出现剪切裂纹(见图4(c)),裂纹分形维数增长速率加快,增至1.34(K2点);隧洞远端萌生远场裂纹后(见图4(d)),裂纹分形维数增至1.43(K3点);裂纹逐步扩展,分形维数发生突增,由1.58增至1.72(d点),分形维数曲线斜率增长至最大值约为0.001 2,此时隧洞表面出现新的微小裂纹且发生岩体剥落,破坏区域增大。3)峰后跌落阶段(Ⅲ)。隧洞发生破坏,裂纹基本不再扩展,分形维数维持在1.81附近保持不变。 因此,分形维数接近于0时,裂纹所在区域是隧洞表面离散分布的一些小区域;分形维数接近1.1时,表明裂纹所在区域趋向于沿隧洞表面内的直线分布;分形维数接近于2时,表明裂纹所在区域趋向于整个隧洞表面分布,隧洞即将破坏。 不同预警参数对应的隧洞破坏预警时间不同,预警时间为2 829~3 283 s,预警荷载为峰值荷载的87%~97%,见表1。应变场方差陡增预警时间为3 283 s,对应峰值荷载的97%(见图5)。声发射平静期预警时间为3 119 s,对应峰值荷载的88%,持续时长246 s(见图6)。声发射b值大幅下降预警时间为2 829 s,对应峰值荷载的87%(见图8)。声发射熵值陡增预警时间为3 240 s,对应峰值荷载的92%(见图9)。裂纹分形维数突增预警时间为2 966 s,对应峰值荷载的87%(见图10)。声发射b值预警时间最早,应变场方差预警时间最晚,二者相差454 s。实验室条件下得出试验结果的预警时间是有局限性的,但同时能给隧洞工程一个参考,预判隧洞破坏时间。 表1 不同参数对应的隧洞破坏预警时间统计表 隧洞表面裂纹的扩展过程表明,隧洞短轴上下方首先出现沿竖向加载方向延伸的应变局部化区域,说明隧洞的拱顶和拱底先出现拉应力。当拉应力超过砂岩的抗拉强度时,隧洞拱顶及拱底首先出现张拉裂纹,且张拉裂纹沿着与轴向应力平行的方向稳定扩展。随着荷载的增大,隧洞两侧曲率半径最小的拱腰位置出现压应力集中,当压应力集中大于岩体抗剪强度时,剪切裂纹扩展、切割岩体,围岩发生剥落,隧洞拱腰处发生板裂状破坏,形成V形槽。洞周裂纹逐步扩展,隧洞内部应力不断调整,在隧洞两侧萌生远场裂纹。此时,随着与洞周边界距离的增加,拱底和拱顶的拉应力逐渐减小,张拉裂纹扩展至拉应力为0的位置后便停止发展。然而,受远场裂纹发展的侧向压缩作用影响,张拉裂纹会逐渐闭合。最终,隧洞两侧远场裂纹向顶、底部及V形槽扩展,使得隧洞发生脆性破坏。 学者对含椭圆形孔洞真实岩体的破坏进行了研究,Li等[20]对含不同倾向椭圆形孔洞的棱柱状大理岩试样进行单轴压缩试验,发现孔洞正上、正下方首先萌生2条张拉裂纹并沿加载方向扩展,随着孔洞左右侧剪切裂纹的萌生与扩展,2条拉伸裂纹逐渐闭合(见图11(a))。李尧[21]进行了椭圆孔洞大理岩单轴压缩试验,发现隧洞破坏模式为孔洞左右两端萌生向下端扩展的拉伸-剪切混合型裂纹,左端出现向上端扩展的拉伸裂纹(见图11(b))。张栩栩[22]开展了类岩石材料含椭圆形孔洞试样的单轴压缩试验,发现孔洞上、下部短轴端点首先萌生沿主应力方向扩展的拉伸裂纹,最终试样长轴端点或远端产生剪切裂纹,与孔洞贯通形成宏观破坏面(见图11(c))。与本文砂岩隧洞破坏形态相比(见图11(d)),横置椭圆形隧洞的破坏均是先出现张拉裂纹,随后出现剪切破坏;而本文砂岩隧洞并未形成大的剪切破坏面,围压抑制了张拉作用,压剪作用逐渐增强,最终表现出拉-剪混合破坏。 (a) 大理岩[20] (b) 大理岩[21] (c) 类岩石[22] (d) 本文砂岩隧洞 本文开展的相同试验条件下另2个椭圆形隧洞的破坏形态如图12所示。 (a) 模型2 (b) 模型3 对比3个模型的破坏形态,相同点为: 隧洞破坏形态不对称,破坏时左右两侧拱腰裂纹都沿主应力方向发展至隧洞底部。不同点为: 模型1右侧拱腰衍生1条拉-剪复合裂纹发展至洞顶,隧洞左下方和右上方表面岩体鼓起;模型2在右侧拱腰下方表面岩体轻微鼓起;模型3表面无岩体鼓起,但左侧拱腰出现1条沿70°向右上方发展的拉-剪复合裂纹。因此,尽管椭圆形隧洞的形状、边界条件、外荷载都对称,但由于岩体的非均匀性,隧洞宏观裂纹的发展和破坏形态并不对称。 1)隧洞受荷载过程中,拱顶和拱底先出现张拉裂纹,随后左侧拱腰出现剪切裂纹,隧洞右上方和右下方出现远场裂纹,伴随表面岩体剥落。隧洞两侧的远场裂纹最终扩展至顶部和底部,并与拱腰裂纹贯通,最终导致隧洞发生脆性破坏。隧洞表面应变场呈现明显的局部化应变特征,应变集中区先于宏观裂纹出现,最终形成覆盖裂纹扩展路径的应变集中区。 2)隧洞变形过程中,声发射振铃计数和幅值变化趋势具有一致性。第1次跃升,对应已有裂纹扩展和新裂纹萌生;第2~4次跃升,对应大尺寸裂纹出现及表面岩体鼓起、剥落;经历一段平静期后,声发射振铃计数和幅值再次跃升至各自峰值,隧洞发生破坏。 3)隧洞表面裂纹的分形维数与裂纹萌生、扩展过程紧密相关。当分形维数达到1.1时,隧洞表面出现宏观裂纹;当分形维数大于1.8且趋于稳定时,隧洞发生完全破坏。 4)隧洞破坏前会出现声发射平静期、b值突降、熵值突增、应变场方差突增、裂纹分形维数突增等前兆信息。不同物理场监测数据的预警时间不同步,预警时间为3 119~3 283 s,预警荷载为峰值荷载的87%~97%。其中,声发射b值预警时间最早,应变场方差预警时间最晚。 试验过程中数据的采集方法及采集精准程度有待进一步研究;此外,由于实际隧洞工程岩体的非均质性及破坏的复杂性,实际应用时应将声发射信号的平静期和熵值2个参数相结合作为岩体破坏的前兆特征。下一步拟对模型试验中预警部分的引用进行深化研究,编程开发一个可供工程应用的预警系统。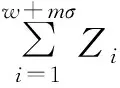
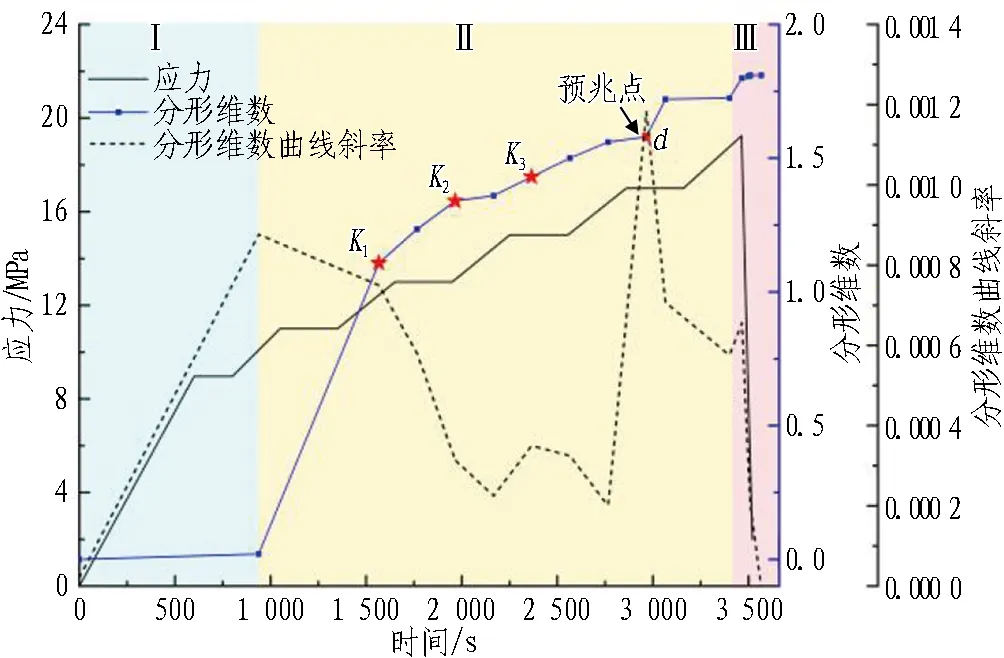
4 隧洞表面宏观裂纹扩展的分形表征
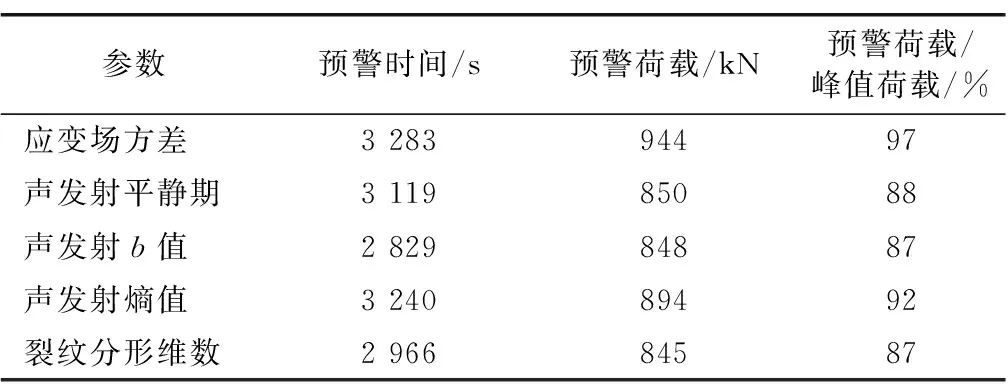
5 隧洞破坏预兆及破坏特征
5.1 不同参数的破坏预警时间
5.2 裂纹扩展机制分析
5.3 隧洞破坏形态对比

6 结论与讨论
