寒区隧道冻结特性及冻结深度预测
2023-09-15黎忠灏邱军领赖金星罗燕平冯志华
马 超, 黎忠灏, 邱军领, *, 赖金星, 罗燕平, 曾 斌, 冯志华
(1. 长安大学公路学院, 陕西 西安 710064; 2. 四川川交路桥有限责任公司, 四川 广汉 618300; 3. 河北省交通规划设计研究院有限公司, 河北 石家庄 050011)
0 引言
随着我国交通运输行业的快速发展,隧道工程建设逐步向高海拔、高纬度地区发展,所面临的环境、气候等工程地质条件越来越复杂。在季节性冻土区,隧道施工和运营遇到了一系列严重的冻融病害。截至2018年底,我国共有15 117座铁路隧道。其中,发生冻害的铁路隧道有7 921座,占铁路隧道总数的52.4%;发生严重冻害的铁路隧道有3 855座,占铁路隧道总数的25.5%。我国发生冻害的隧道主要集中于高纬度和高海拔地区,分布于青藏高原、东北和内蒙古等地区。寒区隧道冻害的发生与温度场和围岩的冻结深度有关。围岩的最大冻结深度是影响冻胀力的重要因素,同时也是防排水设施埋设深度的重要依据[1]。
夏才初等[1]以准稳态假设为基础,利用积分方法推导了在考虑衬砌、保温层和冻结围岩中未冻水含量情况下的最大冻结深度解析表达式。张晨曦等[2]对20座隧道的温度场进行了数值模拟,结果表明,随着地表温度和洞外气温的上升,隧道的径向冻结深度逐渐减小。丁云飞等[3]通过数值仿真得出隧道入口段冻结深度与冻结时间和外界温度密切相关的结论,冻结时间越长冻结深度越大,在极端气温下洞口冻结深度可达到8.2 m。王建军等[4]对竖井施工过程中的温度变化进行了现场监测,得出竖井冻结深度的主要影响因素是通风时间,而风速对竖井冻结深度的影响不大。周元辅等[5]通过室内试验对冻结深度的不同计算方法进行分析,发现采用鲁基扬诺夫公式计算冻结深度比其他方法更加精确。赵鑫等[6-7]对兴安岭隧道进行了温度实测,研究了温度场的时空分布特征,并基于斯蒂芬法建立了冻结深度的计算方程。随着计算机技术的飞速发展,机器学习方法已经应用到各行各业中[8-9]。一些学者将机器学习引入到隧道工程的施工与运营中。例如: 王冰泉等[10]利用集成模拟策略训练了基准时期的支持向量机模型,用于模拟过去和未来季节冻土的最大冻结深度。
上述对寒区隧道冻结深度特性的研究,主要关注的是冻结深度与温度、时间的关系,而对冻结深度沿隧道径向及环向的变化规律及影响因素研究较少。针对冻结深度的预测问题,学者们多采用现场试验与理论推导相结合的方法,而采用机器学习方法的研究较少。本文对冻结深度沿隧道径向及环向的变化规律以及冻结深度各影响因素的显著性及敏感性进行探究,并提出一种基于XGBoost(extreme gradient boosting)和LightGBM(light gradient boosting machine)的混合模型对冻结深度进行预测,以期为寒区隧道防冻害研究及设计提供参考。
1 工程背景
兴安岭隧道是内蒙古最寒冷地区呼伦贝尔市牙克石和阿荣旗交界处的一条重要公路隧道,其横穿大兴安岭中南部的中、低洼山区。该地区最高海拔为1 210 m,山势总体平缓。由于地处欧亚高纬度地区,该地区春季干燥风大,夏季温凉短促,秋季气温聚降,冬季寒冷漫长。山区积雪深厚,部分地区霜冻深度超过3 m。历年最低气温为-46.7 ℃,最大风速为29 m/s。隧道为双向4车道,最高设计时速为100 km,左线隧道里程为ZK164+605~ZK168+565,全长3 960 m,交通方向由牙克石到阿荣旗。
2 温度场及冻结深度特性分析
2.1 数值模型建立
采用有限元软件ANSYS建立洞口段温度场,得出衬砌及围岩中温度场的分布情况。隧道受环境影响的最大深度为20 m[11],因此所建立的模型上下边界、左右边界均距隧道衬砌20 m。模型的对称面、恒温边界及对流换热边界如图1所示。其中,为了清晰地显示对流换热边界,将二维平面图进行了旋转。
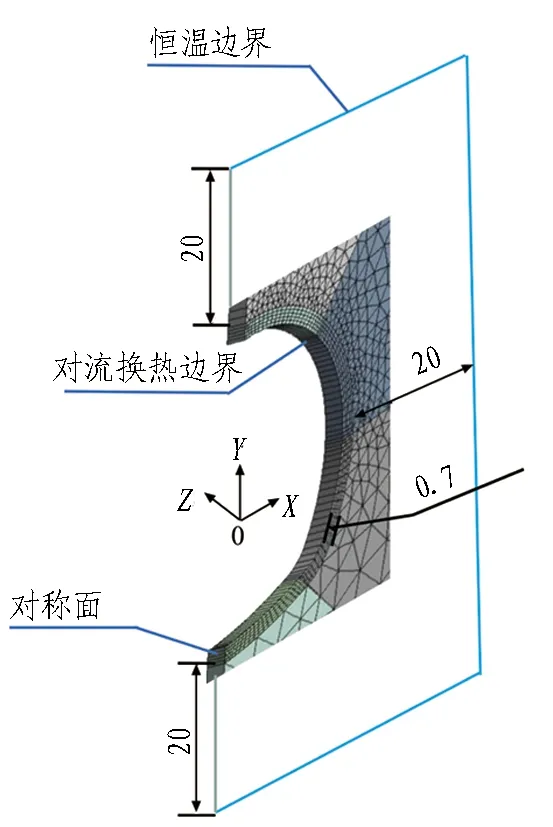
图1 计算模型(单位: m)
空气与衬砌之间的对流换热系数取10 W/(m2·k)[12-13]。洞内沿程的温度荷载根据兴安岭隧道各断面壁面温度的监测数据确定,即将兴安岭隧道现场实测数据进行函数拟合,然后将所拟合的函数作为温度荷载施加于隧道衬砌表面。考虑到数值模拟的结果主要用于定性研究,研究中并未具体到某一天,且为了方便建模并简化计算,温度荷载加载的时间均取360 d,加载步长均取1 d。模型的初始温度是围岩的初始地温,综合考虑当地气温条件并参考文献[14-15],取兴安岭隧道全年实测温度值的平均值并取整作为初始温度,则得到模型的初始温度为3.5 ℃。结合兴安岭隧道的相关资料及文献资料[9-10],模型的热力学参数如表1所示。

表1 模型的热力学参数
2.2 数值模型合理性验证
为验证数值模型的合理性,提取各断面径深1 m处的温度数值模拟结果与实测数据进行对比,如图2所示。

图2 各断面径深1 m处的温度数值模拟结果与实测数据对比
通过图2可知,温度模拟结果与实测数据变化规律一致且变化曲线基本吻合。实测数据与数值模拟结果最大差值为1.51 ℃,平均差值为0.42 ℃,满足工程中对数值模拟计算的误差要求[3]。
2.3 数值模拟结果分析
2.3.1 温度场分布规律
为进一步分析隧道围岩径向的温度场分布规律,建立仰拱中心沿隧道径向的求解路径,提取数值模拟结果,并将各断面径向的温度模拟结果绘制成如图3所示的点线图。

(a) 距洞口50 m
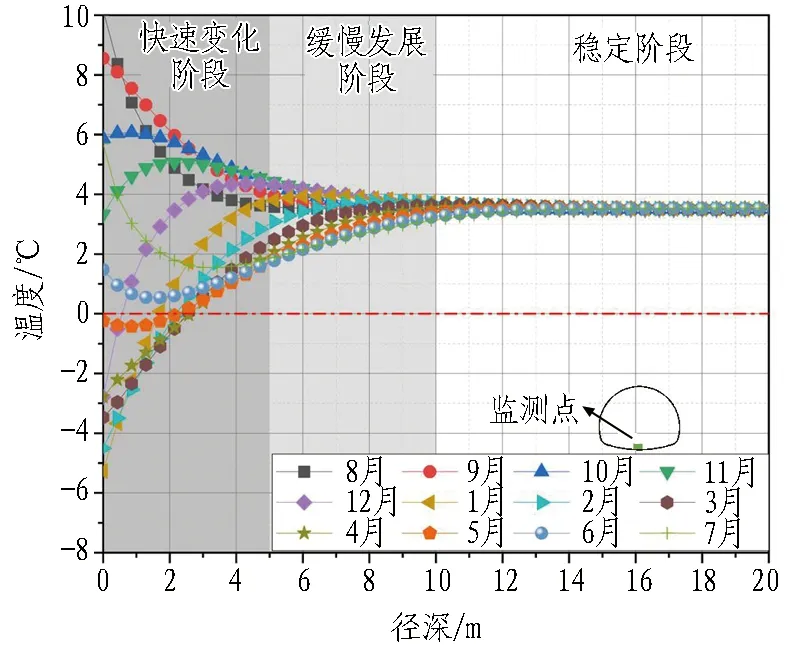
(b) 距洞口150 m

(c) 距洞口300 m
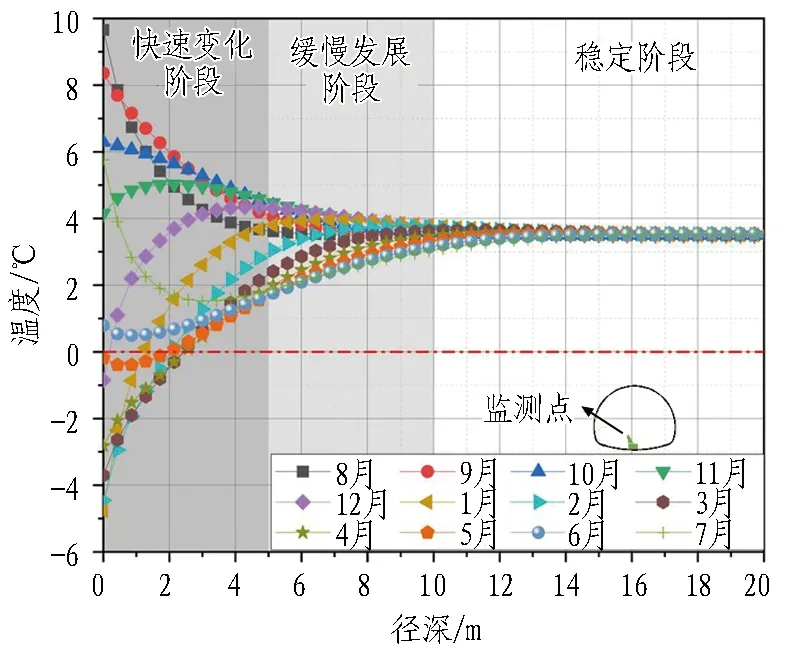
(d) 距洞口500 m
由图3可以看出:
1)各个断面沿径向的温度场分布规律与洞内气温紧密相关。对于气温高于初始地温的8、9、10月,围岩径向温度逐渐减小;对于气温低于初始地温的1、2、3、4、5月,围岩径向温度逐渐增加。但最终都趋于稳定,稳定后的围岩温度值与初始地温相近。11月出现了反常的先增后减现象,6月、7月出现了反常的先减后增现象。这主要是由于6月、7月、11月处于正负温交替时期,而围岩中热量的传递具有一定的滞后性,6月、7月、11月受到围岩中原赋存热量的影响出现了反常的先增后减或先减后增现象。
2)根据各断面围岩不同径深温度场的变化情况,并综合考虑温度场的变化对隧道的影响程度[2-3],可将围岩温度沿径向的变化划分为快速变化阶段、缓慢发展阶段、稳定阶段3个阶段。不同阶段划分的主要依据是围岩温度沿径向的变化幅度。当每米范围内围岩温度的变化幅度超过0.5 ℃时,将其界定为快速变化阶段;当每米范围内围岩温度的变化幅度在0.1~0.5 ℃时,将其界定为缓慢发展阶段;当每米范围内围岩温度的变化幅度小于0.1 ℃时,将其界定为稳定阶段。则快速变化阶段的范围是沿径深0~5 m,缓慢发展阶段的范围是沿径深5~10 m,在沿径深10 m之后,围岩温度稳定在初始地温附近,这也表明了隧道内气温对围岩温度场的最大影响范围为10 m。
2.3.2 冻结深度分布规律
在不考虑隧道进出口高程差、隧道内交通量以及车辆行驶速度的情况下,并以0 ℃作为围岩是否发生冻结的判断依据,各断面不同位置冻结深度变化规律如图4所示。

图4 各断面不同位置冻结深度变化规律(单位: m)
由图4可知: 1)距洞口50、150、300、500 m处的最大冻结深度分别为3.99、2.61、2.42、2.35 m,相比于前一断面,各断面最大冻结深度降幅分别为34.6%、7.3%及2.9%。这表明距洞口越远围岩冻结深度越小,距洞口越近围岩冻结深度变化越大,在距洞口300 m之后冻结深度趋于稳定。2)各个断面不同部位冻结深度的变化规律基本一致。除仰拱部位冻结深度明显较大外,其余各部位未出现明显差别。这主要是由于仰拱部位相较于其他部位地下水含量高,围岩中赋存孔隙水多;此外,地下水的流动会带走热量,促进围岩的冻结。
3 冻结深度影响因素分析
3.1 正交试验及影响因素确定
冻结深度受初始地温、最冷月平均气温、衬砌和围岩热力学参数(热导率、比热容)等诸多因素的影响。为了探讨影响冻结深度各种因素的显著性、敏感性及其与冻结深度的关系,采用ANSYS软件并结合正交试验方法进行分析。
正交试验本质上是一种局部试验,在试验中找到一组有代表性的点作为试验对象,通过正交试验可以减少试验次数,降低工作量[16]。本次试验研究的影响因素包括最冷月平均气温﹑初始地温、衬砌导热系数、围岩导热系数、衬砌比热容、围岩比热容,每个因素设计5个水平。衬砌导热系数、围岩导热系数、衬砌比热容及围岩比热容以表1中的数据为基准参数,最冷月平均气温取距洞口50 m断面处的监测结果,并在此基础上对各参数分别增15%、30%和减15%、30%作为试验的5个试验水平,具体取值如表2所示。本试验是以6因素5水平为标准进行正交试验的,因此选择L50(511)正交表进行试验,共需进行50次试验。
3.2 试验结果分析
3.2.1 各影响因素敏感性与显著性分析
正交试验分析一般采用方差分析法或直观分析法。直观分析法计算简单,但无法给出各因素的显著性;方差分析法比较精细,计算量稍大,但可以根据方差分析结果给出各因素的敏感性及显著性。因此,本文采用方差分析法进行分析。
方差分析主要包括计算离差平方和、计算自由度、计算平均离差平方F和显著性检验4步[17]。F值越大表明该因素对试验结果的影响越敏感。给定显著性水平0.005,若F>F0.005(fi,fE)=F0.005(f4,f19),则该因素对结果影响显著。其中,fi为因素自由度,fE为误差自由度。

表2 影响因素参数取值
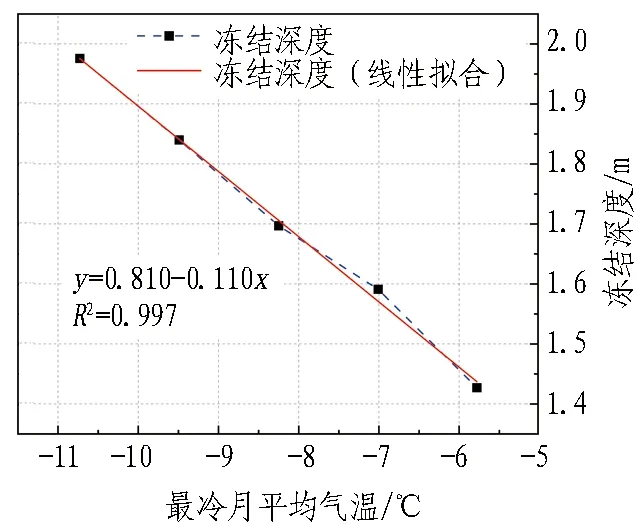
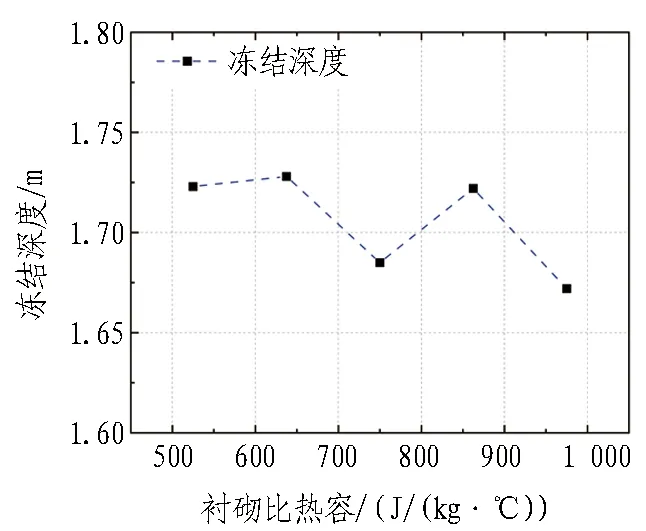
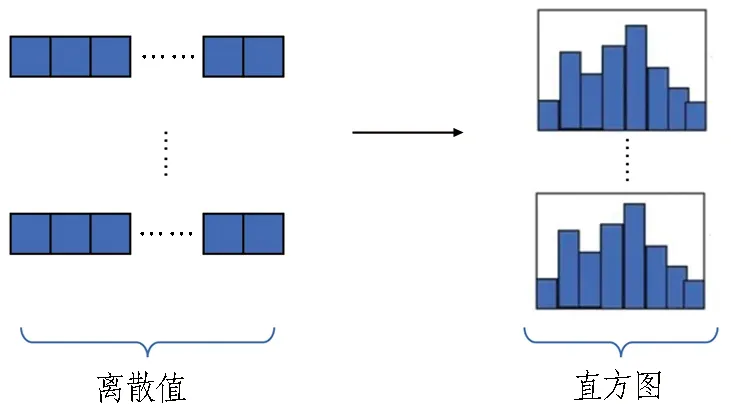
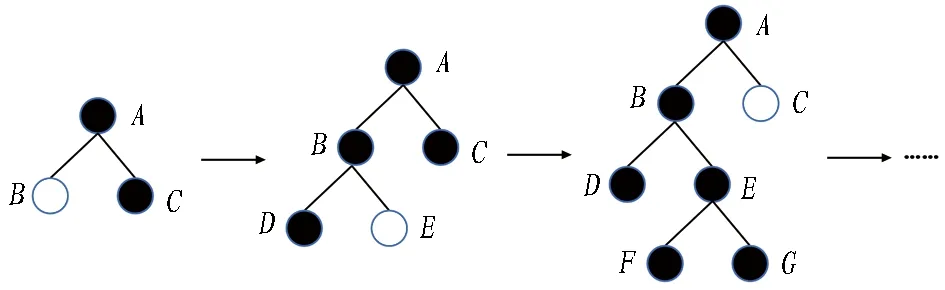
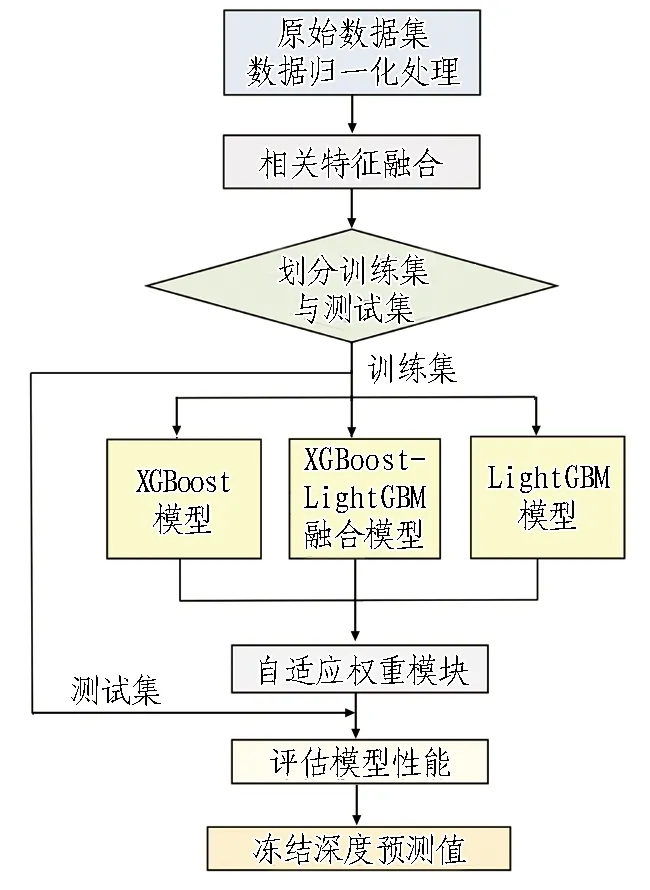
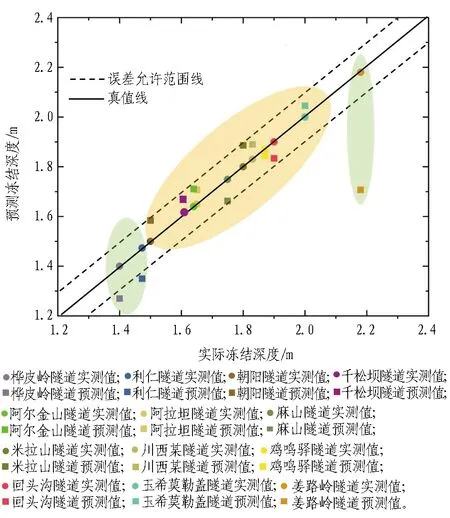
经过方差分析之后的试验结果如图5所示。从图中F值的大小可以看出,不同因素对冻结深度的影响从大到小排序为: 初始地温>最冷月平均气温>围岩比热容>围岩导热系数>衬砌导热系数>衬砌比热容。在显著性水平为0.005的条件下,F(A)=345.602>F0.005(4,19)=5.27;F(B)=393.229>F0.005(4,19)=5.27;F(C)=86.119>F0.005(4,19)=5.27;F(D)=207.918>F0.005(4,19)=5.27;F(E)=35.181>F0.005(4,19)=5.27;F(F)=4.644 3.2.2 各影响因素与冻结深度之间的变化关系分析 根据所确定的影响因素以及相应的试验水平,选用L50(511)正交表进行试验,试验次数共计50次。在得到试验结果之后,求出各影响因素估算边际平均值,以各因素的实际水平作为横坐标,以冻结深度作为纵坐标,绘制各影响因素与冻结深度间的变化关系曲线图,结果如图6所示。 图5 各影响因素F值 (a) 最冷月平均气温 (b) 初始地温 (c) 围岩导热系数 (d) 围岩比热容 (e) 衬砌导热系数 (f) 衬砌比热容 从图6中可以看出: 1)冻结深度与衬砌导热系数、围岩导热系数呈线性正相关,冻结深度随着这2种因素的增大而逐渐增大; 2)冻结深度与最冷月平均气温、初始地温和围岩比热容呈线性负相关,冻结深度随着这3种因素的增大而逐渐减小; 3)冻结深度与衬砌比热容并未呈现出明显的线性关系,且各水平之间的冻结深度最大差值仅为0.056 m,说明衬砌比热容的变化对冻结深度影响不显著。 由于冻结深度受多种因素综合影响,且现场监测费用高、难度大,难以直接测得,常采用理论分析、经验回归公式进行预测。随着计算机技术的不断发展,对冻结深度的预测不再局限于统计回归方法,而是采用SVR、XGBoost、MLP、LGBM等大数据算法进行预测。本节提出了一种基于权重分配组合模型的冻结深度预测方法。 4.1.1 XGBoost预测模型 XGBoost算法是一种设计良好的梯度增强决策树(gradient boosting decision tree,GBDT)算法。该方法在对数据进行逐个构造的基础上,逐步积累和综合多个弱学习器,从而获得较好的回归和分类性能,其计算流程如图7所示。XGBoost算法运算速度快、训练效果较好,且可以有效避免过度拟合[18]。 图7 XGBoost算法流程图 XGBoost算法预测函数如下: (1) 式中:yi为整个模型在这个样本上的预测结果;k为弱评估器的总数量;fk为第k棵决策树;xi为样本i对应的特征向量。 XGBoost的目标函数由2部分组成: 一是模型误差,即样本真实值和预测值之间的差值;二是模型的结构误差,即正则项,用于限制模型的复杂度[19-20]。目标函数 (2) (3) 为了使得目标函数O(θ)最小,对损失函数部分进行二阶泰勒展开,并求导使其为0,得到每个节点的最优预测值为 (4) 式中:ωj为第t棵树的叶节点j对应的最优预测值;Gj和Hj分别为所有样本在ft的j节点上gi与hi的和。 将式(4)代入目标函数(最优评分函数)得 (5) XGBoost模型可以选择信息增益最大的节点分裂,假设分裂前的节点为j,该节点分裂为左子节点L和右子节点R,对目标函数(最优评分函数)的贡献为: (6) (7) 节点j分裂前的目标函数(最优评分函数)的贡献和为: (8) 因此,节点j分裂后的信息增益为: Gain=O(R+L)-O(R)-O(L)。 (9) 式中Gain为分裂前损失与分裂后损失的差值,差值越大,代表分裂后的损失越小。 XGBoost计算Gain时遍历所有特征所有可能的分割点,选取Gain值最大的节点进行分割。该方法的优点是精度高,但计算量太大。 4.1.2 LightGBM预测模型 LightGBM是GBDT算法的一种实现方法,该算法将Leaf-wise算法和直方图算法相结合,使其训练速度快、内存消耗小、准确率高,且支持分布式处理大量的数据。LightGBM计算流程如图8所示[21]。 4.1.2.1 直方图算法 首先,对连续的浮点特征值进行离散,得到K个分段函数,并构造宽度为K的直方图;然后,通过对各分块进行迭代,得到各分块在直方图上的累计统计量。在进行特征选取时,仅需从直方图上求取最佳分割点即可。因此,直方图算法具有节约储存空间、提高计算效率等优点[22]。直方图算法如图9所示。 图8 LightGBM计算流程[21] 图9 直方图算法 4.1.2.2 带深度限制的Leaf-wise算法 LightGBM在分裂过程中采取了Leaf-wise生长策略,每一次选择1片具有最大分裂能力的叶片进行分裂,具体分裂过程如图10所示。○代表最佳分裂节点,第1次分裂以节点B作为最佳分裂节点进行分裂,第2次分裂遍历节点D、E、C后以节点E作为最佳分裂节点进行分裂。在分裂次数相同的情况下,Leaf-wise可以降低误差,精度较高,且LightGBM会在Leaf-wise的基础上增加一个最大深度的限制,在保证高效率的同时防止过度拟合[23]。 图10 带深度限制的Leaf-wise分裂过程 4.2.1 模型混合方式 XGBoost预测模型具有兼容中小型数据集、处理缺失值的内置函数、可以在每次迭代后运行交叉验证等优点;LightGBM预测模型具有更快的训练速度和更高的效率,可降低内存使用率,比其他增强算法具有更高的准确性。为了将2种模型的优势相结合,提出了一种混合模型算法。该混合模型算法的具体步骤是: 1)利用XGBoost模型对冻结深度进行预测得到ya; 2)利用LightGBM模型对冻结深度进行预测得到yb; 3)将XGBoost模型和LightGBM模型进行融合,利用融合模型Hyb对冻结深度进行预测得到yc; 4)自适应权重部分,通过批量梯度下降法迭代训练模型权重α、β、γ; 5)将4)中得到的权重α、β、γ分别分配给混合模型中的单模型预测值ya、yb、yc,并通过线性公式y=αya+βyb+γyc得到最终预测值y。 4.2.2 数据归一化与反归一化 由于数据特征因素之间的基本单位不同,需要进行归一化处理,通过离差标准化将不同特征统一取值为0~1,计算公式为: (10) 得到预测结果后再通过反归一化还原为原本的量纲,其计算公式为: y=xa(xmax-xmin)+xmin。 (11) 式(10)—(11)中:xb为原始数据;xa为归一化后的量纲为1的数据;xmax为x的最大值;xmin为x的最小值;y为反归一化后的数据。 4.2.3 模型评估方法 为了评估各模型的预测精度,衡量预测值与真实值之间的偏差,采用平均绝对百分比误差(MAPE)、平方相关系数(R2)以及均方根误差(RMSE)对模型的可靠性进行评估,其计算公式分别为: (12) (13) (14) 由式(12)—(14)可看出,MAPE值越小模型的预测准确度越高;R2越接近于1,模型的拟合效果越好;RMSE越小模型离散度越低。 4.2.4 预测模型结构 冻结深度预测模型预测流程如图11所示。计算特征选取对冻结深度影响显著的初始地温、最冷月平均气温、围岩比热容、围岩导热系数及衬砌导热系数。相关特征融合是指将可能存在交互作用的特征进行融合,并作为新的特征参与训练,例如: 最冷月平均气温与初始地温均为环境特征,将最冷月平均气温与初始地温进行融合形成最冷月平均气温×初始地温特征参与训练。 图11 冻结深度预测模型预测流程 机器学习将数据集划分为训练集与测试集,训练集用于学习,测试集用于检验预测效果。训练集与测试集的数据来源于第3章正交试验所获取的50组试验数据。考虑到机器学习需要的数据量较大,在此基础上又进行了50次试验,总计100组数据。正交试验与所补充的50次试验地温、围岩热力学条件等参数是不相同的,以保证基础数据的多样性。训练集与测试集按照7∶3的比例进行划分,即训练集为70组数据,测试集为30组数据。评估模型采用的指标为4.2.3节所述的MAPE、R2以及RMSE。 XGB(XGBoost)、LGB(LightGBM)、Hyb及其混合模型预测结果如图12所示。由图可以看出: 与真实冻结深度值相比,XGB、LGB以及Hyb均有较好的预测结果,变化趋势一致性较高;而LGB+XGB+Hyb模拟结果相较于其他模型来说更加稳定,拟合程度更高,几乎与真实的冻结深度值重合。 各模型预测结果对比如图13所示。图中,预测结果越靠近对角线表明预测模型精度越高。则从图中可以看出: LGB+XGB+Hyb的预测结果明显优于其他模型,这表明提出的混合模型相较于XGB、LGB及Hyb模型适用性更强。 图12 各模型预测结果 图13 各模型预测结果对比 各预测方法评估指标值如表3所示。由表3可以看出: XGB+LGB+Hyb的R2值高于其他预测方法,MAPE值及RMSE值明显小于其他预测方法,这进一步证明了所构建的预测方法具有更强的适用性。 表3 各预测方法评估指标值 将10余座寒区隧道的冻结深度实际值与预测值进行对比,如图14所示。考虑到工程实践里对冻结深度的预测可接受1个数量级范围内的误差[1],故在图14中加入距实际值1个数量级的2条误差线,认为在该误差线范围内的预测值达到了精度要求。从图14中可以看出: 1)当冻结深度在1.5~2.0 m时,预测效果较好,均接近于实际值。2)当冻结深度值小于1.5 m或大于2.0 m时,预测值出现了偏差,这主要是由于在训练所构建的XGB-LGB预测模型时,输入的数据有73%的冻结深度值都处于1.5~2.0 m,因此使得在预测冻结深度值小于1.5 m或大于2.0 m时出现了偏差。 图14 模型预测值与实测值对比 1)各个断面沿径向的温度场分布规律与洞内气温密切相关。根据各断面围岩不同径深温度场的变化情况,可将围岩温度沿径向的变化划分为3个阶段,即快速变化阶段、缓慢发展阶段以及稳定阶段。 2)不同因素对冻结深度的影响程度由大至小依次是: 初始地温>最冷月平均气温>围岩比热容>围岩导热系数>衬砌导热系数>衬砌比热容。冻结深度与围岩导热系数、衬砌导热系数呈线性正相关关系,而冻结深度与最冷月平均气温、初始地温、围岩比热容呈线性负相关关系。 3)提出的XGBoost-LightGBM模型与传统单一模型相比预测精度较高,具有更强的适用性。 值得注意的是,不同的寒区隧道会因为气候等原因导致冻结深度趋于稳定时距洞口的距离不同,在距洞口300 m之后冻结深度趋于稳定这一结论在类似的地质、气候和工程条件下才具有一定的适用性。另外,在探究冻结深度各影响因素敏感性及显著性时并未涉及到各个影响因素间的相互作用(即交互性)。此外,XGBoost-LightGBM混合模型预测冻结深度的最佳适用范围为1.5~2.0 m,超过该范围的冻结深度预测值会出现一定的偏差。




4 冻结深度预测模型构建
4.1 预测模型介绍



4.2 建模过程
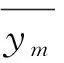
5 冻结深度预测结果与工程验证
5.1 预测结果分析



5.2 工程验证
6 结论与讨论
