求解整数线性规划问题的量子近似优化算法

戚 晗，何婉莹，邱 涛，Abdullah Gani

（1. 沈阳航空航天大学 计算机学院，沈阳 110136；2. 马来西亚沙巴大学 计算机与信息学院，亚庇 87000）

近年来，物联网、移动边缘计算、车载自组织网络（vehicular ad hoc network，VANET）发展迅速，随之而来的一些基站和服务器选址、资源分配调度等问题受到广泛关注。这些问题可以理解为在有限的可供选择的方案中，寻找满足一定约束的最好方案，因此类似此类问题可以归结为整数线性规划问题［1］。整数线性规划问题属于线性规划中的一种，其中又分为二元整数线性规划、混合整数线性规划等。随着问题规模的扩大，在约束条件的限制下寻找到整数线性规划问题最优解的时间复杂度较高。

随着“噪声中尺度量子”时代［2］的快速发展，量子优化算法逐渐受到关注，量子近似优化算法（quantum approximate optimization algo‐rithm， QAOA）在2014 年由Farhi 等提出［3］，被认为是在近年可以实现量子霸权的算法之一［4］。Willsch 等［5］、Herrman 等［6］以最大切割问题和2-SAT 问题为例分析了QAOA 的性能，发现在D-Wave量子退火计算机上的性能优于量子计算机模拟器。Bengtsson 等［7］使用超导量子处理器实现QAOA，可以提高找到精确覆盖问题最优解的成功概率。QAOA 变分态的对称性会使算法本身有一定的局限性，但是基于伊辛模型的QAOA 优于原始QAOA，且优于Williamson 算法［8］。目前，QAOA 被用于解决许多组合优化问题，使用QAOA 找到问题全局最优解的概率比较依赖于量子线路的迭代次数（即步长P）。然而，当QAOA 的步长P 很低时，找到近似最优解的概率很小。Azad 等［9］在使用QAOA 解决车辆路径规划问题时，迭代24次找到最优解的概率约为30%，当迭代次数更高时，概率并没有达到较高的水平。Zhang等［10］在使用QAOA 解决最小顶点覆盖问题时，迭代2 次时，概率低于20%；迭代10 次时，概率可以达到约80%。Vikstl 等［11］在使用QAOA 解决精确覆盖问题时，在迭代2 次时的单次测量下，找到最优解的概率为8.97%，需要重复多次测量才能提高概率。此外，QAOA 还被应用于哈密顿回路问题［12］和最大权独立集问题［13］。尽管成功概率因不同问题而异，但QAOA 无疑是解决组合优化问题的一种较好的方法。2020 年，Choi等［13］针对无线自组织网络中簇头选择的问题，采用量子经典混合方法求解簇头选择策略。为了让所选择的簇头具有较高的能效，将此问题定义为最大加权独立集问题，运用QAOA 求解最佳策略。2022 年，Fan 等［14］使用QAOA 解决图计算中最短路径问题，结果显示，QAOA 在参数选择和步长选择上优于经典算法和基于Grover 的最短路径算法，且需要的量子比特数更少。2023 年，Soloviev 等［15］为了解决许多传统方法无法解决的贝叶斯网络结构学习问题，采用基于3n（n-1）/2 个量子比特的QAOA 进行求解（其中n 为贝叶斯网络中的节点数量）。结果显示，在任何数据集上的性能都要优于经典和其他量子方法。在缩短整数线性规划问题的求解时间方面，QAOA 是一种有意义且可行的解决方法。

本文针对整数线性规划问题，提出一种基于改进目标哈密顿量的QAOA 的量子线路方法，提高在低迭代时找到最优解的概率并缩短程序执行时间。通过构造与整数线性规划问题对应的数学模型，将经典伊辛模型量子化，得到本文所要解决问题的目标哈密顿量。推导哈密顿量对应的量子门线路，并减少线路中使用的量子门数量。本文使用本源量子的py‐Qpanda框架进行模拟，验证了改进目标哈密顿量对找到基态概率和执行时间的影响。

1 资源分配问题的整数线性规划公式

为了便于理解这一类场景下的整数线性规划问题，本文以车载自组织网络为例进行说明。通过车载自组织网络实现车辆之间通信可以有效地避免出现交通拥堵和事故，因为司机可以获得超出可视范围内的实时路况信息。但是远距离车辆无法直接通信，需要合作通信来获取信息，合作通信需要使用中继车辆节点的资源，但每辆车的剩余资源、移动速度和位置都是不固定的。在这种情况下，需要考虑中继节点如何选择。如果中继节点集中在一辆车上，那么会造成这辆车过载，从而导致通信失败，所以中继节点的负载平衡十分重要，需要合理分配中继节点的资源。针对资源分配下的整数线性规划问题，本文以源节点代表需要请求计算资源的设备，以目标节点代表提供计算资源的设备。

假设目标节点具有相同的资源，源节点的资源需求量不同，那么影响延迟的主要因素即为通信距离。但是当目标节点的资源不足以处理所有请求时，会产生排队延迟。现在用G表示整个网络，V 表示所有源节点的集合，R 表示所有目标节点的集合，d 表示源节点和目标节点之间的通信距离。资源分配的目的是实现负载均衡的同时尽量减少通信延迟。每个源节点的资源需求表示为vl，xvr为二元决策变量。如果源节点与目标可以相连，则xvr为1，否则为0。此问题可以表述为

可选取的目标节点不确定是否每个都可以与全部源节点连接，但是需要确保总有一个目标节点可以为其提供资源。通信条件相同的情况下，访问距离越短，访问延迟越小，且距离越短，可以连接的概率也越大，所以将源节点与目标节点之间的距离表示为dvr， xvr同样为二元决策变量。如果源节点与目标连接，xvr为1，否则为0，此问题可以表述为

约束条件可以表述为

式中：n 为源节点的数目。式（1）和（2）为本文中的目标，式（3）为约束条件，即一个源节点只能分配给一个目标，不能分配给多个目标，规划范围内的所有源节点都要与相对应的目标连接，即所有源节点的请求都会受到相对应的目标的处理。与源节点相连的目标应该处理其所有的请求服务；一个目标节点可管理多个源节点；不考虑源节点与源节点之间、目标与目标之间的链路。

2 基于伊辛模型的量子近似优化算法

对于同一个问题，当设置的目标哈密顿量不同时，结果是不同的。在解决整数线性规划问题时，设置了两个不同的目标哈密顿量。一种是仅为问题函数（用Hp表示）求解目标哈密顿量；另一种是将问题函数和变形约束求和，并忽略公式中的常数，以获得改进的目标哈密顿量（用Hc表示）。以上两种方法用于设置不同的目标哈密顿量，为比较实验做准备。

QAOA 的核心是通过从初始哈密顿量的基态，经过P 步迭代演化至目标哈密顿量的基态，在这个过程中需要使用经典计算来完成参数的更新。图1 为QAOA 的算法结构图，它的线路是以初始量子态为生成元的酉变换和以目标量子态为生成元的酉变换乘积的累积。Hb为初始哈密顿量，以Hb为生成元的酉变换等于e-iHbβi，Hp为目标哈密顿量，以Hp为生成元的酉变换为e-iHpγi。其中βi和γi所代表的是不同的变分参数。

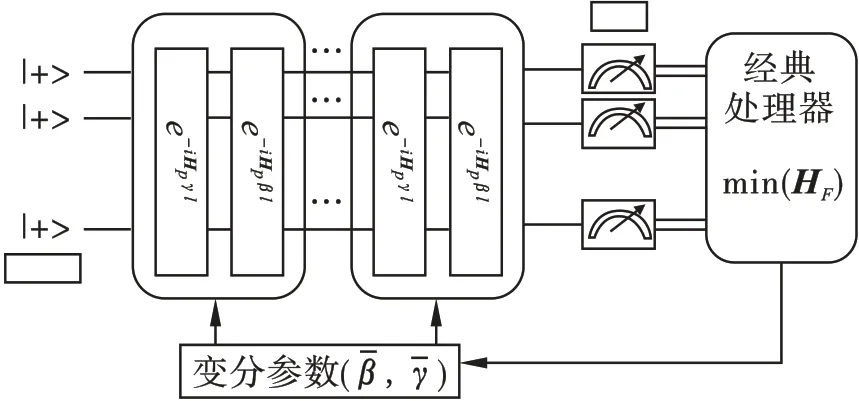
图1 QAOA的算法结构图

对于目标哈密顿量的设定，采用伊辛模型来实现，本文所描述问题的目标哈密顿量可以表示为HA+HB［16］，其中

使用二元决策变量xr∈{0，1}代替自旋变量sr∈{-1，1}，即

2.1 设置目标哈密顿量HP

在资源分配整数线性规划问题中，主要考虑两个方面，即通信延迟和工作负载。本文将通信延迟转化为通信距离，以HA为目标哈密顿量；将工作负载转化为源节点的需求量，以HB为目标哈密顿量。将公式展开，得到问题中

让A、B、C、D、E为

式中：C 和E 是常数，将自旋变量变为自旋泡利矩阵si→σzi，即得到最终目标哈密顿量

由于绝热量子计算和量子门电路模型的计算能力相同［17］，本文将使用门电路构造QAOA 的线路，经过推导，最终得到基于伊辛模型的目标哈密顿量是19 个CNOT 门、CZ 门和RZ门的组合，如式（9）所示

2.2 改进目标哈密顿量Hc

根据资源分配问题的定义，本文将目标哈密顿量改进为原始目标函数与约束条件函数之和，可以表述为

其中A'、B'、C'、D'、E'为

式中：C'和E'为常数，它只与哈密顿量的相位有关，对本征态没有影响［10］，所以可以进一步将其简化为

将自旋变量变为自旋泡利矩阵si→σzi，即得到最终目标哈密顿量，如式（13）所示

经过推导，目标函数Hc可以表示为5 个CNOT门、RZ门组合，如式（14）所示

2.3 初始哈密顿量

设定初始哈密顿量为泡利X算符在每个量子位上的和，如式（15）所示

其基态是泡利算符对应特征能量的张量积，如式（16）所示

经过推导初始哈密顿量是H 门操作，原始QAOA和改进QAOA的初始哈密顿量均为Hb。

3 仿真实验

本文使用基于python 的本源量子的pyQ‐panda 框架来执行QAOA，并解决整数线性规划问题下的资源分配优化问题实例（4，2）。其中，4 表示源节点的数量，2 表示目标节点的数量。实验所需的实际量子位N根据源节点和目标节点之间的通信链路确定。当源节点请求目标节点的资源时，中间距离对通信延迟和连接的可能性都有影响。如果距离超过其覆盖区域，则无法利用目标节点的资源。

例如（4，2），使用式（17）来描述问题（它是归一化数据），相应连接如图2 所示，覆盖区域分别表示E和F的可连接范围。

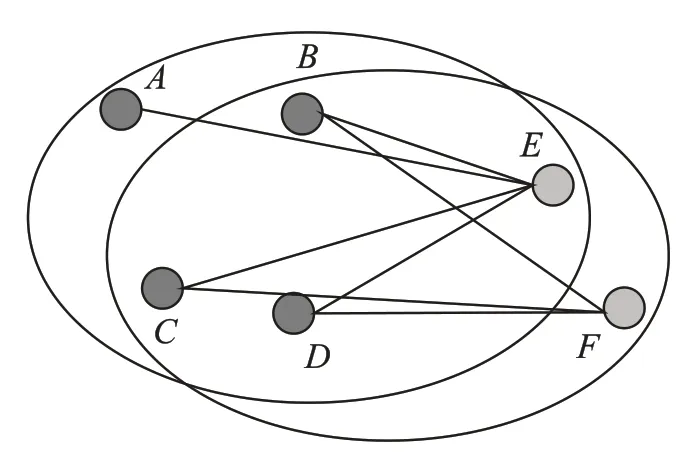
图2 问题示例（4，2）的连接图

如图2 所示，A 和F 之间的距离太大，超出了F 的通信覆盖范围，从而阻止了链路连接。实际距离应为∞，因此式（17）中使用1 表示无连接。为了编码这个问题，将每个量子位分配给图2中的每个链路，即如果使用了链路，则意味着对应的二进制决策变量为1，否则为0。为了使用QAOA，必须采取以下步骤：

（1）初始化线路，并加入初始哈密顿量基态所对应的量子门；

（2）通过初始化待优化的参数β和γ来确定量子门的初始旋转角度，根据参数生成更新的量子线路，然后测量期望值；

（3）将当前的参数通过经典计算机再次优化会得到一组新的参数，通过新的参数计算新的损失值，直到满足结束条件，即哈密顿量从初始基态演化到目标基态。

3.1 QAOA中参数更新方法对比

如何进行经典计算来更新参数至关重要，虽然也有使用张量网络技术［18］来寻找参数的策略，但是最常用的方法是使用优化器计算。本文对比了AdaGrad 优化器［19］、Adam［20］、Mo‐mentum［21］、RMSProp［22］和Vanilla Gradient De‐scent［23］5种优化器分别在原始和改进QAOA 中的性能。通过对比这5 种优化器，可以看出哪一种更新参数的方法最适用于本文所提出的问题。本文使用损失函数的收敛值来评价不同优化器对算法的影响。

首先针对原始目标哈密顿量Hp进行实验，不同优化器的性能如图3 所示，在步长P=2 且优化器迭代次数为200时，5种优化器所形成的损失函数值均不断减小，其中Momentum 优化器的整体损失函数值要低于其他优化器，但其前期波动较大，其余4 个优化器的损失函数收敛值相近。可以看出除了AdaGrad 优化器之外，其余的损失函数收敛很快，在开始迭代到50 次左右就可以稳定收敛在固定数值，且保持在-0.900 3，但是前期同样出现较小波动。AdaGrad 优化器虽然收敛不如其他优化器快，但是并没有任何波动。综合来说Momentum优化器虽然损失函数值更低，但是由于其波动较为严重，所以不适用于目标哈密顿量为Hp时的QAOA。

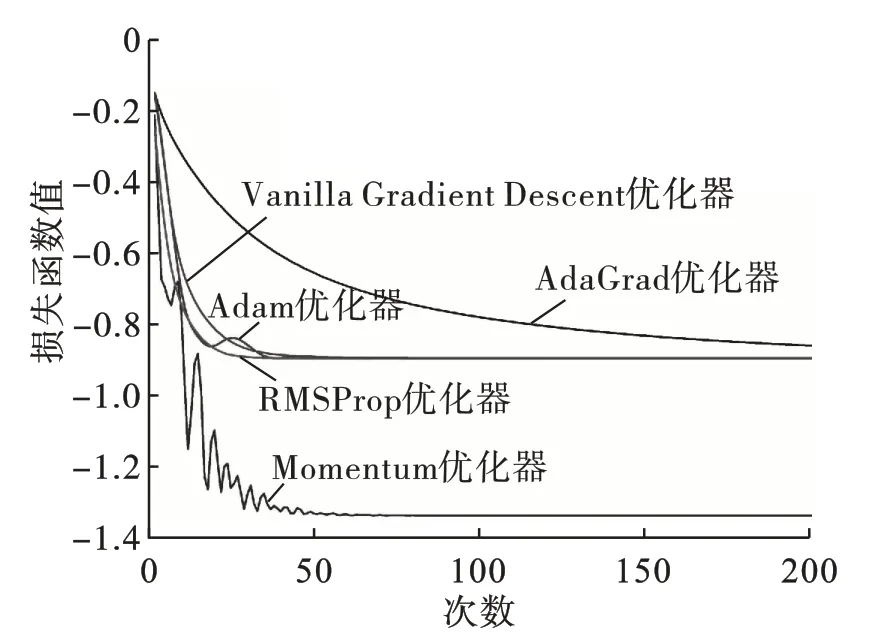
图3 不同优化器性能

改进目标哈密顿量Hc在不同优化方法下损失函数的变化如图4所示。在相同步长和迭代次数时，Hc的损失函数值均低于Hp，可以看到Adam、Momentum、RMSProp 和Vanilla Gra‐dient Descent 4 种优化器在迭代次数为50 时均可收敛，AdaGrad 优化器在迭代200 次时还没有明显收敛趋势，但当迭代次数为500 时可以收敛。Momentum 优化器在收敛前一直存在明显波动，这是因为引入历史梯度信息动量。Adam 优化器是基于Momentum 优化器和RM‐SProp 优化器提出的，在迭代次数为20～30 也有小范围波动，之后达到收敛状态。RMSProp优化器和Vanilla Gradient Descent 优化器没有波动，并且可以以较快的速度达到收敛值，其中Vanilla Gradient Descent 优化器的初始值要低于RMSProp 优化器。这与哈密顿量Hp存在一定差别，这是因为Hc与Hp本身存在差异，对于不同的目标哈密顿量，最合适的优化方法是不确定的。

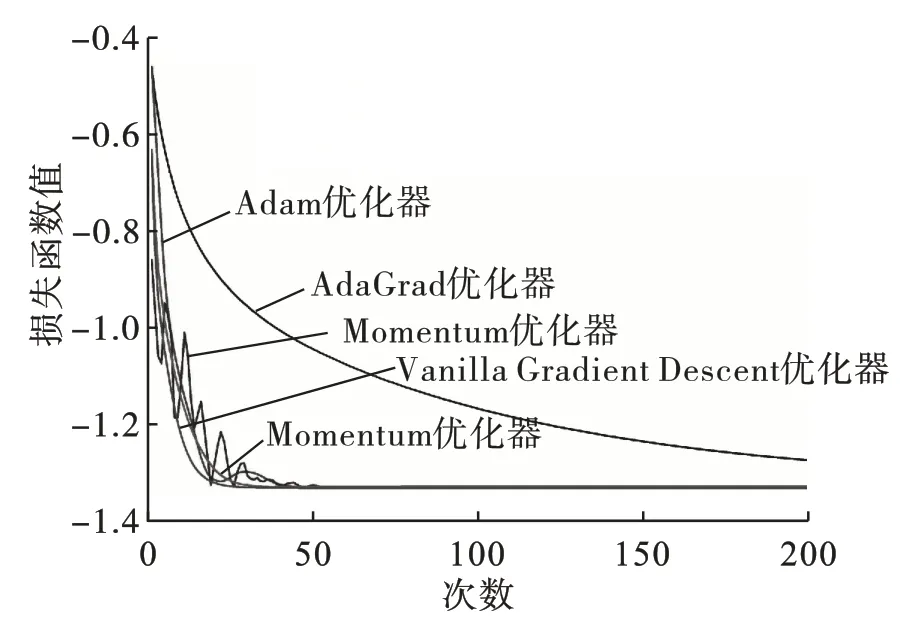
图4 Hc在不同优化方法下损失函数的变化

3.2 QAOA的不同目标哈密顿量性能对比

在实例（4，2）中，通信连接如图2 所示，边缘映射序列为｛A−E，B−E，A−F，C−E，C−F，D−E，D−F｝。一般来说，基于门电路的QAOA 使用量子门形成绝热演化过程，使得哈密顿量从初始基态演化到目标基态。最后测量并得到哈密顿量的目标基态，在这个问题中，对应的基态是|11100101〉，映射序列是｛A−E，B−E，C−F，D−F｝。当P=2时，找到目标基态的概率可以达到54.156 3%，对于低迭代级别来说这是非常高的成功率。然而，随着哈密顿量的改进，概率进一步增加到82.9%。概率分布如图5 所示。

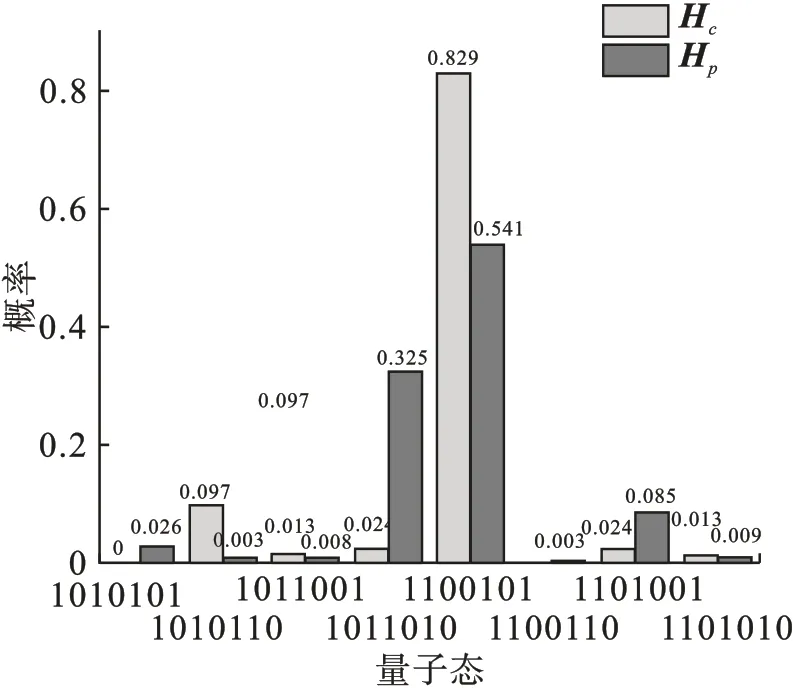
图5 不同哈密顿量求得最优解的概率

从图5 可以看出，目标哈密顿量为Hp时，所有解中概率较高的为“1011010”和“1100101”，虽然正确解“1100101”的概率高于“1011010”，但是极容易陷入局部最优解。而当目标哈密顿量为Hc时，正确解“1100101”的概率远高于其他解，与目标哈密顿量为Hp时相比，更加容易跳出局部最优，以一个较高的概率得到问题的正确解。

QAOA 的执行时间与量子门的数量密切相关。与原始目标哈密顿量Hp相比，改进目标哈密顿量Hc减少了量子门的数量，这影响了找到最优解的时间。如图6 所示，在同一设备上执行QAOA，随着步长P 的增加，时间显著增加，尤其是对于Hp。可以看出，尽管Hc的时间也随着P 的增加而增加，但增加的幅度没有Hp的大。在P=10 时，Hc的执行时间为Hp的19.16%，P=2 时Hc的执行时间为Hp的24.62%，Hc的平均执行时间为Hp的20.8%。这意味着当步长P 较大时，改进目标哈密顿量Hc的优势更明显。

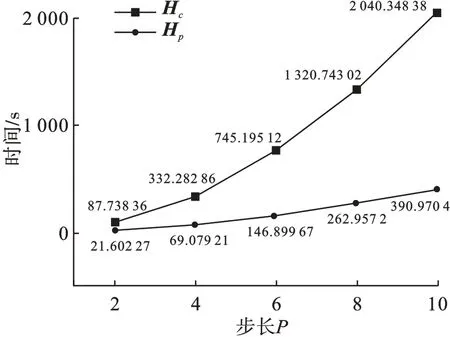
图6 不同哈密顿量的执行时间

3.3 时间复杂度分析

QAOA 是经典算法和量子算法的结合。经典部分通过经典优化器优化参数，其时间复杂度为O（poly（q）），其中q 是经典优化器迭代次数。本文中经典部分主要对比AdaGrad、Adam、Momentum、RMSProp 和Vanilla Gradi‐ent Descent 5 种优化器，其中Vanilla Gradient Descent每次更新需要计算整个数据集的梯度，且需要选择合适的学习率，学习率太小会导致收敛缓慢，太大则会导致收敛效果波动。Mo‐mentum 动量法是在随机梯度下降法（Stochas‐tic Gradient Descent， SGD）基础上提出的，SGD 具有较快的下降速度，但因为方差频繁更新，容易出现剧烈波动的情况，但也正是因为SGD 的波动性使其可能收敛到更好的局部最优。Momentum 动量法则可以抑制SGD 的摇摆情况，在减轻波动情况的同时，更容易收敛到局部最优。在本文实验中Momentum优化器前期波动，最终收敛值更低。AdaGrad 在训练过程中累计平方梯度越来越大，导致学习率过早减少，迭代时收敛缓慢。在本文实验中AdaGrad 优化器在迭代200 次时没有达到明显收敛效果，速度缓慢。RMSProp 解决AdaGrad学习率急剧下降的问题，加速效果更好，收敛速度快。在本文实验中，RMSProp 优化器收敛速度最快。Adam 是Momentum 动量法和RM‐SProp 的结合体，下降速度快，参数更新稳定，但是可能存在小波动。在本文实验中Adam 优化器在迭代过程中出现小范围波动，下降速度最快。

量子部分需要完成从初始状态到目标状态的演化，这部分的复杂度相当于量子态演化的时间，即O（poly（P）），其中P 是迭代次数（即步长）。QAOA 是从绝热算法演变而来的，该系统可以通过使用绝热算法来保证开始状态是基态，并且最终状态也是基态，但是成本相对较高（例如时间成本）。相比之下，QAOA 运行时间相对较短，但获得基态的概率也受到限制。因此，如果增加迭代次数P，总体成功概率也会得到一定的提高。

根据上述分析，QAOA 的时间复杂度如式（18）所示

从式（18）可以看出，QAOA 在时间复杂度上的性能要优于其他经典算法，因为QAOA 的复杂性与所需要求解问题的大小无关，而经典算法的复杂性随着问题规模的增加呈指数增长。

4 结论

本文利用QAOA 解决了与资源分配相关的整数线性规划问题，将节点间的链路映射到量子位来编码哈密顿量Hc、Hp和Hb。通过从原始的目标哈密顿量Hp转换到改进的目标哈密顿量Hc，量子电路的运行时间和所需量子门的数量都显著减少。此外，本文分析并比较了原始目标哈密顿量Hp和改进的目标哈密顿量Hc对找到近似最优解的影响。实验结果证明了QAOA 在解决这些问题方面的有效性，即使有少量的迭代，该算法也有很高的成功率。例如，当目标哈密顿量是Hp时，成功率是54.156 3%，而当它是Hc时，概率增加到82.9%。这种低迭代水平转化为实现算法所需的低电路深度，证实了其在近期量子机器上的可行性。由于QAOA 的时间复杂性不受问题大小的影响，因此它更适合大规模和多节点场景。此外，哈密顿量Hc的电路需要更少的量子门，这可以缩短执行时间，平均执行时间为Hp电路的20.8%。在未来，将会对QAOA 的内部结构进行改进，发现更有效的参数更新技术，并将不同的模型应用于不同的组合优化问题。