涪陵页岩气井射孔及滑移段套管变形特征分析

易先中 孙养清 万继方 陈辉 姚秀田 吴霁薇 张仕帆

(1.长江大学机械工程学院 2.湖北省智能油气钻采装备企校联合创新中心 3.中国石油集团工程技术研究院有限公司非常规油气工程研究所 4.中国石油化工股份有限公司胜利油田分公司孤岛采油厂 5.中国地质大学未来技术学院)

0 引 言

2021年我国累计开采页岩气230亿m3，其中涪陵页岩气田年生产能力达100亿m3，是国内第一个实现商业开发的页岩气田[1]。涪陵页岩气井压裂过程中套管变形问题显著，带来了页岩气开采成本增加、产量大幅降低等不良后果，严重制约着我国页岩气的开发进程[2]。

近几年，众多学者针对套管变形问题进行了研究。刘鹏林等[3]认为断层滑移是套管剪切变形的主要因素，并因此建立了一种考虑断层上、下部地层的断层滑移模型及滑移量计算方法。陈朝伟等[4]对威远、长宁和昭通区块9口井的37处24臂井径测井数据进行统计处理，分析该区块的套管变形特征，结果表明剪切导致的套管变形占60%。李皋等[5]通过研究页岩膨胀对套管变形的影响，认为密集射孔将释放因页岩膨胀而导致的膨胀应力，这是套管变形的主要原因。姜广彬等[6]建立了考虑上覆地层位移与出砂空洞的射孔套管模型，分析认为，出砂井射孔套管在轴向载荷作用下的变形不同于在径向挤压作用下的变形，微小的上覆地层就能导致射孔套管发生大变形。

综上所述，大部分学者认为套管变形主要是压裂过程中产生的裂缝以及地层对套管所产生的应力等造成的，并且地质条件及材料属性影响着套管的形变特征。为了缓解涪陵区块套管变形问题，结合前人对套管变形的研究，本文以焦页4HF井为例，针对套管变形最为严重的射孔段及滑移段建立套管-水泥环-地层耦合模型，开展数值分析，探究套管的形变特征及其规律。

1 套管变形情况

图1a为油气开采示意图。由图1a可看出，油气开采阶段套管受力情况复杂，需结合现场情况进行分析。通过涪陵区块出现不同程度套管变形8口井的40臂井径、磁测厚、磁定位显示，射孔井段所在套管受压裂影响较大，套管变形严重，其中3口井钻塞遇阻。结合测井地质参数分析认为，压裂作用导致该区块部分断层地应力改变，引起断层被激活而对套管产生剪应力[7]，如图1b所示。

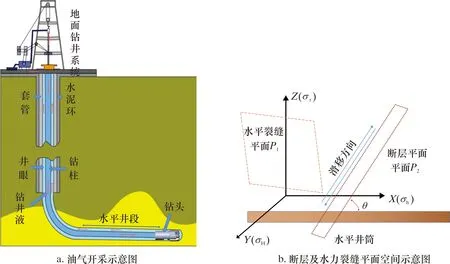
图1 套管井下及滑移示意图Fig.1 Schematic diagram for downhole casing and slip

由图1可知，压裂导致套管变形的原因主要体现在以下2方面：

(1)射孔时发出的巨大冲击力使套管承受巨大载荷，射孔周围的套管因此而产生变形和裂纹。若持续输出较大载荷，将会导致套管疲劳裂纹扩展，最终损坏套管[8]。套管外侧的酸液、压裂液等各种液体，会对套管产生腐蚀，也会极大地削弱材料抗挤压强度，同时这些液体还对套管施以挤压力，使套管变形损坏[9]。

(2)套管在射孔完井后出现多处孔洞，使圆柱表面的均匀性遭到破坏，导致套管的强度降低。同时，射孔位置及其附近的套管也是地层滑移、压裂、挤压力等外力作用最强的井段，加之油井长期开采，容易造成套管损坏[10]。

由此可见，引起套管变形的主要原因是射孔后套管强度降低，地层滑移及多次压裂等。因此探究以上情况下套管变形的特征对涪陵页岩气的高效开采具有指导意义。

2 井下套管力学分析

井下管柱力学行为十分复杂，必须结合实际的工程约束条件进行研究[11]。本文与焦页4-4HF、10-SHF、21-5HF井作业报告相结合展开分析计算。由Ariy’s应力函数可设非均匀应力场中套管、水泥环、地层系统的应力函数为[12]：

φ=A+Blnr+Cr2+Dr2lnr+(Kr2+Fr4+M/r2+H)cos2θ

(1)

式中：φ为系统的应力函数；A、B、C、D、F、K、M和H为无因次系数；r为径向距离，mm；θ为周向角，(°)。

应力分量函数为：

(2)

将式(1)和式(2)联立即可得到套管、水泥环、地层的各应力分量表达式：

(3)

式中：i取1、2、3，分别代表套管、水泥环和地层；σi为系统径向应力，MPa；σσi为系统周向应力，MPa；τrθi为系统剪切应力，MPa；Bi、Ci、Ki、Fi、Mi、Hi分别代表套管、水泥环和地层与上述力学模型有关的常数。

3 数值分析模型

3.1 模型建立

以ø139.70 mm×10.54 mm的P110管材为分析对象，建立套管模型进行分析，射孔参数如表1所示。

表1 焦页4HF井射孔参数Table 1 Perforating parameters of Well Jiaoye 4HF

为了便于分析计算，假设条件如下：①射孔过程中射孔方向垂直套管壁面、孔眼的位置与设计位置一致；②射孔之后形成的孔眼标准，未产生椭圆等其他形状，同时套管的孔眼没有裂纹和毛刺产生；③射孔段及周围套管为壁厚均匀的圆柱形。

套管的弹性模量E1取210 GPa，泊松比为0.3，屈服强度为758 MPa；水泥环的弹性模量E2为7 GPa，泊松比为0.22；围岩的弹性模量E3取35.5 GPa，泊松比为0.18。为了便于分析套管受不同类型地应力作用的情况，采用如图2a所示的矩形地层模型，分析由于地层坍塌及滑移情况下上覆地层施加于模型的垂直应力σv与水平主应力σh，采用如图2b所示的柱形地层模型分析周向挤压p1和内压p2下套管的变形特征[13]。模型几何参数如下：地层为1 m×1m，水泥环外径199.70 mm，套管外径139.70 mm，套管内径118.62 mm。

图2 套管-水泥环-地层组合模型Fig.2 Casing-cement sheath-formation composite model

3.2 网格划分

用SolidWorks软件建模与装配后，将所建模型导入Workbench中进行多区域网格划分，网格大小为35 mm。为了提高网格质量，对水泥环网格加密为10 mm，对套管网格加密为5 mm。根据网格的正交质量显示，最小为0.846 39，最大为1，平均值为0.973 7，满足数值分析对准确性的要求。

3.3 模型验证

套管模型如图3所示。采用弹性力学理论计算[14]与数值分析相结合的方式进行模型验证。

图3 套管力学分析与边界条件Fig.3 Mechanical analysis and boundary conditions of casing

圆筒内外受均布压力属于轴对称应力问题，可以采用轴对称问题的通解。结合应力边界条件和位移单值条件，可得方程的Lame解[15]：

(4)

式中：r1为套管内径，mm；r2为套管外径，mm；p1为套管外压，MPa。

为了计算套管的理论应力值，取r等于r3带入公式(4)，可采用薄壁圆筒方法简化计算，当r1等于r3时，σr1趋于0，则式(4)可化为：

(5)

式中：r3为套管中径，mm；σr1为套管径向距离为r1的正应力，MPa；σθ1为套管径向距离为r1的周向应力，MPa。若将r1=59.31 mm、r2=69.85 mm、p1=20 MPa带入式(5)，可得σθ1=143.36 MPa。

图4所示最大压力取143.39 MPa，考虑到r1/r3小于1，故实际计算值略小于仿真计算值，验证了模型的正确性。

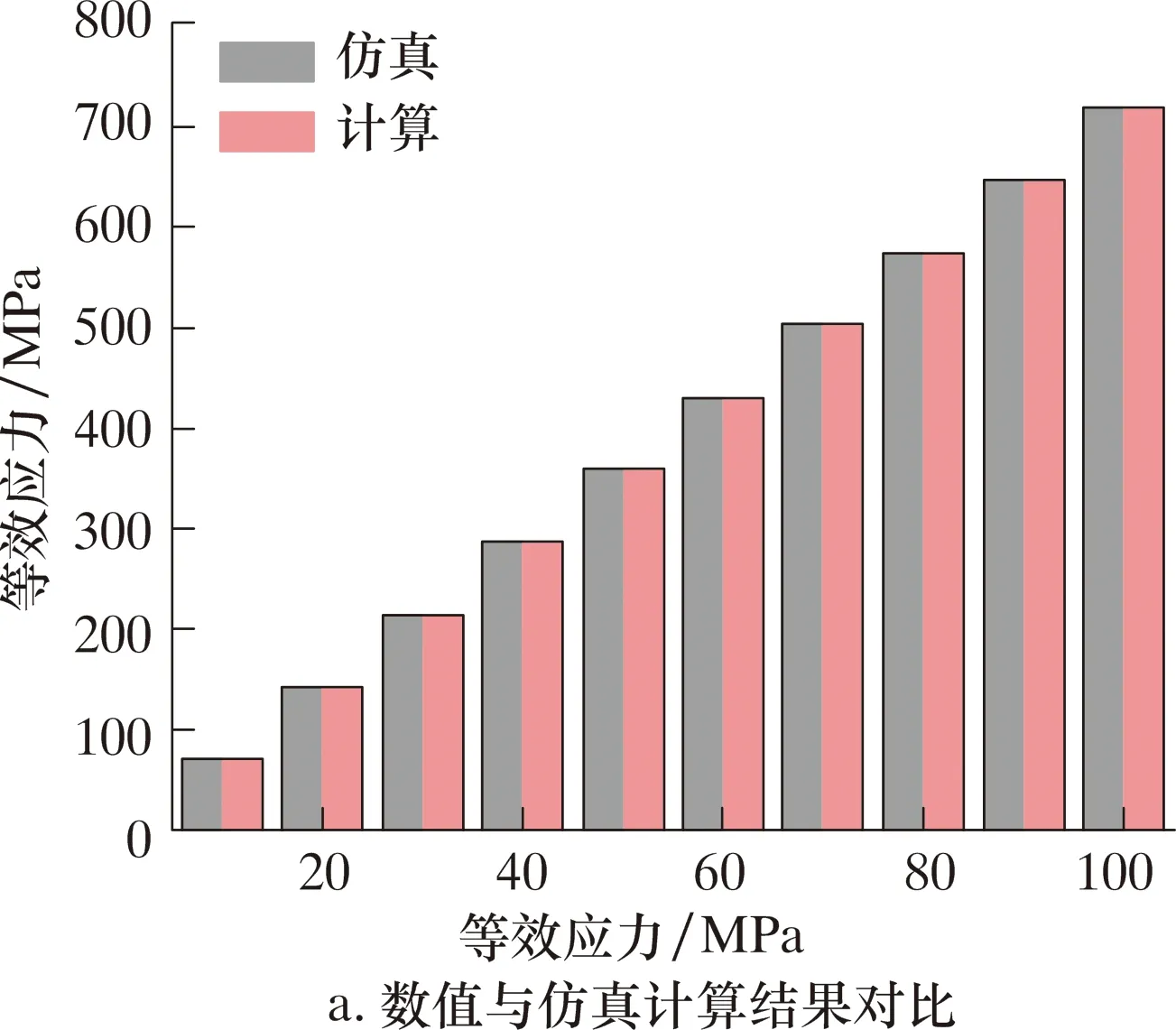
图4 套管数值分析与理论分析Fig.4 Numerical and theoretical analysis of casing

4 套管变形特征分析

4.1 地应力对套管变形的影响

基于柱形、矩形2种地层受压情况，以焦页4HF井射孔井段为例，分析套管与水泥环的最大等效应力。载荷约束如图5所示：A、a分别为上覆压力与挤压力；B、b、c为固定约束面。套管与水泥环、水泥环与地层间的摩擦因数取μ1=μ2=0.2。

图5 载荷约束Fig.5 Load constraints

在压裂车的高压作业下，地质条件将发生较大变化，取围岩压力范围为20～100 MPa，探究套管与水泥环的应力变化规律。图6为40 MPa外压下套管射孔前后等效应力云图。

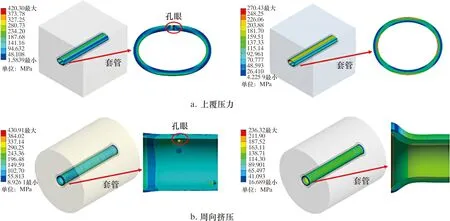
图6 40 MPa外压下套管射孔前后等效应力云图Fig.6 Cloud chart for equivalent stress before and after casing perforation under 40 MPa external pressure

如图6a所示，40 MPa外压下，套管在上覆压力下呈椭圆形，孔眼处出现应力集中现象，其应力较无损套管最大应力值增大55%；如图6b所示，套管在周向挤压下与未挤压交界面出现颈缩现象，射孔段最大应力较无损套管增大82%。其应力变化情况如图7所示。

图7 射孔前后水泥环与套管等效应力曲线Fig.7 Equivalent stress curves of cement sheath and casing before and after perforation

由图7a可知，水泥环在射孔前后其等效应力变化较小。由图7b可知，无损套管受周向挤压与上覆压力的等效应力曲线相近，线性拟合斜率分别为6.65与6.79，但射孔套管在周向挤压下的线性斜率为13，此时套管易产生较大变形。

4.2 射孔段套管变形特征

保持20孔/m的射孔密度不变，建立30°、45°、60°、90°、120°和180°共6种不同相位角，6～20 mm 8种不同孔径的套管模型。

结合现场数据，取地层挤压力为20 MPa，套管内压70 MPa，探究射孔参数对套管变形的影响规律。为了减小边界约束对射孔分析的影响，取套管长2 m，并且使1 m射孔段位于模型中段，如图8所示。

图8 不同相位角射孔模型Fig.8 Perforation models with different phase angles

为了直观地显示套管在不同射孔角度与孔眼直径下的变形情况，隐藏水泥环与地层后，放大250倍变形系数，取18 mm孔径下的套管等效应力云图，如图9所示。

图9 不同相位角射孔套管等效应力云图Fig.9 Cloud chart for equivalent stress of casing perforated at different phase angles

为了探究其变化规律，将所有的射孔参数通过数值仿真进行计算，在不改变信号趋势和宽度的情况下提高数据的精度，并通过Savitzky-Golay卷积平衡算法来平滑数据，结果如图10所示。

图10 不同相位角射孔和孔径对套管与水泥环的最大等效应力曲线Fig.10 Maximum equivalent stress curves of casing and cement sheath under perforation with different phase angles and perforation sizes

在不同相位角的情况下，随着孔径的增大套管的最大等效应力随之不断增大。45°、90°相位角射孔下套管等效应力值最小，且当孔径为16 mm时，水泥环最大等效应力最小。

4.3 滑移段套管变形特性

根据对套管变形情况的统计分析，在出现断层、天然裂缝以及层理发育区，套管变形的概率较高，占比约为61.7%[16]。采用2 m×1 m×1 m的地层模型进行分析，设套管内压为75 MPa，页岩滑移面为斜向下45°方向，如图11所示。

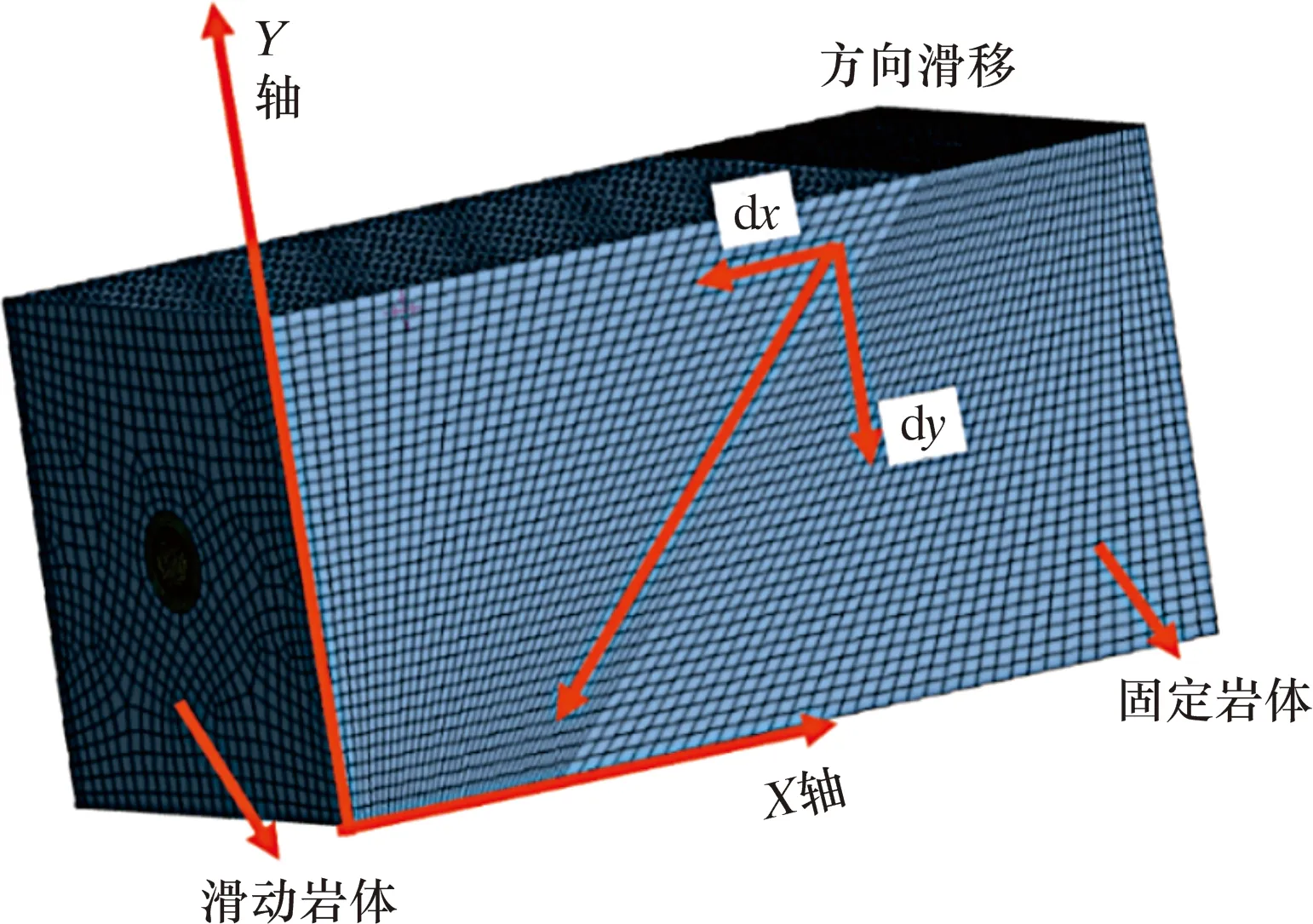
图11 页岩滑移模型Fig.11 Shale slip model

为了便于分析，设置裂缝面的滑移距离dy=dx，滑移距离分别为0.5、1.0、1.5、2.0、2.5和3.0 mm，共6组。为了便于分析滑移条件下套管的变形情况，将其30倍比例放大后如图12所示。

套管在滑移面处出现变形，将严重影响后续的施工效果。由以上数值分析可知，在45°页岩滑移状况下，套管的最大等效应力位于断面上接触点，如图13所示。由图13可知，套管变形量与最大等效应力随滑移量增大而增大，沿45°方向滑移4.243 mm，套管的最大等效应力值为634.91 MPa，总变形量为3.957 mm。因此预防和减小页岩滑移是防止套管形变的重要措施。

图13 页岩滑移量对套管与水泥环的形变特征影响Fig.13 Deformation characteristics of shale slippage on casing and cement sheath

4.4 水泥环对套管变形的影响

在滑移段套管变形特征分析的基础上，通过改变水泥环性能来探究其对套管变形的影响。为了直观地展示变形特征，分析不同水泥环泊松比在X、Y方向滑移1 mm时套管的最大等效应力，放大40倍后取不同泊松比的套管应力云图，如图14所示。

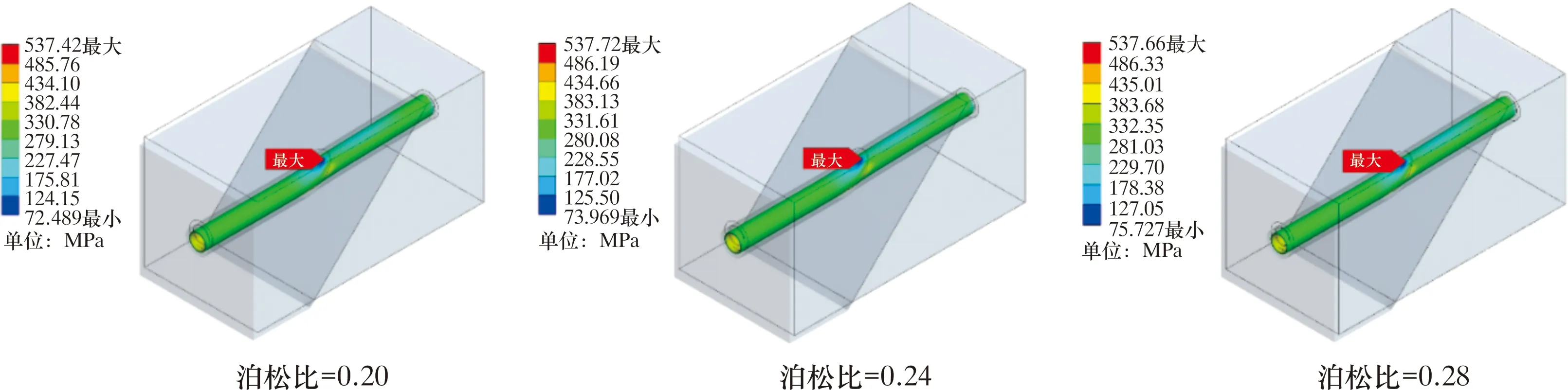
图14 不同水泥环泊松比的滑移套管等效应力云图Fig.14 Cloud chart for equivalent stress of slip casing with different Poisson’s ratios of cement sheath

为了减小天然裂缝、水力压裂等对套管变形的影响，仅采用提高套管钢级和加厚套管壁厚等措施效果非常有限，水泥环的材料属性很大程度也影响套管的使用寿命[17]。因此，设水泥环弹性模量为7 GPa，取0.2～0.4共10种条件下的泊松比进行数值分析，结果如图15所示。

图15 水泥环泊松比对套管变形特征影响曲线Fig.15 Influence curve of Poisson’s ratio of cement sheath on casing deformation characteristics

由图15a可知，随着泊松比减小套管形变量不断减小，但效果并不显著。因此，通过增大水泥环泊松比来预防套管变形不可取。由图15b可知，当水泥环弹性模量为7 GPa，泊松比为0.26时，套管的应力值最大，减小泊松比至0.26以下或撤去水泥环，套管等效应力有一定的降低。

水泥环弹性模量与泊松比对套管变形特征的共同作用效果如图16所示。

图16 水泥环弹性模量与泊松比对套管变形特征影响曲线Fig.16 Influence curve of elastic modulus and Poisson’s ratio of cement sheath on casing deformation characteristics

由图16可见，增大水泥环的弹性模量在页岩滑移处能在一定程度减小套管的最大等效应力，但因此也改变了地层力的传递系数，使套管的总变形量相对增大。弹性模量减小时，出现应力峰值时的泊松比值也相应降低。因此，需结合现场地质条件及施工要求合理选择水泥环的材料属性，以减轻套管形变与损坏的状况。

5 套管变形地面试验装置

为了测试受损套管承受内压时的应力应变情况，搭建了地面液压试验台。试验台主要包括CB200-5.5超高压试压泵、井口装置、套管堵头、连接器、压力表、高压管线、封隔器和应变片等。

试验步骤如下：将试验套管与井口装置套管接口端连接，井口装置另一端通过特定的接口与堵头连接，并通过内置封隔器将套管另外一侧堵住。井口装置两侧接口可与高压软管连接以施加液压。由于套管变形尺寸较小，可在安装完套管后在其表面贴上应变片，后续可通过示波器实时观察套管各位置的应力变化，从而推断出套管变形特征。该试验装置与连接情况如图17所示。

图17 套管压力试验现场连接情况Fig.17 Field connection status of casing pressure test

通过向装置施加10、20、30、40及50 MPa压力，并且经过保压后判断该装置是否满足密封性要求，试验合格后，可将该装置应用于后续的套管变形研究。

6 结 论

结合涪陵区块套管变形的数据及地质参数，以焦页4-HF井分段压裂为例，通过建立套管-水泥环-地层耦合模型，分析射孔参数、45°方向页岩滑移、水泥环材料属性对套管变形的影响规律及变形特征，结论如下：

(1)ø139.7 mm×10.54 mm的P110无损套管受周向挤压与上覆压力时的应力变化率相近，但射孔后，套管在周向挤压下应力变化较快，此时套管易产生较大变形。射孔套管孔眼内边缘为应力集中点，45°、90°相位角射孔相较于30°、60°、120°和180°相位角射孔对套管强度的影响较小，且当孔径为16 mm时，水泥环所受最大等效应力最小。

(2)45°方向页岩滑移情况下，套管最大等效应力位于滑移面上接触点，微小的滑移量将导致套管严重变形。当页岩滑移量4.243 mm时，套管的总变形量为3.957 mm。

(3)增大水泥环的弹性模量时，在页岩滑移处能减小套管的最大等效应力，但套管的总变形量也相对增大。当水泥环弹性模量为7 GPa时，减小或增大泊松比至0.26以上均能有降低套管的最大等效应力，但对预防套管变形效果并不明显。

(4)设计了套管受内压地面试验装置，搭建了室内试验平台，经过测试其保压效果合格后，可为套管变形分析提供试验平台保障。