超深井卡瓦悬挂器套管力学强度有限元分析

2023-09-14练章华万智勇吴彦先史君林赵朝阳

石油机械 2023年9期

练章华万智勇吴彦先史君林赵朝阳

(1.西南石油大学油气藏地质及开发工程国家重点实验室 2.中国石油新疆油田分公司工程技术研究院)

0 引言

随着深井超深井的广泛开发，大尺寸套管深井越来越多，井口坐挂载荷控制变得困难。坐挂载荷过大会导致井口下沉及卡瓦牙对套管损伤大等问题，过小可能导致套管头密封性能差等问题。若要避免这些问题，需要对井口卡瓦悬挂器与套管损伤的力学机理进行深入的理论和试验研究[1-3]。井口装置作为油井井筒完整性的重要一环，其承压能力及密封性能直接影响服役状况下的安全[4-8]，必须进行井口试压测试。在该过程中往往需要施加较高的压力，并且在套管轴向载荷以及悬挂器卡瓦夹持力等共同作用下，使得井口位置套管受到较大的复合载荷，极易造成井口管柱变形、损坏等现象，严重影响正常作业的安全[9-11]。

目前，关于套管失效方面的研究[12-17]主要集中于地层深处套管在体积压裂、地层滑移等因素下的失效分析，而有关试压生产过程中井口套管柱的损伤、断裂研究相对较少。曾经有学者开展过卡瓦悬挂器套管受力问题理论研究[18-20]，其基本方法是采用静力学原理对井下封隔器上的卡瓦进行力学分析，得到卡瓦锚定时卡瓦牙的正应力计算公式，但是对于井口坐挂吨位或卡瓦效应的套管拉伸极限载荷方面还缺乏系统的理论研究。而将卡瓦夹持过程中对套管的径向载荷视为均匀载荷，只能得到套管内壁为塑性失效区，无法计算卡瓦牙吃入套管过程中套管外壁由于应力集中而产生的塑性破坏，并且拉梅公式解析解无法计算套管外壁由于卡瓦牙引起的应力集中，但有限元法能够解决此问题。为此，笔者将建立套管卡瓦悬挂器有限元计算的3D模型，开展有限元仿真模拟分析，对井口卡瓦式悬挂器中套管的塑性破坏进行安全评价，以期为控制或避免套管断裂失效提供理论依据和指导，同时也为卡瓦悬挂器套管的设计、各种安全施工作业提供理论依据。

1 悬挂器及套管卡瓦效应极限载荷

目前国内已经多次出现井口套管断裂情况。图1为新疆某油田超深井X1井口卡瓦部分高钢级155V套管断裂照片。从井口套管断裂情况以及裂口可知，套管断裂发生在卡瓦下部，且卡瓦部分套管存在较深的牙痕，裂口还没有完全断掉是因为其发生裂纹时被卡瓦抱住，而卡瓦下部没有被卡瓦抱住的套管则掉入了井中。结合大量现场研究和分析可知，图1中井口套管断裂失效的主要原因是卡瓦悬挂器的卡瓦牙在套管外壁产生牙痕，导致套管在悬重作用下产生应力集中，并且在各种作业过程中产生的交变载荷同时作用于该位置，所以卡瓦下部附近套管在过大悬重载荷作用下发生套管缩径变形，在各种交变载荷作用下，发生井口套管断裂，同时也有可能是套管质量及服役环境问题，如材质、腐蚀介质、恶劣受力环境等造成的。

图1 X1井井口卡瓦部分套管断裂照片Fig.1 Photos of casing failure at slip part of wellhead of Well X1

现场使用的卡瓦式井口套管悬挂器结构如图2所示，由卡瓦、卡瓦座、密封圈、支撑座以及四通等主要部件组成。

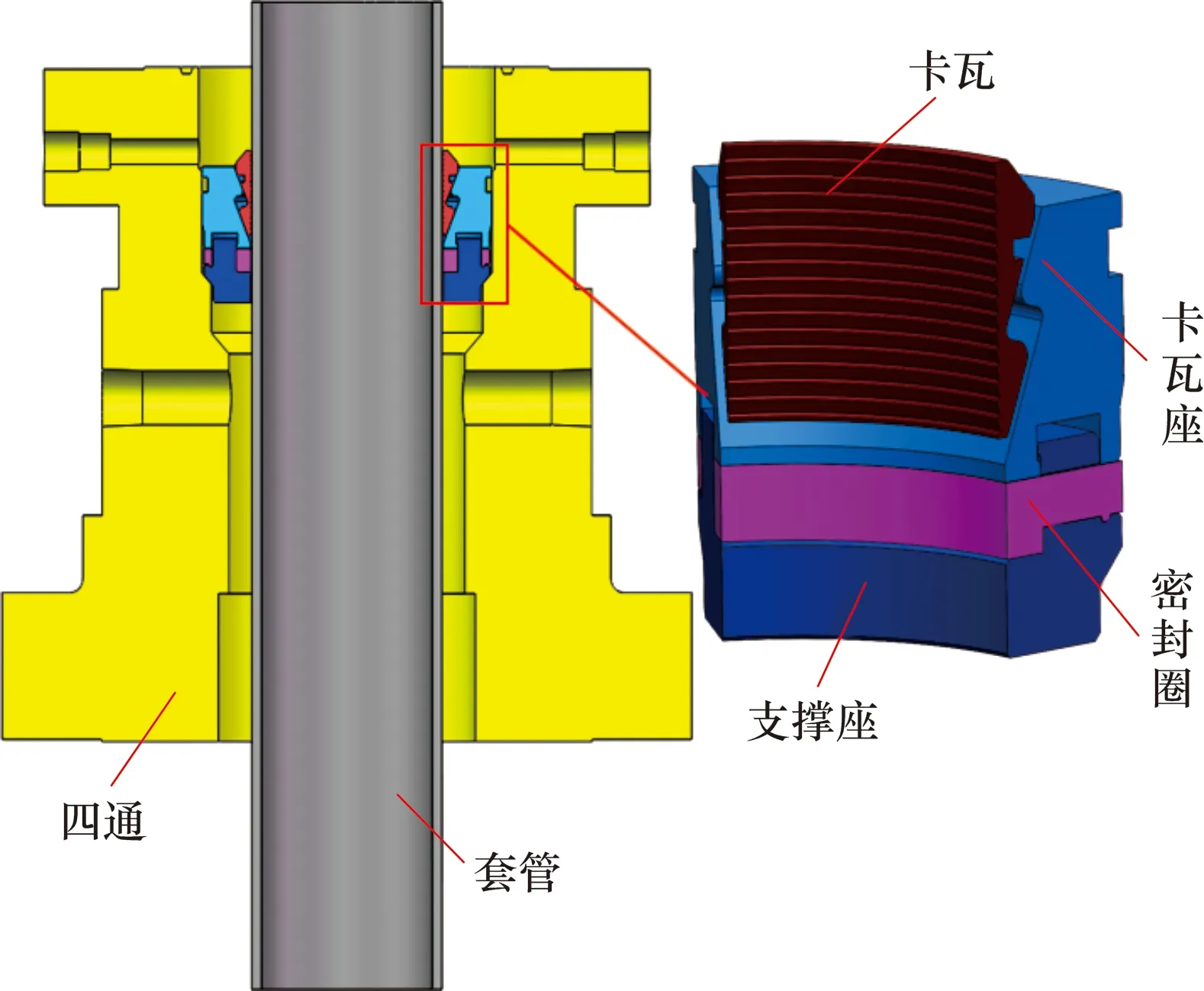
图2 卡瓦式悬挂器结构示意图Fig.2 Schematic diagram for structure of slip-type hanger

在卡瓦式悬挂器坐挂过程中，支撑座刚好卡在四通的台阶上，卡瓦座底面通过橡胶密封环和背面与四通接触实现固定，于是在受力分析时只需要考虑套管、卡瓦和卡瓦座即可。套管头卡瓦受力如图3所示。卡瓦咬紧套管是卡瓦与套管柱相互作用受力的过程。卡瓦刚开始咬紧套管时，其主动力来自于卡瓦与套管外壁的初始摩擦力。套管自重和下放冲击力经锥面传递、放大并反作用于卡瓦，使卡瓦将套管径向抱紧，直到卡瓦不能滑动为止。此时卡瓦与卡瓦座直接通过斜面接触，套管下落带动卡瓦微小下滑继续相互挤压；但由于卡瓦座位置固定不变，卡瓦牙受挤压咬入套管，产生一个巨大的挤压力N2，从而产生足够的摩擦力，使得套管达到力学平衡。如果套管悬挂载荷继续增大，则卡瓦会由于受到更大的挤压力继续咬入套管，直到达到新的力学平衡状态。

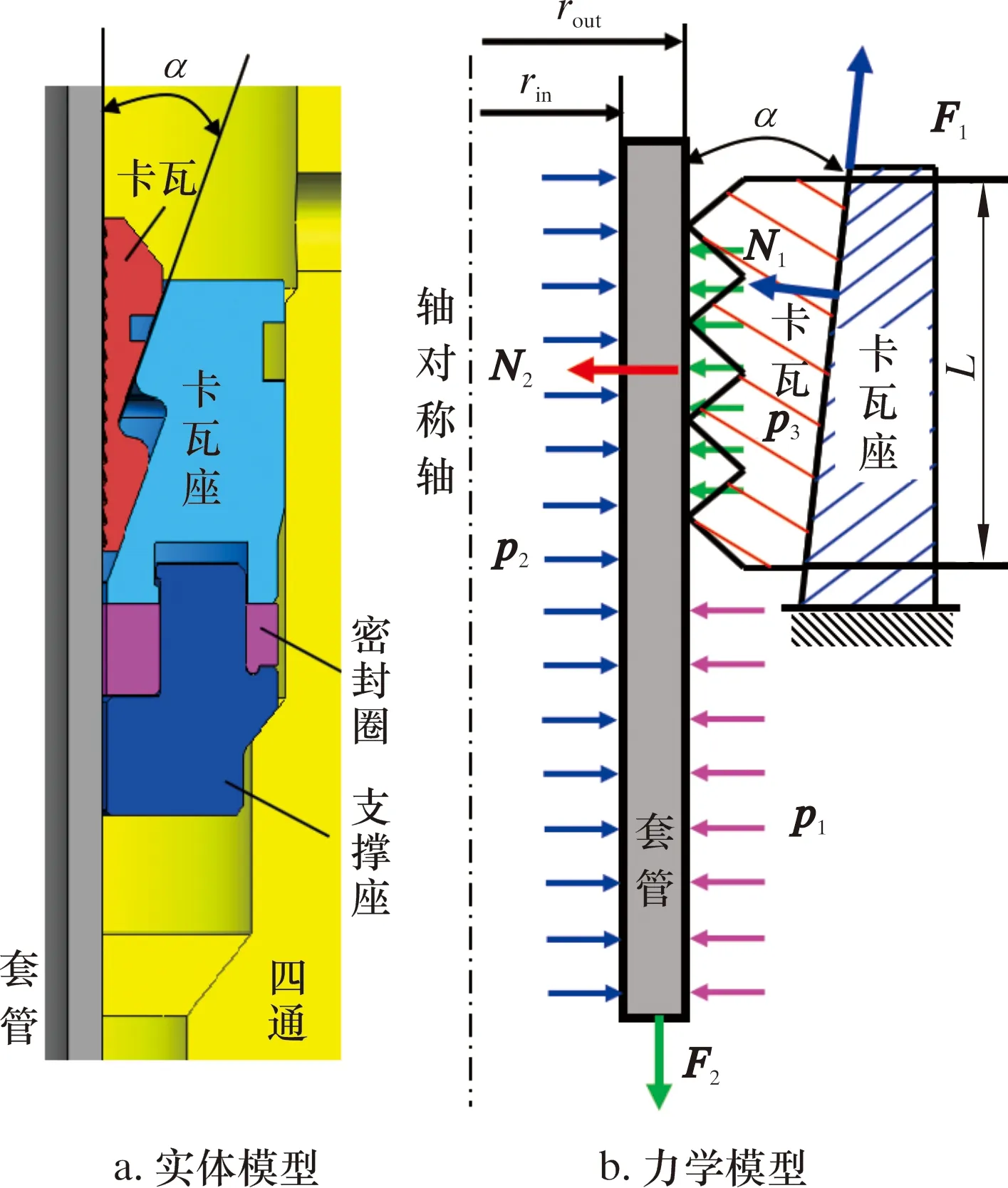
图3 套管-卡瓦结构轴对称力学模型Fig.3 Axisymmetric mechanical model of casing-slip structure

卡瓦套管悬挂器简化力学模型如图3所示。井口卡瓦悬挂器受到的外载荷主要有：各种作业中套管受到环空压力p1、井筒内的生产压力p2、夹持套管的悬重F2，以及F2产生的卡瓦部分外压力p3。N1为卡瓦与卡瓦座之间总法向力；N2为套管和卡瓦之间总挤压力；F1为卡瓦与卡瓦座之间总切向力；F2为套管轴向载荷(悬重)；p1为套管外压，p2为套管内压；p3为F2引起的卡瓦部分套管外壁平均压力。

根据材料力学第四强度准则理论[21-23]，当套管内壁的Mises等效应力达到屈服应力σs时，根据图3b中的力学模型，可推导出卡瓦悬挂套管的拉伸极限载荷，即卡瓦效应拉伸极限载荷Tks，计算模型如下：

(1)

Ts=σsA1

(2)

(3)

AL=2πroutL

(4)

(5)

式中：Ts为无卡瓦效应时的套管轴向拉伸极限载荷，N；μ为摩擦因数；K为横向载荷系数；AL为卡瓦侧向面积，mm2；A1为套管截面面积，mm2；σs为套管屈服强度，MPa；α为卡瓦背面半锥度，(°)；L为卡瓦有效长度，mm；rin、rout分别为套管内、外半径，mm。

在坐挂过程中，井口套管不存在图3中的内外压力p2和p1，只有轴向载荷F2及其引起的横向载荷N2产生的外挤压力p3的共同作用。因此由式(1)可以计算出套管的卡瓦效应拉伸极限载荷Tks，该拉伸极限载荷Tks可为下部套管长度或悬重控制提供理论依据。

当套管坐挂和固井后，在各种作业或生产工况下，图3中将存在内、外压力p2和p1的作用。该内、外压力也会影响卡瓦部分套管内的应力分布，这是个复杂的力学过程，用解析解无法计算，只能用有限元法进行仿真模拟计算和评价。

2 卡瓦悬挂器套管受力有限元分析

2.1 套管卡瓦悬挂器基本参数

本文根据新疆某油田超深Xl井，在拆采油四通更换密封件提起采油四通时，发现生产套管管壁上发生横向断裂(见图1)，其使用的ø232.5 mm W型卡瓦悬挂器的卡瓦结构有效长度为143 mm，卡瓦背面半锥角为24°，各接触面之间的摩擦因数为0.25。该X1井套管外径为232.5 mm，壁厚为16.75 mm，钢级为155V，线质量约为89.64 kg/m，井深约为7 809 m。由于所有构件均为钢材，泊松比为0.3，弹性模量为210 GPa，其余强度参数如表1所示。

表1 卡瓦悬挂器及套管各材料力学参数Table 1 Mechanical parameters of slip hanger and casing materials

根据以上参数以及式(1)～式(5)，可计算出无卡瓦效应和有卡瓦效应的套管极限载荷，即卡瓦效应的套管拉伸极限载荷，如表2所示。从表2可知，由于存在卡瓦效应，导致套管在卡瓦部分的拉伸极限载荷由12 380 kN降低到了7 010 kN，降低了43.4%。因此理论上在坐挂套管时，下部悬挂载荷必须控制在7 010 kN以内。

表2 坐挂过程中套管的极限载荷变化对比Table 2 Comparison of ultimate load changes of casing during setting process

2.2 有限元模型建立

由于该悬挂器有6瓣结构尺寸相同的卡瓦，且与套管一起呈轴对称结构，为了减小计算工作量，提高计算速度，根据有限元理论，将该卡瓦悬挂器建立为轴对称的3D有限元力学模型，如图4所示。其材料力学参数如表1所示。卡瓦、卡瓦座与套管相互之间为非线性接触模型，在卡瓦座外壁施加固定约束，卡瓦齿面与套管、卡瓦背面与卡瓦座接触面分别设置摩擦接触参数。下部端面施加悬重产生的拉力F2，同时在套管外壁、内壁分别施加压力p1和p2。为提高计算效率及精确度，在有限元网格划分时，对卡瓦与套管、卡瓦背面与卡瓦座等接触部位进行网格加密处理。

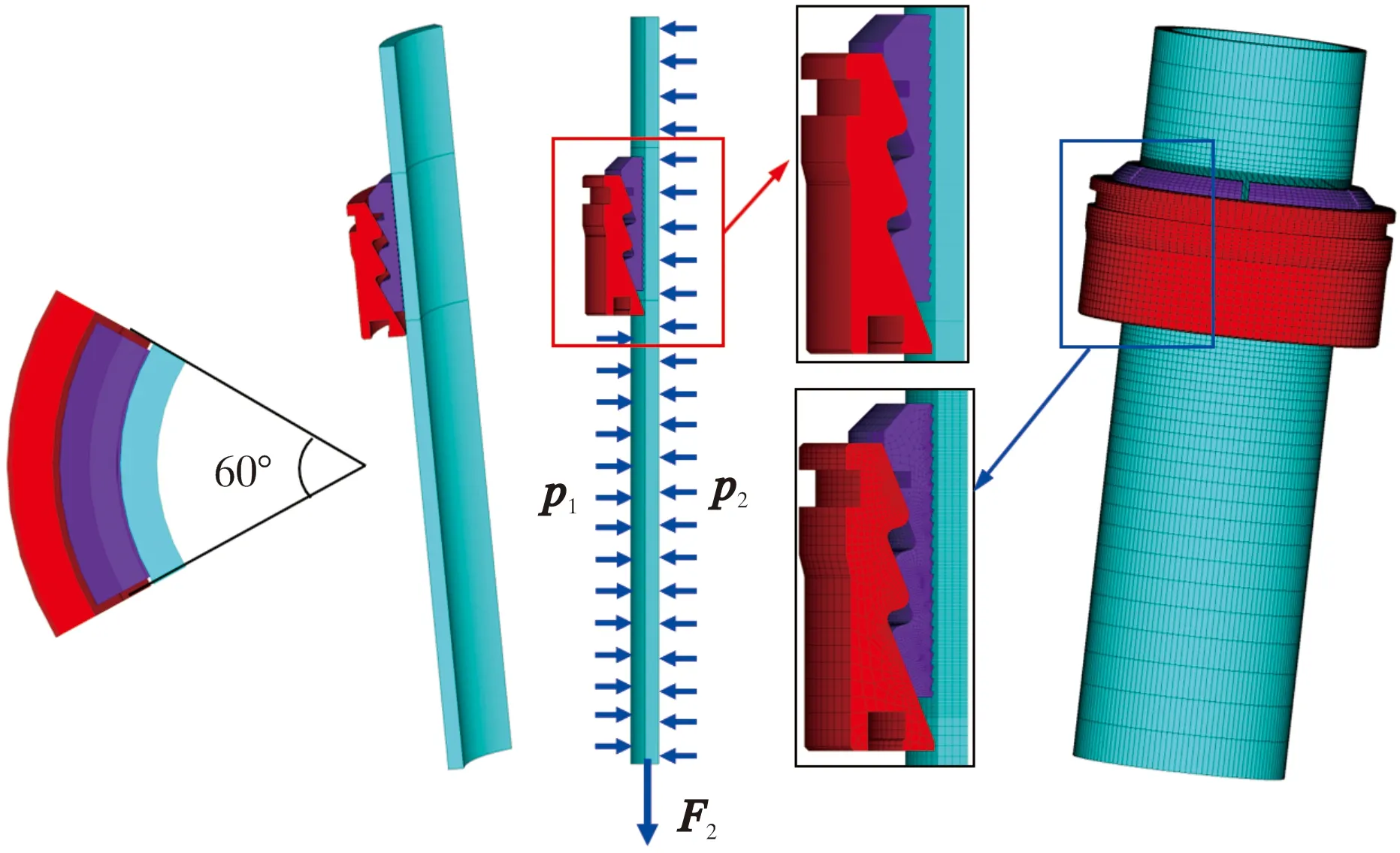
图4 悬挂器结构有限元力学模型(对称模型)Fig.4 Finite element mechanical model of hanger structure ( symmetric model)

2.3 坐挂过程套管极限载荷及其下深分析

套管在坐挂过程中，只有轴向载荷F2及其引起的横向载荷N2产生的外挤压力p3的共同作用。根据图4的有限元模型，逐渐增加轴向载荷F2，取出每个计算载荷下卡瓦部分套管外壁的最大Mises应力，通过大量的有限元仿真模拟计算，得到坐挂过程中套管内最大Mises应力随轴向载荷的变化关系，如图5所示。

图5 坐挂过程中套管内最大应力随轴向载荷的变化关系Fig.5 Variation of maximum stress in casing with axial load during setting process

从图5可知，套管坐挂过程中，卡瓦部分套管外壁的最大Mises应力随着轴向载荷的增加呈非线性增加，当轴向载荷达到6 400 kN时，套管上的应力达到其屈服应力1 069 MPa，开始进入塑性变形破坏，即有限元仿真模拟计算出卡瓦效应的套管极限载荷为6 400 kN，小于表2中理论公式计算结果7 010 kN，为理论公式(1)计算结果的0.913倍。这主要是卡瓦效应的应力集中引起的，且有限元仿真模拟计算结果比较接近实际工况，可以通过大量的计算来修正理论公式(1)。本文研究的卡瓦结构套管理论拉伸极限载荷公式(1)的修正系数为0.913。也就是说，如果遇到同样结构尺寸的卡瓦型号，其套管卡瓦效应的极限载荷可以通过理论公式(1)结果乘以修正系数0.913得到。

图5中轴向载荷F2=7 000 kN时的有限元计算结果如图6所示。

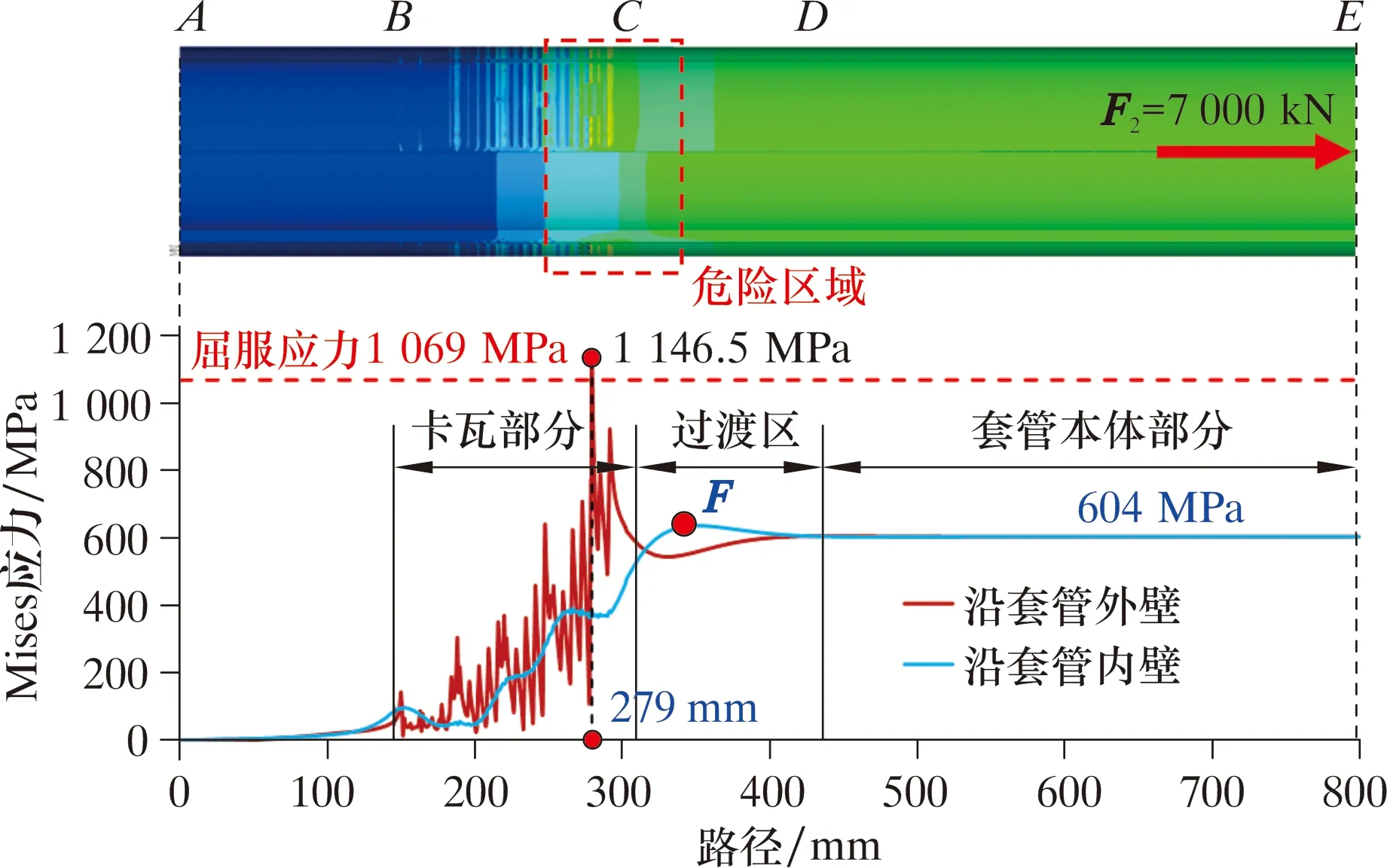
图6 套管应力云图及其内、外壁路径应力变化关系Fig.6 Cloud chart of casing stress and stress variation along inner and outer walls of the casing

由图6可知，沿套管外壁，在卡瓦部分，距离套管顶部A点位置为279～300 mm的套管出现塑性屈服区域，其最大应力为1 146.5 MPa，超过套管的屈服应力1 069 MPa。该区域是最危险位置，现场套管断裂位置也发生在此处。在图6中卡瓦部分，由于卡瓦牙齿引起的应力集中，卡瓦部分套管外壁的应力沿路径频繁交变增加，且大部分高于套管内壁应力，但只有外壁应力超过了屈服应力1 069 MPa，所以套管断裂失效的裂纹首先发生在套管外壁。

从图6中过渡区路径曲线可知：套管内、外壁应力发生交变，与卡瓦部分相反，其内壁应力高于外壁应力；远离过渡区的套管本体部分，其内、外壁路径上的应力曲线趋于重合，套管本体部分内、外壁应力相等，为604 MPa，这是因为本体只受7 000 kN的拉伸载荷作用，该拉伸载荷除以其横截面积也刚好等于604 MPa，表明计算工况正确。

卡瓦悬挂器处，套管的轴向载荷F2主要来自于下部套管的悬重。该悬重取决于套管的长度，如果井筒全部掏空，悬重为套管在空气中的重力；如果井筒内充满钻井液或清水，则套管悬重为空气中的重力减去其在液体中的浮力。根据图5计算卡瓦效应套管的极限载荷为6 400 kN，考虑套管段重力以及清水密度，可计算出卡瓦悬挂器套管的下深，如表3所示。从表3可知，如果井筒完全掏空，文中研究的X1井套管下到7 809 m大于7 140 m时，处于不安全状态。但是如果井筒内充满清水，在浮力作用下，其下深为8 175 m，大于设计井深7 809 m，可满足安全要求。因此，在下套管时，建议向井筒灌满清水或钻井液，以便降低套管悬重，保证其安全坐挂。

表3 卡瓦悬挂器套管安全下深Table 3 Safe setting depth of slip hanger casing

套管坐挂时，套管内、外无压力，仅受轴向载荷作用，根据表3中的计算结果可得出结论：该卡瓦悬挂器套管的极限载荷为6 400 kN，只要坐挂套管时，其轴向载荷在6 400 kN以内，卡瓦悬挂器套管不会发生塑性变形破坏。

2.4 作业工况套管塑性失效分析

套管在卡瓦悬挂器中坐挂固井后，在实际作业中，套管内、外壁同时受到内、外压力，但是作用效果会相互抵消，仅受到内压或外压作用时为套管受力最恶劣工况。在作业过程中，井筒内压为0时，只有环空压力变化的套管塑性变形破坏情况。

根据图4的有限元模型，轴向载荷从0增加到7 000 kN，作业过程中，套管外压p1分别为0、50和70 MPa时，通过大量计算，可得套管外壁最大Mises应力随轴向载荷及其外压的变化关系，如图7所示。从图7可知：套管外壁最大Mises应力随着轴向载荷及其外压的增加而增加；当Mises应力达到155V套管的屈服应力1 069 MPa时，套管外壁开始发生塑性变形。根据图7的计算结果，套管发生塑性破坏的极限载荷如表4所示。从表4可知，作业过程中外压越高，卡瓦部分套管承受的极限载荷越小，当外压达到最大设计压力70 MPa时，极限载荷只有4 500 kN，因此在作业施工时应严格控制套管环空压力。

表4 不同作业外压下卡瓦效应套管的极限载荷Table 4 Ultimate load of slip effect casing at different external pressures

将图7中环空最大压力p1=70 MPa时的最后一次计算结果进行应力分布云图分析，即当坐挂轴向载荷F2=7 000 kN，套管内压p2=0，按最恶劣工况进行计算，结果如图8所示。

图8 外压70 MPa时套管应力分布云图Fig.8 Cloud chart of casing stress distribution at 70 MPa external pressure

由于受到卡瓦牙的夹持作用，套管外壁出现条状非均匀分布的应力带。图8中Mises应力最大值为1 143.6 MPa，位于卡瓦部分套管的外壁，超过155V套管的屈服应力(1 069 MPa)。图8a中红色区为套管塑性破坏区，发生在套管外壁卡瓦牙齿咬入位置，且套管外壁塑性区只有少部分。套管外壁卡瓦牙附近的应力为900.0～1 143.6 MPa，见图8a～图8c中的黄色区域，其分布深度见图8c中ABC位置。此时卡瓦部分套管内壁应力为350～550 MPa，处于弹性变形，即卡瓦部分套管内的应力呈现非均匀分布，尤其是套管外壁非均匀程度较严重，其外壁牙痕上存在的应力集中是套管裂纹起裂、断裂的主要原因。

图8中过渡区为卡瓦部分套管与下部套管本体的交接部分。从云图上看，该部分套管内壁应力为黄色区，即应力在900～1 069 MPa之间；外壁应力为绿色区，即应力在550～750 MPa之间过渡区套管同样处于非均匀应力状态，只是其非均匀程度比卡瓦部分套管的非均匀程度轻。

从图8可知，远离卡瓦的套管本体部分应力呈现均匀分布，受力情况比前2个部分优良。如果套管发生断裂破坏，首先将发生在卡瓦部分以及过渡区位置，而发生在套管本体上的概率较小。

将图8中内、外壁沿最大应力路径数据取出进行分析，结果如图9所示。由图9可知，沿套管外壁路径，在卡瓦部分距离套管顶部A点位置280～300 mm处的套管出现塑性屈服区域，其最大应力为1 143.6 MPa，超过套管的屈服应力1 069 MPa。该区域是最危险位置，现场套管断裂的位置也发生在此处。过渡区套管内壁F点附近应力达到了屈服应力1 069 MPa，即套管内壁也出现了塑性变形破坏区。而图6中的工况，此时套管内壁F点应力约为630 MPa，远低于屈服应力。图9工况中套管内、外壁均出现了塑性变形区，因此套管在卡瓦部分或过渡区均有可能发生断裂失效破坏，并且在图9中远离过渡区的套管本体部分，其内、外壁路径上的应力曲线趋于平稳，但是套管本体部分内、外壁应力不相等，分别为977和925 MPa，其差异是外压70 MPa引起的。

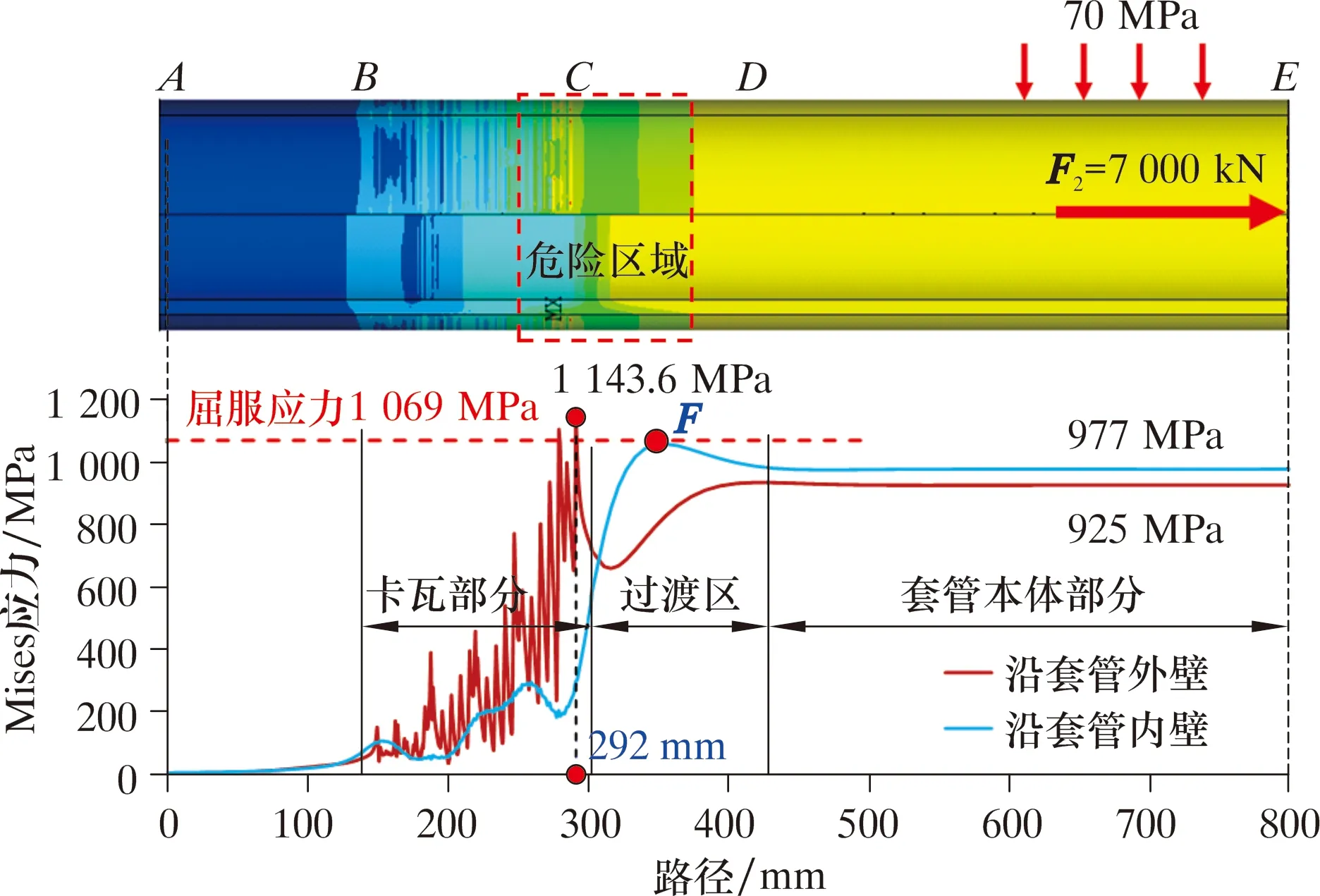
图9 沿套管内、外壁应力分布曲线Fig.9 Stress distribution curves along inner and outer walls of casing

3 卡瓦应力分析

在图8工况下，卡瓦上的应力分布如图10所示。图10中红色区为超过卡瓦屈服应力835 MPa的塑性变形区。由于卡瓦牙比较尖锐，吃入套管时产生了较强的应力集中，所以卡瓦牙附近有较宽的塑性硬化区，而卡瓦金属材料在屈服后存在一定的塑性硬化。由于材料硬化作用，卡瓦的屈服强度将会提高，同时卡瓦牙受套管挤压，卡瓦背面有卡瓦座支撑，卡瓦始终处于安全状态，现场数据也证明了这一点。虽然卡瓦处于塑性变形，但是仍能满足现场使用要求。

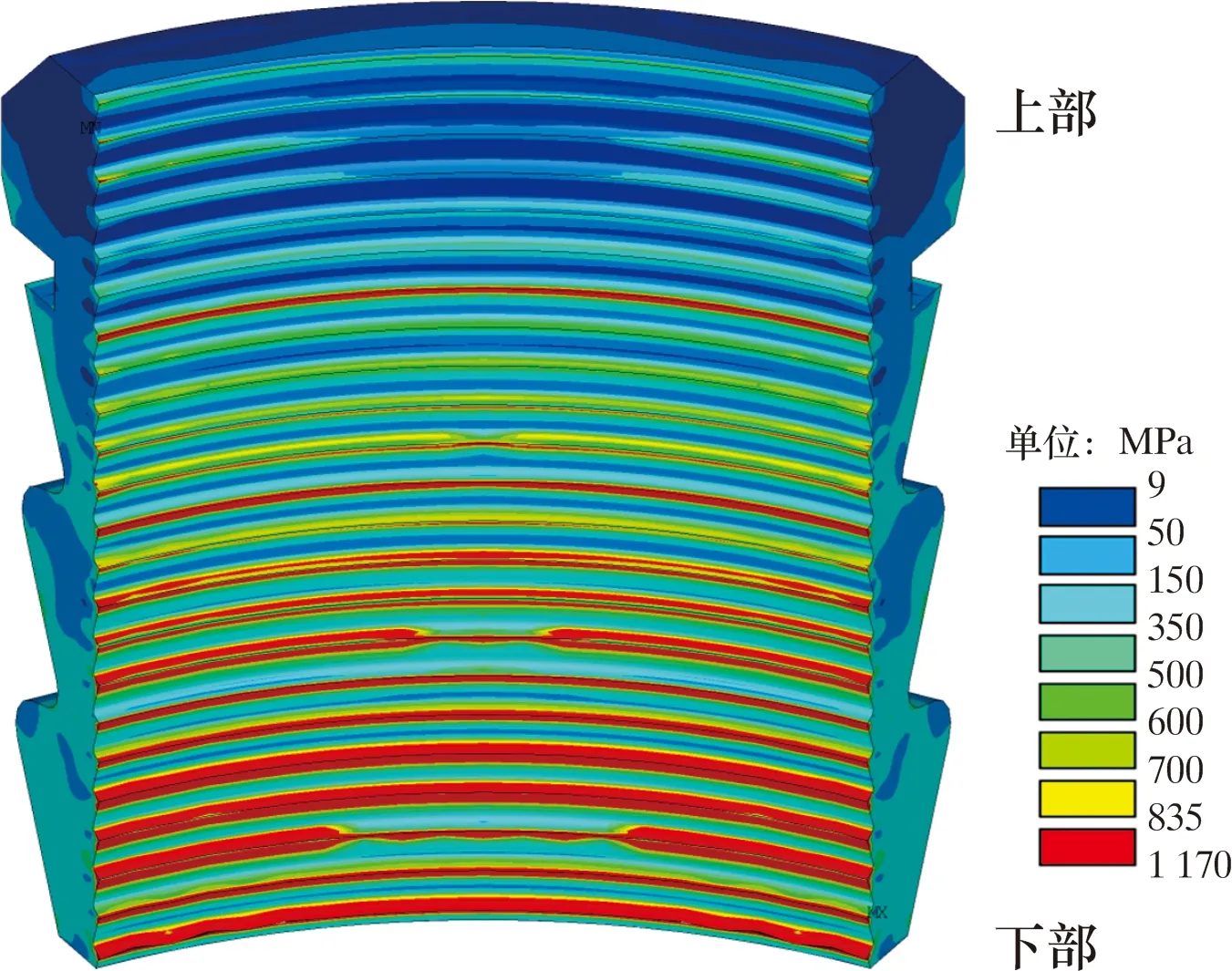
图10 外压70 MPa作用下卡瓦应力云图Fig.10 Cloud chart for stress of slip at 70 MPa external pressure

从卡瓦应力分布云图可知，卡瓦下部塑性区较多，上部塑性区逐渐减小甚至消失。主要原因是下部卡瓦牙咬入套管后将承担主要载荷，向上的每一圈应力逐渐递减，因此卡瓦下部受力较大，从图8卡瓦部分套管外壁的应力分布也可以得出同样的应力变化规律。因此，建议选择无齿痕的卡瓦夹持套管，或者采用全金属密封的心轴式悬挂器，避免卡瓦悬挂器造成套管损伤破坏。