基于改进SimCSE的无监督句嵌入方法

郭江华，苑迎春，2+，王克俭，2，何 晨

(1.河北农业大学 信息科学与技术学院，河北 保定 071001；2.河北农业大学 河北省农业大数据重点实验室，河北 保定 071001)

0 引 言

预训练语言模型BERT(bidirectional encoder representations from transformers)经过有监督微调(fine-tune)后展示出了强大的文本表征能力[1]。然而在没有微调的情况下，BERT便失去了良好的句嵌入表征能力[2]。模型嵌入表征方面的现有研究表明，大多数语言模型学习到的嵌入在向量空间上的分布并不均匀[3，4]：计算句嵌入时，高频词的词嵌入将会主导句嵌入，难以体现差异性[5]；而低频词的词嵌入分布较稀疏，存在表征语义能力较弱的“空洞”[6]。这些问题限制了模型的句嵌入表征能力。

最近的研究表明，对比学习(contrastive learning)可以有效提高句嵌入分布的均匀性[5，7]。SimCSE(simple contrastive learning of sentence embeddings)[7]就采用了对比学习方法，在无监督情况下通过dropout[8]作为数据增强方式构建正样本，并采用批内负样本策略，有效提高了BERT在无监督情况下的句嵌入表征能力。然而，无监督SimCSE仍有不足之处：一方面它只基于dropout构建正样本，构造方式有待丰富；另一方面由于dropout机制本身带来的训练与测试的不一致性，模型参数自由度更高，影响模型的泛化能力[9]。

本文基于无监督SimCSE提出无监督句嵌入学习方法SimCSE-PSER(unsupervised SimCSE combining positive sample enhancement and R-Drop)，采用dropout和位置嵌入扰动联合作为数据增强方法，从而在相同语义下构造具有更大差异性的正样本；并引入R-Drop正则化方法[9]，使用KL散度(Kullback-Leibler divergence)对模型生成的句嵌入分布进行正则约束，降低模型在训练和预测时的不一致性。

1 相关工作

近年来，无监督句嵌入表征研究进展迅速。Li等[6]提出BERT-flow模型，通过可逆映射将BERT的向量空间映射到各向同性的标准高斯分布空间；Huang等[10]提出BERT-whitening方法，采用线性变换校正BERT的句嵌入协方差矩阵并执行降维操作，从而达到与BERT-flow相近的效果。此类后处理方法虽然提升了句嵌入的表征效果，但是无法对模型本身进行调整，提升空间有限。Zhang等[11]提出IS-BERT模型，对各句的词嵌入提取n-gram特征作为局部特征，句嵌入作为全局特征，把最大化局部特征与全局特征的互信息作为训练目标。但是此方法没有考虑句嵌入间的分布，影响训练效果。

在无监督句子表征研究中，采用对比学习的方法表现优异。Carlsson等[12]提出无监督模型BERT-CT，此方法在训练时使用共享初始参数的两个模型对句子对进行编码，将相同句子看作正样本，不同句子看作负样本。但是此方法负样本利用率较低，并且在预测阶段仅使用其中一个模型，训练效率不高。Yan等[5]提出ConSERT模型，在模型初始层进行数据增强，对每个句子通过指定数据增强方法生成正样本，将同训练批次内的其它样本作为负样本。但是此方法仅在模型单层进行数据增强，正样本质量有待提升。

相比以上方法，Gao等[7]提出的无监督SimCSE模型使用预训练语言模型本身的dropout机制作为数据增强手段构造对比学习所需正样本，相对当前同类方法性能获得显著提升。但是，无监督SimCSE仍存在相同语义正样本差异性不足、采用dropout进行数据增强带来训练与预测阶段不一致性的问题。本文的工作将基于无监督SimCSE的框架并针对其不足展开。

2 SimCSE-PSER方法

2.1 无监督SimCSE

SimCSE是对比学习方法中的一种，在无监督情况下采用批内负样本策略，即将一个样本同训练批次内的其它样本作为负样本；而对于正样本的构建，提出将同一文本两次通过带dropout的预训练语言模型生成正样本。相比其它无监督句嵌入方法，无监督SimCSE生成的句嵌入可以在使正样本彼此之间距离足够近的同时保留更多的语义信息，从而提高句嵌入的表征质量。无监督SimCSE的对比学习目标描述如下：

取句子集合 {xi}mi=1， 设hzi=fθ(xi，z)， 其中z是dro-pout的随机掩码(random mask)，hzi是xi在z下通过预训练语言模型h=fθ(x) 生成的向量表示，则无监督SimCSE的损失函数为

li=-logesim(hzii，hz′ii)/r∑Nj=1esim(hzii，hz′jj)/r

(1)

其中，z和z′是同一样本两次通过模型时的不同dropout掩码；sim(h1，h2) 是h1和h2的余弦相似度；N为训练批次内的句子数。

2.2 无监督SimCSE的改进方法SimCSE-PSER

由式(1)可知，无监督SimCSE仅通过dropout构造对比学习所需正样本，因此相同语义正样本的差异性有待提升；另外使用dropout本身会带来模型在训练与测试阶段训练目标的不一致性，从而增大模型参数自由度、降低模型泛化能力。因此本文提出SimCSE-PSER方法，通过BERT模型的dropout机制和位置嵌入扰动模块作为数据增强方式生成对比学习正样本，并结合之前仅在有监督领域应用的R-Drop正则化方法，旨在改善无监督SimCSE中以dropout机制作为数据增强方法的正则化效果并降低dropout本身带来的负面影响，从而达到提高模型泛化能力、提高无监督句嵌入表征质量的目的。

SimCSE-PSER分为两个主要部分：多扰动BERT句嵌入编码层和正则化对比损失层。SimCSE-PSER的整体架构如图1所示。

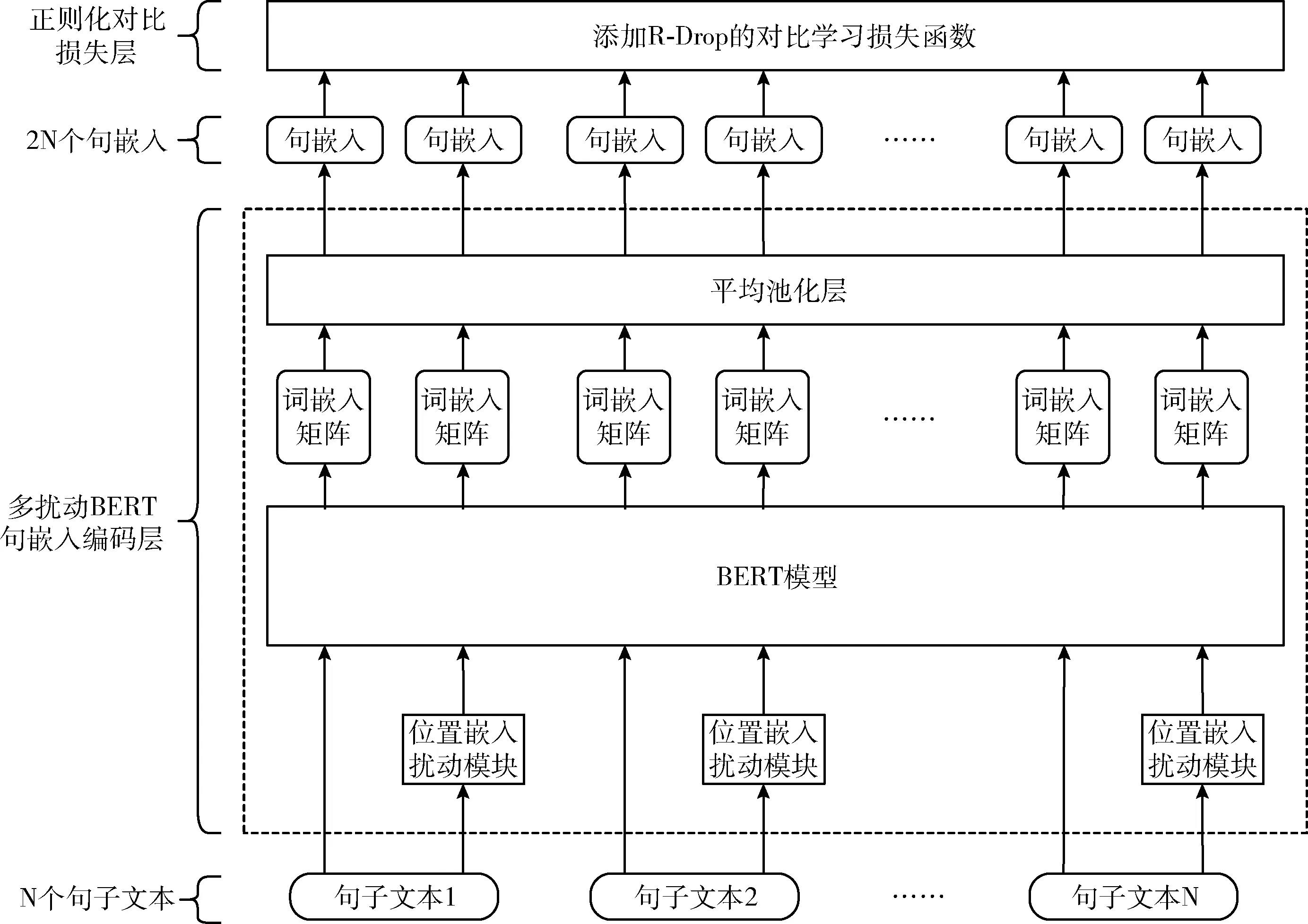
图1 SimCSE-PSER架构

2.2.1 多扰动BERT句嵌入编码层

在SimCSE-PSER中，同一句子文本将两次通过多扰动BERT句嵌入编码层：其中一次将直接输入带dropout的BERT模型，并在经过平均池化层后转换为对应句嵌入；另外一次将首先通过位置嵌入扰动模块再经过相同流程。

在BERT内部，句子文本的输入表征在嵌入层产生，其内容为词嵌入(token embedding)、段嵌入(segment embedding)、位置嵌入(position embedding)相加，如图2所示[1]。

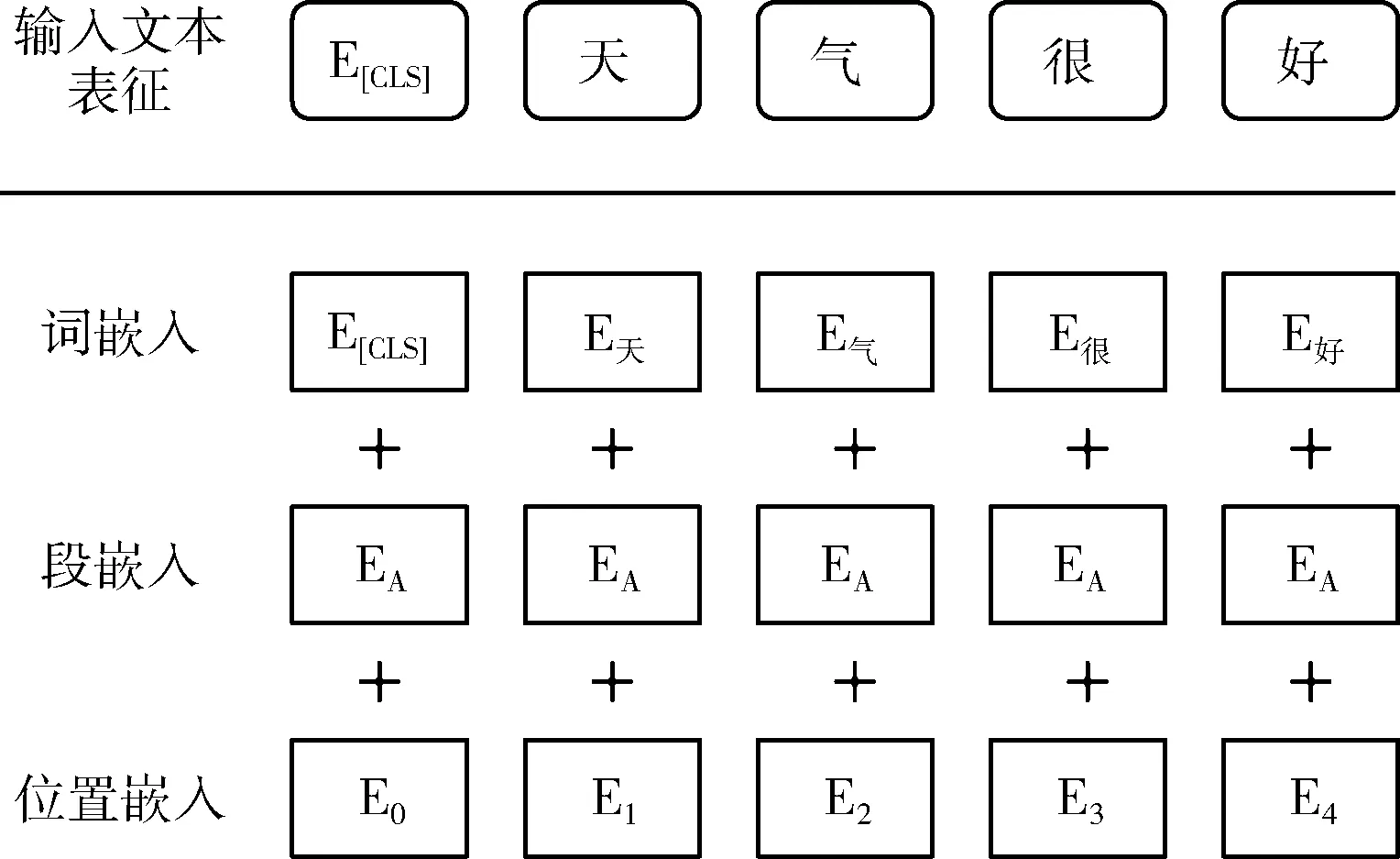
图2 BERT嵌入层

其中，词嵌入为输入句子文本中各个词的向量表示；段嵌入表示词所属的句子；位置嵌入根据模型指定的位置标识生成，包含每个词的顺序信息。三者相加后的句子输入表征将通过BERT的编码器部分，生成包含语义信息的词嵌入矩阵。

由于BERT基于注意力机制(attention mechanism)，对文本顺序不敏感，所以在BERT中模型对于文本顺序的感知全部依赖于位置嵌入。由此，SimCSE-PSER在构建对比学习的正样本时对两次输入BERT模型的句子文本中的其中一个句子进行随机乱序从而扰动位置嵌入，使BERT在另一文本顺序下感知文本，进而在尽量不损害文本语义的情况下提供额外的正样本变化。此时，位置嵌入扰动模块与BERT模型的dropout机制会联合生成句嵌入。

句子文本经过多扰动BERT句嵌入编码层的流程如下：对于句子文本数据集D=(xi)mi=1中的句子文本xi，分别经过带dropout的BERT模型和带dropout且加入位置嵌入扰动模块的BERT模型生成词嵌入矩阵ti、词嵌入矩阵t+i， 即ti=BERT1(xi，z)，t+i=BERT2(xi，z′)。 其中，ti，t+i∈L×D，z和z′分别代表BERT模型的dropout掩码，L代表句子长度，D代表词嵌入维数。之后，ti和t+i通过平均池化层生成句嵌入si、s+i。

2.2.2 正则化对比损失层

对于无监督SimCSE，dropout是其核心内容。作为一种正则化方法，dropout在模型训练时随机丢弃一部分的神经元以防止模型过拟合。然而，由于dropout丢弃神经元的操作，每次丢弃后被训练的模型都可以看作不同的子模型，因此使用dropout训练的模型具有参数自由度大、训练和测试阶段不一致等问题，影响dropout的正则化效果。为了避免无监督SimCSE中dropout机制带来的负面影响，本文在正则化对比损失层向损失函数引入R-Drop正则化方法，使si、s+i的分布尽量一致。

训练中，SimCSE-PSER每次迭代都会从句子文本数据集D中随机抽取N个句子文本组成训练批次，生成2N个句嵌入。这样，在一个训练批次中每个样本有1个正样本和N-1个负样本。与SimCSE相同，SimCSE-PSER采用Chen等[13]提出的对比损失，即使用交叉熵(cross entropy)作为基础损失函数[14]

L′i=-logexpsim(si，s+i)/r∑Nj=1expsim(si，s+j)/r

(2)

其中，sim为相似度函数，此处为余弦相似度；r为温度超参数。

对于每批训练样本，R-Drop(regularized dropout)[9]最小化两个dropout产生的不同子模型的输出分布之间的双向KL散度，使子模型之间输出分布一致，从而减少了使用dropout时模型在训练与测试阶段的不一致性。R-Drop之前仅在有监督领域应用，本文将其扩展引入无监督领域。R-Drop的描述如下：

给定训练数据集D=(xi，yi)ni=1， 训练目标为学习一个模型Pw(y|x)， 其中n为训练样本数，(xi，yi) 是标记的数据对，xi是输入数据，yi是标签。假设学习目标为最小化负对数似然(negative log-likelihood)损失函数，则对每个输入数据xi进行两次神经网络前向传播，从而获得模型预测的两个输出分布Pw1(yi|xi)、Pw2(yi|xi)。 此时负对数似然损失函数应为

LiNLL=-logPw1(yi|xi)-logPw2(yi|xi)

(3)

之后，R-Drop最小化两个输出分布之间的双向KL散度。设DKL(P1‖P2) 为P1、P2两个分布之间的KL散度，则

LiKL=12[DKL(Pw1(yi|xi)‖Pw2(yi|xi))+

DKL(Pw2(yi|xi)‖Pw1(yi|xi))]

(4)

设α为控制LiKL的权重超参数，则最终的损失函数为

Li=LiNLL+α·LiKL

(5)

在SimCSE-PSER中，R-Drop正则项应为

L″i=12[DKL(si‖s+i)+DKL(s+i‖si)]

(6)

最后，将式(2)和式(6)加权求和，最终的损失函数为

Li=L′i+α·L″i

(7)

其中，α为权重超参数。

3 实 验

3.1 数据集介绍

由于实验采用无监督方式，所以训练时仅使用各数据集的训练集部分的第一个句子文本。不使用第二句子文本的原因是：防止在采用批内负样本策略的对比学习方法上训练时抽取的同训练批次样本中出现语义相同样本，从而错误的在向量空间推开正样本。

3.2 评价指标

本文采用斯皮尔曼相关系数(Spearman’s rank correlation coefficient)作为语义文本相似度任务的评价指标，它将用于表示模型在数据集上对句子对的余弦相似度(cosine similarity)计算结果与数据集标签之间的相关性。对于数据集中一个句子对，模型生成对应的句嵌入对为(A，B)，则它们的余弦相似度为

cos(θ)=∑ni=1Ai×Bi∑ni=1(Ai)2×∑ni=1(Bi)2

(8)

其中，n为向量的维度。余弦相似度的值域为[-1，1]。

若X和Y分别为数据集文本对应的句嵌入表示之间的余弦相似度数列和对应标签的数列，则它们的斯皮尔曼相关系数为

ρs=1-6∑ni=1d2in(n2-1)

(9)

其中，di为Xi，Yi升序排序后的名次之差，即di=rg(Xi)-rg(Yi)。n为两组数据的数据对个数。

斯皮尔曼相关系数的值域为(-1，1]，等于0时代表两组数据没有相关性，越接近1代表两组数据越正相关，越接近-1代表两组数据越负相关。

3.3 参数设置

实验中的所有无监督句嵌入方法都将基于Google发布的中文BERT-Base模型，采用平均池化生成句嵌入。由于实验在中文领域进行，以下各无监督句嵌入方法的参数经过测试调整为在中文语义文本相似度任务中表现最佳的组合。本文实验中各无监督句嵌入方法参数设置见表1。

表1 各个无监督句嵌入学习方法的参数设置

由于Chinese-STS-B数据集样本数量偏少，训练轮数(epoch)将被设置为10，其它数据集的训练轮数设置为1。

3.4 实验结果与分析

本文表格中的数据皆为计算斯皮尔曼相关系数5次后取平均值。为了符合阅读习惯，表格中的斯皮尔曼相关系数都将乘以100表示，并省略小数点后两位的数字，最优数据将加粗表示。表2为SimCSE-PSER与其它无监督句嵌入学习方法的对比实验结果。

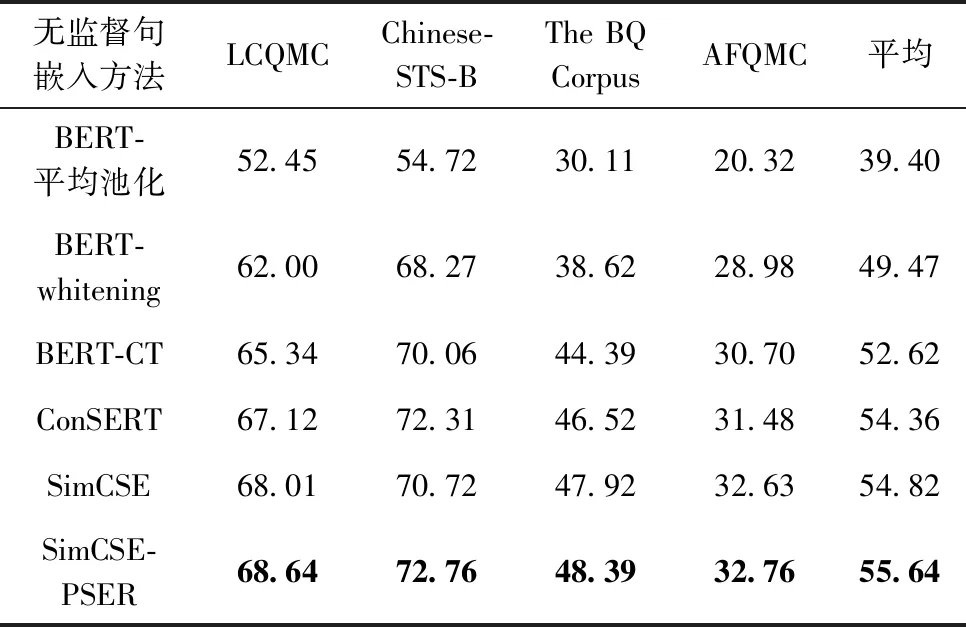
表2 SimCSE-PSER与其它无监督句嵌入学习方法的对比

根据实验结果可以看到：

(1)采用对比学习策略的BERT-CT、ConSERT、SimCSE和SimCSE-PSER在几个数据集上的表现都明显优于原始的无微调BERT和仅进行后处理的BERT-whitening。

(2)在采用对比学习策略的无监督句嵌入方法中，BERT-CT的表现略低于其它方法。这可能是因为其它对比学习方法采用的批内负样本策略比BERT-CT的负样本策略能提供更强的训练信号；而且BERT-CT采用两个独立的编码器，对于相同文本的表征可能造成较大的偏差。ConSERT、SimCSE和SimCSE-PSER都采用了单编码器结构和批内负样本策略，因此整体上结果优于BERT-CT。

(3)作为曾经在英文无监督语义文本相似度任务上表现最好的方法，SimCSE在中文任务上同样表现优异。在对比实验中，SimCSE取得了现有主流无监督句嵌入学习方法中最高的平均斯皮尔曼相关系数，验证了此方法在中文领域的有效性和泛用性。

(4)不管是在通用领域的数据集LCQMC、Chinese-STS-B上还是特定领域的数据集The BQ Corpus、AFQMC上，SimCSE-PSER相对于SimCSE均有提升。其中，SimCSE-PSER在通用领域的数据集LCQMC、Chinese-STS-B上相对于SimCSE提升较大，平均提升1.335；在银行金融领域的数据集The BQ Corpus、AFQMC上相对SimCSE提升较小，平均提升0.3。由于Google发布的中文BERT模型仅在中文维基语料上进行训练，未学习到银行金融领域的语义信息，所以可以推断：在模型已学习到语义信息的情况下，SimCSE-PSER能更好提升模型的句嵌入表征效果。

(5)相比于其它的无监督句嵌入方法，SimCSE-PSER在4个数据集上的斯皮尔曼相关系数均为最优，在Chinese-STS-B数据集上的结果最高达到了72.76。相比之前表现最好的方法SimCSE，SimCSE-PSER在单个数据集上最大提升了2.04，提升率约为2.9%；在4个数据集上平均提升了0.82，平均提升率约为1.5%，表明了改进策略的有效性。

3.5 消融实验

本节对所提方法进行了消融实验，以探究SimCSE-PSER各个组成部分的有效性。表3为对SimCSE-PSER中位置嵌入扰动和R-Drop两个部分的消融实验结果。

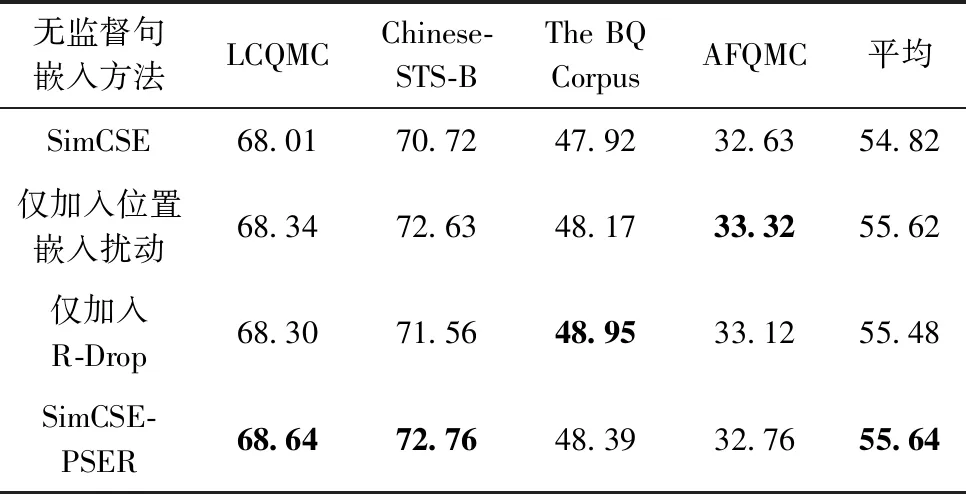
表3 SimCSE-PSER的消融实验

从表中结果可以看出：

(1)即使SimCSE在已经有dropout作为数据增强方法生成正样本时，单独加入位置嵌入扰动或R-Drop正则化方法后结果仍有提升。这表明SimCSE-PSER引入的位置嵌入扰动和R-Drop正则化方法可以有效弥补无监督SimCSE使用dropout作为数据增强手段在正样本构造方面和dropout本身的不足，提升了正则化效果，从而提高BERT模型在无监督情况下的句嵌入表征质量。

(2)对比位置嵌入扰动和R-Drop正则化方法，加入位置嵌入扰动在3个数据集上的结果优于仅加入R-Drop的情况。可见，加入位置嵌入扰动可以在不损害文本语义信息的情况下有效增强正样本多样性，进而提升原方法正则化效果；并且dropout作为数据增强手段在构造正样本方面的提升空间相对较大。

(3)SimCSE-PSER在4个数据集上的平均斯皮尔曼相关系数达到最优，并在通用数据集LCQMC、Chinese-STS-B上取得了最好结果，说明位置嵌入扰动和R-Drop正则化方法的结合能够更好地提升句嵌入的表征质量。

3.6 验证集上的评估曲线

本节主要对比采用批内负样本策略的对比学习方法，即SimCSE-PSER、SimCSE和ConSERT。图3为3种对比学习方法在LCQMC、Chinese-STS-B、The BQ Corpus、AFQMC这4个数据集上训练时验证集的评估曲线。

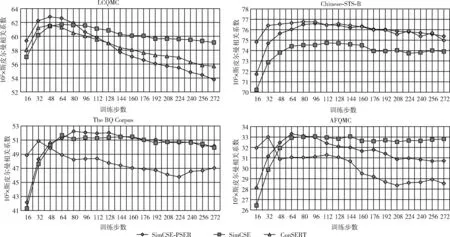
图3 3种学习方法在4个数据集上的评估曲线

可以看到，在4个数据集的验证集上采用批内负样本策略的3个对比学习方法都在较少的训练步数下达到最大斯皮尔曼相关系数，其中在LCQMC、The BQ Corpus、AFQMC的验证集上的SimCSE-PSER的最大斯皮尔曼相关系数大于其它两个方法。此结果表明，采用批内负样本策略的对比学习方法具有优秀的小样本学习能力，且本文方法SimCSE-PSER的小样本学习能力更强。因此对于实际生产环境中文本数据时常稀缺的情况，SimCSE-PSER具有更高的实际应用价值。

值得一提的是，在Chinese-STS-B的验证集上ConSERT的最大斯皮尔曼相关系数略微高于SimCSE-PSER和SimCSE，但是在测试集上的结果却高于SimCSE且低于SimCSE-PSER。可见，SimCSE-PSER加入的改进带来了更好的正则化效果，因此相比其它两种方法防过拟合能力更强，拥有更强的泛化能力。

从图中还可看出，采用批内负样本策略的对比学习方法过度训练后会使句嵌入表征效果下降。这可能是采用批内负样本策略的对比学习训练目标造成的：在向量空间中拉近各样本与正样本之间的距离，推远与批内负样本之间的距离。这样，过强的负样本信号可能会使向量空间中样本的分布变为群间稀疏、群内密集的集群，降低模型的句嵌入表征能力。因此，该类方法训练步数不宜过高，这也进一步说明SimCSE-PSER方法可以在取得良好性能的同时，具有较高的训练效率。

4 结束语

本文针对无监督SimCSE使用dropout作为数据增强方法的不足提出了一种基于改进SimCSE的无监督句嵌入方法SimCSE-PSER。该方法使用BERT模型的dropout机制与位置嵌入扰动模块作为数据增强方法联合构造对比学习所需的正样本，弥补相同语义正样本差异性的不足；同时结合R-Drop正则化方法，降低无监督SimCSE中dropout机制带来的负面影响。实验结果表明，SimCSE-PSER相比其它主流无监督句嵌入方法在跨领域的多个数据集上都展现出更强的句嵌入表征能力。下一步的工作重点将放在提高对比学习中的负样本质量。