基于双移动锚节点的无线传感器网络定位算法
2023-09-13崔焕庆赵君宜罗汉江
崔焕庆,赵君宜,罗汉江
(山东科技大学 计算机科学与工程学院,山东 青岛 266590)
0 引 言
本文主要针对移动锚节点辅助定位算法进行研究。目前,已经有学者对相关算法进行了研究。SLMAT[1],H-Curves[2]和M-Curves[3]均使用单个锚节点扫描部署区域。∑-SCAN[4]对Z-Curves和SCAN进行了改进,提高了定位精度。SSD[5]通过减少虚拟锚节点来节省能耗。GSCAN[6]、GTURN和PP-MMAN[7]均使用3个移动锚节点,并使虚拟锚节点成等边三角形分布,提高了定位精度。其中,GSCAN的虚拟锚节点数量较多,而GTURN的路径较长。文献[8,9]设计路径的目的均为减少共线锚节点的数量,提高定位精度。
目前,元启发式优化算法已经非常普遍,并且也广泛应用于无线传感器网络定位中的未知节点位置估计。MGDV-Hop[10]利用混合策略对萤火虫群优化算法进行了改进,提高未知节点的定位精度。文献[11]使用粒子群优化算法(particle swarm optimization,PSO)来估计未知节点的位置。文献[12]采用鲸鱼优化算法对接收信号强度与信号传输距离之间的关系公式进行优化,降低了测量误差。文献[13]提出了一种新的非视距的定位算法,并通过改进的粒子群优化算法估算目标的位置。文献[14]使用改进的灰狼优化算法估计未知节点的坐标。文献[15]将改进樽海鞘群算与DV-Hop结合,提高了定位精度。
本文的主要贡献有:
(1)设计了一种双移动锚节点协作的路径规划算法DASCAN(Dual-Anchor SCAN),缩短了路径长度并且使用较少的虚拟锚节点,降低了能耗。
(2)使用加权质心算法和鲸鱼优化算法估算未知节点的坐标,提高了定位精度。
1 系统模型
在无线传感器网络中,已知自身位置的节点称为锚节点,其它节点称为未知节点,锚节点分为静态锚节点和移动锚节,后者在移动过程中需定期广播自身位置等信息。锚节点广播的这些信息称为虚拟锚节点。假设无线传感器网络由NU个部署在高H、宽L的矩形区域内的未知节点组成。第i个节点Ui的真实坐标为(xi,yi),利用定位算法求得的估计坐标为 (i,i)。 两个移动锚节点分别记为MA1、MA2,它们广播的虚拟锚节点信息包含实时位置和发送信号强度两个字段。
在RSSI测距中,无线信号在传播过程中强度会随着距离的增加而降低,并且会受到环境因素的影响。通常假设在理想的自由空间中,RSSI与发送器和接收器之间的距离的平方成反比。令Pr(d)表示在距离d处的接收功率,其值遵循弗里斯方程
Pr(d)=(λ4πd)2PtGtGr
(1)
其中,Pt是发射功率,Gt和Gr分别是发射和接收天线的天线增益,λ是发射器信号的波长(以米为单位)。
但实际上,一些因素(例如阴影和反射)可能会影响无线电信号的传播以及接收功率,因素取决于环境并且是不可预测的。由于无法精确跟踪阴影效果,因此通常将其建模为对数正态分布的随机变量。考虑到随机性,信号强度根据幂定律随距离而减小。一种用于无线电的模型如式(2)所示
Pr(d)=P0(d0)-η10log10(dd0)+Xσ
(2)
其中,P0(d0) 表示在某个参考距离d0处的接收功率,η表示路径损耗指数,Xσ表示对数正态随机变量,其方差为σ2。通过该模型,距离d的最大似然估计如式(3)所示
d^=d0(PrP0(d0))(-1/|η)
(3)
假设锚节点与未知节点的通信范围是一个半径为R的圆。实际应用中,传感器节点的信号传播容易受周围环境的影响,通信范围不是一个规则的圆,所以将通信信号不规则度(degree of irregularity,DOI)加入到无线通信传播模型中。DOI表征了无线电射程受多径、阴影等衰弱影响而导致的传输范围的各向异性,数值越高表示传输范围受环境影响越严重,其定义如式(4)所示

(4)
其中,Ki是第i个方向上的不规则度,Rand是在[0,1]内服从均匀分布的随机数,N是正整数集合。
使用定位算法定位的未知节点个数占未知节点总数的比例称为定位率LR,即
LR=NldNU
(5)
其中,Nld表示被定位节点的个数。平均定位误差e为
e=1Nld∑Nldi=1(xi-i)2+(yi-i)2
(6)
2 本文算法
2.1 锚节点路径规划算法
为了更合理地部署虚拟锚节点,先将监视区域进行网格状划分。纵向上等间距划分为n+1行,并从下向上依次编号为第0、1、2、……、n行,相邻两行之间的间距为h,即每个单元格的高为h。横向上等间距划分m+1列,从左向右依次编号为第0、1、2、……、m列,相邻两列之间的间距为d,即每个单元格的宽为d,网格划分和虚拟锚节点部署结果如图1所示。
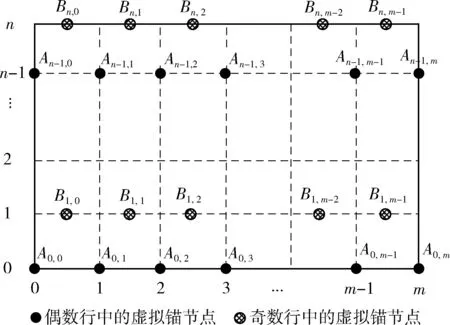
图1 部署区域划分及虚拟锚节点位置
DASCAN要求奇数行和偶数行采用不同的部署方式。在图1中,偶数行和奇数行的虚拟锚节点分别用A和B表示。 ΔAi,jAi,j+1Bi+1,j和ΔAi,jAi,j+1Bi-1,j是等边三角形。因此,h=32d。 以左下角为坐标原点(0,0),第i行的虚拟锚节点坐标为:
(1)i≤n且为偶数时,Ai,j=(j×d,i×h), 其中j=0,1,2,…,m。
(2)i≤n且为奇数时,Bi,k=((k+12)×d,i×h), 其中k=0,1,2,…,m-1。
如果仅用一个移动锚节点,则需要交替遍历偶数行和奇数行,路径较长。所以DASCAN采用两个移动锚节点以分别遍历偶数行和奇数行的虚拟锚节点。算法1给出了DASCAN算法。
算法1:路径规划算法
输入:H、L、h、d。
输出:MA1、MA2的移动路径
(1) Put MA1and MA2inA0,0andB0,0
(2) SetList1←Φ,List2←Φ
(3)flag←1,i←0,j←1,k←0
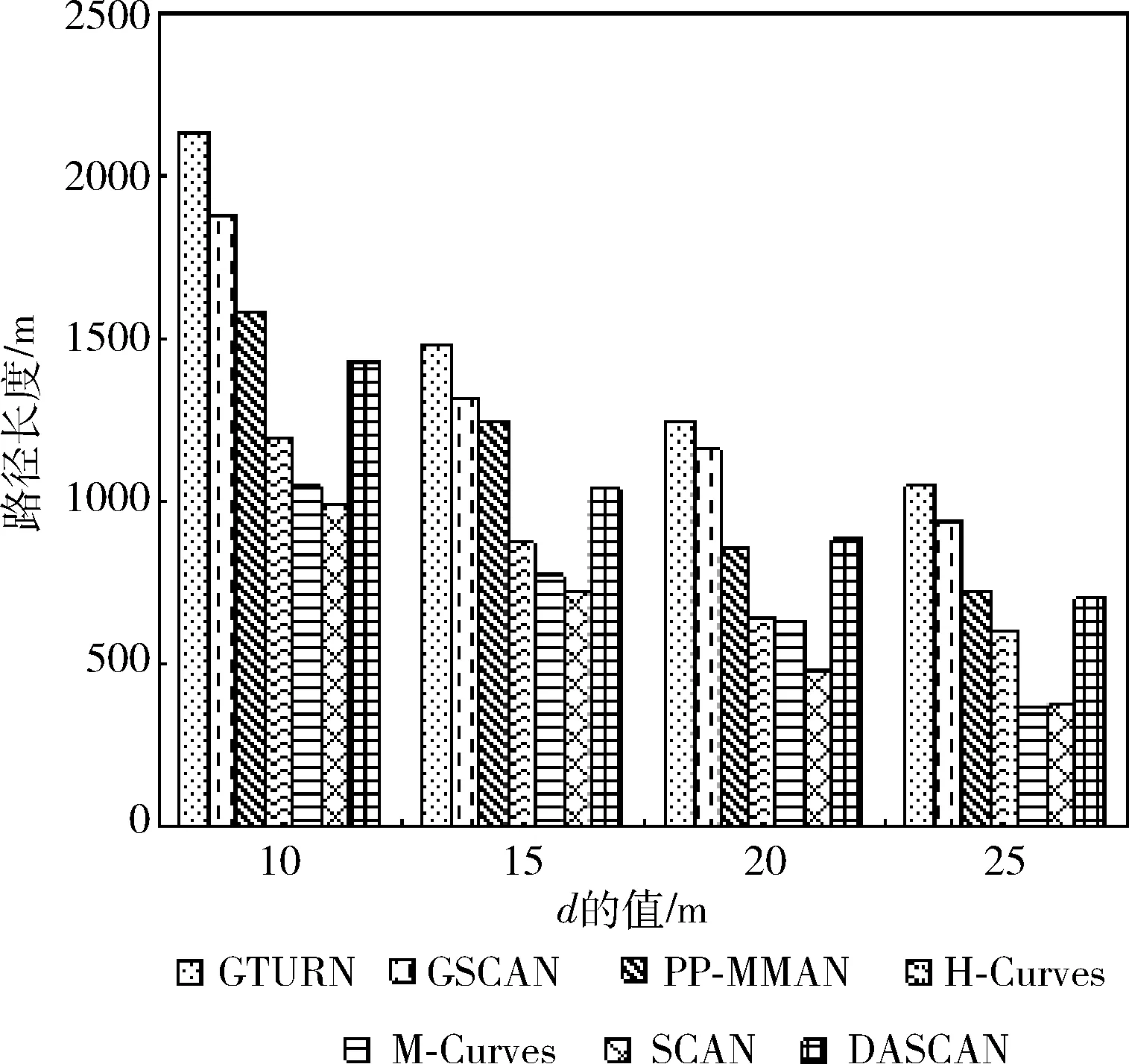
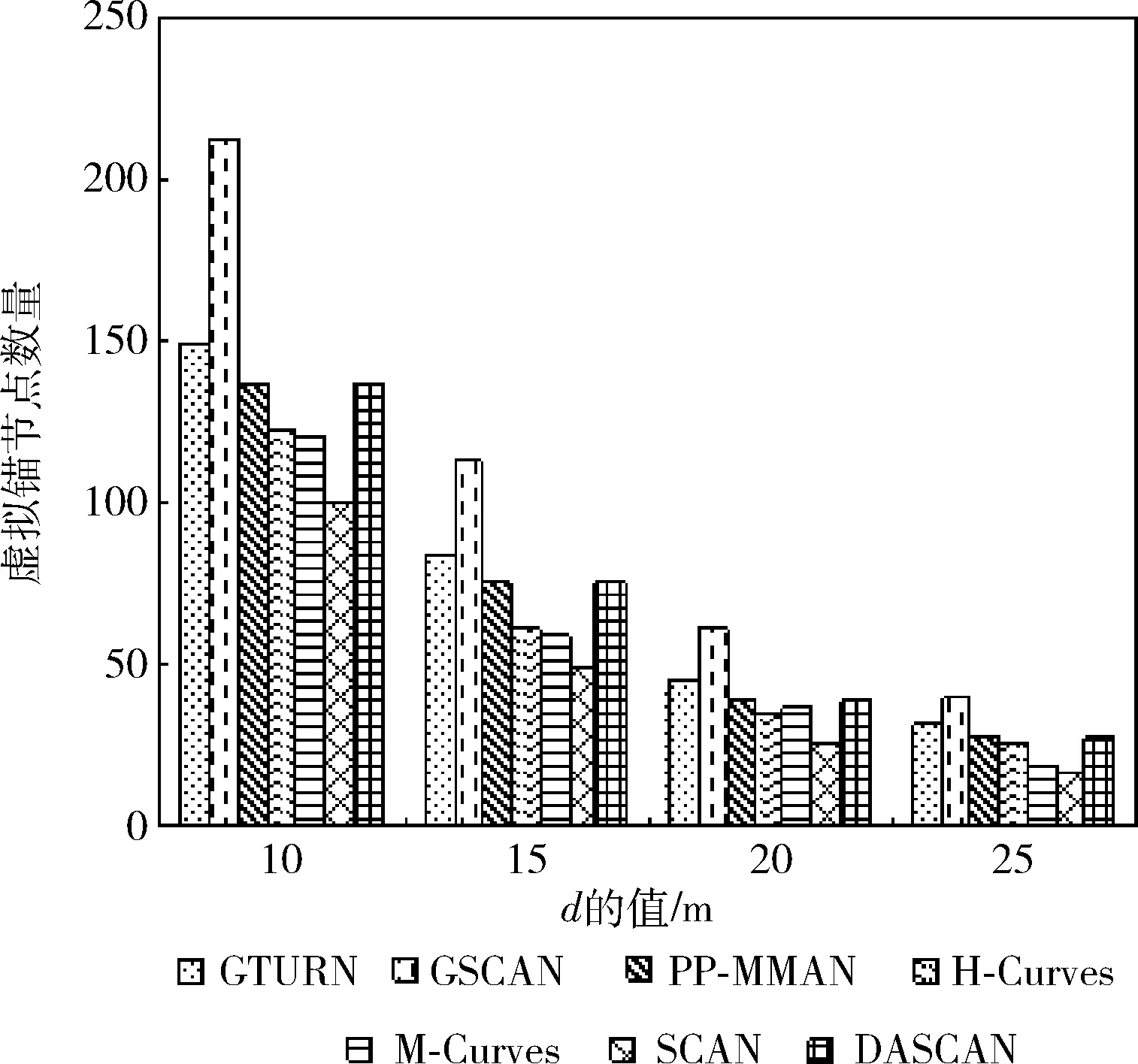
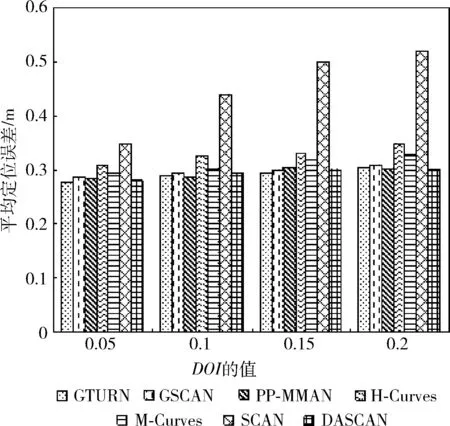
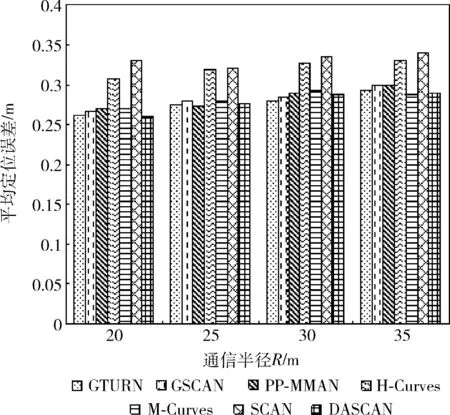
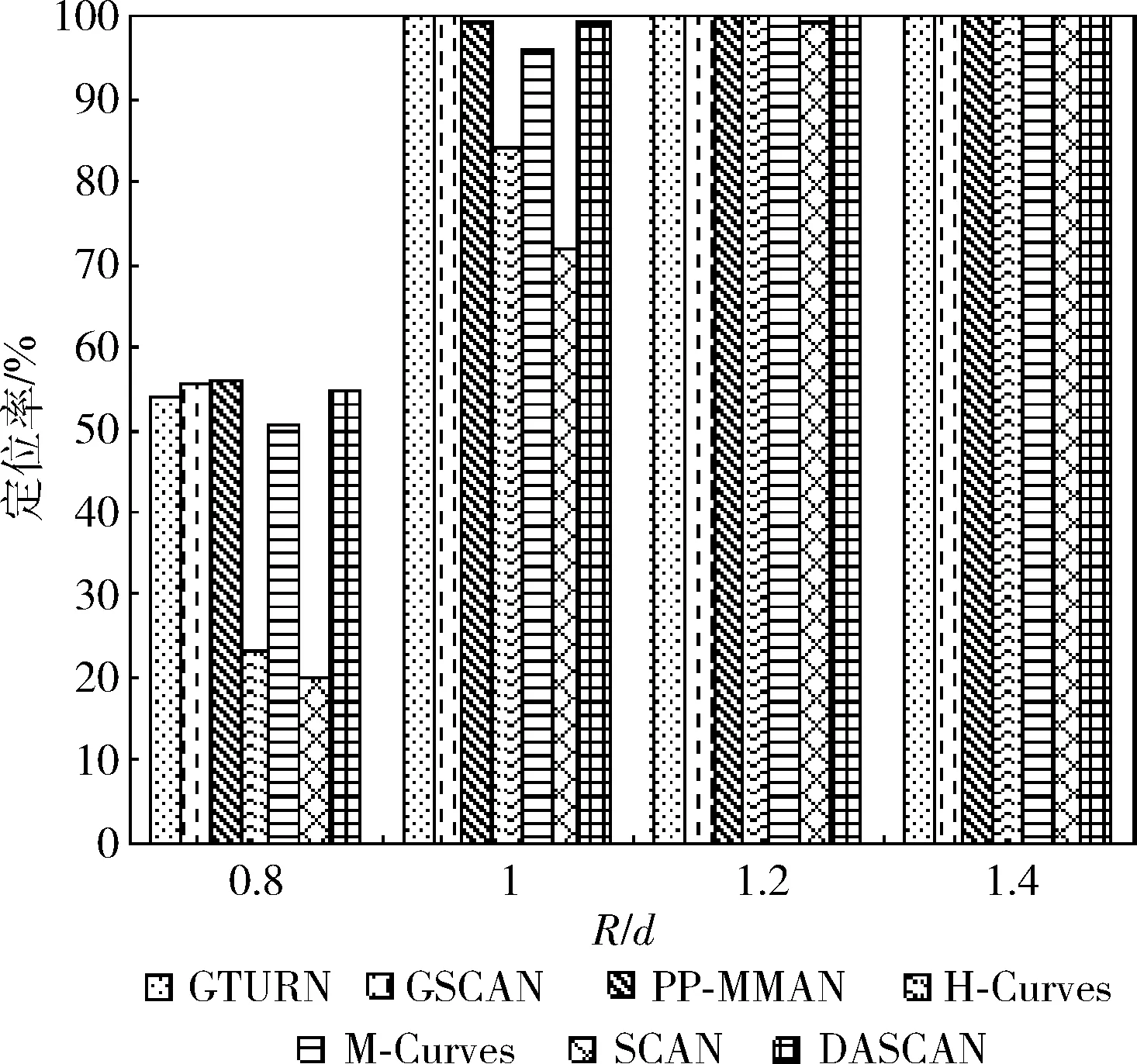
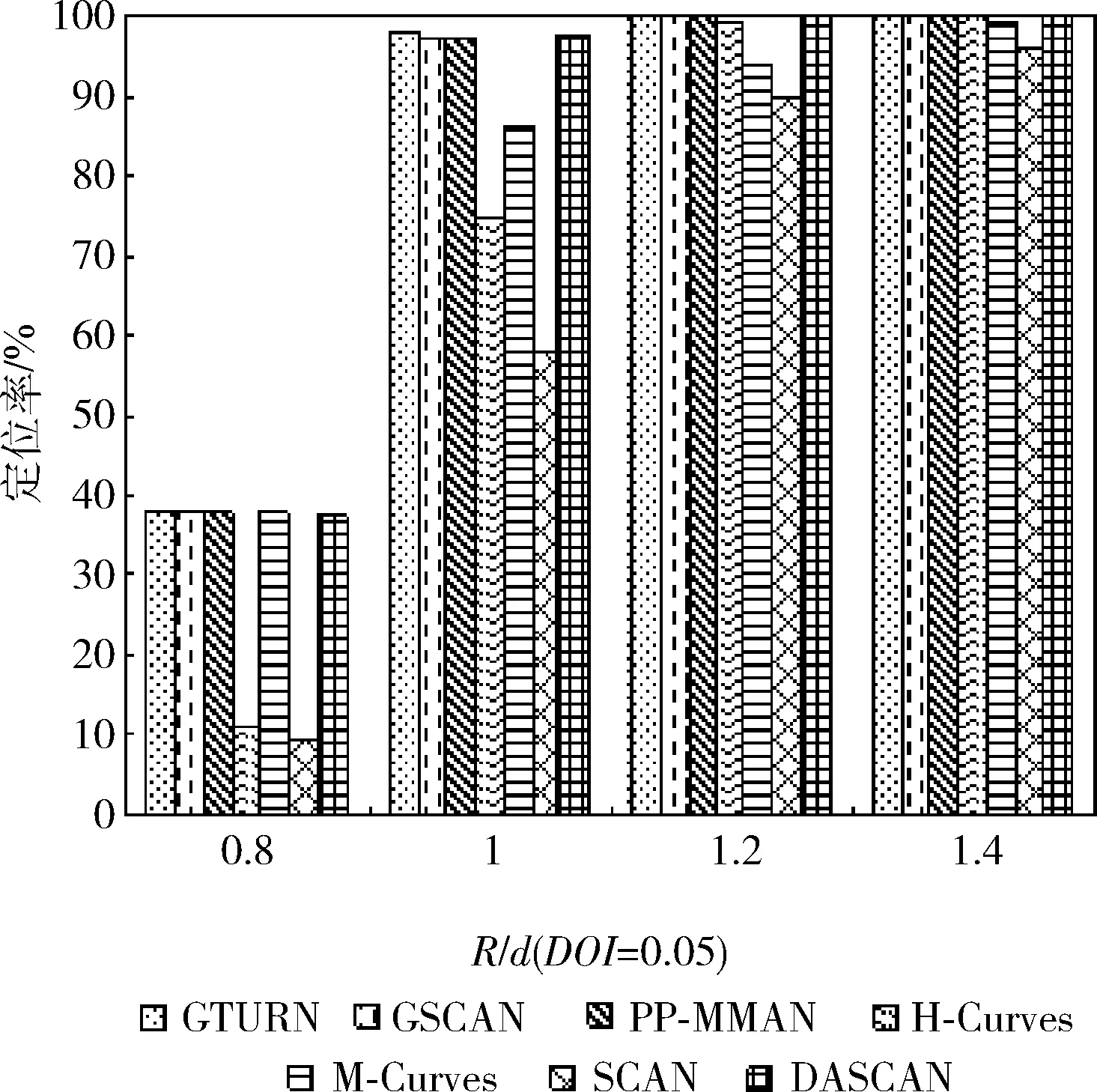
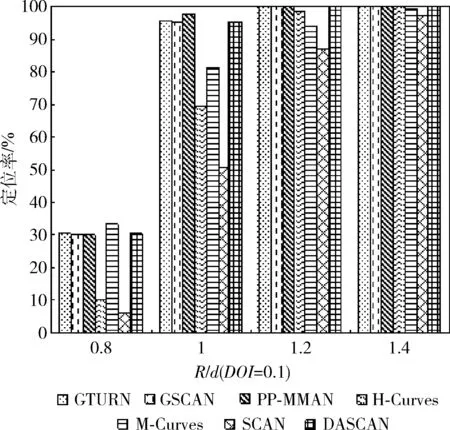
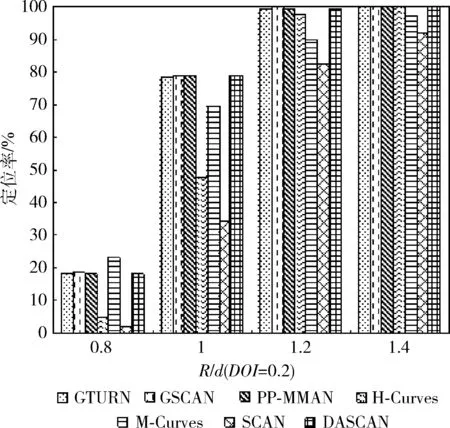
(4)whilei (5)ifflag=1 (6)List1←List1∪{Ai,0,Ai,1,…,Ai,m} (7)List2←List2∪{Bi+1,0,Bi+1,1,…,Bi+1,m-1} (8)flag←2 (9)elseifflag=2 (10)List1←List1∪{Ai,m,Ai,m-1,…,Ai,0} (11)List2←List2∪{Bi+1,m-1,Bi+1,m-2,…,Bi+1,0} (12)flag←1 (13)endif (14)i←i+2 (15)endwhile (16)ifn%2=0 &&flag=1 (17)List1←List1∪{An,0,An,1,…,An,m} (18)elseifn%2=0 &&flag=2 (19)List1←List1∪{An,m,An,m-1,…,An,0} (20)endif 算法1中,List1、List2分别用来储存MA1、MA2遍历的虚拟锚节点列表。第(1)~第(3)行初始化各变量,第(4)~第(15)行计算List1和List2,其中flag=1表示锚节点从左向右移动(第(5)~第(8)行),flag=2表示锚节点从右向左移动(第(9)~第(13)行)。当n为偶数时,MA1需要额外遍历最后一行,移动方向取决于此时flag的值(第(16)~第(20)行)。 算法1生成的4种移动路径如图2所示,其中“flag值”是指执行到第(16)行时flag的值。算法1执行结束后,MA1和MA2分别沿List1、List2遍历整个部署区域,并在指定虚拟锚节点处广播信息。 图2 算法1产生的4种不同路径 鲸鱼智能优化算法是2016年由澳大利亚格里菲斯大学的Mirjalili等提出的一种新的群体智能优化算法,该算法具有实现简单、参数少以及不易陷入局部最优等优点。 在鲸鱼优化算法中,每个鲸鱼被看作是一个可行解。鲸鱼在狩猎时,会沿着“9”字形或者圆形路径吐出气泡包围猎物,这种狩猎行为称为bubble-net捕食策略。该算法包括环绕猎物、螺旋泡泡网猎食以及搜索猎物3个阶段。 在狩猎阶段,WOA假设当前算法的最优解为目标猎物,其它鲸鱼个体会向着当前适应度值最佳的鲸鱼的位置移动,该行为的数学模型如下所示 D=|C·X*(t)-X(t)| (7) X(t+1)=X*(t)-A·D (8) A=2a·r1-a (9) C=2·r2 (10) 其中,t为当前迭代次数;A和C是协同系数向量;X*表示当前最优的鲸鱼的位置向量;X(t)表示鲸鱼当前的位置向量;在整个迭代过程中,a由2线性降到0;r1和r2是[0,1]中的随机向量。C为[0,2]内的随机值构成的向量,此系数提供了随机权重,以避免算法陷入局部最优。 鲸鱼在猎食的过程中会进行两种不同的行为来包围猎物,分别是缩小包围圈和沿螺旋状路径吐气泡驱赶猎物,每只鲸鱼选择这两种该行为的概率是相等的。数学模型如式(11)所示 (11) 其中,b为常数,l和p为均匀分布在[-1,1]中的随机数。 随着迭代的进行,a的值会从2线性减小到0,a的值的变化会引起A的变化,当 |A|<1时,鲸鱼会向最优个体移动,当 |A|>1时,鲸鱼会随机移动。鲸鱼随机移动的数学模型如式(12)和式(13)所示 D=|C·Xrand(t)-X(t)| (12) X(t+1)=Xrand(t)-A·D (13) 其中,Xrand是随机选择的鲸鱼位置向量,通过此方式可以让WOA进行全局搜索,避免陷入局部最优。 在定位阶段,使用加权质心和鲸鱼优化算法估算未知节点坐标,具体步骤如下。 结合所设计的路径,先使用加权质心算法来估算未知节点位置。假设移动锚节点在部署区域内产生的虚拟锚节点的数量为NV,未知节点Ui(i=1,…,Nu) 维护一个虚拟锚节点列表Li,如果Ui接收到虚拟锚节点Vj的信标信息,则将Vj的坐标 (xj,yj)、 信号强度RSSIi,j以及根据RSSI测距模型计算得到的估计距离dei,j添加至Li中。将所有的虚拟锚节点按RSSIi,j值排成递减序,选择虚拟锚节点V1、V2、V3的方法为: (1)选择Li中前两个最大RSSIi,j对应的虚拟锚节点作为V1、V2,在Li中从前往后依次查找可与V1、V2构成边长为d的等边三角形的虚拟锚节点Vk(k>2)作为V3。 (2)如果利用步骤(1)不能找到满足此条件的V3,则选择剩余虚拟锚节点中最大RSSIi,j对应的虚拟锚节点作为V3。 未知节点Ui在选择V1、V2、V3后,使用加权质心算法估计未知节点Ui的位置 (′i,′i)=∑3j=1ωj×(xj,yj)∑3j=1ωj (14) 其中,ωj=RSSIj为加权因子,第i个节点的定位误差为ei,WCL=(xi-′i)2+(yi-′i)2。 找出所有可定位节点的定位误差中的最大值,记为emax。 根据使用加权质心得到的Ui的估算坐标 (′i,′i) 和最大定位误差emax确定对应的WOA算法搜索空间SPi,即:[′i-emax,′i+emax]×[′i-emax,′i+emax], 如图3所示。 图3 根据质心确定搜索空间SPi 在二维的无线传感器网络中,第i个未知节点与第j个虚拟锚节点估计距离的平均误差定义如下 ei,j=|(xi-xj)2+(yi-yj)2-dei,j| (15) 其中,(xj,yj) 为虚拟锚节点Vj的坐标,(xi,yi) 为传感器节点Ui的实际位置,dei,j为虚拟锚节点Vj与传感器节点Ui的测量距离。通过这种方法,我们可以得到如下的目标函数 minf(x,y)=1Ni∑Nij=1|(x-xj)2+(y-yj)2-dei,j| (16) 其中,Ni是传感器节点Ui可以接收到的信标信息数。 最后,在SPi中随机产生鲸鱼种群,使用以上目标函数估算Ui的最终坐标。算法2给出了计算第i个传感器节点坐标Ui的过程。 算法2:节点位置估算算法 输入:Li,MaxIter (1)SortLiin descending order according toRSSIi,j (2)ifdist(Li(1),Li(2))=dist(Li(1),Li(k))=dist(Li(2),Li(k))=d (3)V1←Li(1);V2←Li(2);V3←Li(k) (4)else (5)V1←Li(1);V2←Li(2);V3←Li(3) (6)endif (8)Calculate localization error of each node and findemax (9)SPi←[′i-emax,′i+emax]×[′i-emax,′i+emax] (10)Initialize whales populationXi(i=1,2,…,n) inSPi (11)Calculate fitness of each whale using Eq.(16) (12)X*←the best search agent (13)while(t (14)foreach whale (15) Updatea,A,C,l, andp (16)ifp<0.5 (17)if|A|<1 (18) Update current whale by Eq.(11)(p<0.5) (19)elseif|A|>1 (20) Select a random whale (Xrand) (21) Update current whale by Eq.(13) (22)endif (23)elseifp>0.5 (24) Update current whale by the Eq.(11) (25)endif (26)endfor (27) Check if any whale goes beyond theSPiand amend it (28) Calculate fitness of each whale (29) UpdateX*if there is a better solution (30)t←t+1 (31)endwhile (32)returnX* 算法2中的第(1)~第(6)行根据Ui找到对应的V1、V2、V3。第(7)~第(9)根据式(14)得到 (′i,′i), 然后计算每个未知节点的定位误差并找到最大值emax。最后根据 (′i,′i) 和emax确定出对应的搜索空间SPi,限制WOA的初始化区域,加快算法收敛速度。第(10)~第(12)行在SPi中初始化鲸鱼的位置,使用式(16)计算每一个个体的适应度值,找出适应度最好的个体记为X*。第(13)~第(31)行是鲸鱼优化算法的执行过程,MaxIter为最大迭代次数。先更新a、A、C、l和p的值,当p<0.5且 |A|<1时,鲸鱼群向最优鲸鱼位置移动,使用式(11)更新每只鲸鱼的位置。当p<0.5且 |A|>1时,鲸鱼群随机移动,使用式(13)更新每只鲸鱼的位置。当p>0.5时,鲸鱼沿螺旋状路径吐出气泡包围猎物,使用式(11)更新每只鲸鱼的位置。修正超出搜索空间SPi的鲸鱼个体。使用式(16)更新每只鲸鱼的适应度值,并更新X*的值。在迭代循环结束前重复执行以上步骤。第(32)行返回X*的值即为 (i,i)。 使用MATLAB 2016a进行仿真实验。部署区域为100 m×100 m的正方形二维区域,对SCAN[1]、GTURN[7]、GSCAN[7]、PP-MMAN[4]、H-Curves[2]、M-Curves[3]以及本文提出的DASCAN在路径长度、定位精度和定位率方面进行对比。 d取值为10 m、15 m、20 m、25 m。实验结果如图4所示。可以看出,d相同时,GTURN和GSCAN都是最长的,原因在于它们使用3个移动锚节点,并且GSCAN存在重复路径。H-Curves、SCAN和M-Curves由于只有一个移动锚节点,并且路径结构较为简单,所以移动路径较短。DASCAN短于PP-MMAN,比最长的GTURN路径平均缩短了44%,比最短的SCAN路径平均长了26.5%。 图4 路径长度比较 下面对不同路径规划算法的虚拟锚节点数目进行对比。实验结果如图5所示,7种路径规划算法的虚拟锚节点的平均数量排序为GSCAN>GTURN>PP-MMAN=DASCAN>H-Curves>M-Curves>SCAN。GSCAN的虚拟锚节点数量是最多的,这是因为GSCAN的移动锚节点会在某些位置重复广播信标信息。DASCAN产生的虚拟锚节点数目均少于GSCAN、GTURN、PP-MMAN以及M-Curves,但是比起H-Curves和SCAN要更多。因为在相同d的情况下,DASCAN的路径相邻两行之间的距离比SCAN和H-curve更小,所以在部署区域均为100 m2的情况下,DASCAN会产生更多的虚拟锚节点。虽然M-Curves的虚拟锚节点更密集,但是该算法不需要在部署区域边界生成虚拟锚节点。从图中可以看出,本算法产生的虚拟锚节点数目相比GSCAN平均减少了53%,相比SCAN平均增加了32%。 图5 虚拟锚节点数量比较 综合路径长度以及虚拟锚节点数量,分别计算7种路径规划算法产生的总能耗。实验结果如图6所示,7种路径规划算法的能耗从高到低为GTURN、GSCAN、PP-MMAN、DASCAN、H-Curves、M-Curves、SCAN。由于GSCAN和GTURN的虚拟锚节点数量较多,路径较长,所以这两种算法的能耗比其它算法更高,由于DASCAN的路径长度比PP-MMAN更短,所以能耗相对更低。H-Curves、M-Curves和SCAN的虚拟锚节点数量较少,路径较短,产生的能耗也更低。本文算法相比能耗最高的GTURN能耗平均降低了42.7%,相比能耗最低的SCAN能耗平均增加了35.4%。 图6 能耗比较 取R=15 m,DOI=0,实验结果如图7所示。可以看出,无论使用哪一种路径规划算法,使用加权质心算法计算得到的结果误差最大,而使用WOA得到的结果误差最小。在使用加权质心定位未知节点时,H-Curves、M-Curves 和SCAN的定位误差要远远高于其它路径规划算法,当使用三边定位时,所有路径规划算法的定位误差大幅降低,H-Curves、M-Curves和SCAN的定位误差仍略高于其它路径规划算法。在使用PSO和WOA定位节点时,所有路径规划算法的定位误差进一步下降,并且WOA的平均定位误差略低于PSO,此时H-Curves和SCAN的定位误差仍要高于其它算法。 将所有路径与WOA算法联合来对比性能。实验结果如图8所示。从图中可以看出,随着DOI的增加,每个未知节点接收到的广播信息数量减少,每种路径规划算法的定位误差均受到了DOI的影响,但影响幅度有所差别。由于SCAN和H-Curves存在大量的共线虚拟锚节点,所以定位误差相比其它路径更大,而且更容易受DOI的影响。而DASCAN和其余的路径受DOI影响相对较小。 图8 路径在不同DOI下的定位精度 最后不考虑DOI的影响,比较每种路径在不同的通信半径R下的定位精度。实验结果如图9所示。可以看出,当d=15 m时,每种路径的平均定位误差均随着通信半径R的增大而增加。虽然通信半径越大,每个未知节点接收到的信标信息越多,但是由于RSSI的缺陷,未知节点与距离较远的虚拟锚节点之间的测距误差较大。所以当通信半径增大时,定位误差会变大。H-Curves和SCAN在不同R下的定位误差均高于其它定位算法,DASCAN的定位误差以及受通信半径的影响较小。 图9 路径在不同通信半径下的定位精度 取d=15 m,R取0.8d、1.0d、1.2d、1.4d,DOI=0、0.05、0.1、0.15、0.2。实验结果如图10所示。 图10 路径在不同通信半径下的定位率 整体来看,每种路径的定位率随着Rd的增大而增大。在每种取值的情况下,DASCAN、GTURN、GSCAN和PP-MMAN的定位率十分接近,其余路径的定位率从高到低依次为M-Curves、H-Curves、SCAN。当R=0.8d时,7种路径的定位率差距最大,此时DASCAN、GTURN、GSCAN和PP-MMAN的定位率约为50%,H-Curves和SCAN仅能定位20%左右的未知节点。当R=1.4d时,7种路径均可定位所有未知节点。 最后,比较了在不同DOI、R对定位率的影响,实验结果如图11、图12、图13和图14所示。整体来看,每种DOI取值下,每种路径的定位率随着Rd的增大而增大。每种取值情况下,DASCAN、GSCAN、GTURN和PP-MMAN的定位率都十分接近,均高于H-Curves、M-Curves、SCAN的定位率。DASCAN、GSCAN、GTURN、PP-MMAN的定位率接近,高于其它路径。整体来看,DASCAN的定位率比M-Curves、H-Curves、SCAN分别平均高出3%、15%、19%。R=0.8d,DOI=0.2时,7种路径的平均定位率最低,此时DASCAN的定位率约30%,H-Curves和SCAN的定位率低于10%。R=1.4d,DOI=0.05时,7种路径的定位率均为100%。当R=d,DOI=0.2时,DASCAN的定位率相比其它路径平均提升最大,为30%;R=d,DOI=0.05时,DASCAN的定位率相比其它路径平均提升最小,为20%。 图11 路径在不同通信半径下的定位率(DOI=0.05) 图12 路径在不同通信半径下的定位率(DOI=0.1) 图13 路径在不同通信半径下的定位率(DOI=0.15) 图14 路径在不同通信半径下的定位率(DOI=0.2) 综上,DASCAN比GTURN、GSCAN、PP-MMAN路径短,避免了重复广播信息,从而降低了移动锚节点的能耗。同时,比H-Curves、M-Curves和SCAN有更高的定位率和定位精度,配合WOA可以进一步提高算法的定位精度。 本文提出了一种基于双移动锚节点和鲸鱼优化的无线传感器网络定位算法,设计了一种双移动锚节点路径,并使用加权质心算法辅助鲸鱼优化算法估算未知节点的坐标,提高了定位精度。实验结果表明,DASCAN比其它采用多个移动锚节点的路径更短,定位误差更小,比H-Curves等采用单个移动锚节点的定位率、定位精度更高,并且受DOI和RSSI测距误差的影响更小。 但是,本文所提出的算法在部署区域的边缘位置的定位精度较低,下一步需提出用于区域边缘未知节点定位的补偿算法。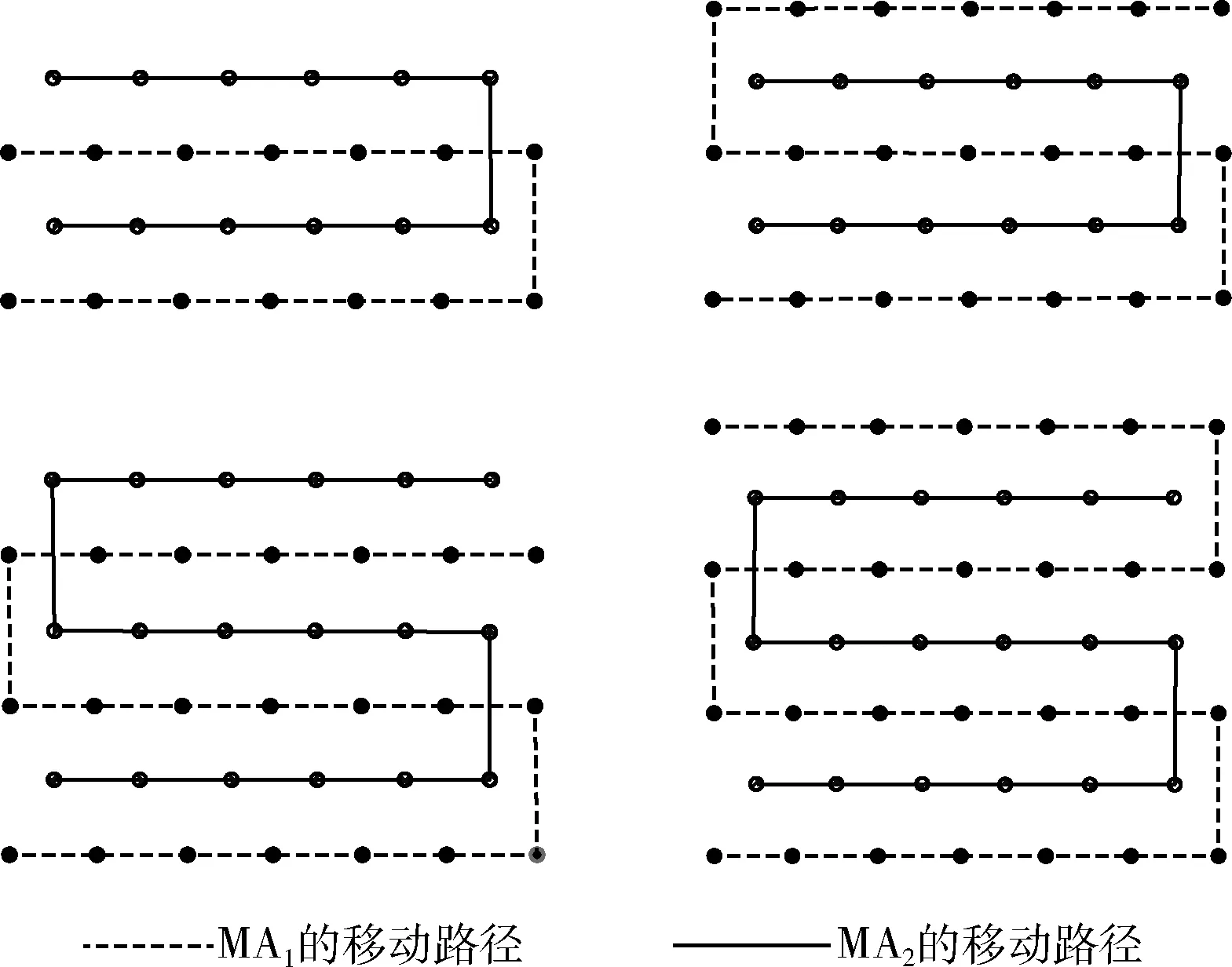
2.2 鲸鱼优化算法
2.3 节点位置估算算法

3 仿真实验
3.1 路径对比

3.2 定位精度对比
3.3 定位率对比

4 结束语
