基于binAD算法的边缘计算卸载决策

王 泽，郭荣佐

(四川师范大学 计算机科学学院，四川 成都 610101)

0 引 言

随着物联网的出现和移动终端设备的普及，诸多物联网应用正在影响和改变着生活，例如图像识别、车联网、虚拟现实、智能家居等[1-4]。计算这些应用程序内存占用率高、能耗高、计算资源需求大，且对及时性要求严格。尽管目前移动终端设备的处理器、电池容量和其它软硬件持续更新换代，但是对于单个设备来说，物理设计仍受限，无法处理计算密集型和时间敏感型应用程序。

计算卸载技术[5]可以解决上述问题，将计算密集型或时间敏感型应用程序任务卸载到其它服务器端执行。以移动云计算[6](MCC)为例，用户端的移动终端设备将计算任务卸载到云服务器上执行计算，以此可以解决移动终端设备算力、电池、内存不足等问题。目前大量的移动终端设备、工业物联网设备都需要云计算服务，而云计算存在传输时延大、带宽不足、数据隐私泄漏等缺点。边缘计算[7](EC)在靠近移动终端设备的无线接入网络边缘部署分布式计算和缓存资源。与MCC相比，EC的计算能力较小，但是EC具有低延迟、高宽带、访问距离短、地理分布灵活以及数据隐私保护等优点。

在实际通信场景中，不同的卸载任务对能耗和时延的要求各不相同，例如，AR、VR等应用任务对时延有严格要求；移动终端设备电量低时应对能耗问题更加关注。因此，如何平衡计算卸载中的能耗和时延是一个关键问题。

由于边缘服务器端通常电源充足，故在本文中主要对电量、内存、计算资源不足的移动终端设备进行研究。本文主要研究方向是通过优化算法寻找到一个最优任务卸载决策方案，使得任务卸载过程中，移动智能设备系统效用最大化。

1 网络模型

本文考虑搭建多用户单边缘服务器组成的网络模型，边缘计算卸载决策网络模型如图1所示，网络模型主要分为3个部分：边缘云、边缘中间层、移动终端设备。边缘云中包括一个边缘服务器和一个基站(base station，BS)，BS都有一定的存储容量和任务处理能力，边缘服务器部署在BS附近且位置固定，边缘服务器处理从移动终端设备传输来的计算密集型或时间敏感型任务。边缘中间层是边缘云与移动终端设备的中间枢纽，其中包括一个边缘网关和一个边缘调度器，边缘网关主要实现网络接入、数据采集与转发，边缘调度器根据边缘网关采集的数据得出卸载决策，并将卸载决策传输给边缘网关。

图1 边缘计算卸载决策网络模型

卸载决策过程简单描述为：边缘网关收集移动终端设备的待处理计算任务以及相关信息，然后将这些信息处理转发给边缘调度器。边缘调度器接收到信息后对任务卸载做出决策，再将卸载决策回传给边缘网关，边缘网关再传输给移动终端设备和边缘服务器。

假设当前场景中有K个移动终端设备，k∈{1，2，…，K}， 所有移动终端设备表示为L={L1，L2，…，LK} 集合，移动终端设备在固定时间段内只能产生一个计算任务，且计算任务不可分割。那么，在固定时间段内会产生K个待处理的计算任务，定义移动终端设备编号与计算任务编号相同。每个计算任务定义为一个四元组κk={Bk，Sk，Tmaxk，ak}，k∈{1，2，…，K}，Bk， B表示任务k数据量大小；Sk， MHz表示任务k需要的计算资源大小(机器周期数)；Tmaxk， s表示时延容忍度。ak∈{0，1} 表示对计算任务k的卸载决策，当ak=1表示计算任务k卸载到边缘服务器进行处理计算；ak=0表示计算任务k在本地的移动终端设备执行计算。本文中若任务k被选中卸载则全部卸载，即对每个计算任务作整体处理。为了便于分析，假设系统是一个准静态场景，即在一个卸载决策周期内，移动终端设备集合L保持不变。

2 计算模型

本节根据边缘计算中的计算卸载过程对问题进行抽象建模，最后得到计算卸载中移动终端设备的系统效用函数。

2.1 通信模型

在边缘计算卸载决策网络模型中，假设每个移动终端设备的上行传输链路均采用正交频分多址方法，因此，所有移动终端设备在上传卸载任务相关数据时，不会造成设备之间同频干扰。

假设应用于移动终端设备Lk的上行链路带宽为Wk， Hz，系统的上行链路总带宽为Wtotal=∑Kk=1Wk。 若移动终端设备以Pk的上传功率传输数据，根据香农公式可得计算任务k卸载时的上行传输速率

Rk=Wklog(1+PkHkσ2k)

(1)

式中：Hk表示Lk与BS之间的上行链路信道增益，σ2k表示Lk与BS之间上行链路噪声功率。

2.2 计算模型

2.2.1 本地计算模型

当ak=0， 计算任务k在本地执行，若flock表示Lk提供给计算任务k的计算资源大小，则计算任务k在Lk完成计算的时延可表示为

tlock=Skflock

(2)

式中：Sk表示任务k需要的计算资源大小(机器周期数)。

根据文献[8]，计算任务k在Lk执行计算的能耗可表示为

elock=γSk(flock)2

(3)

式中：能耗系数γ是与移动终端设备CPU芯片结构相关的常数，本文γ取值为10-17。若全部在Lk执行计算的任务总能耗表示为Eloc， 总时延表示为Tloc， 则有

Eloc=∑Kk=1(1-ak)elock

(4)

Tloc=∑Kk=1(1-ak)tlock

(5)

2.2.2 卸载计算模型

假设边缘服务器的计算资源足够大，且能同时处理多个计算任务。边缘服务器返回计算结果给移动终端设备的数据量较小且传输速率大，故在本文中忽略回传时延与能耗。

当ak=1， 计算任务k卸载到边缘服务器执行。若toffk表示任务k卸载到边缘服务器执行的时延，则toffk可表示为

toffk=tupk+twaitk

(6)

式中：tupk表示Lk上传计算任务k的传输时延；twaitk表示任务k卸载计算时，Lk等待时延。根据上传时间=数据量/速率可得tupk， 即

tupk=BkRk=BkWklog(1+PkHkσ2k)

(7)

式中：Bk表示任务k数据量大小；Rk是根据式(1)计算得到的传输速率。

当计算任务k卸载到边缘服务器后，边缘服务器为其分配的计算资源为fECk， 则twaitk可表示为

twaitk=SkfECk

(8)

本文边缘计算卸载决策系统的主要考虑移动终端设备端的能耗和时延，因此，任务卸载计算时，边缘服务器的计算能耗忽略。若eoffk表示任务k卸载到边缘服务器执行的能耗，则eoffk可表示为

eoffk=eupk+ewaitk

(9)

式中：eupk表示Lk上传计算任务k的传输能耗；ewaitk表示任务k卸载计算时，Lk空闲能耗。根据传输能耗=上传功率*时间可得eupk， 即

eupk=Pktupk=PkBkWklog(1+PkHkσ2k)

(10)

当计算任务k卸载到边缘服务器后，Lk空闲时功率表示为Pwaitk， 则ewaitk可表示为

ewaitk=Pwaitktwaitk=PwaitkSkfECk

(11)

若全部卸载到边缘服务器执行计算的任务总能耗表示为EEC， 总时延表示为TEC， 则有

EEC=∑Kk=1akeoffk=∑Kk=1ak(eupk+ewaitk)

(12)

TEC=∑Kk=1aktoffk=∑Kk=1ak(tupk+twaitk)

(13)

根据式(4)和式(12)可得移动终端设备的总能耗Etotal， 即

Etotal=Eloc+EEC=∑Kk=1(1-ak)elock+∑Kk=1ak(eupk+ewaitk)

(14)

根据式(5)和式(13)可得移动终端设备的总时延Ttotal， 即

Ttotal=Tloc+TEC=∑Kk=1(1-ak)tlock+∑Kk=1ak(tupk+twaitk)

(15)

2.3 优化问题制定

假设计算任务全部都在本地执行计算，总能耗设置为El、总时延设置为Tl。通过以上对计算模型的分析，移动终端设备在整个计算卸载过程中的系统效用函数SQ定义为

SQ=αEl-EtotalEl+βTl-TtotalTl

(16)

式中：系数α和β分别表示在进行卸载决策时，任务执行计算能耗和时延之间的权衡因子，α，β∈[0，1]，α+β=1。 若该系统应用于能耗不足的移动终端设备时，需适当调整α的值，且α>β；若该系统应用于时延敏感型任务时，需适当调整β的值，且α<β。 在本文中考虑时延和能耗同等重要，则α和β的取值均为0.5。在函数SQ中，若Etotal和Ttotal的值越小，则SQ的值越大，即在卸载过程中，移动终端设备系统效用越大；若Etotal和Ttotal的值越大，则SQ的值越小，即在卸载过程中，移动终端设备系统效用越小。因为，Etotal值越小，有利于延长移动智能设备的电池寿命；Ttotal值越小，有利于提高用户的服务体验质量，所以，为了实现计算卸载中移动终端设备系统效用最大化，将计算任务卸载的优化目标函数表示为

C1：ak∈{0，1}，∀k∈K

C2：fECk>0，∀k∈K

C3： ∑KkakfECk≤Fmax

C4：tlock≤Tmaxk，∀k∈K

C5：toffk≤Tmaxk，∀k∈K

C6：α，β∈[0，1]，α+β=1

(17)

其中，C1表示计算任务k的卸载决策；C2表示任务k得到的边缘服务器计算资源是一个大于0的正数，C3表示边缘服务器已被占用的计算资源之和不能超过自身最大计算资源Fmax； C4、C5都表示任务k的计算时延不能超过用户对时延的容忍度；C6中α和β是能耗和时延的权重因子。

3 算法设计

人工蜂群算法(artificial bee colony algorithm，ABC)是一种群智能算法，相比常见的遗传算法、蚁群算法等启发式算法，它的控制参数少、鲁棒性强、局部收敛性强、算法复杂度低、易于实现，但ABC易陷入局部最优解、开发能力弱[9，10]、收敛速度慢。为使ABC性能更好，每次优化更多变量，可以通过有效的变异和交叉组合来实现[11]。

差分进化算法(differential evolution，DE)是一种基于种群的全局随机搜索算法，具有较强的全局收敛性、稳定性、鲁棒性强等优点，但在算法执行后期收敛速度慢、可能会陷入局部最优解。

当研究基于群体智能或进化算法时，对于不同类型的问题，没有一种算法能够产生比所有其它算法都更好的解决方案[12]。本文提出优化问题P属于二进制0-1规划问题，而ABC和DE都是针对连续变量的算法，为了算法适用于本文的二进制优化问题，故采用离散二进制人工蜂群算法(BABC)和二进制差分进化算法(BDE)相结合来求解优化问题P。

3.1 二进制人工蜂群算法

BABC算法主要包括3种蜜蜂：雇佣蜂、跟随蜂、侦察蜂，每种蜜蜂负责一个阶段。在雇佣蜂阶段，每只雇佣蜂都试图改善自己的蜜源；在跟随蜂阶段，每只跟随蜂会根据蜜源的质量更新自己的蜜源；在侦察蜂阶段，如果跟随蜂不能改善蜜源，侦察蜂就会开始寻找新蜜源。

3.1.1 雇佣蜂阶段

雇佣蜂对蜜源位置更新，位置更新公式采用Kiran and Gündüz(2013)提出的逻辑运算公式

vi，j=Xi，j⊕ϑ(Xi，j⊕Xn，j)

(18)

其中，Xi，j表示是种群中的第i个蜜源，第j个问题维度的卸载决策，假设种群规模为N，i，n∈{1，2，…，N}，j={1，2，…，K}，i≠n；⊕表示异或运算，数值相同为0；相异为1；ϑ∈[0，1]。 表1中给出了式(18)的运算真值，对于状态1 (ϑ<0.5)， 如果输入位相同，则反转输出结果；否则输出值和输入位保持一致。

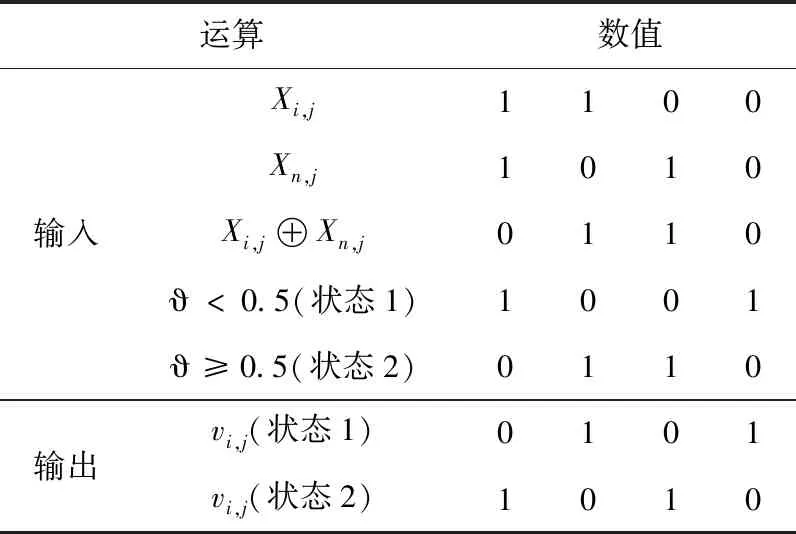
表1 逻辑运算真值

若新蜜源Vi={vi，1，vi，2，……，vi，K} 的适应度值大于Xi适应度值，采用贪婪选择的方式用Vi代替Xi， 否则保留Xi。

3.1.2 跟随蜂阶段

在跟随蜂阶段，采用轮盘赌方法选择跟随蜂。对于个体Xi， 若它的选择概率为pi， 产生一个r1∈[0，1] 的随机数，如果选择概率pi大于r1， 则根据式(18)重新产生一个新蜜源X_newi， 且采用雇佣蜂阶段相同的贪婪选择方法确定保留蜜源。

3.1.3 侦察蜂阶段

如果蜜源Xi经过trial次迭代没有找到更好的蜜源，且trial达到搜索阈值limit，则将蜜源Xi抛弃，与之对应的雇佣蜂转变为侦察蜂，侦察蜂随机产生一个新的蜜源代替Xi。

3.2 二进制差分进化算法

BDE算法与遗传算法相似，但比遗传算法易于实现，且具体操作不同，其主要包括3个步骤：变异、交叉、选择。

3.2.1 变 异

变异操作是根据变异公式把几个不同的个体融合成一个变异个体。Xingshi和Lin(2007)提出的二元突变方程

muti，j=Xr1，j⊙f⊗(Xr2，j⊗Xr3，j)

(19)

其中，Xr1，j、Xr2，j、Xr3，j是不同的3个个体，同一问题维度的卸载决策，且i≠r1≠r2≠r3，r1，r2，r3∈{1，2，…，N}，j={1，2，…，K}；f是变异算子，f∈[0，1]； 使用逻辑运算⊗(与)、⊙(或)可以使二进制字符串直接进化个体。

3.2.2 交 叉

定义r2∈[0，1] 的随机数，CR是交叉算子，CR∈[0，1]。 对于交叉向量cori的每个值都有如下交叉方法

cori，j={muti，j，ifr2≤CR，

Xi，j，otherwise.

(20)

其中，Xi，j表示第i个个体，第j个问题维度的卸载决策，j={1，2，…，K}。

3.2.3 选 择

采用贪婪选择的方式，在cori和Xi中选择适应度值较大的作为新的Xi。

3.3 binAD算法

提出基于BABC和BDE的新算法：binAD算法。binAD算法中将BABC和BDE相结合，并且对其中的变异操作和交叉操作进行改进。以下是binAD算法的详细介绍。

3.3.1 编码与初始种群

由于本文中的有K个待处理的计算任务，则种群的维度设为K，假设初始种群的规模为N，并采用式(21)生成初始种群。初始种群如图2所示，每一行表示一个个体，每个个体代表一个卸载决策向量Xi，i∈{1，2，……，N}， 则Xi，j表示第i个决策向量中第j个问题维度的卸载决策，j∈{1，2，…，K}

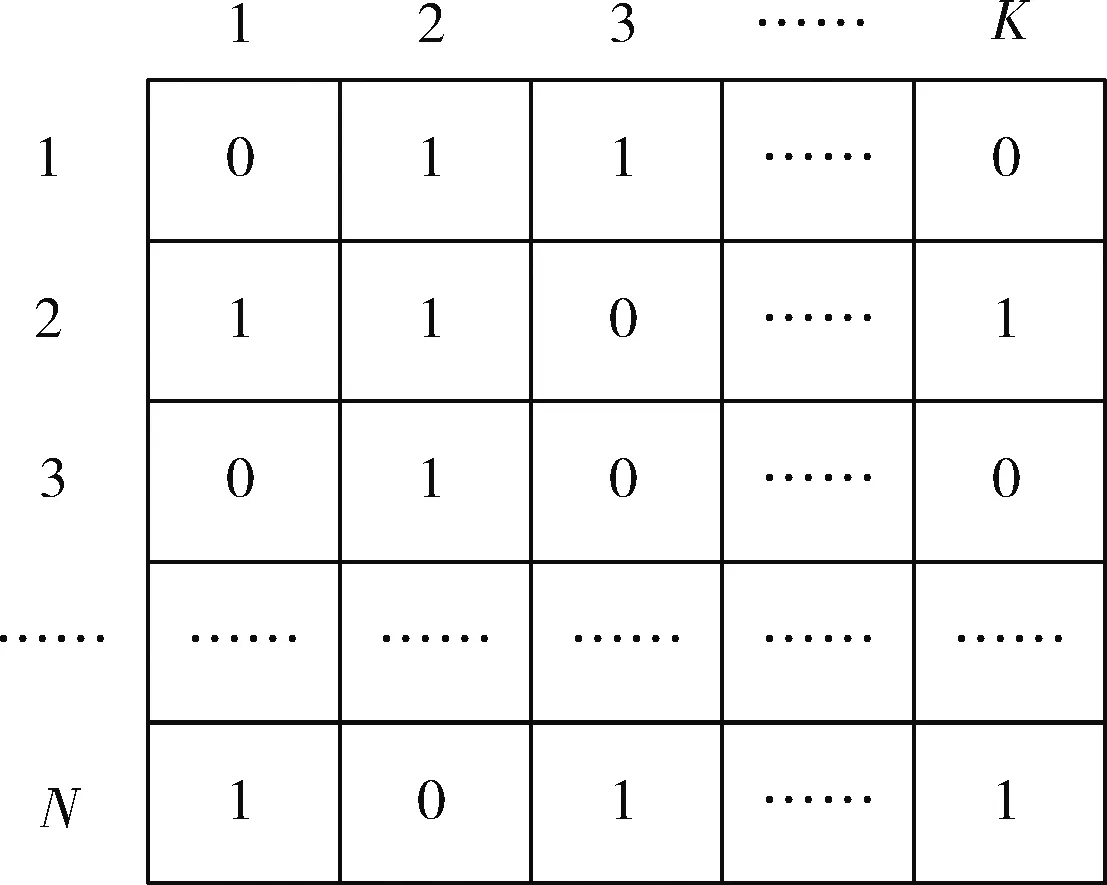
图2 初始种群

Xi，j={0，ifrand()<0.5，

1，otherwise.

(21)

3.3.2 适应度函数

由于本文主要研究方向是通过优化算法寻找到一个最优任务卸载决策方案，使得任务卸载过程中，移动智能设备系统效用最大化，所以根据式(16)将定义适应度函数为

Fitness(i)=SQ(i)

(22)

式(22)中取系统效用函数值直接作为算法中的适应度函数值，那么个体Xi的适应度函数值越大，则说明系统效用函数值越大，产生的能耗和时延，即该卸载决策越优。

3.3.3 引入最优个体的变异操作

在变异操作中引入最优个体，可以跳出局部最优解，向全局最优解靠近，且可以增大算法在解空间中的搜索范围。对式(19)改进得到如下变异公式

muti=f1⊗(Xbest⊕Xr1)⊙

f2⊗(Xr2⊗Xr3)

(23)

其中，Xbest表示全局最优个体；Xr1、Xr2、Xr3是不同于Xi的3个个体，且i≠r1≠r2≠r3，r1，r2，r3∈{1，2，…，N}；f1，f2∈[0，1]。

3.3.4 适应性交叉概率因子

BABC中的交叉概率对算法的性能影响很大，例如，收敛速度、搜索能力等，因此在本文中修改交叉概率为适应性交叉概率因子，如式(24)所示，以此提高算法的全局搜索能力

CR=0.6(iterMaxIt)2+0.3

(24)

其中，iter表示算法的当前迭代次数，MaxIt表示最大迭代次数。

binAD算法流程如图3所示。

图3 binAD算法流程

4 仿真实验与结果分析

在本节中，通过Matlab R2016a工具软件进行仿真和对比实验，并评估binAD算法的性能。

4.1 参数设置

本文中的相关仿真参数设置见表2。

表2 仿真参数设置

4.2 仿真实验与性能分析

为了验证算法的性能，将本文提出的binAD卸载决策与All-Local(计算任务全在本地执行)、Full-Off(计算任务全卸载到边缘服务器执行)、Random算法(随机卸载方法)、BABC算法(二进制人工蜂群算法)、IbinABC算法[13]的卸载决策进行比较，比较指标主要有：迭代次数、任务量、种群数量、能耗、时延、系统效用。

4.2.1 迭代次数的影响

设任务量为10，种群数量为100。如图4所示，展示了6种卸载决策在迭代次数从10增加到120，其系统效用的变化情况。当计算任务全部在本地执行(All-Local)时，系统效用全为0，这和系统效用函数的设计有关，同时也代表任务全部在本地执行是最不理想的卸载方案。当迭代次数小于等于30时，binAD算法对应的系统效用值有所波动，这是因为迭代次数较小，算法的搜索能力较弱，但当迭代次数大于30时，系统效用就趋于稳定，维持在0.32～0.35之间。总体来说，binAD算法在迭代次数对系统效用的影响中表现比BABC、Random、Full-Off、All-Local都好。

图4 迭代次数对系统效用的影响

4.2.2 种群数量的影响

本小节主要分析种群数量对时延、能耗、系统效用的影响。设置迭代次数为100，任务量为50。

种群数量对时延的影响如图5所示。从图5可知，All-Local的时延远远大于另外5种方案，这是因为本地移动终端设备自身条件受限，若执行大量任务会带来高时延。IbinABC、BABC和Random这3种算法的时延差距不太明显，但IbinABC相较于BABC和Random表现略好，且随着种群数量的增加，时延变化不大，比较平稳。Full-Off和binAD的时延明显低于另外4种方案，Full-Off时延较小是因为任务全部卸载到高性能的边缘服务计算，大大减少了任务计算时间，而binAD算法的时延和Full-Off接近，说明卸载决策偏向于将任务卸载，但是并不是完全卸载，是因为寻到最优的卸载方案。binAD算法的时延没有随着种群数量的增加而波动，说明算法的稳定好，全局搜索能力强。

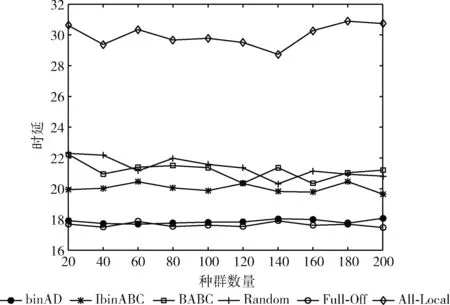
图5 种群数量对时延的影响

种群数量对能耗的影响如图6所示。从图中可以看出，All-Local的能耗较大，且远远高于另外5种方案，这是因为本地移动终端设备计算能力、内存等自身条件不足。相比binAD、IbinABC、BABC、Random算法，Full-Off的能耗也较高，因为卸载的任务数据量太大，导致上传数据的能耗增大。种群数量的变化对Random的能耗影响不大，随机算法具有盲目性且没有收敛性。当种群数量小于120时，BABC的能耗有下降趋势，但当种群数量大于120时，最优解的搜索范围增加，反而使BABC找寻最优解的能力降低。binAD和IbinABC随着种群数量的增加，能耗都明显低于另外4种方案，且表现稳定，说明这两个算法的全局搜索能力和稳定性都较好，只是IbinABC在种群数量大于160时，能耗的波动较大。

图6 种群数量对能耗的影响

种群数量对系统效用的影响如图7所示。由于系统效用函数的设计，任务全部在本地执行计算方案的系统效用依然为0。随着种群数量的增加，BABC和Random的系统效用都呈上升趋势，且差距不大，但是相较于binAD、IbinABC和Full-Off系统效用表现不好。IbinABC和Full-Off的系统效用虽然优于All-Local、BABC和Random，但binAD算法的系统效用表现更好，且明显高于另外5种卸载方案。当种群数量大于120时，binAD算法表现非常稳定，没有随着种群数量的增大而波动。综上，binAD算法算法的稳定好，且全局搜索能力强，全局寻优能力强。

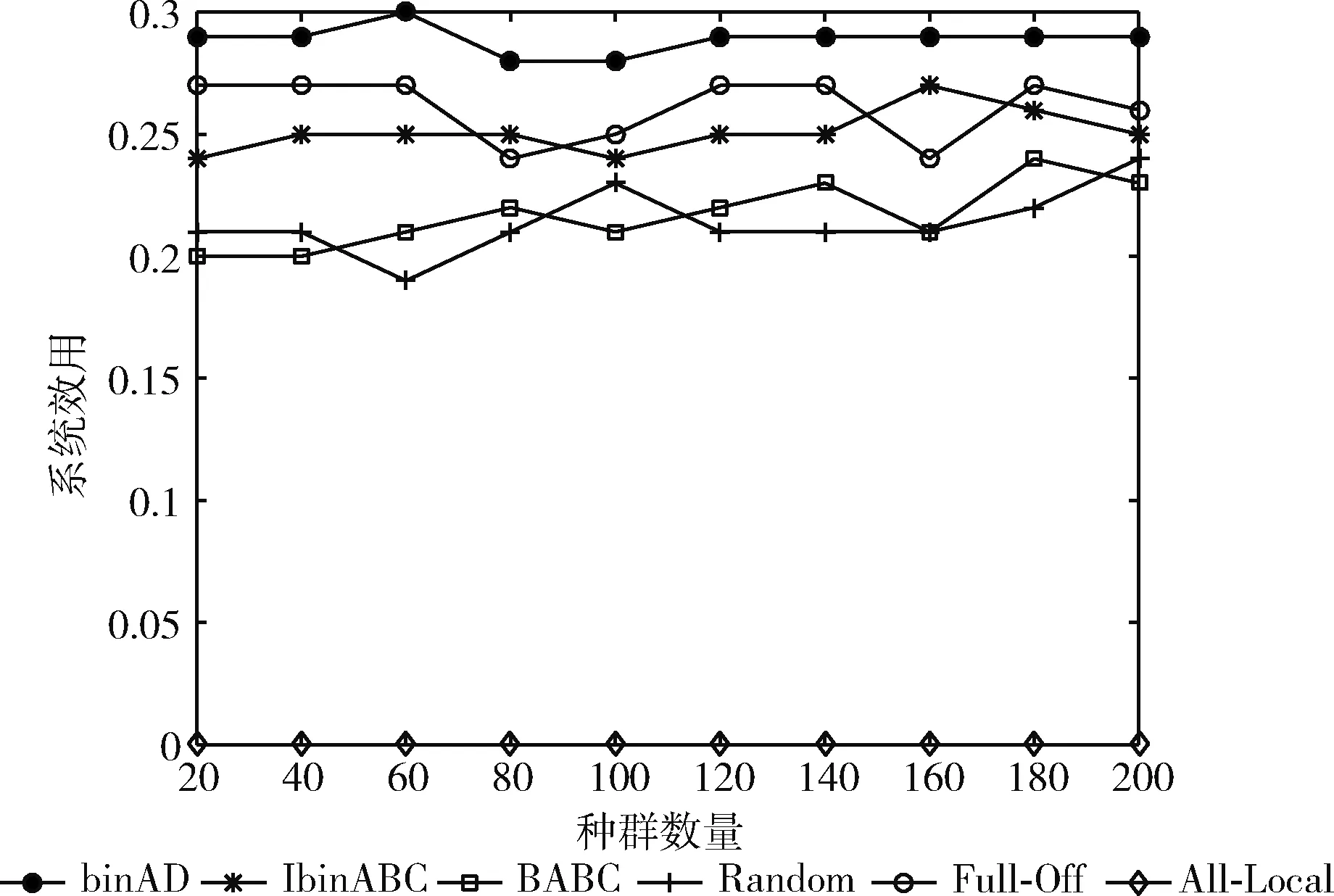
图7 种群数量对系统效用的影响

4.2.3 任务量的影响

本小节主要分析任务量对时延、能耗、系统效用的影响。设置迭代次数为100，种群数量为50。

从图8任务量对时延的影响可以看出，随着任务量的增加，各种方法生成的计算卸载决策在时延上都随之增大。由于移动终端设备的计算能力有限，随着任务量的增加，移动终端设备的负载增加，所以All-Local的时延明显高于另外5种卸载方案。在任务量小于40时，binAD、IbinABC、BABC、Random、Full-Off的时延差距不大，但当任务量大于40时，binAD和Full-Off的时延明显低于IbinABC、BABC、Random。binAD算法的时延和Full-Off接近，这里再次说明binAD卸载决策偏向于将任务卸载，但是并不是完全卸载，是因为寻到最优的卸载方案。

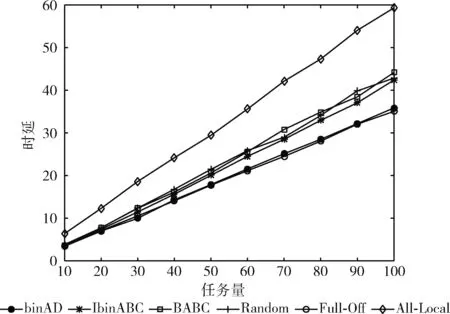
图8 任务量对时延的影响

从图9任务量对能耗的影响可以看出，随着任务量的增加，各种方法生成的计算卸载决策在能耗上都随之增大。其中，All-Local的能耗明显高于另外5种卸载方案。而binAD、IbinABC、BABC、Random、Full-Off这5种卸载的方案的能耗差距不明显。随着任务量的增加，binAD算法在能耗方面表现一般。

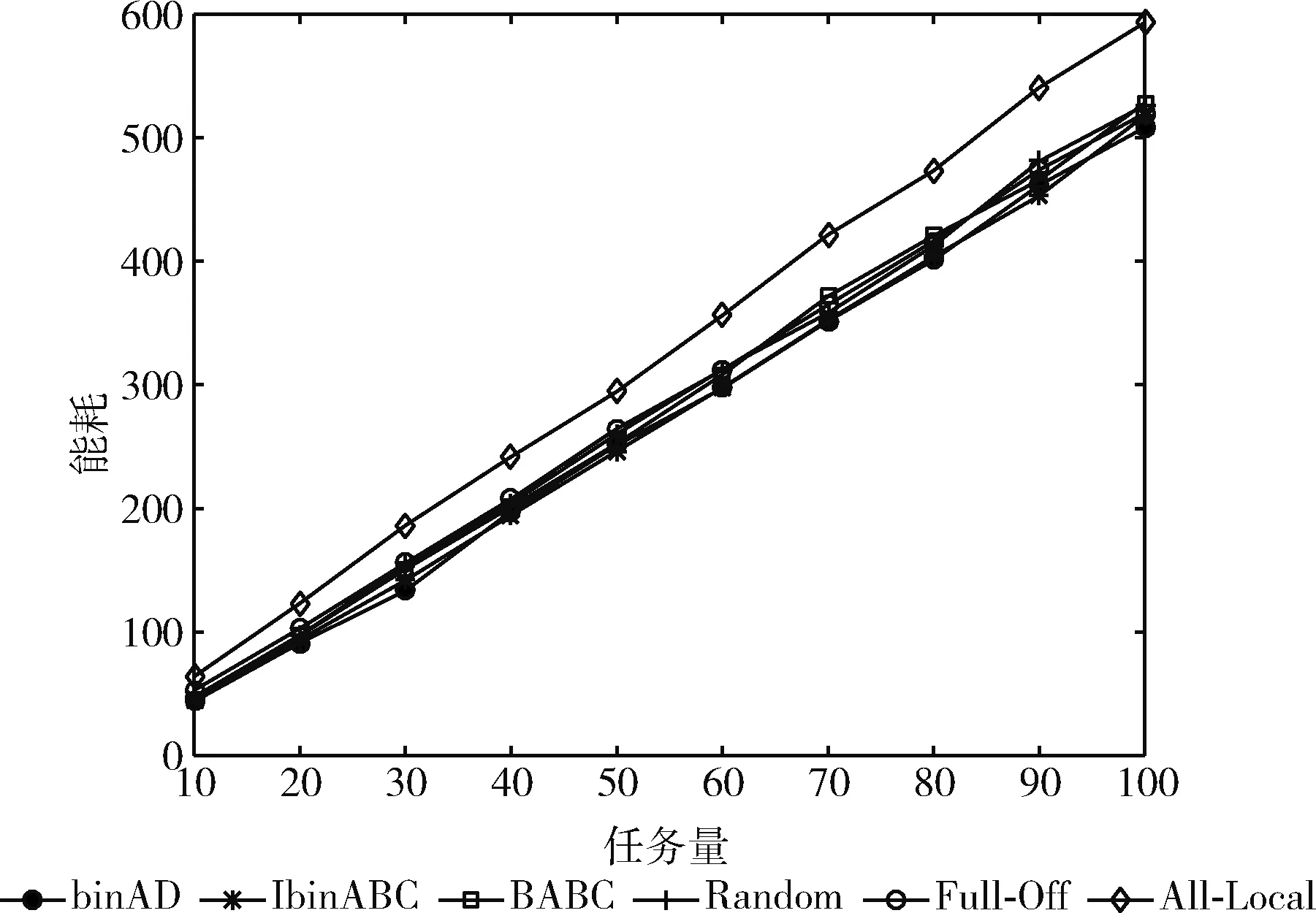
图9 任务量对能耗的影响

如图10任务量对系统效用的影响所示。由图可知，除了All-Local其余5种卸载方案的系统效用都有降低趋势，这是因为各种方法生成的计算卸载决策在时延和能耗都随任务量的增加而增大，则系统效用函数值随之降低。其中，binAD算法在任务量大于50时，其系统效用表现平稳，说明该算法在大量计算任务情况下，全局搜索能力强。binAD算法虽然在图9能耗方面表现一般，但是在图8时延方面表现不错，因此binAD算法在系统效用优于其它5种卸载方案。

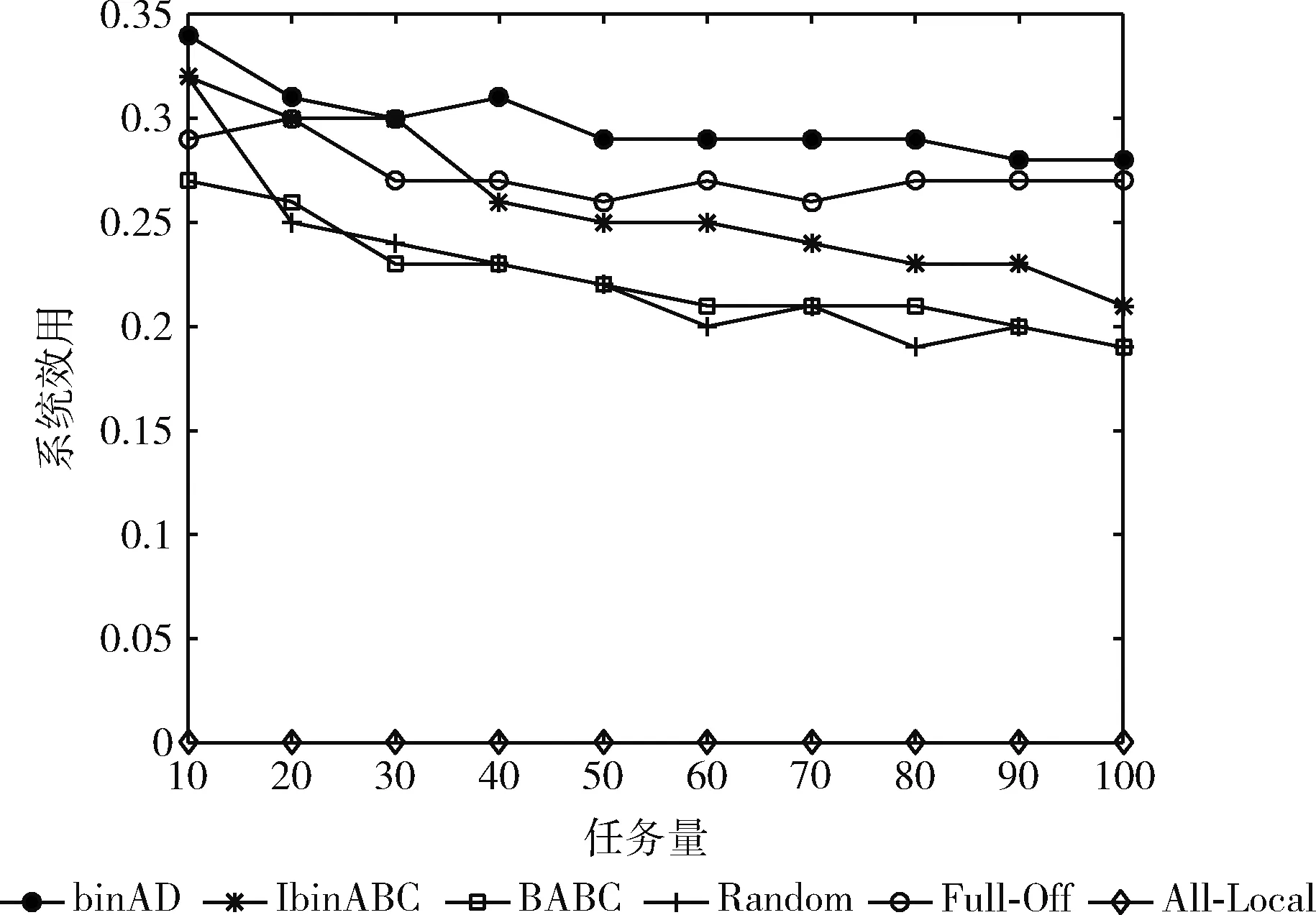
图10 任务量对系统效用的影响

5 结束语

本文采用binAD算法解决边缘计算中的卸载决策问题。以最大化移动终端设备系统效用为目标，制定边缘计算卸载决策优化问题。为了克服BABC和BDE两种算法的缺点，将二者相结合，并改进其中的变异操作和交叉概率因子，得到binAD算法，该算法扩大了可行解范围、全局搜索能力强、稳定性好。binAD算法在时延和系统效用方面可以取得较好的结果，但在能耗方面表现一般。由于本文提出的binAD算法在能耗方面表现一般，未来可在能耗方面继续研究，实现更优的边缘计算卸载决策。